Diseño de pieza con materiales compuestos
La adhesión entre la fibra y la matriz es un aspecto clave en las prestaciones mecánicas de un material compuesto. Si no hay una buena adhesión en la interfase fibra-matriz, cada uno de los materiales se comportará mecánicamente de forma individual; así, si atendemos a la figura 1 ante un esfuerzo de baja intensidad σ1 la fibra se deformará ε1f y la matriz lo hará en una cantidad mayor (ε1m). En estas condiciones, como la deformación de cada una de los materiales es diferente, se produce una separación física entre la fibra y la matriz dando lugar a la fractura del compuesto. Esta situación, lógicamente no es deseable cuando se trabaja con este tipo de materiales ya que no se aprovecha la sinergia en la combinación de los diferentes componentes. Sería posible moldear la pieza con un material compuesto de estas características pero las propiedades mecánicas no serían las deseadas.
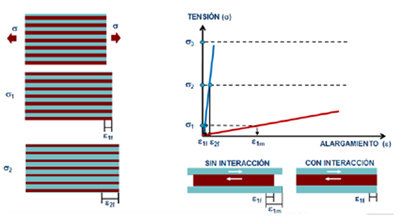
Por el contrario, cuando se produce una buena interacción en la interfase fibra-matriz, es decir, existe buena adhesión entre los componentes, la fibra se deforma en una cantidad equivalente a lo que indica su diagrama de tracción (ε1f) y la matriz, al estar completamente adherida a la fibra de refuerzo, lo hará en la misma extensión (ε1f), de tal manera que en estas condiciones, la matriz prácticamente no trabaja desde el punto de vista mecánico y es solamente la fibra la que actúa como elemento resistente. El material compuesto ha actuado de forma sinérgica entre sus constituyentes. Este condicionante es básico para poner una pieza de material compuesto en funcionamiento.
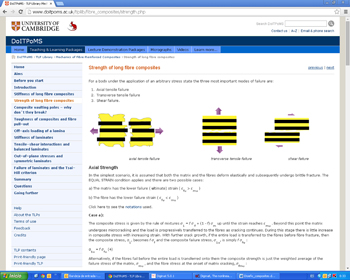
La curva tensión-deformación del material compuesto en realidad se situará entre las del refuerzo y la matriz, en función de la fracción volumétrica de ambos componentes. Por lo tanto, cuando un material compuesto es sometido a una carga excesiva en funcionamiento, el fallo puede producirse bien porque fallen los constituyentes o bien porque falle su interfase. De esta manera, una vía para determinar la resistencia de un composite exige conocer el estado de tensiones de (figura 2):
a) Las fibras, que pueden fallar a tracción o a compresión. Normalmente no presentan comportamiento plástico, por lo que al alcanzar el límite elástico rompe la fibra, redistribuyéndose las cargas entre las que todavía no han fallado.
b) La matriz, que falla principalmente por micro-fisuración que se extiende debido a cargas de tracción, compresión y cizalla.
c) La interfase fibra-matriz. Debido a la diferencia de los esfuerzos cortantes entre fibra y matriz, una fase se desplaza con respecto a la otra. Los resultados de esta pérdida de adhesión se han explicado previamente.
d) La interfase lámina-lámina. Cuando distintas capas se apilan para intentar contrarrestar la anisotropía del material, el fallo puede producirse en la zona de unión entre las distintas láminas. Si esto sucede, no pueden distribuirse las cargas entre ellas.
Volviendo al caso de una lámina unidireccional, ante determinada carga que se incrementa sucesivamente y suponiendo una buena adhesión entre fibra y matriz, ¿Qué falla primero? ¿El refuerzo (cuyo módulo elástico es superior por definición) o la matriz? Evidentemente esto depende de las propiedades de dichos constituyentes y de la fracción volumétrica de cada uno de ellos en el laminado. En concreto, deberá ponerse atención a su alargamiento a rotura. Puede darse el caso de matrices con superior alargamiento a rotura que algunos refuerzos. Así, es posible encontrar resinas de tipo epoxi que pueden deformarse hasta un 6% antes de producirse la extensión de las microfisuraciones hasta observar la rotura de dicha fase, mientras que tanto la fibra de vidrio como la de carbono no suelen permitir más de un 2% (sobre todo estas últimas).
Cuando el alargamiento a rotura de la matriz es inferior al del refuerzo, al tenerse una carga tal que se produce dicha deformación, la matriz se agrietará y la carga tendrá que ser transferida completamente al refuerzo. Si, llegado a este punto, la tensión aplicada es todavía inferior al producto de la resistencia a tracción del refuerzo por su fracción volumétrica, el composite seguirá soportando la carga hasta que no se cumpla la anterior condición, momento en el que fallará a tracción (figura 2).
Si, por el contrario, el alargamiento a rotura de la matriz es superior al del refuerzo, a medida que vayan fallando las fibras, la carga se transferirá a la matriz, quien presenta de forma general una resistencia a tracción inferior a la del refuerzo, por lo que también fallará de forma súbita.
En la práctica, es difícil ver el caso de composites formados únicamente por láminas unidireccionales. De uso frecuente son o bien los apilamientos multidireccionales o la presencia de refuerzos en los que las fibras se orientan de forma aleatoria, si bien estos últimos permiten un nivel de empaquetamiento de fibras muy reducido. En este tipo de materiales compuestos. ¿Cómo predecir el fallo? Por un lado es posible atender a la teoría clásica de laminados, repartir la tensión entre todos ellos e ir eliminando láminas a medida que fallen y redistribuyendo de nuevo la tensión entre las restantes. Sin embargo, la estrategia más usada es confiar en criterios de fallo polinomiales (tipo Tsai-Wu) en los que a partir de las propiedades del material compuesto es posible localizar las zonas de la pieza susceptibles de rotura ante un determinado esfuerzo.
Llegados a este punto, el lector puede suponer que el laboratorio físico – mecánico debe ponerse en marcha para caracterizar las propiedades de un buen número de distintos laminados que componen la pieza y así poder utilizar herramientas computacionales basadas en elementos finitos donde poder analizar las zonas de la pieza en las que el criterio de fallo escogido predice la ruptura de la misma. Sin embargo, es posible la reducción del esfuerzo de caracterización con el empleo de nuevas herramientas que son capaces de predecir el comportamiento del laminado (independientemente de la orientación de las fibras y su fracción volumétrica) con un alto nivel de precisión a partir de un número muy limitado de caracterizaciones del material compuesto.
En Aimplas disponemos tanto de las herramientas computacionales como de los laboratorios necesarios para el desarrollo de su proyecto concreto con materiales compuestos, optimizando el diseño de la pieza y su composición, de tal forma que sea posible sustituir materiales tradicionales por composites de reducido peso y coste.