Empleo de criterios de fractura dúctil para predecir el fallo en el conformado plástico de chapas
Área de Ingeniería de los Procesos de Fabricación.Departamento de Ingeniería Mecánica y de los Materiales. Universidad de Sevilla.15/02/2004
En el presente trabajo se examina la capacidad de varios criterios de fractura dúctil, ampliamente usados en la práctica, para predecir y reproducir el proceso físico del fallo en procesos de conformado plástico de chapas. Así mismo se propone y se analiza un criterio alternativo de fallo, el cual surge de modificar el conocido criterio de Freudenthal para incluir el efecto de la tensión hidrostática en el proceso de fractura. Para centrar el estudio se ha realizado un modelo de Elementos Finitos (EF) del proceso de embutición de chapa axilsimétrico, empleando el paquete comercial de elementos finitos ANSYS. Sobre este proceso, se han implementado los diferentes criterios de fractura dúctil, analizándose el lugar donde estos predicen en fallo, el estado de tensiones y deformaciones en dicha zona, la Relación Límite de Embutición (RLE), etc. Los resultados de las simulaciones realizadas se han comparado con los resultados experimentales obtenidos por Takuda et al. [1] para chapas de diferentes aceros.
Criterios de fractura dúctil de uso extendido
En este trabajo se van a explorar cuatro criterios de fractura dúctil ampliamente conocidos: los clásicos criterios de Cockcroft y Latham [3] y Brozzo et al. [4], incluidos en la primera categoría, y los criterios de Oyane et al. [5] y Chaouadi et al.[6], pertenecientes al segundo grupo descrito. Estos criterios requieren conocer la historia de carga y de deformación que sufre el material durante todo el proceso, pudiendo expresarse en forma integral de la siguiente forma:
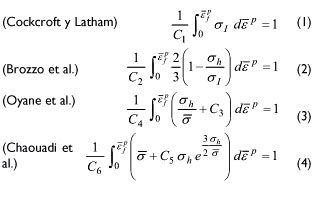
Alternativamente a los criterios anteriores presentados, se va a proponer en este trabajo un nuevo criterio semi-empírico basado en una modificación del clásico criterio Freudenthal. El criterio de Freudenthal establece que la fractura se inicia cuando el trabajo plástico por unidad de volumen en un determinado punto del material alcanza un cierto valor crítico. Dicho modelo ha sido empleado con éxito para predecir el fallo en procesos de deformación plástica global [5]. No obstante, cuando se aplica a procesos de conformado de chapa su comportamiento no ha sido nada satisfactorio [2]. Entre las causas argumentadas para explicar este hecho, la aceptada es que el criterio original de Freudenthal no incluye el efecto de la tensión hidrostática en el proceso de fractura dúctil. Es bien conocido que mientras que la tensión hidrostática no tiene una repercusión apreciable en el proceso de plastificación, durante la fractura dúctil es todo lo contrario, favoreciendo decisivamente la fase de crecimiento de cavidades y contribuyendo con ello a acelerar el proceso fractura. Para tener en cuenta este efecto, se propone aquí incluir en la expresión del trabajo plástico un término extra que dependa de la tensión hidrostática. La forma más simple que se plantea seguidamente es una dependencia lineal, quedando el nuevo criterio de la forma:
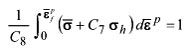
(5)
donde C7 y C8 y son constantes del material. En lo que sigue, y por simplicidad, nos referiremos a dicho criterio como criterio del Trabajo Plástico Modificado (criterio TPM).
Modelado y simulación numérica del proceso de embutición
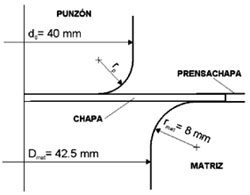
El modelo de EF desarrollado realiza una descripción Lagrangiana, empleando una formulación con grandes deformaciones dada la fuerte no linealidad del problema, debida principalmente al comportamiento plástico del material y al contacto entre los diferentes elementos. La matriz, el punzón y el prensa-chapa se han considerado elementos rígidos. Para la chapa metálica se ha supuesto un comportamiento elasto-plástico con endurecimiento por deformación isotrópico. En primera aproximación se ha empleado un modelo de plasticidad asociativa isótropo e independiente de la velocidad de deformación, tomando el criterio de von Mises como criterio de fluencia. Esta aproximación es apropiada siempre que la anisotropía característica de la chapa no sea muy elevada.
La Figura 2 muestra la malla empleada en una configuración genérica. Los elementos usados han sido cuadriláteros de 8 nodos (PLANE82). Dependiendo el espesor de la chapa se han empleado 4 capas de elementos para chapas de espesores inferiores a 1 mm y 5 capas para espesores de 1 mm. Las superficies en contacto se han mallado usando los pares de elementos CONTA172 y TARGE169 de ANSYS. Se supone que la fricción entre las superficies sigue un modelo de Coulomb, con un coeficiente de fricción de 0.1. La fuerza inicial ejercida por el prensa-chapa sobre la chapa se ha obtenido a partir de la conocida expresión de Siebel. Por último, se ha considerado el proceso de embutición como un problema cuasi-estático, resolviéndose de manera incremental. El criterio de convergencia establecido supone que ésta se alcanza cuando el módulo (norma Euclídea) del vector de los residuos es inferior a un 0.5% del módulo del vector de cargas exteriores.
Comparación experimental de las predicciones de fallo. Discusión
Como se ha mencionado en el apartado anterior, las simulaciones realizadas intentan reproducir los ensayos de embutición de Takuda et al. [1]. Dichos ensayos se efectuaron empleando tres materiales distintos: chapa de acero inoxidable 430 con espesor de 0.78 mm (Material 1), chapa de acero de alta resistencia con espesor de 1 mm (Material 2) y chapa de acero cincado de 0.7 mm de espesor (Material 3). Las propiedades mecánicas de estos materiales se muestran en la Tabla 1. Como se puede observar en dicha tabla, el coeficiente de anisotropía normal en las distintas chapas es suficientemente próximo a la unidad como para considerar aceptable, desde un punto vista ingenieril, la hipótesis de comportamiento isótropo en las simulaciones de EF.
| Material | E (GPa) | su (MPa) | K (MPa) | n | r | e I,f (uniaxial) | e I,f ( def.plana) |
| 1 | 210 | 488 | 829 | 0.20 | 0.81 | 0.595 | 0.336 |
| 2 | 672 | 1020 | 0.14 | 0.91 | 0.634 | 0.285 | |
| 3 | 748 | 858 | 0.03 | 0.87 | 0.303 | 0.130 |
Para cada uno de los materiales comentados, se ha simulado la embutición de chapas circulares de diferentes diámetros iniciales, evaluando el fallo o no de la misma a partir de los criterios de fractura descritos anteriormente. La Tabla 2 muestra las constantes del material para los distintos criterios. Dichas constantes se han calculado a partir de los dos valores de eI,f de la Tabla 1, los cuales representan la deformación principal máxima de fractura obtenida respectivamente para un ensayo de tracción uniaxial pura y para un ensayo de tracción bajo condiciones de deformación plana. Por tanto, para determinar las constantes basta con particularizar cada uno de los criterios anteriores para las condiciones de ambos ensayos y despejar sus valores. En el caso de que el criterio tenga una única constante a determinar, el valor de dicha constante se corresponde con el valor medio de los obtenidos al particularizar el criterio para los dos ensayos.
| C1 (MPa) | C2 | C3 | C4 | C5 | C6(MPa) | C7 | C8 (MPa) | |
| Material 1 | 313.3 | 0.556 | 0.124 | 0.272 | 1.480 | 670.87 | 32.69 | 4407.54 |
| Material 2 | 411.6 | 0.536 | -0.070 | 0.167 | 5.240 | 2065.65 | -8.78 | -1026.06 |
| Material 3 | 189.9 | 0.252 | -0.094 | 0.073 | 4.430 | 836.24 | -9.67 | -541.13 |
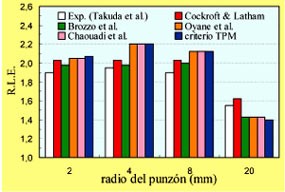
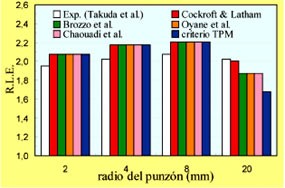
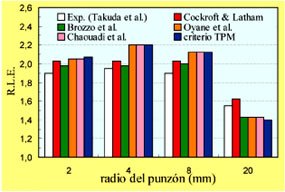
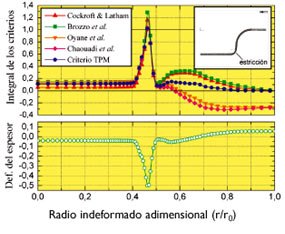
Una vez analizada la capacidad predictiva de los modelos propuestos, la pregunta que surge de manera natural es si dichos criterios reproducen adecuadamente el proceso físico de fallo de acuerdo con la evidencia experimental. En los ensayos de Takuda et al. el fallo se produce en la zona del radio del punzón, para todas las situaciones y materiales empleados. Se observa que inicialmente la deformación se concentra en una banda muy estrecha del orden del espesor de la chapa, lo que se conoce como estricción localizada, y que finalmente se produce la fractura del material en dicha zona. Este hecho está en perfecto acuerdo con las predicciones obtenidas por todos los modelos analizados para los materiales más dúctiles, es decir, Material 1 y Material 2.
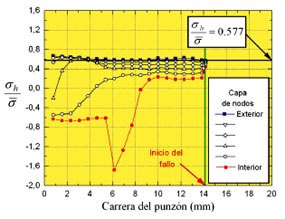
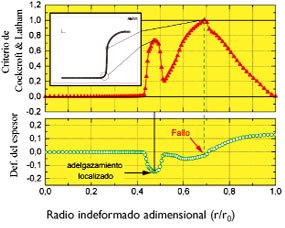
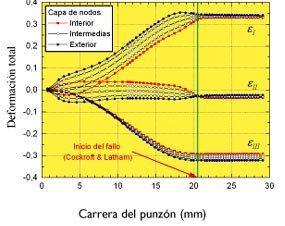
Conclusiones
- Se ha analizado la capacidad para predecir el fallo en productos de chapa conformada de diferentes criterios de fractura dúctil. Las predicciones obtenidas se ajustan muy razonablemente a los resultados experimentales obtenidos por Takuda et al. para diferentes aceros.
- Estos criterios predicen el fallo en la zona de estricción localizada cuando el estado local de tensiones alcanza las condiciones de Deformación Plana, de acuerdo con la evidencia experimental.
- Para el material menos dúctil los criterios de Cockcroft y Latham y de Brozzo et al. tienen una ligera tendencia a predecir el fallo en zonas de cortante puro (espesor constante), hecho experimentalmente observado también en algunas embuticiones realizadas con aleaciones de aluminio.
- El criterio de Trabajo Plástico Modificado propuesto muestra resultados en buena concordancia con resultados experimentales y el resto de criterios analizados.
Referencias
[2] Takuda H., Mori K. and Hatta N. (1999) “The application of some criteria for ductile fracture to the prediction of the forming limit of sheet metals” J. Mater. Proc. Tech. 95, 116-121.
[3] Cockcroft M. G. and Latham D. J., Ductility and the workability of metals, J. Inst. Metals 96, 33, 1968.
[4] Brozzo P., De Luca B. and Rendina R., A New Method for the Prediction of the Formability Limits of Plastic Sheets, Proc 7th Biennial Congress of the IDDRG, 1972.
[5] Oyane M., Sato T., Okimoto K. and Shima S., Criteria for Ductile Fracture and Their Application, J. Mech. Working Tech., 4, 66-81, 1980.
[6] Chaouadi R., De Meester P. and Vandermeulen W., Damage work as ductile fracture criterion, Int. Journal of Fracture 66, 155-164, 1994.
[7] Clift S. E., Hartley P., Sturges C. E. N. and Rowe G. W., Fracture Prediction in Plastic Deformation Processes, Int. J. Mech. Sci., 32, 1-17, 1990.
[8] ANSYS User’s guide, Release 5.5, ANSYS Inc., 1998.
[9] Forming Limit Diagram: Concepts, Methods and Application, Edited by R. H. Wagoner, K. S. Chan and S. P. Keeler, The Minerals, Metals & Materials Society, Warrendale, Pennsylvania, 1989.


























