Cómo reducir el consumo de combustible y emisiones de los aviones, ‘Premio trabajo fin de máster del COIAE 2019’

En los últimos años, los principales fabricantes del sector han tratado de diseñar aeronaves que cumplieran con las distintas necesidades de sus clientes (ej.: mayor número de pasajeros, mayores distancias etc.). En concreto, casi todas las soluciones propuestas pasaban por un punto muy importante, que es la reducción del consumo de queroseno, el cual constituye en torno a una cuarta parte de los gastos operativos de cada vuelo [1]. Y esta reducción del consumo se encuentra intrínsicamente relacionada con la reducción de la resistencia total de la aeronave.

En este aspecto, hay dos fuentes importantes de resistencia: la primera, y más evidente, la resistencia de forma, relacionado con el aspecto aerodinámico de la aeronave, y contribución muy optimizada a lo largo de la historia como se puede comprobar en el hecho de que la mayoría de los aviones modernos (ej.: A320neo, 737-MAX) son optimizaciones de sus predecesores, pero que a grandes rasgos son muy similares en forma; y la segunda, y menos estudiada, la resistencia viscosa, debida a las interacciones de las partículas del fluido (aire) con las superficies sólidas (aeronave). Esta última contribución, también conocida como fricción de la piel, puede constituir hasta un 40-50% de la resistencia total de la aeronave en condiciones de crucero [2] y con el incremento de las velocidades de vuelo, la contribución de la fricción de la piel es cada vez mayor.

Estudios recientes de la comunidad científica, y apoyados por la industria, se enfocan en diseñar estrategias para reducir la pérdida de energía y momento por la fricción de la piel a través del control de la turbulencia [3]. Por ello, el estudio del control de la turbulencia de pared es de gran importancia para entender lo que sucede en la capa límite de las alas de nuestras aeronaves.

Una de las técnicas más comunes para el control de la turbulencia de pared es la llamada control por oposición, consistente en realizar actuaciones de succión/expulsión sobre la pared, de manera opuesta a las fluctuaciones verticales de la velocidad cerca de la misma [4], [5]. Además, la influencia de nuevos campos como son el uso de redes neuronales [6] o el deep-learning [7] para investigar estas estrategias de control suponen un gran paso adelante en estos estudios.

En este entorno se define el marco de esta tesis de máster, que consiste en la realización de un estudio estadístico preliminar que evalúe el efecto que una determinada acción tiene sobre un determinado estado del flujo en la fricción de pared de un canal turbulento. Para ello, realizamos un análisis de Monte Carlo, con un gran número de episodios (16.500 aprox.) que evalúan el efecto de distintas acciones sobre el flujo. Esto, en última instancia, permitirá generar una estrategia de control estadística que nos indicará cual es la acción óptima que realizar para cada estado.

Para ello, diferentes variables del flujo como la presión y los esfuerzos de cizalladura en la pared fueron analizadas a través de un experimento numérico de un flujo de canal turbulento, por medio de simulaciones numéricas directas (DNS). Además, estas simulaciones fueron llevadas a cabo por medio de tarjetas gráficas (GPUs), las cuales permiten paralelizar el cómputo del estado del flujo y reducir los tiempos de cálculo. Así, es posible realizar un mayor número de simulaciones para un mismo período de tiempo, aumentando el grado de confianza de nuestros resultados estadísticos.

El uso del problema canónico de los flujos de canal para estudiar la capa turbulenta de sus paredes permite extrapolar los resultados obtenidos a lo que ocurre en las alas de las aeronaves. Además, el uso de canales mínimos como el propuesto por Jiménez y Moin [8], permite definir una primera base sobre la que evaluar el impacto de nuestras actuaciones con un tiempo computacional asequible.

Definimos las principales características de nuestro canal con dimensiones L_x=ph, L_y=2h, L_z=ph/2, donde h es la semi-altura del canal; un número de Reynolds de fricción Re_t=(ut h)/ν=165, donde ut es la velocidad de fricción y ν la viscosidad cinemática; periodicidad en las condiciones de contorno en las dimensiones transversales y longitudinales del flujo (X y Z), y un flujo de masa constante con un número de Reynolds de 5600. Un ejemplo de la geometría se puede observar en la ilustración 1. Con un canal de estas características es importante reseñar que es posible obtener una buena representación de las estructuras y la dinámica del flujo de la zona cercana a la pared.

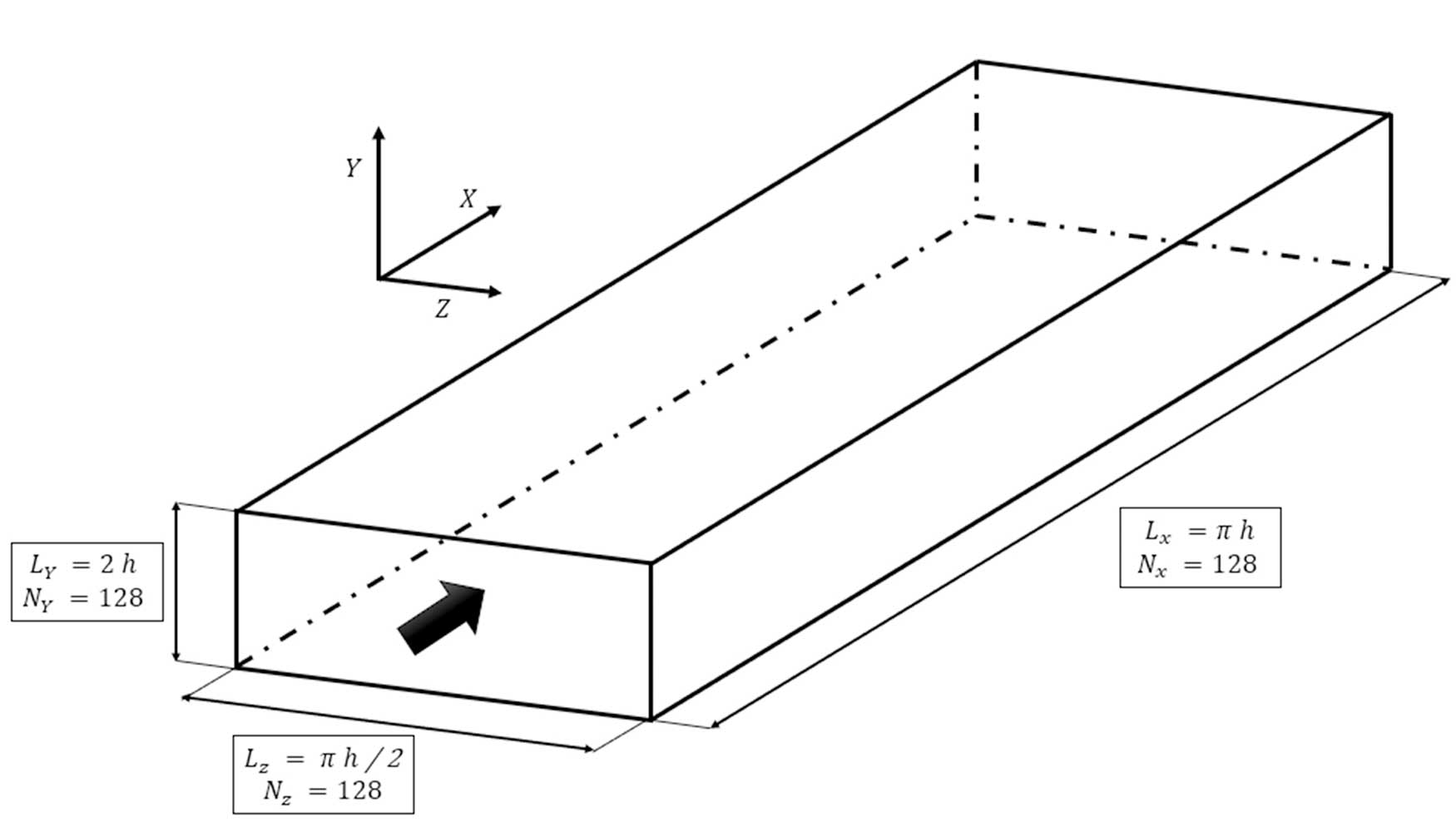
Las actuaciones o forzados que se llevarán a cabo sobre el flujo consistirán en la implantación de fuerzas volumétricas en la pared inferior del canal que presentan una distribución espacial gaussiana y que estarán activas durante ciertos periodos de tiempo en cada simulación. Esto nos deja una serie de variables con las que construir los casos bajo estudio: L_f, la longitud característica del forzado; T_f, el tiempo característico del forzado; y F₀, la intensidad del forzado. Si normalizamos estas variables en términos de unidades de pared (ej.: y⁺=y·ν/u_t, t+=t·(u_t²)/ν, …), definimos los siguientes casos de forzado:

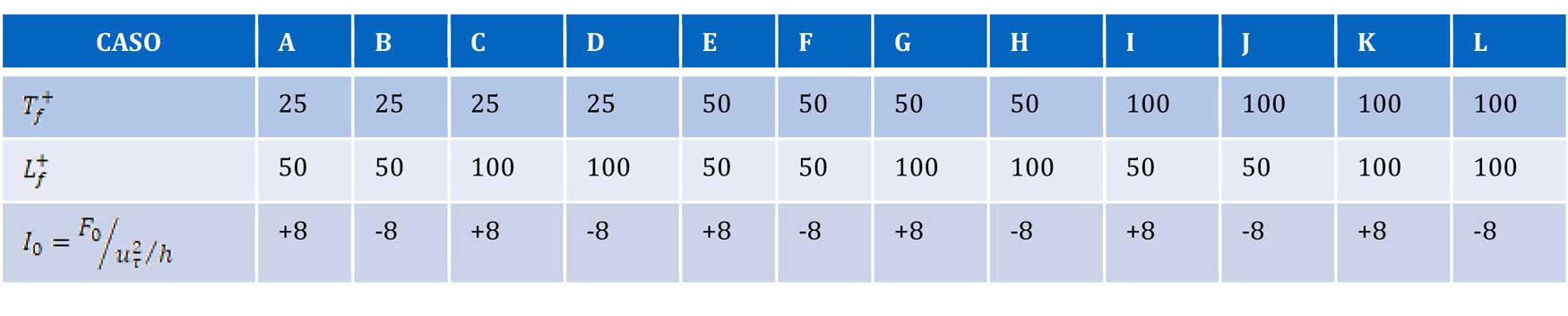
Es importante reseñar que los forzados con una intensidad positiva implican que la dirección de la fuerza es hacia el interior del canal (es decir, como si ‘soplásemos’ desde la pared inferior del canal), mientras que los forzados de intensidad negativa son aquellos en los que la fuerza se ejerce en dirección hacia la pared inferior del canal (es decir, como si ‘succionásemos’ desde la misma).

Para evaluar todos estos forzados, se propuso analizar el flujo de canal bajo las mismas condiciones iniciales, de tal manera que cada episodio partiese de un mismo estado, e implicaba 13 simulaciones: 1 de ellas sin forzado y las otras 12 con cada uno de los casos expuestos anteriormente. De esta manera se podía evaluar cada episodio bajo las mismas condiciones y ver cuál era el efecto de cada uno de ellos. Los periodos de cada simulación eran de t_episodio=3·h/u_t, lo cual permitía al flujo estabilizarse tras el forzado (ver ilustración 2).

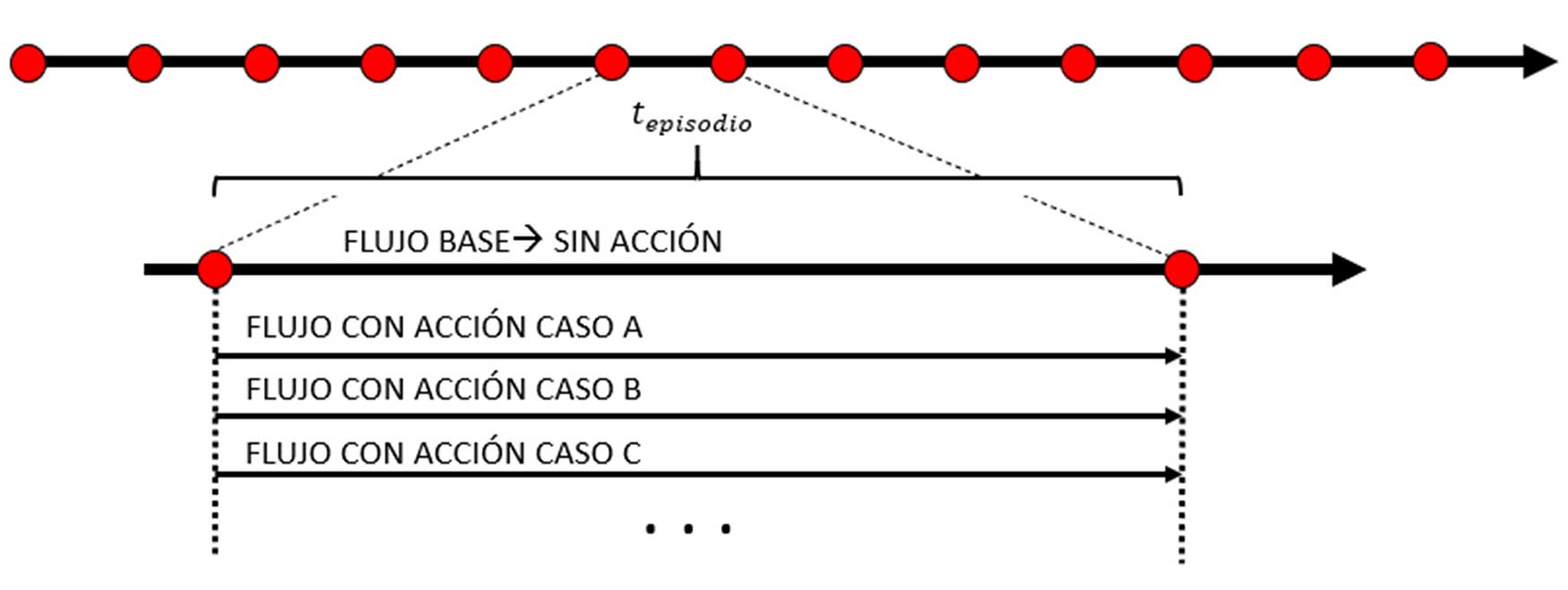
Para poder analizar el impacto, se decidió guardar las historias temporales de ciertas variables de interés como son: t_w (x, z) los esfuerzos cortantes en la pared; p_w (x, z), la presión en la pared; el consumo energético de los forzados; y las fluctuaciones de velocidad horizontal u(x, y, z) y vertical v(x, y, z).

Por otro lado, para resolver las ecuaciones del flujo, se ha empleado un solver pseudoespectral que sigue el algoritmo propuesto por Kim, Moin y Moser [9], con 128³ puntos y un mallado exponencial en la dirección normal a la pared, lo que nos permite tener una discretización del flujo suficientemente buena como para no perder información.

Tras un análisis profundo de las variables guardadas/bajo observación, algunos de los principales resultados obtenidos fueron los siguientes:

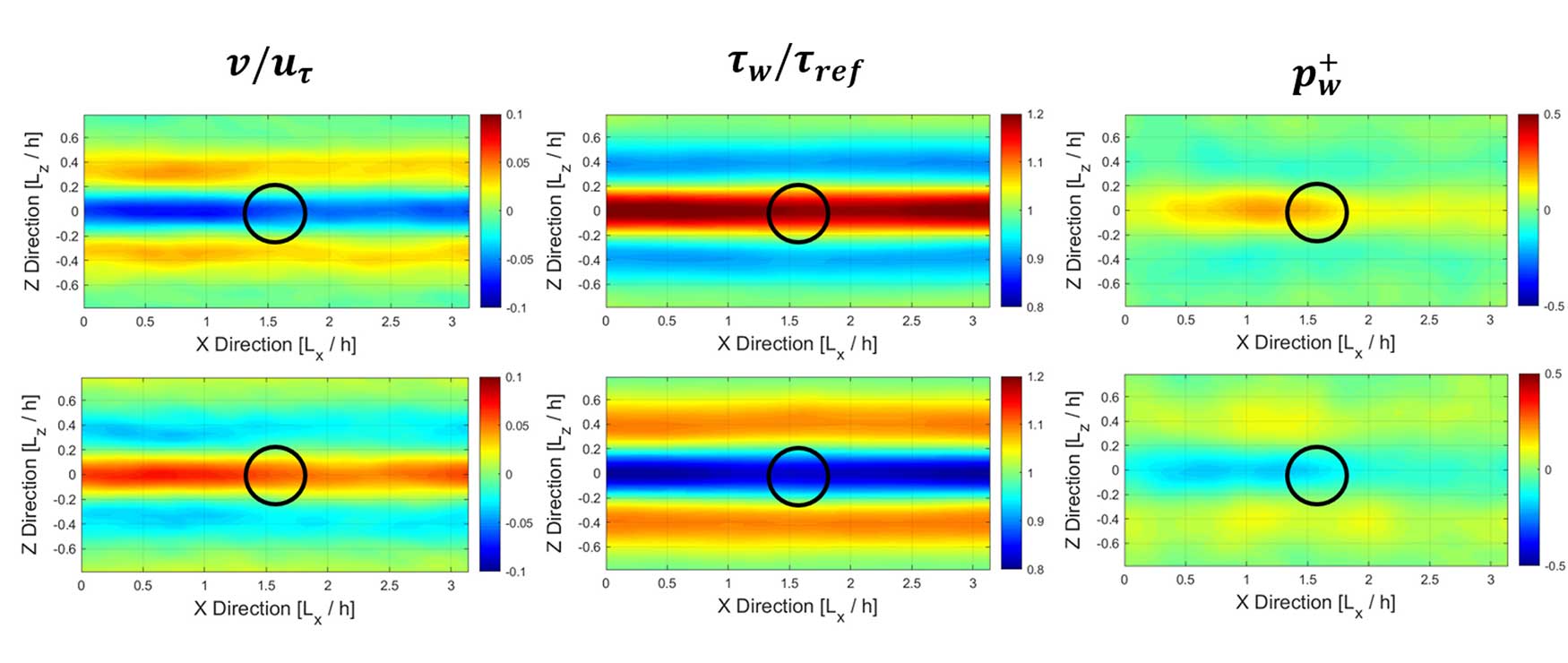
• Los datos muestran la existencia de regiones características dependiendo del forzado empleado para obtener nuestro objetivo final, la reducción de la fricción de la piel. Estas regiones se observan principalmente en los campos de las variables guardadas, especialmente en los esfuerzos cortantes y las fluctuaciones de la velocidad vertical, y en menor medida en la presión.
• La convergencia de los campos (ver ilustración 3) muestra que las regiones son claramente dependientes del forzado empleado (positivo o negativo), especialmente en el caso de las fluctuaciones de velocidad verticales y los esfuerzos cortantes. Además, estos resultados muestran concordancia con los estudios de control por oposición. Por otro lado, los campos de presión parecen no haber convergido del todo, aunque se aprecian regiones interesantes de analizar. De hecho, la correlación observada entre los esfuerzos cortantes y la presión sugiere un estudio futuro en mayor profundidad. La definición de sensores de presión y cortadura aguas arriba del forzado (izqda. en las imágenes) muestran una buena predicción de los forzados a emplear [10].
• Los resultados obtenidos para el resto de los forzados muestran conclusiones análogas a las presentadas con anterioridad. Sin embargo, a medida que aumentamos su tamaño (en espacio y tiempo) se muestra un incremento de la fricción de la piel independientemente del sentido del forzado. Esto es probable que se deba a efectos numéricos y a las dimensiones del canal empleado. Es por ello por lo que se propone continuar con este estudio en canales de mayor tamaño y mayores Ret para observar el efecto de los forzados en otras regiones de la capa límite.
• Su aplicación desde un punto de vista práctico en las alas de las aeronaves muestra que con actuadores del orden de milímetros y separados distancias del orden de centímetros, estos podrían proveer reducciones de la fricción de la piel de entorno a un 2% en condiciones de vuelo en crucero.
• Por último, este estudio nos ha dado la oportunidad de definir un mapa preliminar que podrá permitir el control de actuadores de manera autónoma en función del estado del flujo. El objetivo final de este mapa sería entrenar a un algoritmo que buscase la optimización mediante la experiencia.

Agradecimientos

Me gustaría agradecer a mis dos tutores O. Flores (UC3M) y A. Vela-Martín (UPM) por todo el esfuerzo y dedicación aportados. Esta investigación ha sido financiada por el European Research Council bajo la subvención COTURB ERC-2014.AdG-669505 a través del Madrid Summer Programme, 2019.

Referencias

[1] IATA, Fuel fact sheet, May 2019.

[2] S. Tardu, Wall turbulence control. John Wiley & Sons, 2017.

[3] M. Abbassi, W. Baars, N Hutchins, and I Marusic, ‘Skin-friction drag reduction in a high-reynolds-number turbulent boundary layer via real-time control of largescale structures’, International Journal of Heat and Fluid Flow, vol. 67, pp. 30–41, 2017.

[4] H. Choi, P. Moin, and J. Kim, ‘Active turbulence control for drag reduction in wall-bounded flows’, Journal of Fluid Mechanics, vol. 262, pp. 75–110, 1994.

[5] E. Hammond, T. Bewley, and P Moin, ‘Observed mechanisms for turbulence attenuation and enhancement in opposition-controlled wall-bounded flows’, Physics of Fluids, vol. 10, no. 9, pp. 2421–2423, 1998.

[6] J. Yun and J. Lee, ‘Opposition control of turbulent channel flow with wall pressure using deep neural network’, Bulletin of the American Physical Society, 2018.

[7] J. Park and H. Choi, ‘Prediction and control of turbulent channel flow with deep learning’, Bulletin of the American Physical Society, 2018.

[8] J. Jiménez and P. Moin, ‘The minimal flow unit in near-wall turbulence’, Journal of Fluid Mechanics, vol. 225, pp. 213–240, 1991.

[9] J. Kim, P. Moin, and R. Moser, ‘Turbulence statistics in fully developed channel flow at low reynolds number’, Journal of fluid mechanics, vol. 177, pp. 133–166, 1987.

[10] R. Pastor, A. Vela-Martin and O.Flores ‘Wall-bounded turbulence control: statistical characterisation of actions/states’. (2020) arXiv preprint arXiv:2002.08852.