Fachada ultra transparente mediante la unión de componentes de vidrio con silicona estructural, creando un conjunto de efecto membrana
Este artículo es un extracto del trabajo de TFM presentado en la edición 2024 del Máster de Fachadas Ligeras de la Universidad del País Vasco (EHU - UPV). En el mismo se describe la resolución de un módulo teórico de 8 metros de fachada ultratransparente, mediante el uso de vidrio como elemento portante, sin utilizar elementos de refuerzo o de conexión de otros materiales y utilizando únicamente montantes de vidrio como rigidizadores en los extremos de cada módulo.
El vidrio es uno de los materiales de construcción más determinantes en el diseño de fachadas, siendo usado no solamente por su carácter transparente, sino también como reclamo icónico y de atracción. A su vez, las grandes fachadas de ‘todo vidrio’ están asociadas a un alto nivel tecnológico ya que, hasta no hace mucho tiempo, el vidrio ha tenido limitado su uso a material de relleno dentro de una cuadrícula estructural a la que confiaba la resistencia mecánica mediante montantes y travesaños de aluminio o acero. Esto se ha debido principalmente a su fragilidad y a su rotura inmediata al alcanzar su límite elástico. Pero ¿qué ocurre si comparamos sus propiedades mecánicas con la de otros materiales? El vidrio tiene un Módulo elástico similar al aluminio y una resistencia a compresión superior al hormigón armado, teniendo su talón de Aquiles en una mucho menor resistencia a tracción, lo que afecta directamente a su resistencia a la flexión.
A pesar de no tener una normativa europea de referencia para el cálculo y verificación de estructuras de vidrio, desde los años 70 se han desarrollado innumerables proyectos de este tipo, siendo su crecimiento exponencial en los últimos años. A destacar, que en los últimos años se viene desarrollando el proyecto de Eurocódigo, publicado en el año 2023 como borrador, para el diseño y la validación de elementos estructurales de vidrio, donde se desarrollan los requisitos de resistencia, aptitud para el servicio, características de fractura y consecuencias del fallo de componentes en relación con la seguridad de las personas, robustez, redundancia y durabilidad de las estructuras de vidrio y que será la norma de referencia para el desarrollo de este trabajo.
1. Punto de partida
El punto de partida de este proyecto fin de máster ha sido la fachada de varios pabellones que desarrollé durante mis años de trabajo en la empresa japonesa Nikken Sekkei, para el proyecto del nuevo estadio Camp Nou en Barcelona. Un proyecto de fachada en el que estuve particularmente implicado y que fue diseñada originalmente con vidrio estructural, el cual evolucionó hacia un sistema de fachada stick tradicional.
Partiendo de esta base, el objetivo primordial de este TFM ha sido el resolver un módulo teórico de una fachada ultratransparente, sin usar elementos de refuerzo o de conexión de otros materiales, mediante la utilización de vidrio de grandes dimensiones como elemento portante teniendo el menor número de elementos rigidizadores (montantes de vidrio) posibles.
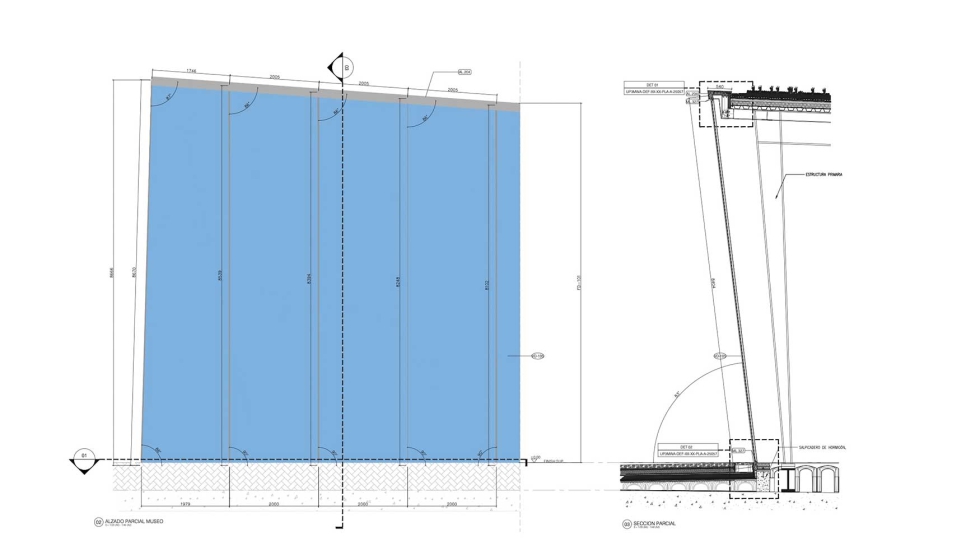
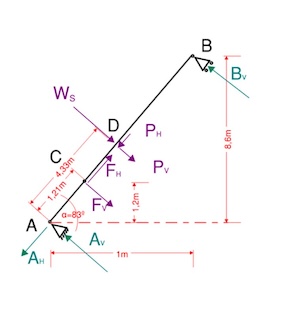
El módulo de estudio elegido es de aproximadamente 8m de ancho por 8m de alto, comprende 4 paneles de una altura que varían desde 8,6m hasta los 8,1m de alto y un ancho de 2m cada uno. Los 4 vidrios analizados son parte de un mismo plano con una inclinación de 83º hacia el exterior, siendo sus aristas verticales paralelas entre sí en los 3 paneles interiores y en el de esquina con su arista exterior inclinada un ángulo de 88.43º hacia el interior. Las aristas inferiores son rectas y perpendiculares a las verticales (excepto en el caso de la esquina, con 88,43º) y las superiores forman parte de un mismo plano inclinado 85.83º con la vertical (salvo en el caso de la esquina, con 87.40º).
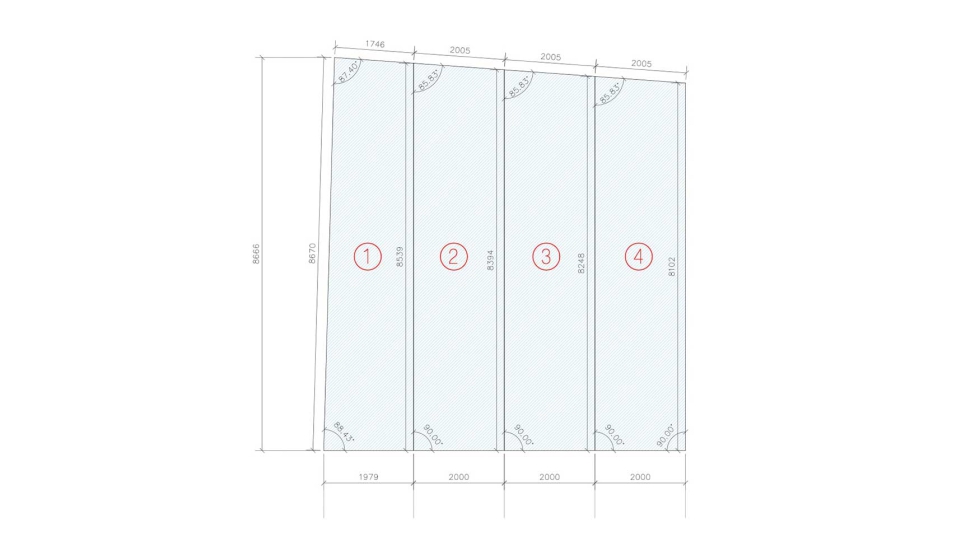
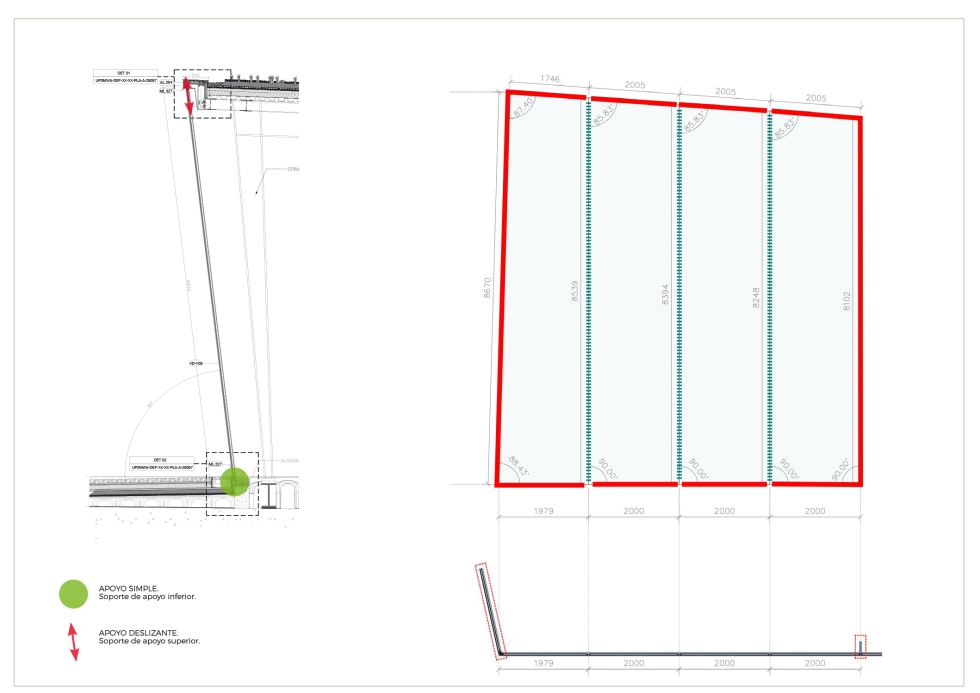
Cuentan con un apoyo simple en su base y deslizante en el plano del vidrio en la parte superior, evitando el vuelco y trasmitiendo empujes horizontales, pero permitiendo el movimiento y dilataciones en el plano del vidrio.
2. Hipótesis
La hipótesis de partida, es que mediante el pegado con silicona estructural se arriostrarán los 4 paneles entre sí formando una sola placa. La fachada lateral y una cartela cada 4 módulos serán los únicos elementos rigidizadores en el plano perpendicular de la fachada y los encargados de absorber los esfuerzos de viento y las cargas horizontales. Por lo que;
- Es posible hacer funcionar un módulo de 4 paneles de vidrio, como una placa de vidrio teórica apoyada en 4 lados haciendo que paneles independientes que físicamente están apoyados en 3 y 2 lados, mediante su unión con silicona estructural en sus lados longitudinales, tengan un comportamiento de membrana en su conjunto.
- Mediante el comportamiento de membrana podemos optimizar el espesor y la composición del vidrio final.
3. Cálculo
3.1 Predimensionado
Comenzamos el cálculo con un predimensionando del espesor del panel de vidrio, para ello, limitamos la deformada que produce el peso propio del vidrio a L/500 ya que este valor hace que la curvatura producida por la flecha sea imperceptible al ojo humano y con esta variable predimensionamos su espesor, resultando un valor de 46,50mm.
Posteriormente, procedemos a predimensionar el montante o cartela de vidrio. Para ello, limitamos la deformada producida por el viento de succión (previamente calculado según EUROCÓDIGOS) a L/200 o 15mm, tomando el menor valor de éstos.
- Wsucción = -1,22 KN/m2
- Wpresión = 0,87 KN/m2
Fijamos un espesor de montante de 36mm y el resultado es un valor de 610mm de profundidad.
3.2 Funcionamiento del módulo como membrana
El siguiente paso, ha sido realizar un análisis completo de nuestra área de 4 módulos con los valores del predimensionado, analizando su comportamiento como membrana y lo compararemos con un módulo formado por un único vidrio teórico. Esta comprobación nos servirá de base para corroborar la hipótesis de que nuestra fachada en ningún caso funcionará como una viga biapoyada, sino que todos los paneles unidos con la silicona estructural funcionarán como una membrana donde el objetivo es asimilar la unión de los 4 vidrios a una 'macro-placa de vidrio' que se considera apoyada en sus 4 lados.
Modelamos ambos casos en el programa de cálculo de elementos finitos MECWAY y con el solver Calculix aplicamos las condiciones de contorno, las correspondientes cargas de viento y peso propio, tras usar un cálculo estático no lineal 3D tendremos los siguientes valores de tensiones y deformación:
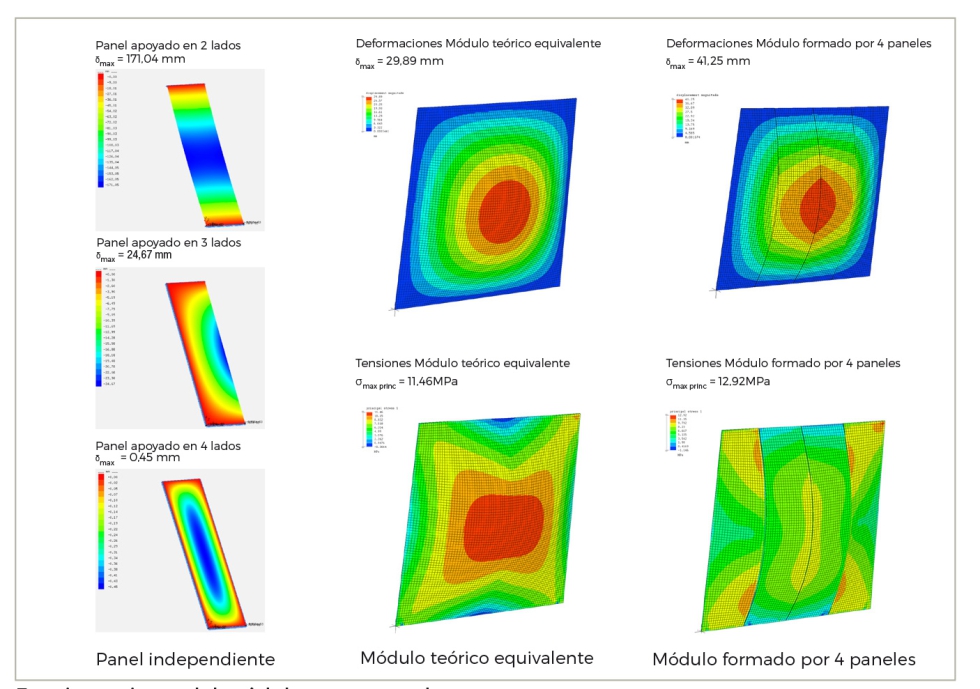
Al analizar los resultados, vemos que el comportamiento es más óptimo obviamente en la placa teórica, pero aun así son valores del mismo orden de magnitud, por lo que nuestra hipótesis es correcta.
3.3 Cálculo del panel de vidrio
Tras corroborar que el comportamiento de nuestro módulo se asemeja a una macroplaca, procedemos al cálculo de la composición de nuestros paneles de vidrio, mediante su verificación según la peor combinación de cargas entre el peso propio del vidrio, el empuje producido por el viento y un empuje lineal horizontal de 1,6 kN/m aplicado a 1,2 metros sobre nivel del suelo ('Cargas sobre elementos divisorios' según CTE SE-AE 2009).
Se verifica la tensión máxima admisible con los Estados Límites Últimos y la flecha máxima admisible con Estados Límites de Servicio. Para conseguir el valor del espesor monolítico equivalente usamos el método de espesores efectivos para vigas de vidrio multilaminado con placas del mismo espesor sometidas a flexión mediante ‘Enhanced Effective Thickness’ (EET).
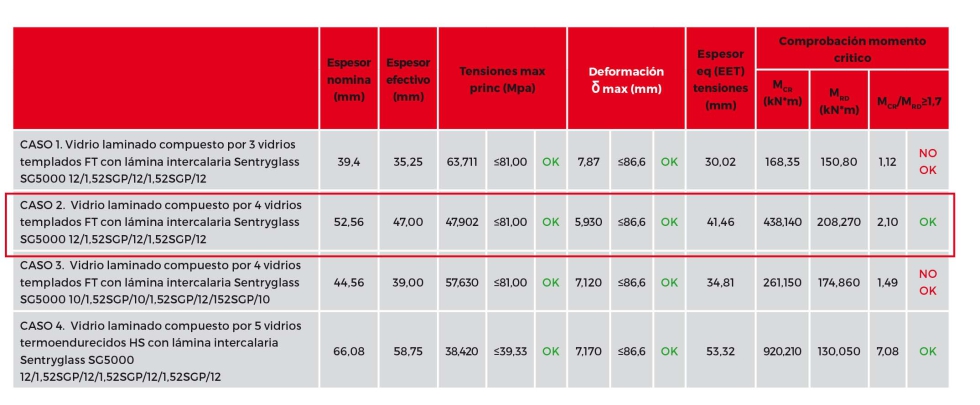
Iteramos con diferentes composiciones de vidrio laminado que existen en el mercado y tras su análisis, se elige la más optima que cumpla con todas las comprobaciones.
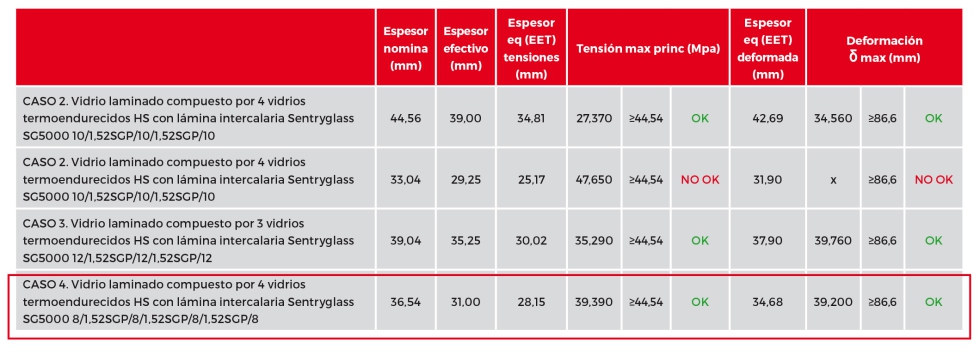
3.4 Verificación de la silicona estructural
Para verificar las tensiones máximas de diseño de la silicona, se ha de analizar los valores de tensiones Von Mises de la silicona en cada uno de nuestros casos de estudio en elementos finitos para los paneles de vidrio de nuestro modelo contra los datos proporcionados por SIKASIL, eligiendo el tipo SIKASIL SG-500. Estos datos son válidos para elementos volumétricos y modelos hiperelásticos del material Sikasil:
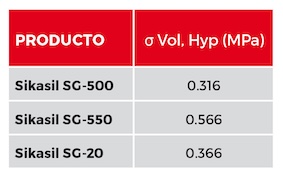
Aunque estos datos no serían válidos para cargas permanentes y teniendo en cuenta que en nuestro caso de estudio estamos incluyendo el peso propio (permanente), su carga principal es la carga variable de viento por ser la más desfavorable y es por esto que consideramos la verificación correcta. A pesar de todo, sabemos que cuando se respeta el valor máximo de tensión de diseño de 0,21 MPa, este método de calibración es correcto ya que nos quedamos siempre del lado de la seguridad.
Con esta verificación de tensión máxima de diseño confirmamos la ideonidad de la silicona considerándola como un material lineal. Pero sabemos que la silicona es un polímero que se define como elastómero sintético y que presenta viscoelasticidad. Es por este comportamiento por el que si el material está sometido a un desplazamiento constante (como puede ser la deformación por peso propio) se produce una relajación de las tensiones del material a largo plazo que permite más deformación y que puede puede llevar al material a una fractura por alcanzar el valor último de deformación cuando aun está lejos de su valor máximo de tensiones. Es decir, una tensíón puntual elevada no genera necesariamente una fractura, pero alcanzar el valor último de deformación unitaria si.
Por esto, añadimos la verificación de la deformación unitaria principal de la silicona (principal strain). En esta comprobación, para el caso de cargas permanentes la deformación principal máxima que usaremos será del orden de magnitud εstrain, max ≤ 15%, mientras que para cargas de viento un valor del lado de la seguridad será εstrain, max ≤ 90%.
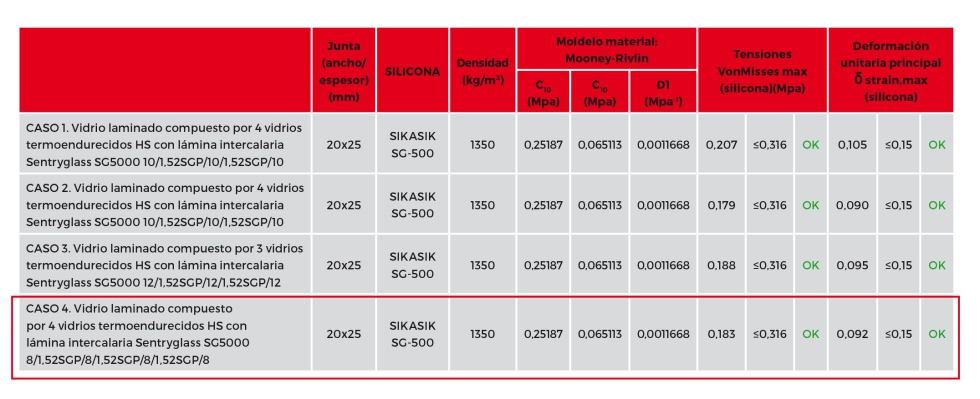
3.5 Cálculo del montante de vidrio
A continuación, verificamos el montante con cálculo manual como viga biapoyada según la peor combinación de cargas entre el peso propio del vidrio, el empuje producido por el viento en medio módulo a cada lado del montane (8m) y un empuje lineal horizontal de 1,6 kN/m aplicado a 1,2 metros sobre nivel del suelo ('Cargas sobre elementos divisorios' según CTE SE-AE 2009).
Se ha de comprobar la tensión máxima admisible con los Estados Límites Últimos y la flecha máxima admisible con Estados Límites de Servicio y calculando tensiones y deformaciones usando el espesor monolítico mínimo (suma de los valores característicos de cada lámina) ya que se trata de cargas en el plano del vidrio ‘In Plane’ y el intercalario no influye.
Iteramos con diferentes composiciones de vidrio laminado que existen en el mercado y tras su análisis se ha de elegir, la más optima que cumpla con todas las comprobaciones: resistencia a pandeo lateral de secciones esbeltas con el momento crítico y verificación y comprobación nuevamente de tensiones, pandeo y momento crítico con un componente del laminado roto.
- Estados límites últimos para tensiones
σ: = N/A + M/Wei = 47,9024 MPa
Nuestro valor de σmax admisible según lo establecido en la norma prEN 19100 y calculado en el capítulo 8 punto 5. Resistencia de diseño del vidrio según prEN 19100 para IN PLANE LOADS será de 39,33 MPa para vidrio termoendurecido y de 81 MPa para templado.
σmax adm (39,33 MPa) ≤ σmax princ (47,90 MPa) NO CUMPLE para Vidrio Termoendurecido
σmax adm (81 MPa) ≤ σmax princ (47,90 MPa) CUMPLE para Vidrio Templado
- Estados límites de servicio para deformaciones
δmax = 5,93 mm
En la norma prEN 19100_3 (referente a in-plane loads) no se menciona ningún requerimiento para la limitación de la deformada máxima, pero sabemos que según la norma Australiana AS1288-2006: Glass in buildings – selection and installation, si no hay ningún requerimiento específico para la limitación de la flecha, ésta debe limitarse a L/65 ó 50mm, siendo L:
- La dimensión del lado libre mayor para vidrios cogidos a 2 lados
- La dimensión del lado libre para vidrios cogidos a 3 lados
- La dimensión menor para vidrios cogidos a 4 lados
Nuestro montante está cogido a 3 lados, por lo que:
L: = 8660 mm
L/65= 133,23 mm ≥ 50 mm
fmax (50 mm) ≥ δmax (5,93 mm) OK
Este valor de deformada cabe destacar que es significativamente bajo, de un orden de magnitud de L/1000 por lo que será imperceptible al ojo humano.
4. Simulación módulo completo en elementos finitos
Una vez predimensionados, calculados y verificados cada elemento de manera independiente, se ha de proceder a modelar y simular el módulo completo en elementos finitos para su verificación final como conjunto.
Para ello, usamos de nuevo el programa de cálculo de elementos finitos MECWAY con el solver Calculix. Tras modelar dos módulos completos de 4 placas (uno a cada lado del montante para replicar las cargas que aplicarían en un montante real) y sus correspondientes cordones de silicona de unión entre placas, añadimos el montante uniendo este a los extremos de los dos módulos con sendos cordones de silicona, haciendo que los nodos de todos estos cordones sean coincidentes con los de los vidrios para que al realizar el cálculo los esfuerzos se transmitan correctamente.
Realizamos dos modelos, uno para los Estados Límites Últimos y otro para los Estados Límites de Servicio cada uno de ellos con sus cargas y espesores correspondientes según los casos más óptimos elegidos en el cálculo individual.
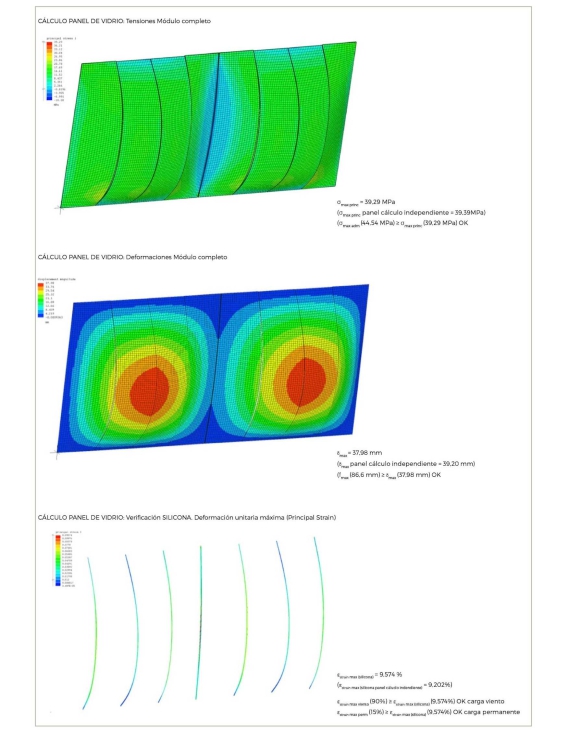
4.1 Panel de vidrio y silicona estructural: nuestros resultados para la simulaci`ón completa son similares al cálculo individual.
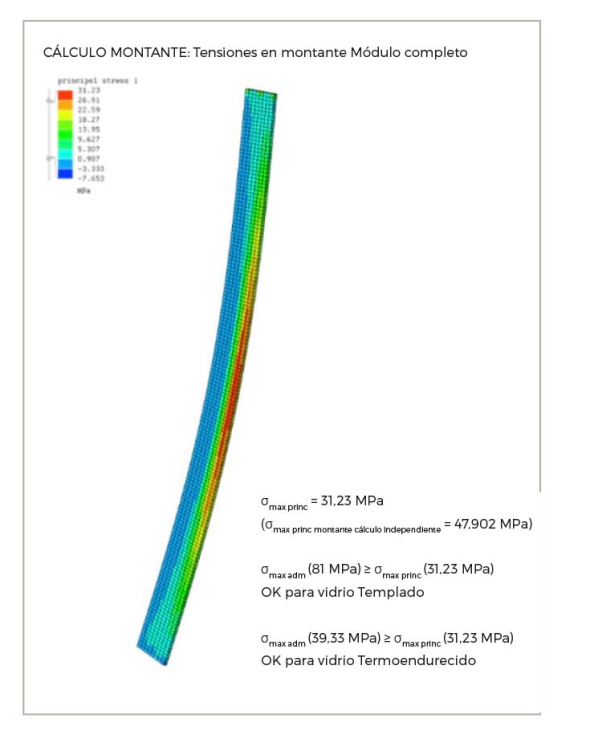
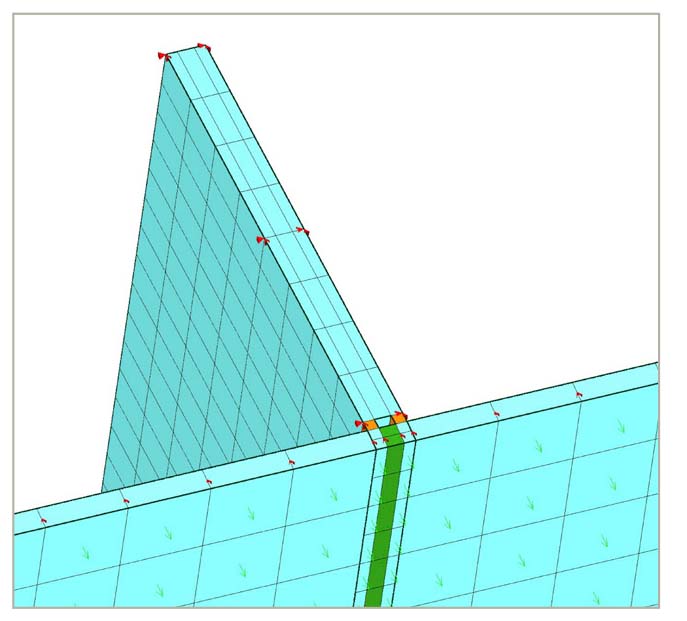
4.2 Montante: optimización
En el caso del montante, el nuevo resultado comparado con el cálculo individual es menor, aproximadamente en un tercio. Esta diferencia, se produce por la colaboración geométrica del canto longitudinal de los paneles, que unidos con la silicona, forman una geometría de viga en T que rigidiza el canto del montante, produciendo una menor deformación y exigiendo al montante una tensión menor.
5. Conclusiones
Como conclusiones podemos plasmar las siguientes:
- Se ha cumplido la principal hipótesis de partida, demostrando que es posible hacer funcionar un módulo formado por la unión de diferentes paneles con silicona estructural sin elementos de refuerzo.
- Se ha probado mediante la simulación en elementos finitos que este módulo trabaja como una macro placa, asimilando su comportamiento al de una membrana en su conjunto.
- Se ha corroborado que al hacer funcionar el módulo como una placa es posible reducir y optimizar el espesor final del vidrio, sobre todo en el caso de los paneles centrales en situación de vigas biapoyadas, que hubieran resultado inviables debido al gran tamaño de nuestro panel y su consecuente deformación.
- Se ha profundizado en el funcionamiento no lineal del vidrio cuando trabaja como una placa y se ha aplicado para optimizar los resultados.
- Se ha confirmado con la simulación por elementos finitos del módulo completo, que el funcionamiento en conjunto de los paneles junto con el montante ha permitido optimizar la cartela y reducir las tensiones en aproximadamente un tercio. Esta diferencia de valor la podemos explicar por la colaboración geométrica del canto longitudinal de los paneles, que unidos con la silicona, forman una geometría de viga en T. Esta viga rigidiza el canto del montante, produciendo una menor deformación y exigiendo a este una tensión menor.
- Se ha expuesto mediante las simulaciones por elementos finitos, que es muy importante definir con claridad las condiciones de contorno, entenderlas y modelarlas lo más fidedignamente posible a las condiciones reales, ya que influyen de manera significativa en los resultados, pudiendo llegar a desvirtuar los valores finales.
- Se evidencia la necesidad urgente de la aprobación de una normativa europea de referencia para el vidrio estructural. Actualmente al no existir un marco normativo claro para el vidrio estructural, se terminan usando en muchos casos normas de otros países, a veces combinándose entre sí, y pudiendo llegar a aplicar diferentes criterios para la verificación y el cálculo en un mismo proyecto.
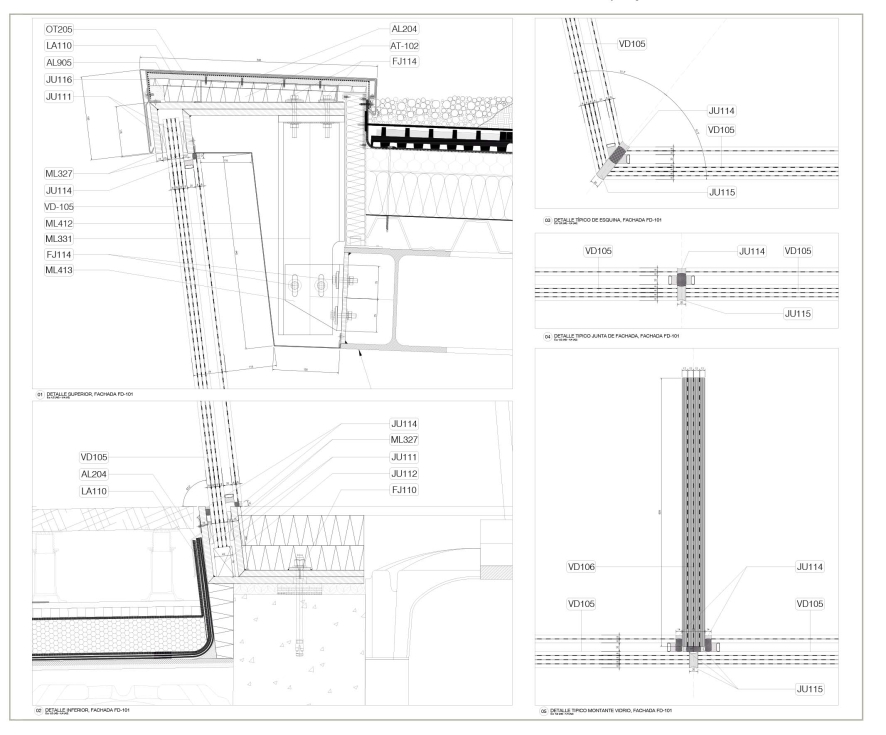
6. Proceso de montaje