Diseño térmico automático de moldes para piezas ópticas en moldeo por compresión

La metodología utilizada es el diseño térmico inverso del molde, que calcula el equilibrio térmico óptimo en el molde basándose en las propiedades térmicas de la pieza. De estas distribuciones de temperatura puede derivarse un comportamiento homogéneo de la contracción. La evaluación de las condiciones óptimas de refrigeración en la pieza presupone una función de calidad adecuada. Debido a la variedad de materiales, geometrías y morfologías que resultan del moldeo por inyección, una función de calidad validada para piezas de pared delgada debe verificarse para diferentes formas. Por lo tanto, en una optimización numérica se utilizan diferentes funciones de calidad que califican diferentes variables de estado dentro de la pieza y se comparan los resultados de temperatura y densidad. Se utilizan dos enfoques adecuados. Un enfoque tiene en cuenta la desviación de la temperatura durante la transición vítrea y el otro la influencia de la velocidad de enfriamiento. El entorno del proceso es una lente óptica moldeada por compresión con diferentes espesores de pared variables. Debido a la naturaleza de este proceso, la presión pertinente en la masa fundida se calcula con un modelo termomecánico.

La contracción de los componentes relacionada con el material es uno de los mayores retos de la transformación moderna de plásticos. Esto afecta especialmente a los componentes moldeados por inyección, que se caracterizan por una alta densidad funcional y geometrías de componentes cada vez más complejas. La contracción se ve afectada por muchos factores de influencia diferentes, como las condiciones de procesamiento, la humedad, las condiciones posteriores a la contracción, etc. Estos efectos se superponen, lo que da lugar a una contracción de la pieza localmente diferente que debe preverse durante la fase de diseño del molde. El reto general es que los clientes suelen tener grandes exigencias en cuanto al aspecto de la superficie y la estabilidad geométrica.

De todos los parámetros mencionados, el sistema de templado del molde es uno de los que más influye en la calidad de la pieza resultante. A diferencia de los parámetros de transformación, el sistema de templado es muy difícil de modificar una vez fabricado el molde. En el caso de piezas complejas moldeadas por inyección, a menudo no es posible diseñar un sistema de templado óptimo basándose únicamente en la experiencia del diseñador del molde. El desarrollo de un método altamente automatizado y reproducible para el diseño del molde térmico tiene un gran potencial para lograr una mayor precisión de moldeo. Además, se puede ahorrar tiempo y dinero. Las iteraciones habituales del molde de inyección antes del inicio de la producción pueden reducirse considerablemente. Además del alabeo resultante de la pieza, en el caso de los componentes ópticos es necesario tener en cuenta las tensiones internas, ya que influyen significativamente en la calidad óptica resultante. En los últimos años se han desarrollado varios enfoques diferentes para automatizar el paso de diseño del molde térmico, que se presentarán en el curso posterior de este artículo.

Con el auge de las tecnologías de fabricación aditiva, el diseño del molde térmico adquiere una importancia aún mayor. Mientras que la geometría de la cavidad puede editarse antes del postcurado del molde fabricado aditivamente, el diseño del canal de templado cerrado no puede adaptarse. No obstante, la idea de canales de refrigeración conformados que extraen el calor exactamente en el lugar donde es necesario resulta cada vez más convincente para las aplicaciones industriales. Cuanto más se acerca el canal de templado a la superficie de la cavidad, mayores son los gradientes resultantes, lo que hace que estas disposiciones sean propensas a errores en el diseño del molde térmico. Es necesario realizar cálculos precisos para crear un diseño de molde térmico adecuado.

Muchos grupos de investigación trabajan en el campo de la generación automática de canales de refrigeración. Feng et al. han realizado recientemente una extensa revisión bibliográfica. Agrupan los enfoques científicos en cinco categorías:

• Diseño basado en experimentos
• Diseño y optimización basados en la línea de refrigeración conforme
• Optimización mediante algoritmos expertos
• Diseño modular / paramétrico de canales de refrigeración conformados
• Modelado sólido basado en la optimización de la topología

La primera categoría es un enfoque práctico, en el que se crean diferentes diseños a través de la experiencia y luego se validan mediante simulaciones. Este método es costoso debido a su naturaleza iterativa y el resultado depende en gran medida de la experiencia del ingeniero. En la segunda categoría, los canales de refrigeración se optimizan geométricamente manteniendo una distancia constante a la pieza moldeada. Se trata de un enfoque muy interesante, ya que es muy rápido en términos de tiempo de cálculo. Sin embargo, no tiene en cuenta los diferentes espesores de pared ni la demanda variable de refrigeración para geometrías complejas. En la categoría de “Optimización mediante algoritmos expertos” pueden resumirse varios enfoques matemáticos sofisticados. Sin embargo, para poder procesar estos algoritmos son necesarios conocimientos expertos. El diseño modular de canales de refrigeración conformados es una categoría, en la que se parametriza la forma de los canales de refrigeración (por ejemplo, el diámetro y/o la longitud. Estos enfoques generan resultados muy rápidos, pero no cubren necesariamente todas las soluciones posibles y, por tanto, no garantizan un mínimo absoluto de alabeo. En la categoría de optimización de la topología se resumen varios enfoques. Éstos mejoran, por ejemplo, la conductancia térmica local del acero para mejorar el equilibrio térmico del molde. Estos enfoques toman el diseño del canal de templado como una constante dada. Como puede verse, los distintos enfoques tienen sus ventajas e inconvenientes.

En el Instituto de Procesamiento de Plásticos (IKV) se ha centrado en los últimos años la metodología del diseño inverso del molde térmico. La ventaja es que no es necesario diseñar una disposición de templado inicial y, por lo tanto, en el futuro no será necesario disponer de conocimientos específicos sobre la disposición óptima. El enfoque se denomina diseño térmico inverso de moldes porque al final de la fase de enfriamiento se parte de un estado teórico óptimo de la pieza moldeada y se calculan iterativamente los flujos de calor respectivos en el molde para poder realizar este estado óptimo. Todo el proceso se basa en una optimización térmica, que utiliza una función de calidad para evaluar la calidad térmica de la pieza. A partir de los flujos de calor calculados en el acero del molde, puede obtenerse una disposición adaptada de los canales de templado.

Este método también se utiliza en el diseño de canales de refrigeración para aplicaciones ópticas. En el caso de las lentes ópticas moldeadas por inyección, el reto consiste en producir una lente sin tensiones para evitar un índice de refracción no homogéneo. Como estas lentes ópticas tienen espesores de pared elevados debido a sus requisitos físicos, se produce un tiempo de enfriamiento prolongado. En consecuencia, durante el enfriamiento se producen tensiones inducidas térmicamente y la variación del grosor de las paredes agrava el problema. El proceso de producción analizado en esta contribución se denomina moldeo por compresión. La fabricación de componentes ópticos es mucho más lenta que el moldeo por inyección normal y, por tanto, se utiliza el moldeo por compresión para maximizar la calidad de la superficie y el tiempo de contacto para una eficacia de enfriamiento óptima. En este método se aplican cargas externas adicionales mediante una disminución del volumen de la cavidad. Este proceso puede dar lugar a tiempos de enfriamiento más cortos. Sin embargo, debido a la presión ejercida sobre las zonas fluidas y sólidas de la pieza, pueden producirse otras tensiones complejas en función de la geometría. Estas condiciones del proceso modifican las exigencias del diseño del molde térmico. Sin embargo, el control de la temperatura del molde mediante un sistema de canales de refrigeración sigue teniendo un impacto significativo en la consecución de un perfil de tensiones uniforme. Por lo tanto, se utilizará un método modificado.

La metodología del diseño térmico inverso de moldes consiste en una optimización térmica del molde. Son necesarios ciertos pasos para realizar un cálculo práctico del balance térmico óptimo en el molde y extraer una disposición de canales de refrigeración de alta resolución local. La metodología general se muestra en la siguiente figura.

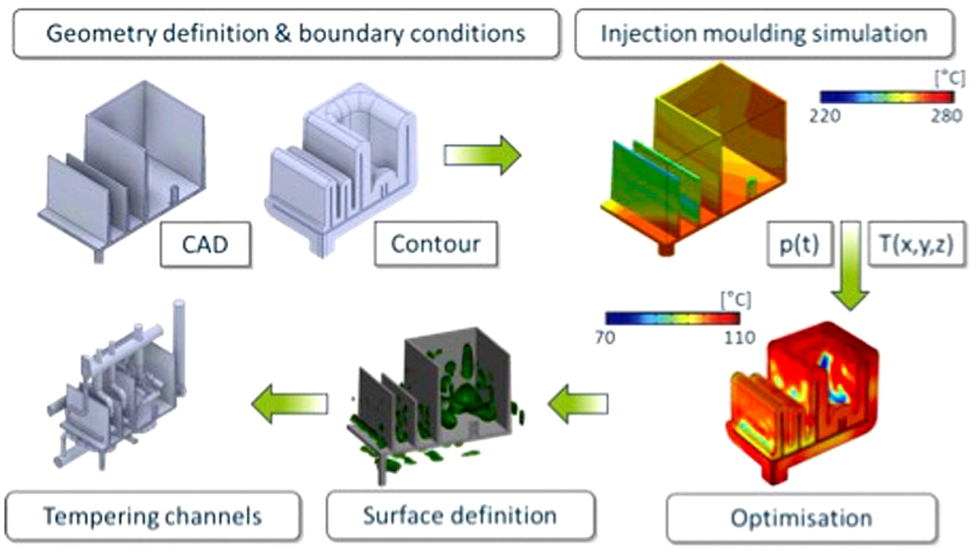
Figura 2.1: Metodología del diseño inverso del molde térmico

En primer lugar, se diseñan la geometría y las compensaciones necesarias. Para evitar la laboriosa optimización térmica de un molde completo en pasos posteriores, se diseña un contorno próximo a la pieza, que representa el volumen del molde (véase también la figura 2.2). Las temperaturas en el contorno del molde pueden ser adaptadas automáticamente por el algoritmo con respecto a la evaluación de una función de calidad. Además, se define un desplazamiento interior como segunda zona de evaluación. La configuración general del modelo se muestra a modo de ejemplo en la figura 1. En el siguiente paso, se realiza una simulación de moldeo por inyección sin canales de refrigeración para calcular la refrigeración a lo largo de la longitud de flujo durante la fase de llenado. A continuación, la distribución de temperatura y presión calculada mediante la simulación del proceso se transfiere al software de optimización, en el que sólo se tiene en cuenta la fase de refrigeración. En la fase de optimización térmica, se calcula una distribución óptima de la temperatura en el molde. A partir de esta distribución óptima de la temperatura, pueden extraerse superficies que localizan la posición óptima del canal de templado. Por último, se diseña una disposición del canal de templado.

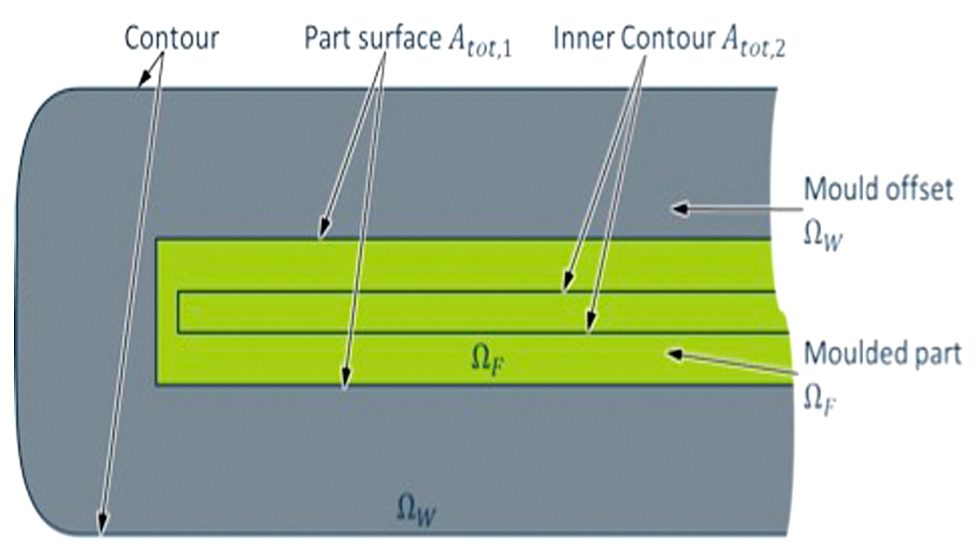
Figura 2.2: Vista detallada del contorno derivado

El algoritmo de optimización de la ejecución requiere una función de calidad que evalúe objetivamente la calidad de la pieza. Diferentes investigadores han definido ya varios enfoques, todos ellos con distintas ventajas e inconvenientes. Agazzi et al. utilizan un enfoque dependiente de la temperatura que no tiene en cuenta la compresibilidad del plástico fundido. Mientras que Nikoleizig amplía la función de calidad de Agazzi et al. y añade la evaluación de la densidad. El objetivo general de la función de calidad descrita por Nikoleizig puede describirse cualitativamente como:

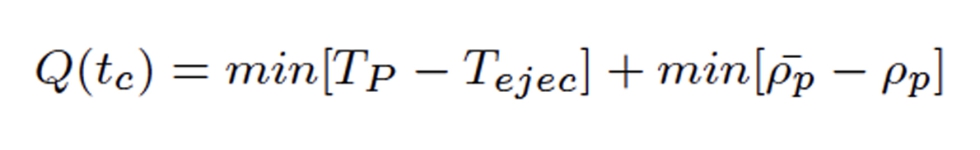
El objetivo de la función de calidad es minimizar la diferencia entre la temperatura local en la pieza T_P y una temperatura de eyección dada T_ejec. Al mismo tiempo, la densidad local no debe variar con respecto a la densidad global promediada al final de la fase de enfriamiento t _c.

La desventaja de este enfoque es que la densidad sólo puede evaluarse al final de la fase de enfriamiento, ya que una integración en cada paso temporal no es numéricamente factible. En consecuencia, este enfoque no tiene en cuenta la historia de enfriamiento del material, que es decisiva para la morfología del material. Para integrar el historial de enfriamiento, sería necesaria una integral temporal sobre la densidad durante la fase de enfriamiento, que suma las diferencias locales de densidad a lo largo del tiempo. Esta integral temporal teóricamente necesaria no puede realizarse en el software de optimización COMSOL Multiphysics, Comsol AB, Estocolmo, Suecia, porque conduce a tiempos de cálculo poco prácticos. Las pruebas para cuantificar el tiempo de cálculo se han abortado debido a su duración y al bloqueo de los recursos informáticos.

Sin embargo, la densidad depende exclusivamente de la temperatura al final del enfriamiento, ya que la presión se encuentra a nivel ambiente en toda la cavidad. En consecuencia, esto no aporta más información sobre la morfología en comparación con un enfoque puramente dependiente de la temperatura. Estas desventajas llevan a la idea de un nuevo enfoque para la descripción de la función de calidad.

Para el nuevo enfoque, se mantiene la evaluación de la temperatura al final del enfriamiento, ya que este término garantiza una estabilidad dimensional del material. Se establece la dirección de la optimización hacia una distribución homogénea de la temperatura. Este término de temperatura se valora negativamente si la temperatura local está demasiado alejada de la temperatura de desmoldeo. En caso contrario, se valora positivamente. En consecuencia, la temperatura de expulsión debe predefinirse y limita la optimización del proceso hacia un enfriamiento y un tiempo de ciclo cortos. Sin embargo, el objetivo de una distribución homogénea de la temperatura y un enfriamiento rápido son opuestos y no pueden optimizarse simultáneamente sin una comparación.

Un posible criterio de evaluación es la velocidad de enfriamiento. La velocidad de enfriamiento, especialmente a la temperatura de solidificación, determina la morfología del plástico. La homogeneización de este parámetro debería conducir a un menor alabeo de la pieza y a unas propiedades más homogéneas de la pieza moldeada. En particular, la velocidad de cristalización depende de la velocidad de enfriamiento local dentro del material. Así, la contracción puede verse influida por la integración de la velocidad de enfriamiento en la función de calidad. Debido a la mayor densidad de empaquetamiento, una tasa de cristalización más elevada conlleva una mayor contracción local. La homogeneización de este parámetro debería mejorar la contracción local sobre el volumen de la pieza.

En general, las piezas moldeadas por inyección experimentan diferentes velocidades de enfriamiento a lo largo del grosor de la pared. Cerca de la pared de la cavidad, se observa una alta velocidad de enfriamiento debido al contacto de la masa fundida caliente con el molde frío. En el centro de la pieza, la velocidad de enfriamiento es significativamente menor debido al aislamiento de la capa límite plástica. Como este efecto físico no puede modificarse, es importante generar propiedades homogéneas dentro de capas constantes alrededor del plano medio de la geometría de la pieza. Si las propiedades no son simétricas alrededor del plano medio, se genera un efecto de palanca y es de esperar que se produzcan alabeos. Estos aspectos conducen a la función de calidad de nueva formulación:

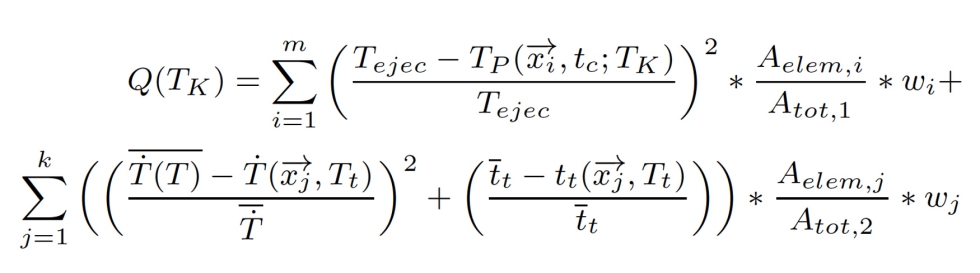
El primer término de la ecuación es muy similar a la función de calidad anterior de Nikoleizig. Evalúa la diferencia de temperatura en la pieza T_P respecto a la temperatura de desmoldeo T_ejec al final del enfriamiento t _c. Además, el término se normaliza en función de la temperatura de desmoldeo Tejec. Además, la influencia de la malla se considera mediante la variable A_elem, _i Esta fracción garantiza que cada nodo de temperatura sólo se considera por la parte de su elemento respectivo en toda la superficie o volumen de evaluación A_tot,1.

La segunda fila de la ecuación evalúa la morfología de la pieza moldeada. El primer término suma las diferencias de las velocidades de enfriamiento locales con respecto a una velocidad de enfriamiento promediada (T (T)). El segundo término evalúa el tiempo de solidificación. Estos dos términos se vuelven muy pequeños en el caso de una tasa de enfriamiento homogénea a un tiempo de solidificación similar. Ambos términos se evalúan en el A_tot,2 (véase la figura 2.2). A_tot,1 corresponde a la superficie de la pieza. A_tot,2 es una superficie desplazada en el interior de la pieza. El desplazamiento interior es necesario, ya que en la interfaz del molde y la masa fundida aparecen diferentes velocidades de enfriamiento en el acero y el plástico, lo que provoca inestabilidades numéricas en una optimización basada en gradientes. A partir de la evaluación en estas dos superficies, el algoritmo de optimización sustrae una distribución de temperatura en la superficie del molde tal que la función mostrada se convierte en mínima.

Ambos términos de la ecuación se ponderan con el factor _wj o _wi para conseguir los mejores resultados de optimización. Un análisis de sensibilidad de estos factores de ponderación muestra una mayor prioridad de la distribución de la temperatura para las piezas con un espesor de pared de 1 a 2 mm, ya que la conductividad térmica de los termoplásticos es relativamente baja. En consecuencia, hay que determinar si un grosor de pared diferente también consigue un mejor resultado según la función de calidad (véase la ecuación 2.2) con los mismos factores de ponderación.

La nueva función de calidad ya se ha aplicado y validado en dos geometrías de demostrador diferentes:

• una geometría de caja utilizada en investigaciones anteriores
• un pequeño demostrador de carcasa para una RaspberryPi utilizado por el IKV para la feria K de 2019.

Los resultados han demostrado que se pueden obtener resultados al menos similares a la función de calidad de Nikoleizig para ambas geometrías. Estas dos piezas tienen en común espesores de pared de 1 - 2 mm. En el siguiente paso de esta contribución se investigan otros componentes que se fabrican en el proceso de moldeo por inyección. Los componentes ópticos, como las lentes, requieren espesores de pared elevados para conseguir las propiedades ópticas deseadas. En el capítulo siguiente se explica una adaptación de la metodología a esta variante del proceso en forma de una función de calidad adaptada a este proceso. Finalmente, se compara la influencia de esta nueva función en el algoritmo de optimización con la nueva función de calidad para piezas de pared delgada.

El caso de uso es una lente indicadora tomada de una aplicación automovilística facilitada por Hella KG, Lippstadt, Alemania, para garantizar su validez práctica. Debido a las limitaciones de precisión, se suele utilizar el moldeo por compresión. Este presenta algunos saltos de grosor de pared en la parte superior y una lente alargada en la mitad inferior. En el proceso de moldeo por compresión, las dos partes del molde se mueven una hacia la otra y garantizan un contacto constante del molde con el plástico. Para garantizar la correcta transmisión de la luz, es obligatorio que la superficie sea de muy alta calidad. Para este complejo proceso, la optimización térmica debe ampliarse con cálculos termomecánicos para calcular con precisión la distribución de la presión en el interior de la pieza. El cálculo de esta distribución de presión es esencial para predecir correctamente el volumen específico local, que depende de la distribución de presión y temperatura (comportamiento pvT). La descripción precisa del comportamiento pvT es necesaria para una estimación precisa del alabeo esperado de la pieza. Además, la presión calculada se utiliza simultáneamente para determinar localmente el coeficiente de transferencia de calor dependiente de la presión y la conductividad térmica. Normalmente, la compresión mecánica sustituye a la fase de presión de mantenimiento.

El cálculo termomecánico dependiente de la temperatura en combinación con las múltiples iteraciones para la optimización aumenta significativamente el tiempo de cálculo, por lo que se opta por un enfoque bidimensional. Tras la validación de este enfoque, podría ser factible un cálculo tridimensional. En esta contribución, se utiliza un plano simétrico en la dirección longitudinal para los cálculos. Las dimensiones y la ubicación del plano de corte se visualizan en la figura 3.

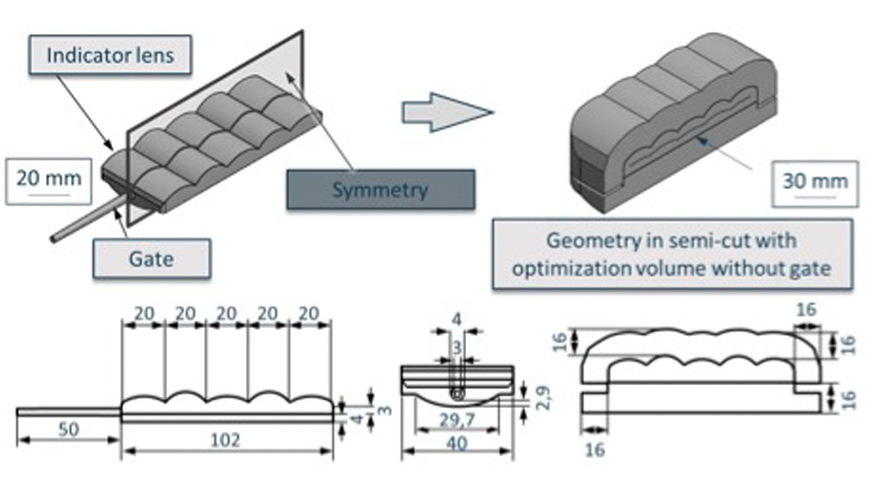
Figura 2.3: Dimensiones de la lente indicadora y del volumen de optimización.

El volumen del molde se divide en dos partes. La parte superior (lado de la boquilla) se fija mecánicamente y la parte inferior se define como el molde móvil con un movimiento lineal de 0,16 mm/s que se detiene a una compresión de 0,5 mm de la masa fundida de plástico que garantiza la compresión mecánica.

En el presente trabajo, sólo se ha utilizado una simulación dependiente de la temperatura para evaluar la calidad de la pieza moldeada. El enfoque se basa en dos criterios diferentes. Para conseguir una geometría de pieza estable, todo el volumen de la pieza debe estar por debajo de la temperatura de transición vítrea. Sólo cuando se alcanza esta condición, se puede minimizar la contracción física. La pieza debe alcanzar una distribución de la temperatura lo más homogénea posible. Por lo tanto, la temperatura de la superficie de la pieza se elige como objetivo de optimización, ya que se pueden obtener mejores resultados para un campo de temperatura evaluado con valores similares. La función de calidad basada en estos aspectos teóricos se define de la siguiente manera:

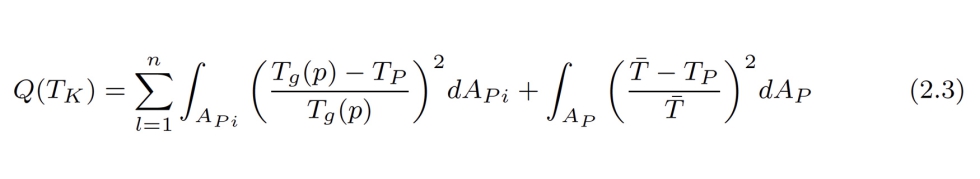
El primer término integra la diferencia normalizada entre la temperatura de la pieza T_P y la temperatura de transición vítrea T_g sobre A_Pi, que es el plano medio de la pieza. El objetivo del enfoque es enfriar hasta la temperatura de transición vítrea lo más rápidamente posible en cualquier punto de la pieza. El plano medio es el lugar más alejado de la superficie del molde y, por tanto, el último en solidificarse. Las diferencias de temperatura respecto a la temperatura de transición vítrea se ponderan negativamente. Además, la homogeneidad de la distribución de la temperatura en la superficie de la pieza A_P se evalúa mediante la diferencia normalizada entre la temperatura de la pieza y la temperatura media T.

El material utilizado para esta aplicación es un Plexiglas 7N de Roehm GmbH, Darmstadt, Alemania. La temperatura de transición vítrea de este material es de 113,85 °C. El comportamiento mecánico del material se modela termoelásticamente con el módulo de tracción dependiente de la temperatura (véase la tabla 2.1)

Tabla 2.1: Valores del módulo de Young.

A continuación, se realiza una comparación del enfoque puramente dependiente de la temperatura (véase la ecuación 2.3) con el enfoque que tiene en cuenta la morfología (véase la ecuación 2.2) en el plano de corte bidimensional en el centro de la pieza (véase la figura 2.3). En lo sucesivo, los enfoques se denominarán optimización/enfoque de la temperatura y optimización/enfoque de la morfología. El objetivo es evaluar si la optimización de la temperatura desarrollada específicamente para piezas ópticas de paredes gruesas consigue mejores resultados que la optimización de la morfología, que ha demostrado su eficacia en piezas de paredes finas. Sin embargo, el enfoque morfológico también tiene el potencial de determinar una solución mejor teniendo en cuenta la tasa de enfriamiento significativamente relevante y los valores de temperatura normalizados. El enfoque de la morfología se calcula con factores de ponderación que hacen hincapié en el impacto de la distribución de la temperatura. Las temperaturas y los parámetros de proceso especificados se muestran en la tabla 2.2. La optimización térmica comienza al final del llenado y tiene en cuenta toda la fase de compresión y enfriamiento.

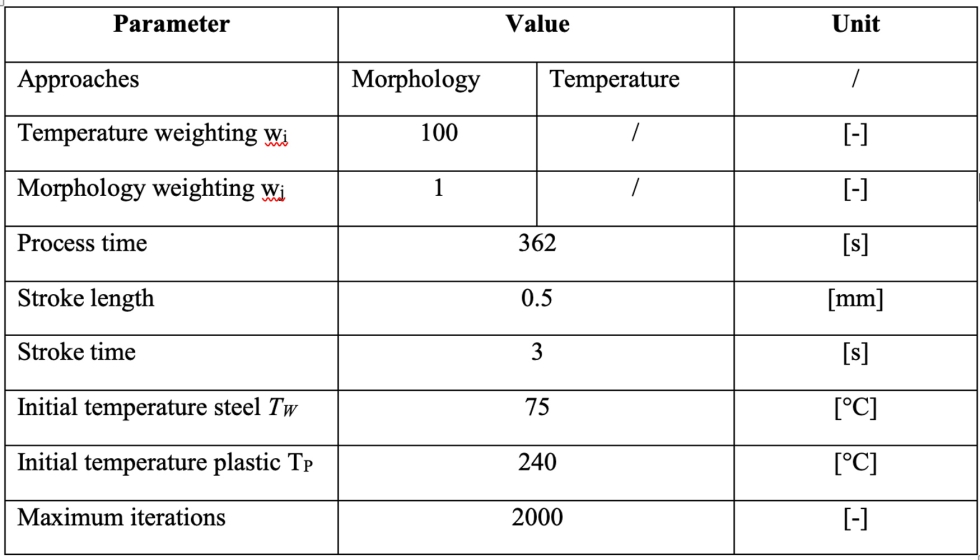
Tabla 2.2: Parámetros del proceso y factores de ponderación

La metodología del diseño térmico inverso del molde se detiene tras el paso de optimización térmica (ver Figura 2.2) y se realiza una comparación de los resultados de las dos optimizaciones.

En la siguiente Figura se muestra la distribución de temperatura calculada en la pieza moldeada al final del enfriamiento.

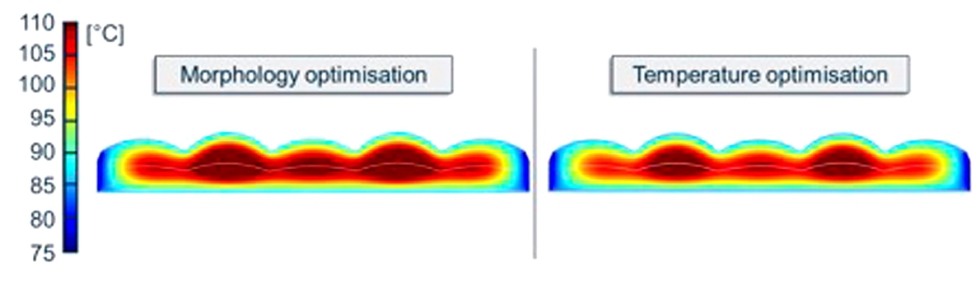
Figura 2.4: Distribución de la temperatura en la pieza al final del enfriamiento

Tabla 2.3: Temperaturas superficiales resultantes de las dos optimizaciones diferentes.

El objetivo del enfoque morfológico es alcanzar una temperatura homogénea de 85 °C en la superficie, mientras que el enfoque dependiente de la temperatura intenta alcanzar una temperatura de 110 °C, que es la temperatura de transición vítrea a presión ambiente en el plano medio. El enfoque morfológico se aproxima más a los 85 °C requeridos. En la figura siguiente, se visualiza la distribución de la temperatura en el plano medio (Figura 2.5).

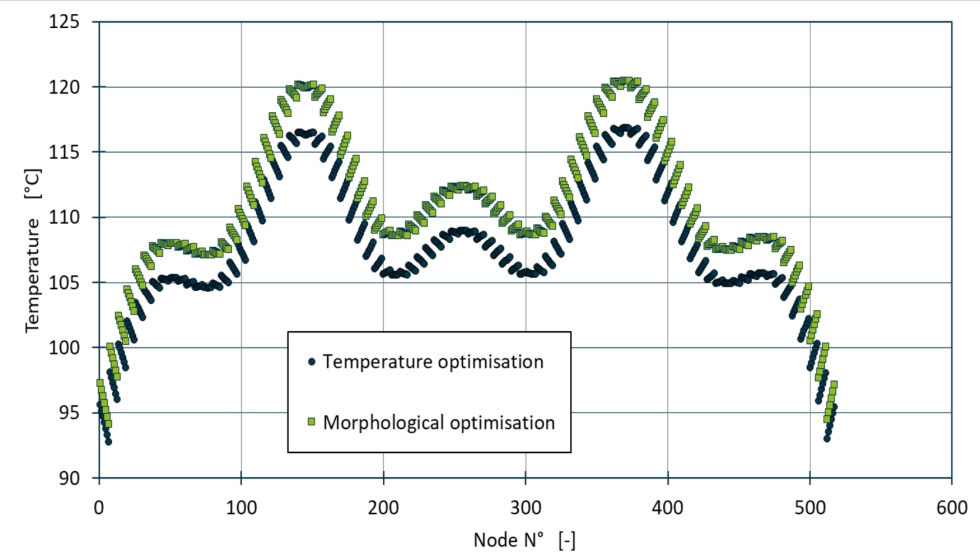
Figura 2.5: Distribución de la temperatura en la línea media.

Se puede observar que la temperatura fluctúa en función del grosor efectivo de la pared en los respectivos nodos. El plano medio en ambos extremos de la pieza es significativamente más frío, ya que esta zona puede enfriarse desde tres lados en el borde de la lente indicadora. El curso de las dos curvas de temperatura es muy comparable. Las desviaciones estándar son similares, pero se aprecia un desfase general de 3 °C.

En el siguiente paso, es necesario evaluar la morfología, que influye en el alabeo general esperado. Para comparar los resultados de forma significativa, en trabajos anteriores se ha considerado el valor de la función objetivo. Esto no es útil en este caso, porque la formulación de las dos funciones objetivo (véase la ecuación 2.2 y 2.3) y la ecuación es fundamentalmente diferente. Por lo tanto, resultan valores numéricos diferentes, que son comparables en el mismo modelo. No se pueden comparar enfoques diferentes. Para obtener una buena calidad de moldeo, es importante un curso homogéneo de la densidad a lo largo del tiempo. La presión y la temperatura locales influyen en la contracción local, que está representada por la densidad. Sin embargo, lo relevante no es el valor exacto de la densidad, sino sólo la fluctuación de la densidad a lo largo de la pieza moldeada con respecto al valor medio. Por esta razón, la desviación estándar de la densidad en cada paso temporal de la fase de enfriamiento, así como la temperatura media de la superficie de la pieza moldeada en el momento del desmoldeo, se utilizan como criterios centrales de evaluación. Esta evolución de la densidad a lo largo del tiempo se muestra en la siguiente figura 2.6.

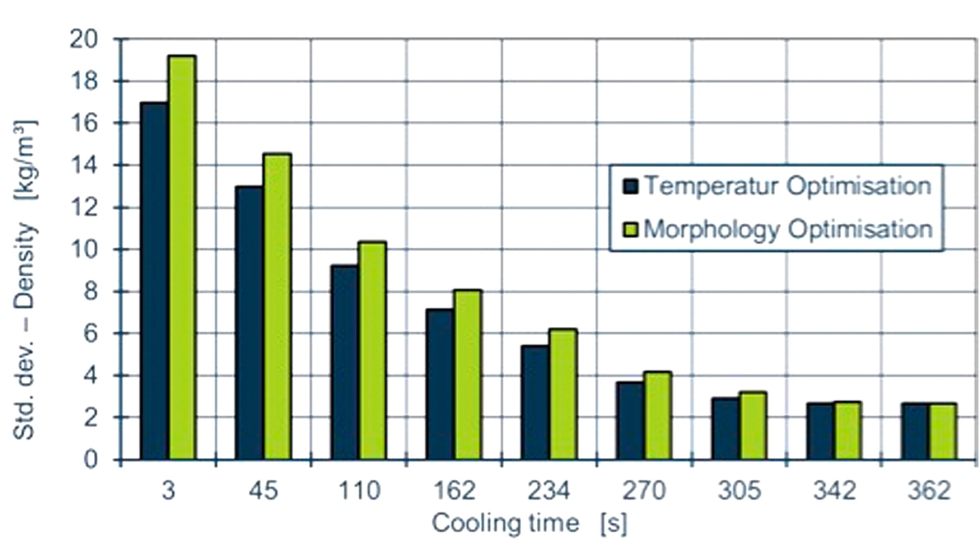
Figura 2.6: Comparación de la desviación típica de la densidad.

Se puede observar que, las diferencias en la desviación de la densidad son muy pequeñas. La fluctuación con respecto al valor global de la densidad se sitúa en torno al 2%. El enfoque dependiente de la temperatura muestra una menor variación de la densidad con el tiempo en comparación con el enfoque morfológico, que se iguala con el tiempo y alcanza una distribución similar al final del enfriamiento. Para poder evaluar claramente la influencia de estas desviaciones estándar de la densidad ligeramente divergentes, en el futuro será aconsejable realizar una simulación y una comparación de la distorsión con las dos disposiciones de canales de refrigeración derivadas.

Los resultados mostrados no son los esperados, ya que las definiciones de las dos funciones de optimización son bastante diferentes. Aunque la evaluación y normalización de la temperatura es similar, se esperaba que la consideración del tiempo de congelación y la velocidad de enfriamiento tuvieran un impacto significativo. La evolución de la temperatura es muy similar. Se puede encontrar una desviación de unos pocos grados, pero no muestra grandes diferencias en la desviación estándar, que es relevante para la calidad de la pieza y el alabeo. El enfoque dependiente de la temperatura tiene un enfoque muy diferente en comparación con el enfoque morfológico. Una razón para que los resultados sean tan similares podría ser la baja conductividad térmica del plástico. La baja conductividad térmica, amplificada por el elevado grosor de la pared, reduce el potencial de optimización, ya que cualquier influencia local de la distribución optimizada de la temperatura se amortigua en el centro de la pieza moldeada. Como el tiempo de enfriamiento es comparativamente largo, una distribución no homogénea de la temperatura en el molde podría igualarse. La temperatura es la característica de calidad determinante en este proceso y tiene una mayor influencia en la función objetivo, lo que conduce a los resultados similares mostrados.

Para el proceso de moldeo por compresión, ambos enfoques conducen a resultados realistas para el diseño térmico inverso del molde. Actualmente, el enfoque dependiente de la temperatura garantiza una variación ligeramente inferior de la densidad y sigue asegurando la consecución de la temperatura final. Por lo tanto, este enfoque es preferible en el caso de geometrías de paredes gruesas. Sin embargo, podrían ser beneficiosos factores de ponderación diferentes debido al elevado grosor de las paredes para lograr mejores resultados con la función de calidad según la ecuación 2.2.

En esta contribución se han probado dos enfoques de optimización diferentes para comprobar su influencia en la calidad de las piezas ópticas moldeadas por compresión. Para calcular correctamente la distribución de la presión, el enfoque térmico de Nikoleizig se amplió a un enfoque termomecánico. El cálculo de las tensiones mecánicas supone un reto para la estabilidad numérica de la optimización. Por ello, se redujo el problema a dos dimensiones.

En futuras investigaciones, deberán estudiarse las interdependencias entre los cálculos térmicos y mecánicos. Actualmente, se utiliza un modelo de material elástico. La masa fundida es muy viscosa, por lo que en el futuro se estudiará un enfoque elastoplástico. Como este enfoque mecánico ampliado añade más complejidad, es necesario controlar de cerca los tiempos de cálculo. Además, se realizarán ensayos prácticos para evaluar la calidad resultante de las piezas producidas. Se compararán con las piezas de la producción en serie de Hella, que se fabrican con un molde convencional. Por un lado, se comprobarán aspectos geométricos como el alabeo de la pieza. Por otro lado, la calidad óptica, como la distribución de la luz, formará parte de la investigación.

La investigación descrita ha sido financiada por la Deutsche Forschungsgemeinschaft (DFG) como parte de los Centros de Investigación Colaborativa CRC 1120. Queremos expresar nuestro agradecimiento a la DFG.

[ALGGS13] Agazzi, A.; Le Goff, R.; Garcia, D.; Sobotka, V.: MCOOL : Optimal cooling system design in injection molding process. Society of Plastics
Engineers (2013), p. 261–264 [ASLG+10] Agazzi, A.; Sobotka, V.; Le Goff, R.; Garcia, D.; Jarny, Y.: A Methodology for the Design of Effective Cooling System in Injection Moulding. International Journal of Material Forming 3 (2010), p. 13–16

[AY07] Au, K. M.; Yu, K. M.: A scaffolding architecture for conformal cooling design in rapid plastic injection moulding. The International Journal of Advanced
Manufacturing Technology 34 (2007), p. 496–515
[AY11] Au, K. M.; Yu, K. M.: A scaffolding architecture for conformal cooling design in rapid plastic injection moulding. Computer-Aided Design 43 (2011)
8, p. 989–1000
[FKP21] Feng, S.; Kamat, A. M.; Pei, Y.: Design and fabrication of conformal cooling channels in molds: Review and progress updates. Applied Thermal
Engineering 171 (2021) 121082,
[HF01] Huang, J.; Fadel, G. M.: Bi-Objective Optimization Design of Heterogeneous Injection Mold Cooling Systems. Journal of Mechanical Design 123
(2001) 2, p. 226–239
[HGH21] Hopmann, C.; Gerads, J.; Hohlweck, T.: Investigation of an inverse thermal injection mould design methodology in dependence of the part geometry.
International Journal of Material Forming 14 (2021) 2, p. 309–321
[HH21] Hohlweck, T.; Hopmann, C.: Thermal Optimisation of Injection Moulds by Solving an Inverse Heat Conduction Problem. Enhanced Material, Parts
Optimization and Process Intensification. Cham, 2021
[HHY16] Hu, P.; He, B.; Ying, L.: Numerical investigation on cooling performance of hot stamping tool with various channel designs. Applied Thermal Engineering
96 (2016), p. 338–351
[HMMM18] Hopmann, C.; Menges, G.; Michaeli, W.; Mohren, P.: Spritzgießwerkzeuge. Mu¨nchen: Hanser, 2018
[Hoh21] Hohlweck, T.: Inverse thermische Optimierung zur wissensbasierten thermischen Spritzgießwerkzeugauslegung. RWTH Aachen, dissertation, 2021
[Hom21] Homberg, A.: Übertragung der Methodik zur inversen Ku¨hlkanalauslegung auf spritzgeprägte Kunststoffoptiken mit Wanddickenspru¨ngen. RWTH
Aachen, Master’s Thesis, 2021 – supervisor: J. Gerads
[HSS18] Hopmann, C.; Schmitz, M.; Schneppe, T.: Digitisation of mould development in precision injection moulding. Internationales Kolloquium Kunststofftechnik. 2018
[HYLH16] He, B.; Ying, L.; Li, X.; Hu, P.: Optimal design of longitudinal conformal cooling channels in hot stamping tools. Applied Thermal Engineering 106
(2016), p. 1176–1189
[LDC+07] Lin, Y. J.; Dias, P.; Chum, S.; Hiltner, A.; Baer, E.: Surface roughness and light transmission of biaxially oriented polypropylene films. Polymer
Engineering Science 47 (2007) 10, p. 1658–1665
[LLLH12] Li, C. G.; Li, C. L.; Liu, Y.; Huang, Y.: A new C-space method to automate the layout design of injection mould cooling system. Computer-Aided
Design 44 (2012) 9, p. 811–823 327
[LLM05] Li, C. L.; Li, C. G.; Mok, A.: Automatic layout design of plastic injection mould cooling system. Computer-Aided Design 37 (2005) 7, p. 645–662
[LMLX16] Li, H.; Mei, Y.; Lin, B.; Xiao, H. Q.: Design and Optimization of Conformal Cooling System of an Injection Molding Chimney. Materials Science Forum 850 (2016), p. 679–686
[MHMS14] Menges, G.; Haberstroh, E.; Michaeli, W.; Schmachtenberg, E.: Menges Werkstoffkunde Kunststoffe. Mu¨nchen: Carl Hanser Fachbuchverlag, 2014
[Nik18] Nikoleizig, P.: Inverse thermische Spritzgießwerkzeugauslegung auf Basis des lokalen Ku¨hlbedarfs. RWTH Aachen, dissertation, 2018 – supervisor: C.
Hopmann
[Shi19] Shin, K.-H.: A method for representation and analysis of conformal cooling channels in molds made of functionally graded tool steel/Cu materials. Journal
of Mechanical Science and Technology 33 (2019) 4, p. 1743–1750
[SHR+19] Schmitz, M.; Hopmann, C.; Röbig, M.; Pelzer, L.; Topmöller, B.; Wurzbacher, S.: Jenseits menschlicher Fähigkeiten. Kunststoffe 109 (2019), p. 142–145
[WYW15] Wang, Y.; Yu, K.-M.; Wang, C. C.: Spiral and conformal cooling in plastic injection molding. Computer-Aided Design 63 (2015), p. 1–11