Modelización de tratamientos térmicos en envases plásticos

*CITA La Rioja, Centro Innovación y Tecnología Alimentaria de La Rioja.

** Departamento de Tecnología de Alimentos Universidad Pública de Navarra.

La problemática de la simulación del procesado térmico de los alimentos se complicará a la vez que lo haga la geometría del envase, aunque como siempre la determinación de la evolución de la temperatura en cada punto de la masa del producto deberá establecerse de acuerdo con el mecanismo de transmisión que tenga lugar en cada caso: conducción, convección.

El empleo de modelos matemáticos para simular los tratamientos térmicos de alimentos envasados es hoy una práctica generalizada gracias al uso de ordenadores cuya potencia permite realizar los cálculos necesarios en tiempo real. C.O. Ball (1923 y 1928) fue el primero en abordar el estudio de la penetración de calor por métodos matemáticos para la predicción de la combinación tiempo-temperatura partir de datos experimentales. De aquellos estudios Ball dedujo que la temperatura en centro geométrico de una lata de conserva tiende hacia la temperatura del recinto del autoclave de forma logarítmica. Numerosas variaciones del modelo desarrollado por Ball en los años 20 están disponibles con diversas puntualizaciones en la precisión.

Cuando la transmisión de calor se produce por un mecanismo de conducción será interesante la utilización de soluciones numéricas por diferencias finitas al método de Fourier en el caso de que se utilicen formatos regulares de envase: esferas, cilindros o paralelepípedos. Sin embargo, cuando los envases tengan formas menos regulares (que sería el caso de los envases plásticos) será necesario definir las condiciones de contorno mediante un análisis de elementos finitos, cuya metodología de resolución de numérica es más compleja que la empleada para las diferencias finitas. (Tucker, 1991).

La utilización de productos naturales en la validación de los modelos obtenidos presenta dificultades añadidas. En primer lugar se debería tener en cuenta la variabilidad natural de sus propiedades termofísicas y además que estos productos no permiten más que una sola utilización, ya que el tratamiento térmico modifica sus propiedades físicas y por ello su respuesta al próximo calentamiento. Por ello, a lo largo de las últimas décadas se ha venido trabajando con distintos productos para la simulación de alimentos.

En el presente estudio se empleó para la simulación de alimentos silicona fluida envasada en barquetas de material PP-EVOH-PP utilizado para el envasado de platos preparados (Fig. 1). Los tratamientos térmicos se han realizado en un autoclave de planta piloto Surdry, trabajando con duchas de agua sobrecalentada (Fig.2).

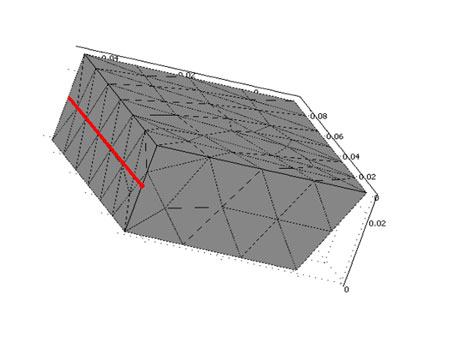
En la construcción del modelo de simulación en la geometría de la barqueta se definió un modelo trapezoidal tridimensional en el que quedaba representado el mallado de un cuadrante del volumen definido para la barqueta, representándose también la situación del punto en el que se ha calculado la temperatura (centro térmico). (Fig.3).

Se consideraron condiciones de contorno convectivas para el exterior y conductivas para el interior, estos datos se introdujeron en el paquete COMSOL Multiphysics donde se simuló el tratamiento térmico.

En el modelo se asumió:

1) El simulante de producto, de propiedades térmicas conocidas, las mantiene constantes a lo largo de todo el proceso térmico.

2) La figura presenta dos planos de simetría, por lo que la simulación se plantea sobre un cuarto de su volumen.

3) Los valores de coeficiente de película (h) en la superficie externa se considerarán constantes o función de la temperatura del recinto.

4) Condiciones de subdominio: se asume que comportamiento de la silicona es por conducción dada su alta viscosidad.

5) Condiciones de contorno: como se trata de un cuarto de barqueta, existen caras que se encuentran aisladas (las correspondientes a los planos de simetría) y caras sometidas a flujo de calor convectivo (las correspondientes a la superficie de la barqueta).

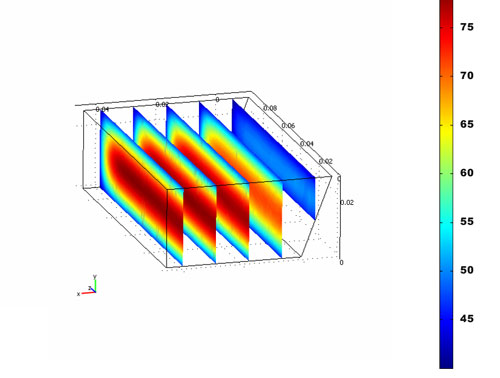
Para obtener estos perfiles de temperatura representados en la figura 4 se ha optimizó la función que representa la penetración de calor en el sistema tomando como variable el valor del coeficiente de película y ajustándolo hasta conseguir minimizar el error cometido en la simulación.

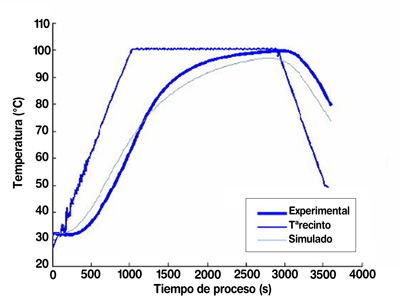
1. Mantener constante el valor del coeficiente de película a lo largo de todo el procesado térmico. (Fig.5).

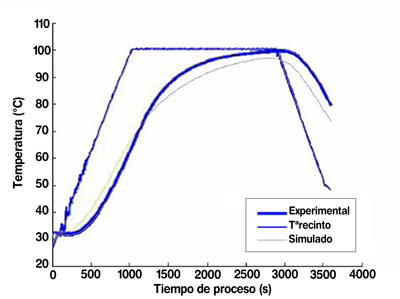
2. Hacer que el coeficiente de película sea función de la temperatura del recinto. (Fig.6).

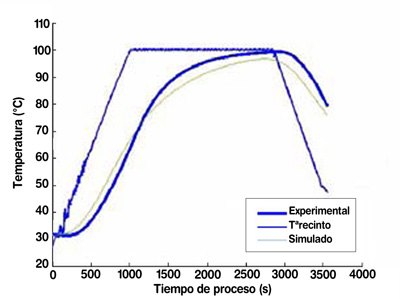
3. Optimizar el ajuste del supuesto 2 para la fase de mantenimiento, que es cuando se produce la mayor cuenta de F0 del proceso (Fig. 7.).

En todos los casos el error se ha calculado a través de la aplicación matemática Matlab.

La utilización de modelos que asumen que el coeficiente de película exterior se mantiene constante durante el tratamiento térmico lleva a cometer errores excesivamente grandes. Para minimizar estos errores es necesario considerar que el coeficiente de película es función de la temperatura del medio de calefacción lo que complica el cálculo a la vez que se acerca a la realidad.

El modelo establecido de esta forma es capaz de simular el comportamiento térmico de las barquetas llenas de silicona de alta viscosidad con un error razonablemente pequeño. Para reducir este error se deberá tener en cuenta que, aunque la viscosidad de la silicona empleada sea muy alta, se producen corrientes de convección en el interior de la barqueta que consiguen que la transmisión de calor no pueda considerarse como puramente conductiva.