Simulación del proceso de flowforming aplicado a llantas
21 de julio de 2010
Uno de ellos es el proceso de flowforming, una potente tecnología que permite adelgazar zonas no críticas de las llantas con el objetivo de reducir peso. Hay que tener en cuenta que las cinco ruedas del coche representan cerca del 3% del peso neto del vehículo, por lo que son piezas que deberían ser optimizadas en términos de peso, considerando también que influyen directamente en el manejo del coche y en el confort a la hora de conducirlo. Además, la llanta representa el 50% del peso total de la rueda y solamente algunas zonas de la llanta requieren grandes espesores, por lo que la combinación del proceso de flowforming con aceros de alta resistencia puede llevar a una reducción significativa del peso de las ruedas.
En el artículo se muestran dos aproximaciones diferentes al problema de simular los procesos de flowforming para llantas en aceros de alta resistencia. El primero ha sido desarrollado en Abaqus/Explicit y tiene en cuenta casi todos los parámetros del proceso. El segundo es un modelo simplificado, donde únicamente una pequeña porción de la llanta es simulada con Abaqus/Standard para comprobar el diferente comportamiento de las zonas interiores y exteriores de la llanta.
Los resultados de deformación son comparados con los resultados experimentales, medidos por un sistema óptico. La comparación muestra que hay un buen acuerdo entre ellos.
El proceso de flowforming
El proceso de flowforming se lleva a cabo mediante la aplicación de una carga de compresión uniforme sobre el diámetro externo de un componente cilíndrico usando para ello una combinación de fuerzas axiales y radiales realizadas por tres o cuatro rulinas controladas mediante CNC. Durante el proceso las rulinas rotan como el mandrino interno contra el que el tubo es colocado. Según las rulinas avanzan a lo largo de la dirección axial, el material es comprimido y deformado por encima de su límite elástico y fluye a lo largo de la dirección axial del tubo [1].
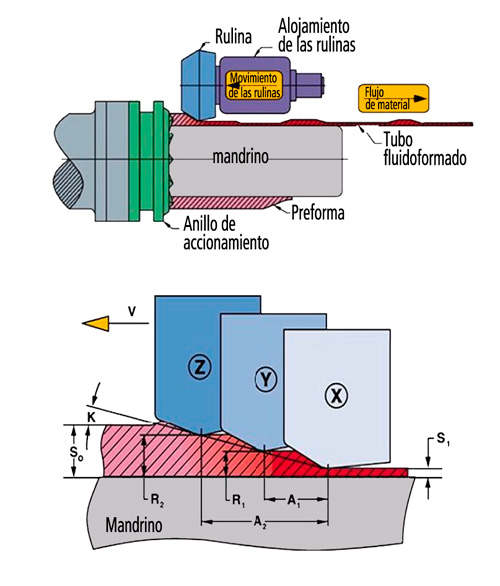
Las rulinas están decaladas axial y radialmente entre sí para equilibrar el peso del tubo y minimizar las fuerzas de conformado.
Modelo de elementos finitas
El método típico para optimizar los procesos de flowforming es el de prueba y error, que conlleva tiempos muy largos en los procesos de puesta a punto. Una forma de conseguir un mejor conocimiento del proceso es desarrollar modelos de simulación numérica por elementos finitos. Estos modelos sirven también como herramientas predictivas para diseñar y optimizar los procesos de flowforming.
Se han desarrollado dos modelos diferentes para obtener resultados de deformaciones y poder compararlos con los obtenidos de forma experimental. El primer modelo, llamado modelo real, trata de representar el caso experimental completo teniendo en cuenta casi todos los parámetros de proceso (geometría de las rutinas, velocidad de avance, gap entre llanta y mandrino..) El segundo, llamado modelo plano, es un modelo simplificado que representa un pequeño trozo de llanta que se considera plana.
Caso de estudio
El proceso de flowforming de llanta seleccionado tienen las siguientes características:
- Longitud llanta = 212 mm
- Diámetro interno llanta = 388 mm
- Espesor inicial llanta = 2.6 mm
- Velocidad de rotación = 800 rpm
- Velocidad de las rulinas = 550 mm/min
- Diámetro rulina = 60 mm
- Distancia entre llanta y mandrino = 0.2 mm

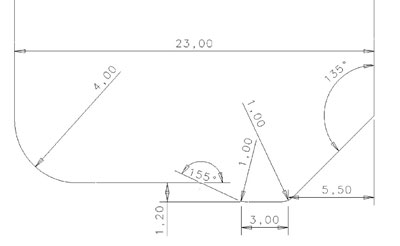
La geometría de la rulina juega un papel muy importante en el proceso de flowforming. En este caso, las tres rutinas tienen la misma geometría, que tiene como zona más importante un parte plana de 3mm de longitud.
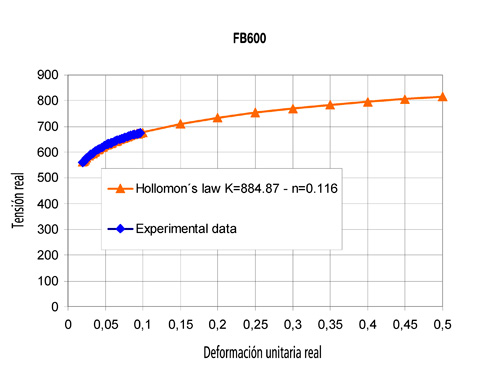
La llanta está hecha con acero de alta resistencia HR60, también conocido como FB600. Los datos experimentales de tensión-deformación se ajustaron a la ley de Hollomon
σ= Kεn
(1)
con K = 884.87; n = 0.116
Modelo real
El primer modelo fué hecho con Abaqus/Explicit. Las rulinas y el mandrino se modelizaron como cuerpos rígidos (elementos R3D4) y la llanta se modelizó con elementos C3D8R.
Durante el proceso, las rulinas, según se mueven en la dirección axial rotan también sobre su propio eje debido a las fuerzas de fricción que aparecen entre la llanta y las rulinas. Por tanto, el grado de libertad de las rulinas que corresponde con la rotación alrededor de sus propios ejes no tiene ninguna condición previa para permitir que el material de la llanta ya deformado fluya en la dirección axial.

Para validar los resultados de la simulación, algunas llantas fueron marcadas en su superficie con una malla por electrodeposición, de manera que pudiese medirse las deformaciones principales mediante el sistema óptico de análisis de deformaciones ASAME (Automated Strain Analysis and Measurement Environment). Las llantas seleccionadas para ser medidas tienen una reducción de espesor del 40%, es decir, que su espesor pasa de 2,6 a 1,56 milímetros.
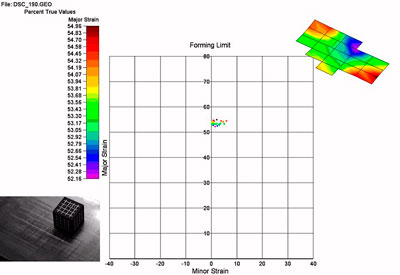
Para obtener los resultados de deformación no es necesario realizar la simulación completa del proceso, ya que las deformaciones del material deformado alcanzan un nivel estacionario en un tiempo determinado. En ese punto, los resultados obtenidos por simulación muestran un buen acuerdo con los obtenidos experimentalmente.
Tabla 1: Resultados de deformación experimental vs. resultados de deformación numéricos
| Deformación principal máxima | Deformación principal mínima | |
| Exp. | 52-55% | 3-4% |
| Sim. | 47-50% | 1-2% |
Como en los modelos explícitos el tiempo de cálculo depende directamente del tamaño mínimo del elemento más pequeño [1], solamente se pusieron dos elementos en el espesor de la llanta, por lo que no es posible observar diferencias entre las superficies interna y externa de la llanta. Para obtener esa información, se desarrolló otro modelo.
Modelo plano
El modelo plano es un modelo simplificado que solo tiene en cuenta una pequeña porción de la llanta.. Esta porción tiene un tamaño de 100 x 100 x 2,6 mm.
Para evitar el problema del tiempo de cálculo debido al tamaño de los elementos, se usó Abaqus/Standard. En este caso, no hay mandrino y las rutinas son consideradas rígidas con elementos R3D4, mientras que la llanta se modeliza con elementos C3D8.
Para tener en cuenta la presencia del mandrino, los nodos en la superficie interna de la llanta están constreñidos en sus posiciones iniciales en la dirección radial. Asimismo, los nodos de tres de los cuatro lados de la llanta están fijos. Únicamente los nodos de uno de los lados tienen la posibilidad de moverse para permitir al material fluir en la dirección axial. En este modelo, solo se han simulado nueve pasadas de la rulina sobre la llanta.
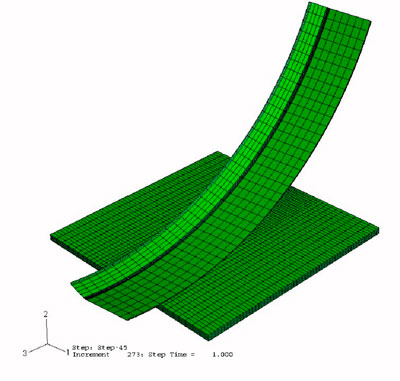
Para hacer una comparación adecuada, se estableció la relación entre las direcciones del modelo real y las del modelo plano.
Tabla 2: Relación entre las direcciones del modelo real y las del modelo plano
| Modelo real | Modelo plano |
| Dirección axial | Dirección 1 |
| Dirección radial | Dirección 2 |
| Dirección circular | Dirección 3 |
Se colocaron seis elementos en el espesor de la llanta para poder observar las diferencias entre las superficies interna y externa de la llanta. Se simuló un caso de reducción del 30% para evaluar estas diferencias y comparar los resultados del modelo plano con los del modelo real.
Tabla 3: Comparación entre el modelo real y el modelo plano para un caso de reducción del 30%
| 30% reducción | Modelo real | Modelo plano | Modelo plano |
| Deformaciones plásticas | - | Cara externa | Cara interna |
| Mayor (mayor en plano) | 32-35% | 36-40% | 30-32% |
| Media (menor en plano) | 1-2% | 0,5-1% | 0,1-0,2% |
| Menor (espesor) | 33-36% | 37-39% | 31-32% |
| Deformación plástica equivalente | 120-130% | 135-150% | 78-82% |
Como se puede observar en la Tabla 3, los resultados de deformación del modelo real están entre os resultados obtenidos par alas superficies interna y externa de la llanta en el modelo plano, debido a la menor definición que posee el espesor en el modelo real. Pero el acuerdo entre ambos modelos, en términos de deformación es bastante bueno.
Para comprender mejor por qué la deformación plástica equivalente alcanza valores tan altos mientras las deformaciones principales tienen valores mucho más bajos, se representó la evolución de las deformaciones plásticas durante el proceso en un elemento (9570) situado en la superficie externa de la llanta y aproximadamente en el centro de la porción modelizada de la llanta.
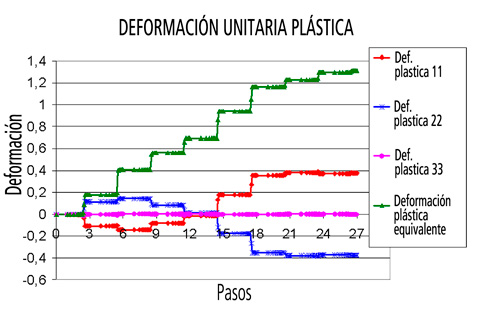
Como el caso se corrió en un código implícito (Abaqus/Standard) el tiempo no es tenido en cuenta de forma directa. Por tanto, en la Figura 9, los valores de en la abscisa no son valores temporales; representan el número de pasos en los que está dividida la simulación. Cada pasada de la rulina está dividida en 3 pasos de simulación; los dos primeros son para colocar la rulina en su posición y el tercero es el paso en el que la rulina deforma la llanta, de manera que la deformación se produce entre los puntos 2-3, 5-6, 8-9, 11-12, 14-15, 17-18, 20-21, 23-24 y 26-27 de la figura 9.
Para las direcciones axial (dirección 1) y radial (dirección 2) hay una inversión del sentido de los valores de deformación, pasando de valores de tensión a valores de compresión en la componente axial y viceversa para la componente radial. La razón es la acumulación de material en frente de la rulina antes de que esta pase sobre el mismo. Según el material es comprimido, los elementos pasan a un estado de compresión en la dirección axial y a un estado de tracción en la dirección radial, debido a que se debe conservar el volumen del elemento y no hay deformación en la dirección circular debido a las restricciones del modelo. (Figuras 10 y 11).
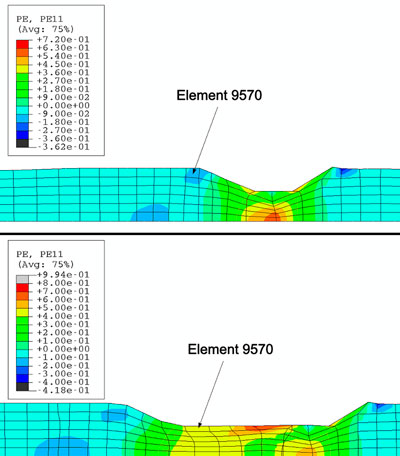
Después de que la rulina pase sobre el elemento, su estado de deformación cambia, debido a que se reduce el espesor del elemento, de tal manera que la componente radial pasa a un estado de compresión, mientras que la componente axial se deforma hasta alcanzar un estado de tensión. (Figuras 12 y 13).
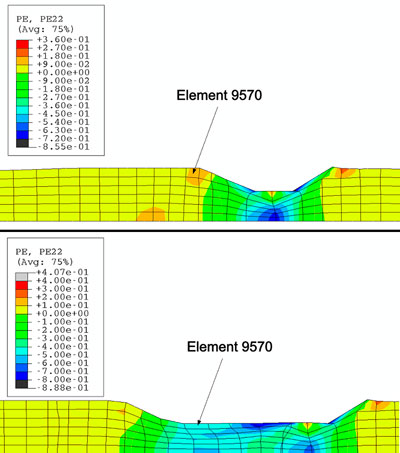
El valor de deformación plástica equivalente es un valor acumulado a lo largo de todo el proceso:
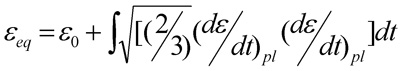
siendo (dε/dt)pl las componentes del tensor de velocidades de deformación, de manera que el cambio en el signo en las deformaciones radiales y axiales no tiene influencia in su valor final. Depende de cómo sea el camino de deformación y no de los valores puntuales de las deformaciones principales.
Para el modelo real, también se representó la evolución de las deformaciones durante el proceso para un elemento localizado en el centro de la llanta.
El comportamiento es bastante similar al que se mostró en el modelo plano. Las deformaciones axiales cambian su signo durante el proceso como en el modelo plano y lo mismo ocurre con las deformaciones radiales, pero para estas hay una oscilación durante el resto del proceso que afecta también a las deformaciones circulares. Esto podría ser un efecto numérico debido a la rotación del material. Para la deformación plástica equivalente, hay, como en el modelo plano un rápido incremento de su valor según los elementos son deformados. Después de eso, el valor de deformación plástica equivalente tiende a estabilizarse.
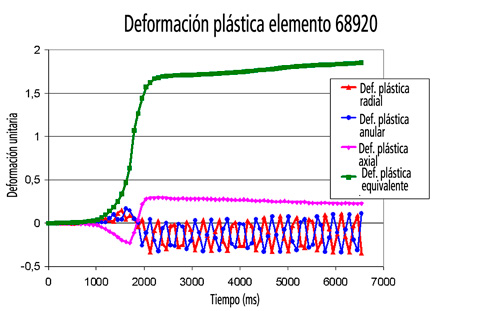
Los dos modelos muestran comportamientos y valores similares par alas deformaciones plásticas principales y la deformación plástica equivalente, de manera que ambos se pueden usar para modelizar el proceso de flowforming.
Conclusiones
El proceso de flowforming de llantas de aceros de alto límite elástico puede ser un proceso interesante para reducir el peso del vehículo. Para entender como los parámetros de proceso afectan a los resultados de deformación se han desarrollado dos modelos de simulación. El primero, llamado modelo real, se desarrolló con Abaqus/Explicit y representa el modelo completo teniendo en cuenta casi todos los parámetros del proceso. El segundo, llamado modelo plano, se desarrolló con Abaqus/Standard y representa solamente nueve pasadas de las rulinas sobre una pequeña porción de la llanta.
Por un lado, los resultados de deformación del primer modelo fueron comparados con los obtenidos experimentalmente sobre una llanta real con un sistema óptico de medida. La comparación mostró un excelente acuerdo entre los resultados de simulación y los experimentales. Por otro lado, se compararon los resultados de deformación de los dos modelos entre sí, mostrando de nuevo un buen acuerdo. Por tanto, los dos modelos se pueden usar para estudiar el problema de deformación de las llantas por medio de flowforming.
Trabajos futuros
Un mejor conocimiento del proceso de flowforming y, en particular, de la influencia de los parámetros de proceso en las propiedades mecánicas y geométricas de la pieza final, obtenido mediante simulación se revela como un elemento fundamental para los técnicos de diseño de proceso. De hecho, es posible reducir los tiempos de diseño y puesta a punto, conocidas las especificaciones del producto en cuanto a su resistencia estructural. Además el conocimiento de las posibilidades y restricciones de la tecnología de flowforming sirve como apoyo al diseño de nuevos productos.
Agradecimientos
Este trabajo se ha desarrollado en el marco del proyecto CECA “Influencia de los parámetros del proceso de flowforming sobre el comportamiento a fatiga de ruedas de alto límite elástico para el sector de automoción”. El proyecto ha sido ejecutado en cooperación con CSM (Italia), Magnetto Wheels (Italia), Arcelor-Automotive Application Research Center (Francia), LABEIN-Tecnalia (España) y Arcelor-IRSID (Francia). Se agradecen especialmente los fondos aportados por la Comunidad Europea.
Referencias
[1] Metals Handbook (Vol.14; Pag. 317). ASM (American Society for Metals) Editions, 1978.
[2] Abaqus Analysis User's Manual (version 6.6). Abaqus Inc., 2006.
































