Modelo cinemático de diamantado con disco
1. Enfoque/aplicación/problemática industrial
1.1. Contextualización del trabajo
Cuando un eje está girando la mayoría de las ocasiones montará un rodamiento solidario a dicho eje para lograr una transmisión del movimiento más suave y efectivo. Normalmente, acompañando a dicho eje y rodamiento estarán los sellos. De una manera breve, el sello funciona como una barrera y sus funciones pueden ser:
- Evitar fugas o el intercambio no deseado de fluidos o sólidos.
- Mantener la presión de un lado del sello respecto al otro.
- Evitar la introducción de suciedad, partículas o contaminantes.
- Separar fluidos entre ambos lados del sello.
Para lograr un funcionamiento óptimo del sistema de sellado, se exige un diseño estricto del sistema y una fabricación precisa de todo el conjunto: eje rotativo, sello radial y rodamiento (Figura 1).
![Ilustración 1: a) ejemplo de un sello radial; b) Disposición de un sello radial sobre un eje rotativo. [www.fts.com] Ilustración 1: a) ejemplo de un sello radial; b) Disposición de un sello radial sobre un eje rotativo. [www.fts.com]](https://img.interempresas.net/fotos/1606091.jpeg)
Aunque el sello esté diseñado y seleccionado de una manera óptima para una determinada aplicación, un fallo en el montaje del retén puede originar funcionamientos no deseados. Un montaje correcto de un retén dependerá fundamentalmente de las características del eje sobre el que se instalará el sello radial:
- Una alta dureza superficial (30HRC como mínimo). Una rugosidad superficial del eje en un rango controlado. (según la norma DIN 3760 y 3761)
? Ra entre 0,25 µm y 0,50 µmRz entre 0,5 µm y 5 µm y Rmax < 6,5 µm.
- Ausencia de posibles patrones helicoidales originados en el mecanizado (según la norma interna de Daimler [MBN, 2008], las tolerancias de los surcos helicoidales generalmente son 0 +/- 0,05º en ángulo y 0,3 mm en profundidad).
![Ilustración 2: Parámetros del diamantado y la generación de surcos helicoidales sobre la superficie de la muela en el diamantado [San. 2011]... Ilustración 2: Parámetros del diamantado y la generación de surcos helicoidales sobre la superficie de la muela en el diamantado [San. 2011]...](https://img.interempresas.net/fotos/1606092.jpeg)
Existen múltiples posibilidades y procesos de fabricación que permiten lograr los requerimientos mencionados en los ejes rotativos. Sin embargo, el más recomendado y el más extendido por la industria es el rectificado cilíndrico en penetración.
En comparación con los procesos de mecanizado convencionales, el hecho de que una muela rectificadora no tenga un filo de corte definido en su superficie activa, resulta beneficioso a la hora de evitar generar un surco en helicoidal sobre el eje a rectificar.
Sin embargo, el proceso de rectificado en penetración no es suficiente para asegurar la ausencia de dichos patrones (en inglés ‘no-lead’) sobre la superficie de la pieza. En ocasiones, bajo ciertas condiciones de diamantado y rectificado, y aunque la pieza final cumpla todos y cada uno de los requisitos tanto de la rugosidad superficial como de las tolerancias dimensionales, aparecen patrones helicoidales sobre la periferia del eje.
![Ilustración 3: Patrón helicoidal en la superficie del eje rectificado. [taylor-hobson.com] Ilustración 3: Patrón helicoidal en la superficie del eje rectificado. [taylor-hobson.com]](https://img.interempresas.net/fotos/1606093.jpeg)
Distintos autores [Kun. 2016; Bau. 2013; See. 2009], asocian la generación del surco a la operación del diamantado. Según estos autores, el propio proceso de diamantado deja los patrones helicoidales en la superficie de la muela y ésta, bajo ciertas condiciones de rectificado, los traslada o reproduce en mayor o menor medida sobre la superficie rectificada. Partiendo de esta hipótesis Shubert [Shu. 2013] utiliza una expresión matemática compacta (ec. 1) para determinar el ángulo de la hélice resultante de una operación de torneado. Realizando la analogía del proceso de torneado para el caso de diamantado, y asumiendo la hipótesis de que el patrón helicoidal que aparece en las piezas rectificadas tiene como origen los surcos que quedan en la muela tras el diamantado, el ángulo del hilo teórico sobre la muela obedecería también a la ecuación 1:
![Ilustración 4: trayectoria helicoidal de los surcos sobre la superficie abatida de una la muela [Cho. 2013] Ilustración 4: trayectoria helicoidal de los surcos sobre la superficie abatida de una la muela [Cho. 2013]](https://img.interempresas.net/fotos/1606094.jpeg)
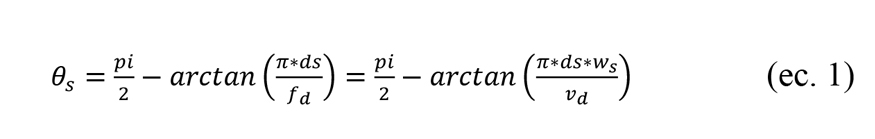
Si bien este tipo de trabajos son interesantes desde un punto de vista cualitativo, lo cierto es que asumen hipótesis simplificativas que limitan su validez (como por ejemplo que la superficie de la muela es plana) (ilustración 4).
Por ello, resulta necesario un análisis más profundo y una validación experimental de la influencia del diamantado sobre la topografía de muela que justifiquen las características de los surcos helicoidales en función de los parámetros de diamantado y en función de las características de una muela determinada.
A nivel industrial, los fabricantes de las aplicaciones de sellado recomiendan utilizar una ratio de velocidades no entero en el proceso de rectificado por penetración (tanto para el rectificado como para el diamantado), así como largos tiempos de apagado de chispa [Vog. 2014]. La ratio de velocidades angulares no entero tiene como propósito evitar el solapamiento de trayectorias sucesivas en el proceso de rectificado. El apagado de chispa reducir la rugosidad superficial de la pieza final.
Por otro lado, no existe un protocolo de medición de los patrones helicoidales aceptado de manera universal a nivel industrial. Es por ello que resulta difícil cuantificar los parámetros característicos de la hélice. En esta línea Nagy et al. [Nag. 2016] han realizado ensayos bajo distintas condiciones de rectificado y han llegado a concluir que aumentando en apagado de chispa de 2 vueltas a 6, el desplazamiento del hilo en el ensayo de medición de la hélice se reduce más de un 80%. Sin embargo, en este trabajo no se han tenido en cuenta las condiciones de diamantado y no se ha realizado ninguna comparativa en qué porcentaje puede afectar el diamantado en el resultado de la generación del hilo. Tampoco han evaluado cómo influye el utilizar distintos tipos de muela en el estudio.
Así, resulta evidente que existe cierto interés industrial y a la vez científico en analizar bajo qué condiciones de diamantado se generan en la muela unos surcos helicoidales que puedan ser copiados sobre la pieza en operaciones de rectificado.
Asumiendo que el origen de la hélice es el proceso diamantado, que éste genera unos surcos helicoidales sobre la muela, y estas bajo ciertas condiciones de rectificado se copian sobre la pieza, en este trabajo se presenta un modelo cinemático de diamantado en 3D con el que se permitirá estudiar aspectos topográficos de las diferentes muelas tras las operaciones de diamantado.
El objetivo de dicho modelo es predecir las características del surco helicoidal generado sobre la superficie activa de la muela bajo diferentes parámetros de diamantado, para poder caracterizar después la reproducción de dichas marcas en las piezas tras operaciones de rectificado en penetración.
1.2. Revisión de los modelos de diamantado
Múltiples autores han tratado de caracterizar la operación del diamantado y predecir la topografía de la muela tras su diamantado correspondiente. Realizando un breve repaso cronológico de las más importantes, los que primero intentaron de caracterizar el proceso de diamantado fueron Pahlitzsch et al. [Pah. 1954], haciendo una analogía al proceso de torneado sobre la muela. Los autores consideraron que el resultado de la operación de diamantado era un surco helicoidal provocado por la trayectoria del diamantador monopunta. Más tarde, se ha puesto en duda dicha afirmación poniendo de manifiesto la fractura frágil de los abrasivos y la fractura del material aglutinante de la muela, que hacen que los granos abrasivos sobre la superficie de muela se desprendan. Por ello, hoy en día se asume que los efectos de torneado (fractura dúctil) y el astillado (fractura frágil) se combinan en el proceso de diamantado [Mal. 2008]. En la siguiente ilustración se observan los tipos de desgaste de abrasivo que se pueden dar en las operaciones de diamantado que se resumen en fractura dúctil de los abrasivos, la fractura frágil y el desprendimiento de granos abrasivos o la rotura del aglomerante:
![Ilustración 5: Tipos de desgaste del abrasivo en el proceso de diamantado. Modificado de [Mar.2004] Ilustración 5: Tipos de desgaste del abrasivo en el proceso de diamantado. Modificado de [Mar.2004]](https://img.interempresas.net/fotos/1606096.jpeg)
Brinksmeier y Cinar [Bri. 1995] caracterizaron el proceso de diamantado estimando el número de colisiones entre el diamantador y los granos abrasivos. A su vez, Chen y Rowe [Chen 1996] propusieron que en el caso del diamantado monopunta el porcentaje de fractura frágil es proporcional al área de intersección entre la trayectoria de la punta del diamantado y los granos abrasivos. El principal contrapunto de este modelo reside en la aplicabilidad del mismo porque requiere una serie de ensayos de caracterización para tipología de muela o diamantador.
Más tarde, Koshy et al. [Kos. 1997] desarrollaron un modelo de diamantado monopunta para muelas de diamante que calculaba estadísticamente la altura media de los granos sobre la superficie de la muela.
Ya en 2008, considerando la importancia industrial del diamantado rotativo Baseri [Bas. 2008] desarrolla un modelo de diamantado en 2D para los casos de diamantado rotativo con disco electrodepositado de diamante. En la línea de Chen & Rowe, Baseri desarrolla un modelo matemático capaz de asumir el carácter aleatorio en tamaño y espaciado de los granos y considera el área de solapamiento entre diamantador y cada uno de los granos para predecir el grado de fractura dúctil y fractura frágil que se da en el diamantado.
Con la mejora de las posibilidades y capacidades de procesamiento de datos de los ordenadores, estos últimos años han ido apareciendo distintos modelos en 3D que caracterizan la topografía de la muela. También han aparecido modelos 3D de diamantado. Una de ellas ha sido el de Darafon [Dar. 2013], que realizó un modelo de diamantado monopunta, donde modificaba y mejoraba la formulación matemática de Chen y Rowe que predecía el grado de la fractura frágil en base a los parámetros de diamantado.
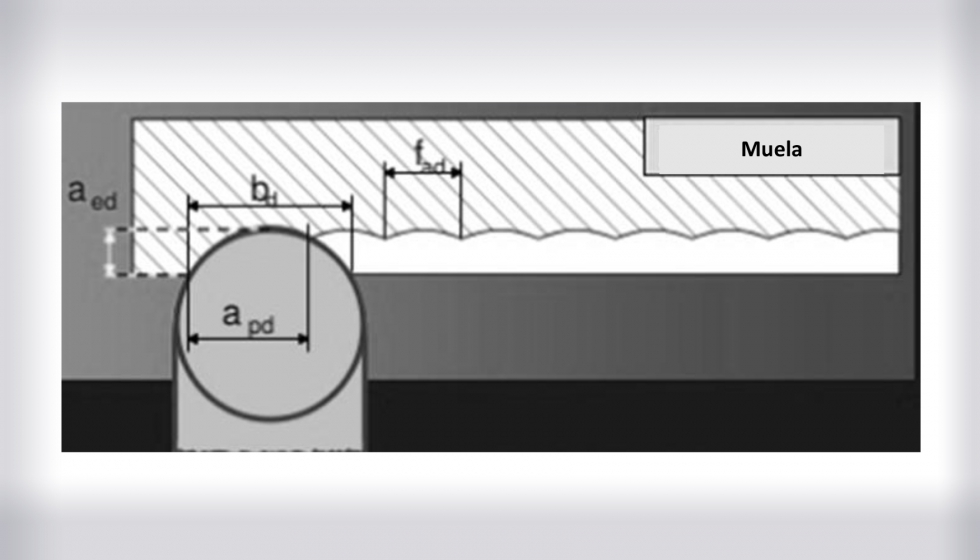
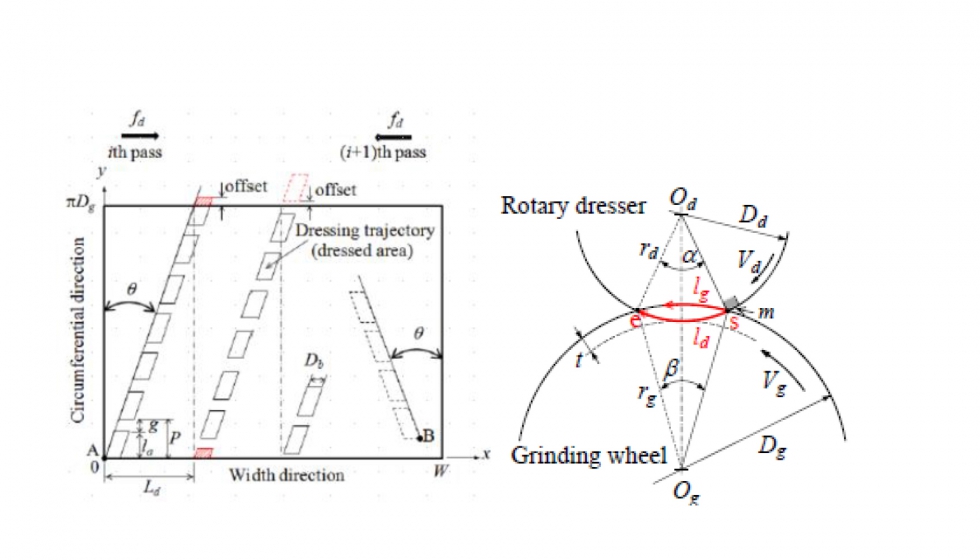
Recientemente, Chowdhury [Cho. 2013] ha desarrollado otro modelo 3D de diamantado para discos infiltrados donde analizaba la eficiencia de diamantado teniendo en cuenta múltiples pasadas de diamantado y concluyendo que para mejorar la eficacia de diamantado hace falta maximizar el área de diamantado y minimizar las áreas de diamantado solapadas entre las diferentes pasadas. El modelo permite la puesta a punto de los parámetros de diamantado como el avance, la profundidad de diamantado o el número de pasadas utilizando la simulación para ello. En cambio, los principales inconvenientes de dicho modelo son que asume una topografía de muela sin granos abrasivos y que sólo resulta válido para los casos de no solapamiento entre las trayectorias de diamantado (Ud< 1[-]) no siendo éstas las condiciones de diamantado fino que requiere el acabado en aplicaciones de sellado. El ratio de solapamiento del diamantado es la relación del ancho de contacto real entre muela y diamantador entre el avance axial del diamantador (ilustración 6).

Este parámetro condicionará el ancho y la profundidad de los surcos generados sobre la muela, y dependerá de los parámetros de diamantado y la geometría que tienen los diamantes sobre el diamantador. Cuando el factor de solapamiento es menor que uno, resulta sinónimo de que no existe solapamiento entre los surcos adyacentes generados por el diamantado en la dirección axial, por lo que todo el perfil del ancho efectivo del diamantador (bef) se copia en la superficie de muela. Sin embargo, reduciendo la velocidad de avance del diamantador el factor de solapamiento del diamantado crece generando unos surcos de menor anchura y profundidad.
Observando en la bibliografía, se puede afirmar que la mayoría de los modelos de diamantado tratan de predecir la densidad de granos estáticos y activos sobre la periferia de la muela y parámetros de rugosidad sobre la muela para posteriormente predecir el comportamiento del rectificado posterior. En esta línea este mismo año, investigadores de la universidad de Kaiserlautern [Set. 2017] han realizado un estudio para predecir el número de filos de corte activos sobre la periferia de la muela teniendo en cuenta la tipología de muela, las condiciones de diamantado, las condiciones de rectificado posterior y también el desgaste del abrasivo a lo largo del rectificado.
Sin embargo, no se ha encontrado ningún modelo que considere y modelice el surco generado en el diamantado y que analice los principales parámetros característicos de la hélice sobre la superficie activa de la muela. Estos parámetros característicos de la hélice están definidos por la norma DIN EN ISO 25175-3:2012-03. De manera resumida se observan en la siguiente ilustración las características principales de la hélice:
![Ilustración 7: Caracterización de los parámetros de la hélice acorde a normas [Shu. 2013] Ilustración 7: Caracterización de los parámetros de la hélice acorde a normas [Shu. 2013]](https://img.interempresas.net/fotos/1606099.jpeg)
Por lo tanto, queda visible la necesidad de ahondar en el conocimiento científico sobre la generación de la hélice y en la búsqueda de los factores que favorecen o desfavorecen la aparición de la misma; como pueden ser la densidad de los filos de corte tras la operación del diamantado, la altura de los filos de corte, los parámetros de diamantado o los mismos parámetros de rectificado.
2. Modelización analítica del proceso de diamantado rotativo por disco infiltrado
2.1. Aspectos generales del modelo
Con la intención de visibilizar la influencia de los parámetros de diamantado en la generación de los surcos helicoidales, se ha desarrollado un modelo cinemático del diamantado rotativo por disco infiltrado que caracterice la topografía de muela tras una operación de diamantado.
Se partirá de la hipótesis simplificativa de que el contacto entre disco diamantador y muela genera únicamente fractura dúctil de los granos, obviando el desprendimiento de grano en las simulaciones del diamantado. Esta simplificación, se hace tomando en consideración que la profundidad de pasada en el diamantado suele ser generalmente muy inferior al tamaño de los granos abrasivos. Para las aplicaciones que se van a analizar, los tamaños de grano recomendados oscilarán entre 190 y 85 µm.
Un fabricante de prestigio como Noritake recomienda unas profundidades de diamantado de 5µm en radio para un rectificado preciso de acabado [Nor, 2014]. En este caso esa profundidad de pasada supone un aproximadamente un 15% del diámetro medio del grano, con lo que la hipótesis de partida se considera adecuada.
Los inputs del modelo serán las características de la muela (el tamaño de grano y su estructura), la geometría del diamantador y los parámetros de diamantado.
Se ha apoyado en el software de Matlab R2010a para realizar el programa de modelización del diamantado. Así, se empezará caracterizando la topografía de muela en base a sus características, seguido de la medición del diamantador y la caracterización de su geometría. Una vez definidas las geometrías del diamantador y en base a los parámetros cinemáticos del diamantado, se evaluará la trayectoria del diamantador produciéndose la fractura de los granos abrasivos que entran en contacto con el disco diamantador.
De esta manera, la salida del modelo será la topografía en 3D de la muela tras la operación de diamantado, el número de filos de corte o granos activos, los perfiles de rugosidad y sus parámetros de rugosidad y el volumen del material arrancado por la operación del diamantado. Todo ello, con el objetivo de caracterizar la superficie de la muela tras los diferentes diamantados y poder predecir los efectos del diamantado y las distintas tipologías de muelas en la generación de la hélice sobre la superficie de la pieza.
2.2. Caracterización de la muela
Como se ha definido en el apartado de aspectos generales, en esta primera caracterización de la muela se pretende conseguir la topografía en 3D de la muela todavía sin diamantar. En concreto, se han establecido como parámetros de entrada al modelo el tamaño de grano (M) y el número de estructura de la muela (S), provenientes de la nomenclatura de las muelas convencionales. Es necesario también recalcar que el modelo se ha desarrollado para muelas convencionales, por lo que la caracterización de muelas superabrasivas queda exenta de esta primera versión del modelo.
En el caso de muelas superabrasivas, la nomenclatura de las mismas varía ya que se indica directamente el diámetro medio de los abrasivos en µm y la concentración (C) de abrasivos en la superficie de la muela. Además las profundidades de diamantado suelen ser mucho menores en caso de muelas superabrasivas, por lo que la modelización de la geometría de los abrasivos tras el diamantado debe ser más precisa en si se quiere mantener la precisión del modelo.
A la hora de modelizar la superficie de la muela se ha asumido que ésta sigue un patrón de rugosidad aleatorio. Tras múltiples intentos de caracterización de la superficie de las muelas, Malkin [Mal 2008] demostró que la distribución de los tamaños de granos se aproximaba a una distribución normal. Con ello, pretendía caracterizar el tamaño de grano de las muelas a partir de un valor nominal y una desviación estándar.
Así, partiendo del tamaño de grano de las muelas estableció que, asumiendo una geometría de granos esféricos, el tamaño medio de los granos abrasivos en la superficie de la muela obedecía a la siguiente ecuación:
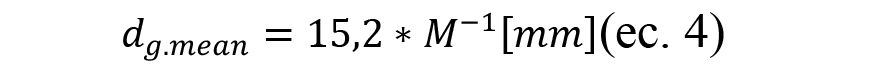
Siendo dg.mean el valor nominal del tamaño de grano y la desviación estándar estará acorde a la siguiente relación [Hou, 2003]:
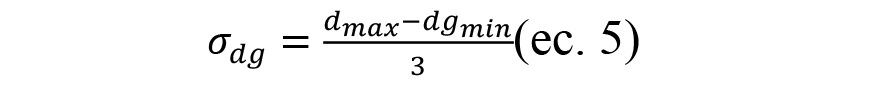
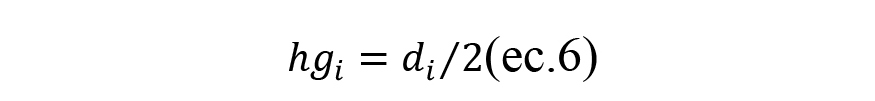
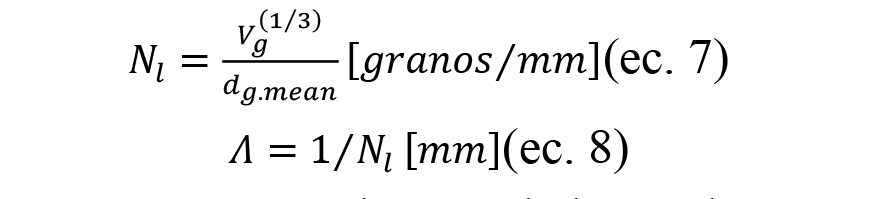
Donde, Vg es la fracción de granos en volumen de la muela y sigue la siguiente relación [Cao 2013]:
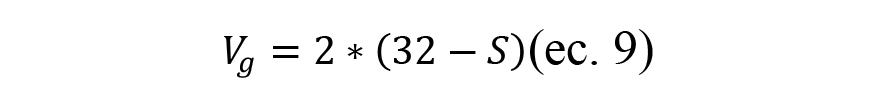
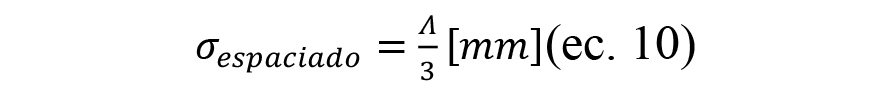
De esta manera, se han definido las posiciones de los centrales de los granos abrasivos a modelizar en coordenadas cartesianas. En cada una de dichas posiciones se ha establecido el tamaño de grano que sigue la distribución normal definida en líneas anteriores. Con el dato del tamaño de grano y su posición central se ha caracterizado la forma esférica de los granos a partir de la ecuación de una esfera de radio hgi=di/2.
Una vez con la distribución de los abrasivos y su geometría ya definida, es importante remarcar que sólo se ha simulado la superficie exterior de la muela. Es decir, para caracterizar el espaciado entre grano y grano se ha considerado una desviación estándar del espaciado medio entre 3, y se ha establecido la condición de no solapamiento entre los abrasivos adyacentes.mulado sólo los abrasivos que sobresalen del material aglutinante de la muela. En el modelo no se simulan ni los puentes aglomerantes ni los poros de una muela típica vitrificada. Se establece una cota radial constante a profundidad del tamaño de grano medio sobre el diámetro exterior de la muela en la que se encuentra el material aglutinante (ver ilustración 7).
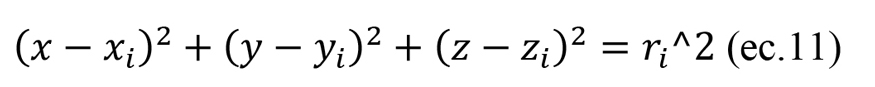
2.3. Caracterización de la geometría del diamantador
Una vez caracterizada la topografía de la muela que será diamantada, el segundo paso consta en introducir al modelo las características geométricas del diamantador.
El modelo presentado en este trabajo se ha centrado en la modelización de los diamantes rotativos infiltrados, donde un número determinado de diamantes de PCD se colocan con espaciado uniforme entre ellos sobre la periferia del disco. Estos diamantes están sujetados por una matriz metálica.
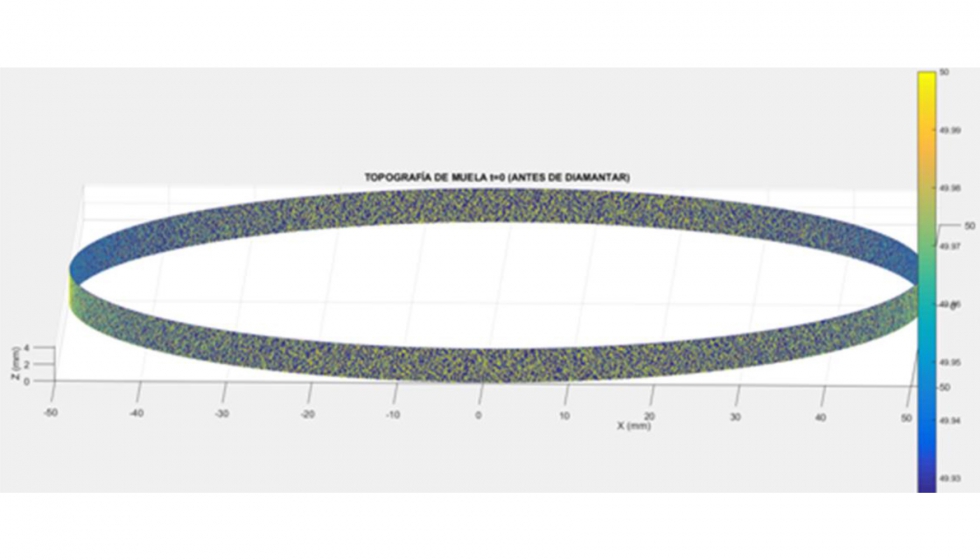
El procedimiento de introducción de la geometría del disco al modelo resulta relativamente sencillo. Primero, se ha medido el perfil exterior de la geometría del diamantador por el microscopio confocal de SensoFar.
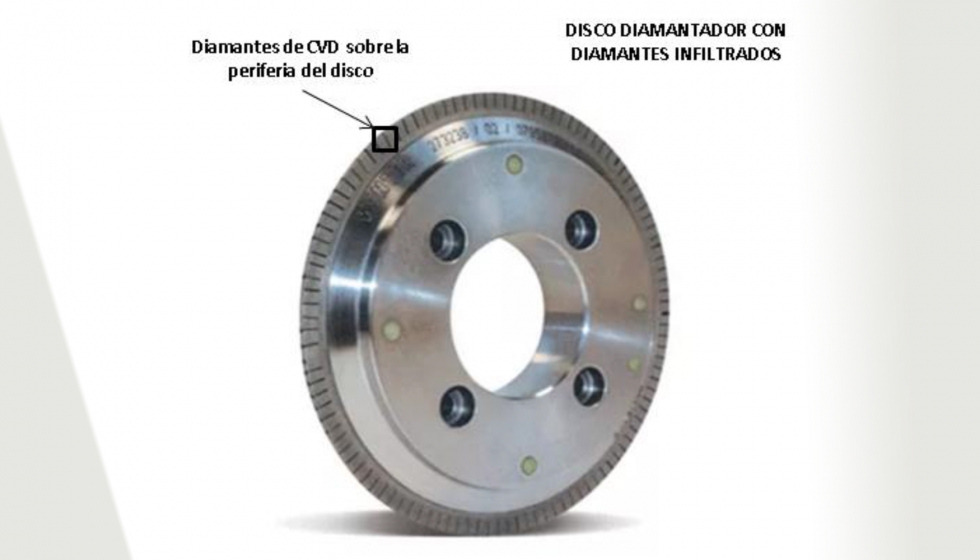
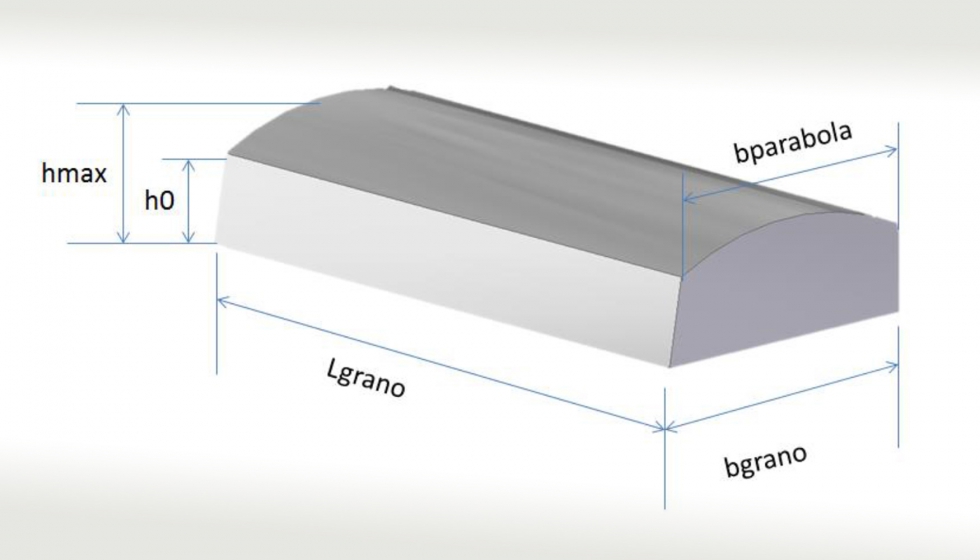
A partir de la obtención de la geometría exterior de la muela, se ha aproximado dicha geometría a un perfil parabólico por un best fit de base trapezoidal de longitud Lgrano (ver ilustración 10), que ha quedado definida por el siguiente sistema de ecuaciones:
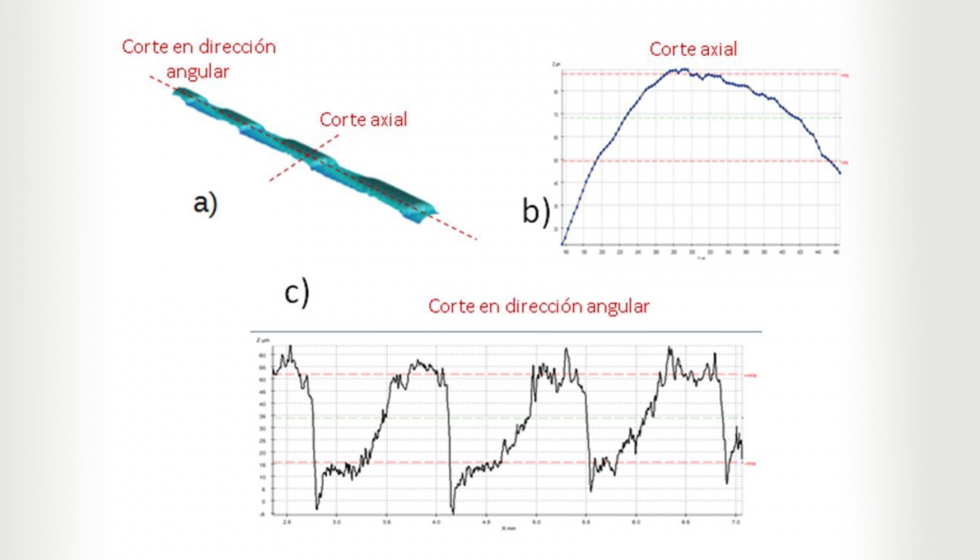
Basándose en las mediciones del confocal y una vez extraídos todos los parámetros definidos en la ilustración 11, considerando el sistema de ecuaciones superior, el perfil que mejor se aproxima a la medición queda reflejado en por la ilustración 12:
2.4. Parámetros de diamantado
Las variables cinemáticas de entrada al modelo serán respectivamente la profundidad de diamantado (ad), la velocidad axial del diamantador (vd), la velocidad de giro de la muela (vs), y la ratio de velocidades periféricas entre diamantador y muela (qd). En base a estos parámetros, se podrán evaluar a continuación las trayectorias del proceso de diamantado y las interacciones entre los diamantes y los abrasivos de la muela.
2.5. Longitud cinemática de la trayectoria del diamantado
A la hora de evaluar el proceso de diamantado por un disco infiltrado, resulta fundamental definir la longitud del surco y el perfil sobre la muela, generado por los diamantes del disco. El contacto entre la muela y diamantador no será permanente debido a que los diamantes del disco infiltrado se encuentran espaciados por una distancia que dependerá del diámetro del disco y el número de diamantes sobre su periferia.
De hecho, dependiendo de las condiciones cinemáticas del diamantado dichos surcos podrían solaparse o no entre ellas. Por ello, partiendo de los parámetros de diamantado, Chowdhury [Cho. 2013] estableció que la longitud de corte en la que los granos de diamante entran en contacto con la superficie de una muela idealizada seguía la siguiente ecuación:
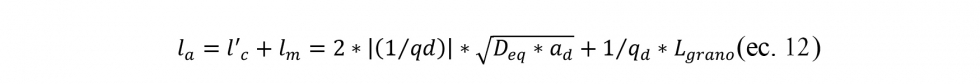
Por otro lado, también estipula la distancia periódica entre dos surcos adyacentes sobre la superficie de muela solidario a la trayectoria de diamantado:
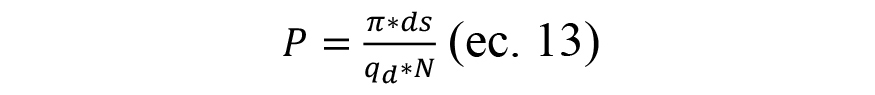
Donde N es el número de diamantes infiltrados sobre la periferia del diamantador.
Por último, la resta entre ambas distancias determinará el gap o la distancia en la que el diamantador no entrará en contacto con la muela.
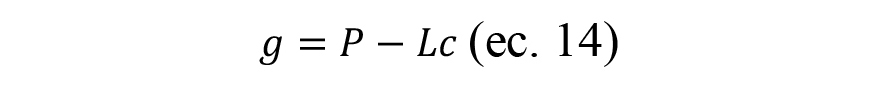
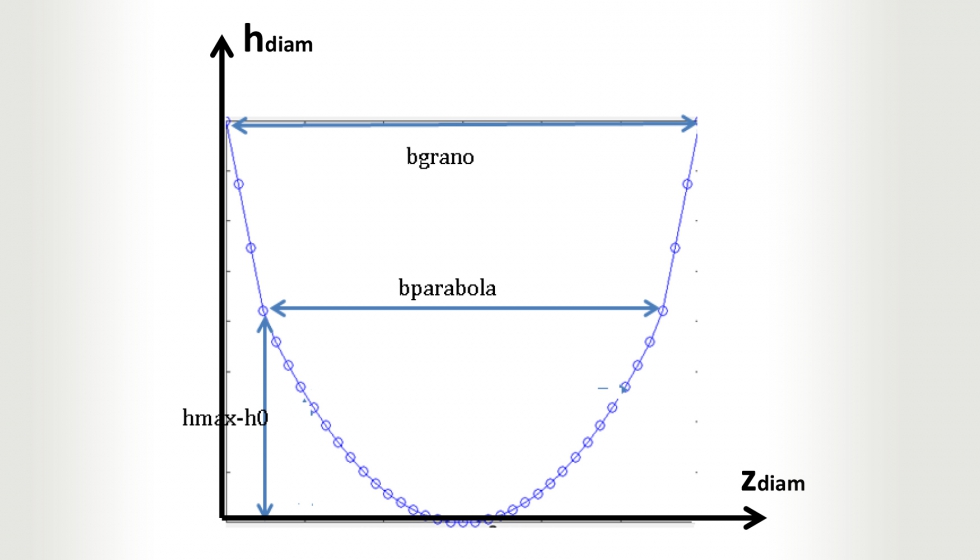
Como se muestra en la ilustración 11, es importante recalcar que el perfil de los surcos generados en la trayectoria del diamantado se aproxima a un perfil parabólico debido a que la profundidad de diamantado resulta mucho menor que el diámetro de la muela y el diámetro del disco (ad << ds). Considerando dicha simplificación, el surco generado en dirección del diamantado se puede expresar por el sistema de ecuaciones 13:
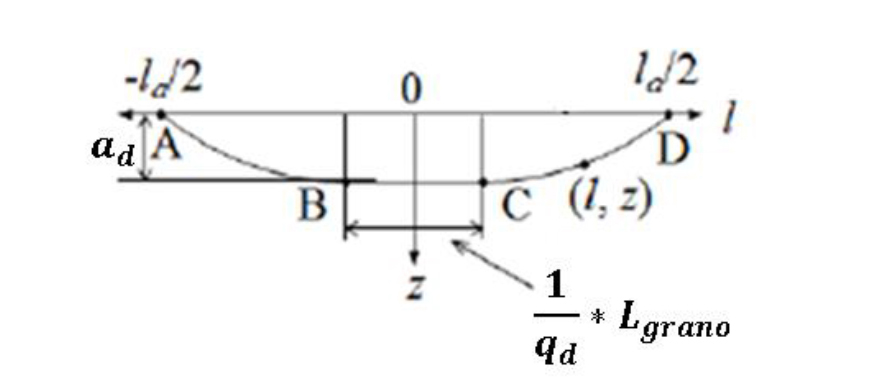
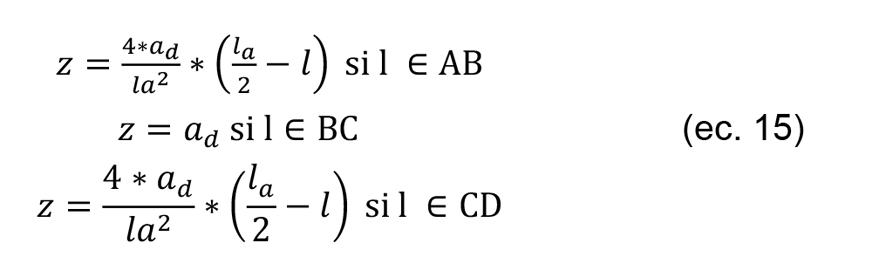
donde A=(-la/2,0), B=(-Lgrano/2qd, ad), C==(Lgrano/2qd, ad) y D=(la/2,0).
2.6. La cinemática del proceso de diamantado. Definición de trayectorias
La trayectoria del disco diamantador sobre la muela quedará totalmente definido en función de los parámetros de diamantado, la geometría del diamantador y las longitudes de corte del diamantado. En coordenadas cilíndricas las ecuaciones que definen la trayectoria del disco diamantador a lo largo del tiempo quedarán definidos por las ecuaciones 15 y 16:
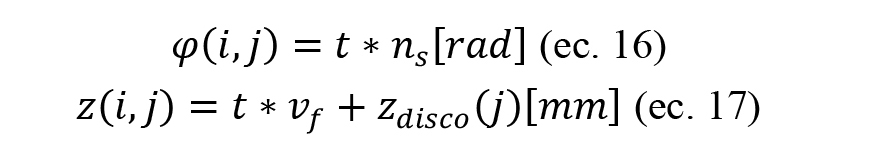
En caso de suponer una muela de diámetro ‘ds’ y exista contacto entre dicha muela y diamantador, el valor de la coordenada radial será:
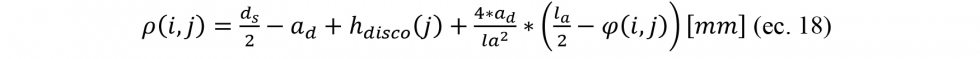
Mientras en caso de que no exista contacto la coordenada radial será igual al radio de la muela antes del diamantado:
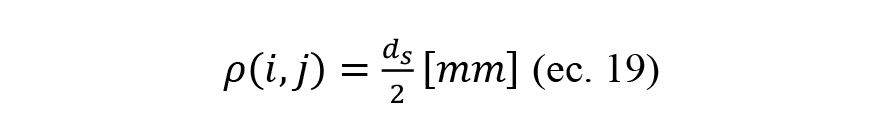
Donde zdisco y hdisco son las coordenadas del el perfil efectivo geométrico de la muela en dirección axial y en dirección radial de los diamantes de la moleta (ver ilustración 9).
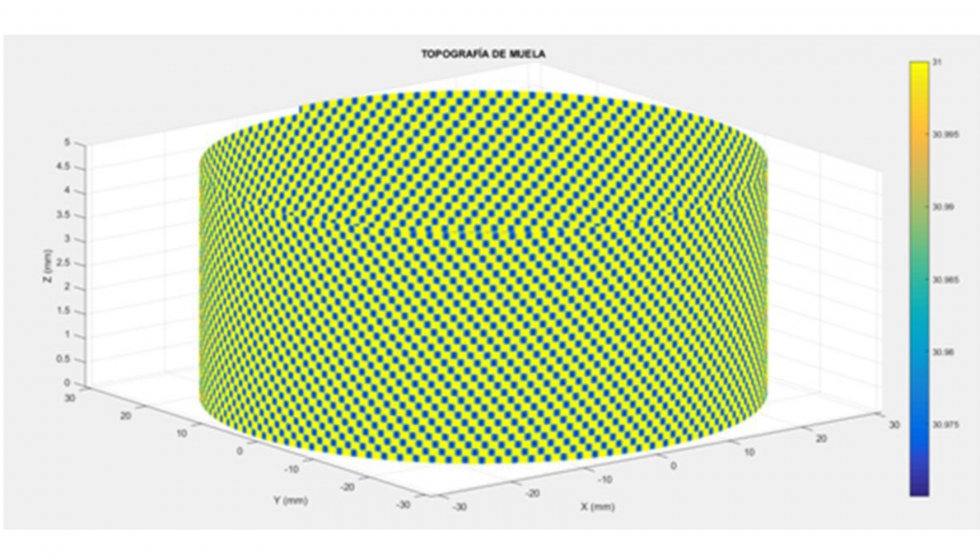
De esta manera, se obtiene la topografía de una muela diamantada con un disco de diamantes infiltrados, aún sin considerar la distribución de los granos sobre la periferia de la muela (ilustración 14).
2.7. Interacción entre muela y diamantador
Una vez obtenidas las matrices de que definen la topografía de la muela y la que define las trayectorias que deja el diamantado sobre la muela, se extraen los perfiles superficiales en dirección axial, comparándolas para quedarse con un perfil de mínimos en las cotas radiales, simulando así las fracturas de grano.
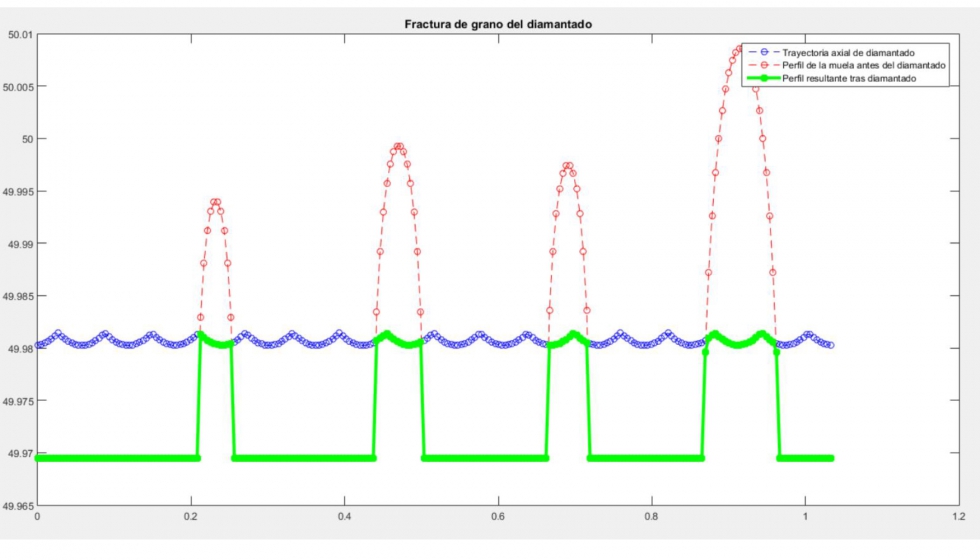
Ilustración 16: Interacción de las trayectorias de diamantado (azul) y el perfil de muela antes del diamantado (rojo). En verde se muestra el perfil de mínimos resultante,
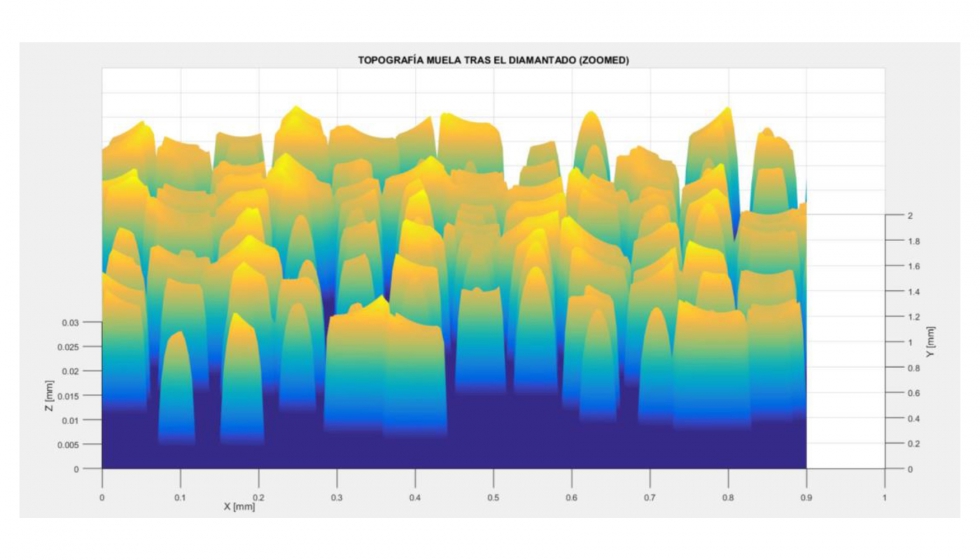
En la ilustración 17 se puede observar la topografía en una superficie de 0,9 x 2 mm resultante de la simulación del diamantado de una muela con tamaño de grano 150, que se ha obtenido solapando los perfiles resultantes uno tras otro.
2.8. Resultados del modelo cinemático
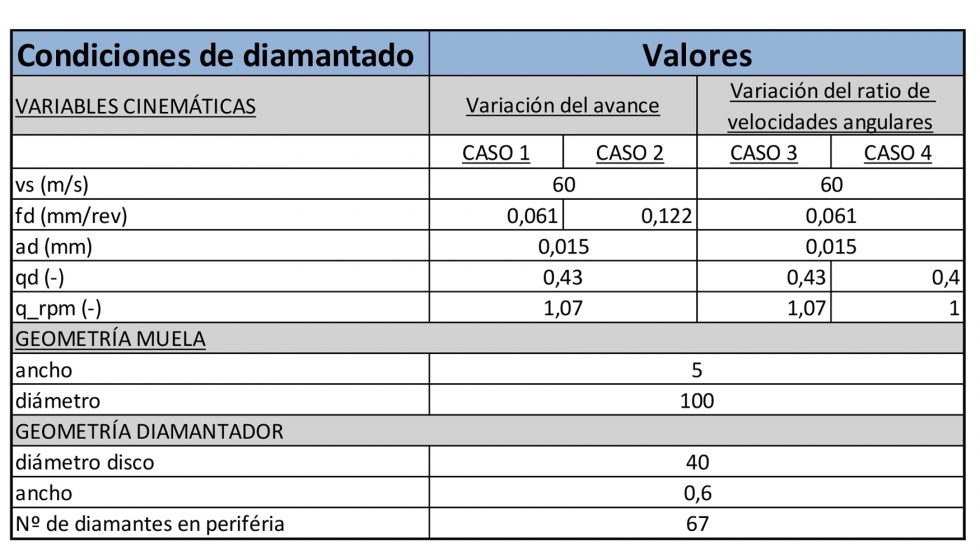
Una vez simulada la topografía tras el diamantado es posible evaluar el número de granos sobre la periferia de la muela o el número de filos sobre dicha periferia, ya que es posible que un grano abrasivo tenga más de un filo de corte que participará en el proceso de corte. A modo de ejemplo se ha lanzado la simulación de una muela A150K8V y se ha evaluado el número de los abrasivos sobre la superficie de la muela tras el diamantado a las condiciones de la tabla 3. En las primeras simulaciones se ha variado tanto el avance del diamantador (vf) como la ratio de velocidades lineales entre muela y diamantador (qd).
Destacar que las velocidades los diámetros de muela y de disco resultan reducidos comparándolos con los valores reales. Por ello, los valores de las velocidades de avance del disco han sido altas en estas primeras simulaciones. Sin embargo, estas comparaciones pueden resultar apropiados para observar las influencias de la velocidad de avance del diamantador y la relación de velocidades de manera preliminar.
En base a estas variables de entrada, se mostrará un primer análisis breve de las influencias de los parámetros cinemáticos del diamantado en la topografía de muela.
2.8.1 Influencia del avance del diamantado (vd)
En las ilustraciones 18 y 19 se muestran las topografías de muela resultantes de los casos 1 y 2.
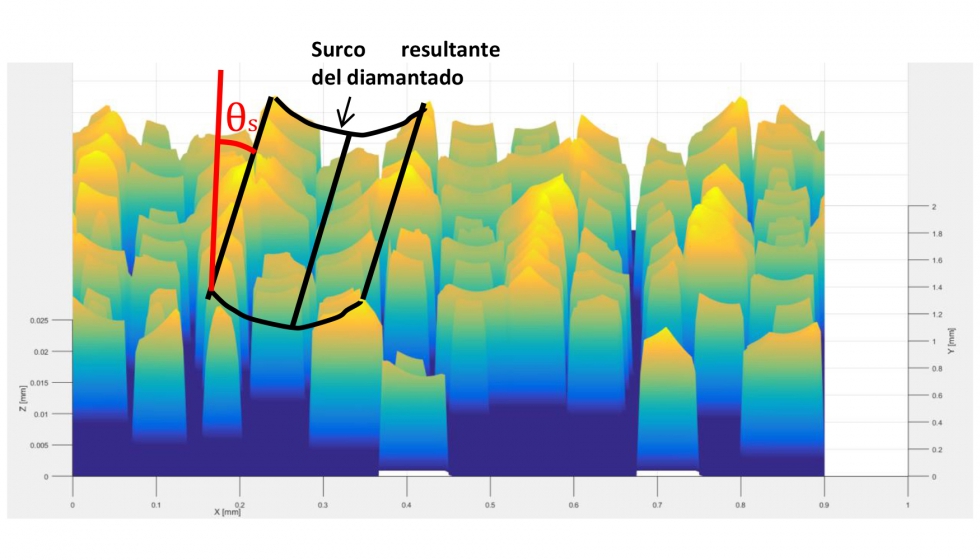
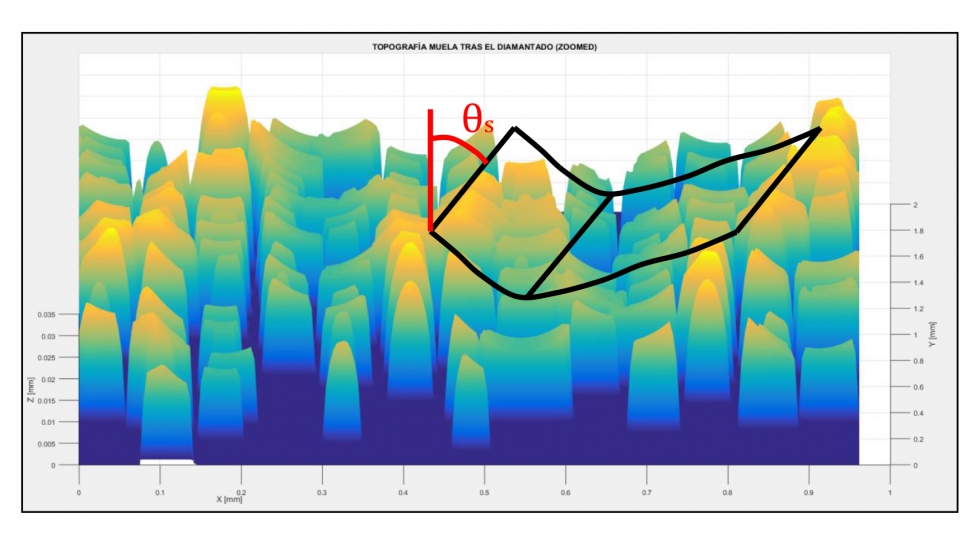
A primera vista, se observa un apreciable cambio entre el paso de los patrones helicoidales entre el caso 1 y 2. Además, el ángulo de los surcos respecto a la dirección axial (θs) también varía considerablemente. Si analizamos las topografías anteriores con mayor detenimiento, podemos observar que al aumentar el avance de diamantado aumenta el paso de la hélice generada en el diamantado.
Otro factor apreciable que podrá influir en el proceso de rectificado y en el copiado de los surcos sobre las superficies de las piezas finales, es el número de granos o número de filos activos en la superficie de la muela que deja el diamantado. Se aprecia que al aumentar el avance (caso 2) el número de picos (en color amarillo) ha bajado considerablemente en el área de evaluación.
El modelo permite obtener una tabla con los valores del número de abrasivos sobre la superficie de muela, el volumen de material arrancado por una pasada de diamantado, y los parámetros característicos de la hélice como el ángulo, el paso o la profundidad (ver tabla 5). Las tendencias mencionadas son verificadas por los resultados mostrados en la tabla 5.
2.8.2 Influencia de la relación de velocidades angulares entre muela y disco diamantador.
En los casos 3 y 4 cuyos parámetros de entrada se muestran en la tabla 4, se ha variado la relación de velocidades angulares (qrpm) entre muela y disco. Una relación de velocidades angulares entera, supone que mientras el disco diamantador da N vueltas, la muela lo hará k*N veces donde k es un número entero. Esto significa que serán siempre los mismos diamantes del disco los que entraran en contacto con el surco marcado en la vuelta anterior de la muela.
Así, al diamantar con una relación de velocidades angulares entero se genera un surco paralelo a la dirección axial de la muela. A su vez, el paso de diamantado se ve reducido y es igual a la velocidad de avance del diamantado (en mm/rev), ya que vuelta a vuelta se solapan las trayectorias de diamantado. En las ilustraciones 20 y 21 se observan las diferencias entre utilizar una relación no entera y entera (casos 3 y 4):
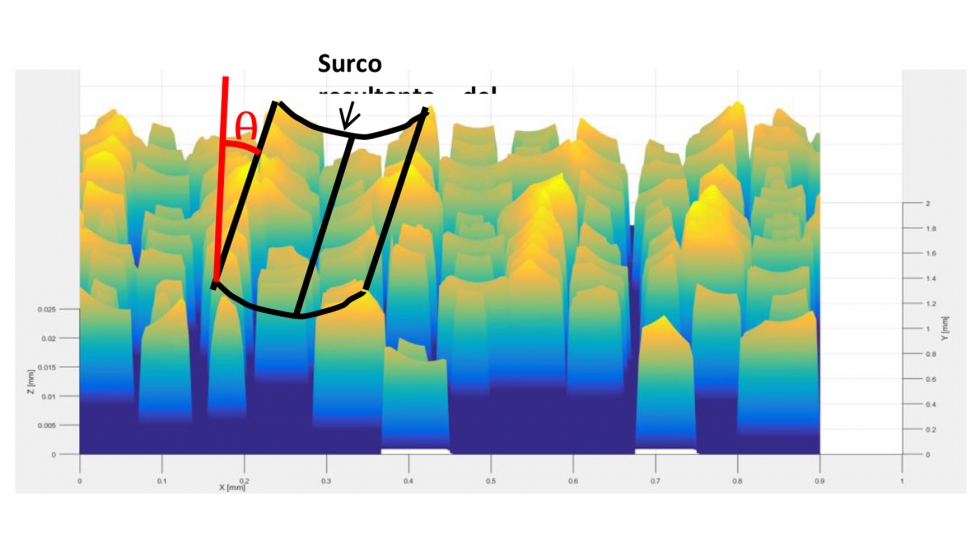
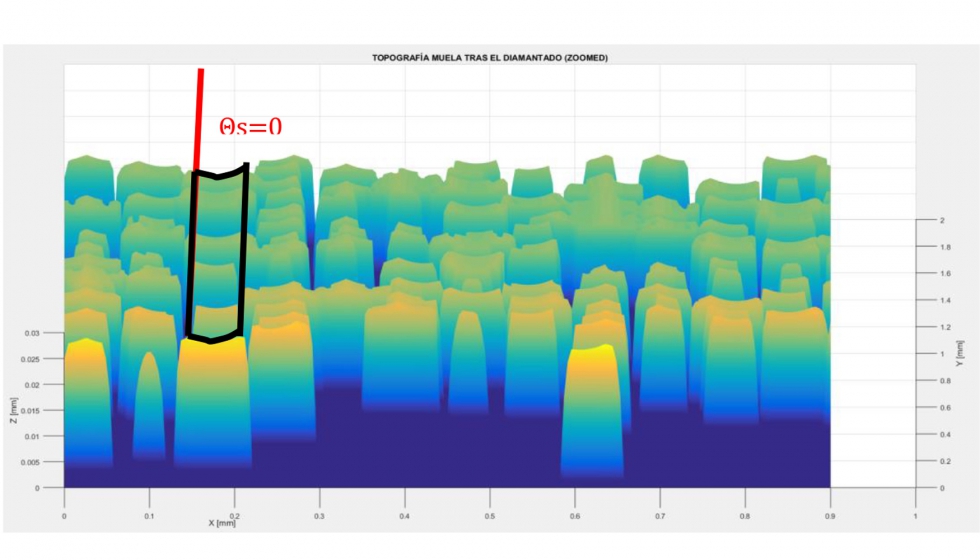
Analizando los perfiles de rugosidad obtenidos de las topografías resultantes (ilustraciones 22 y 23), también se confirman estas tendencias:
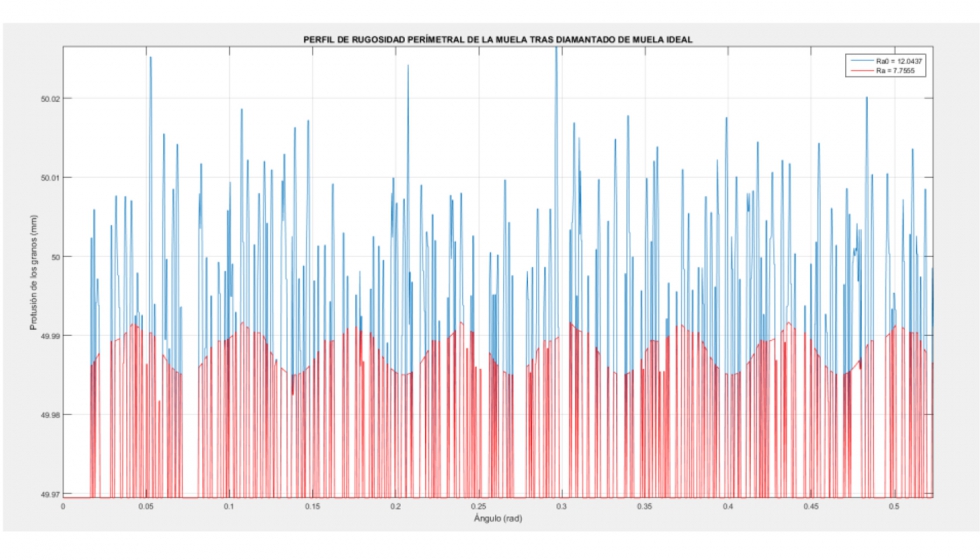
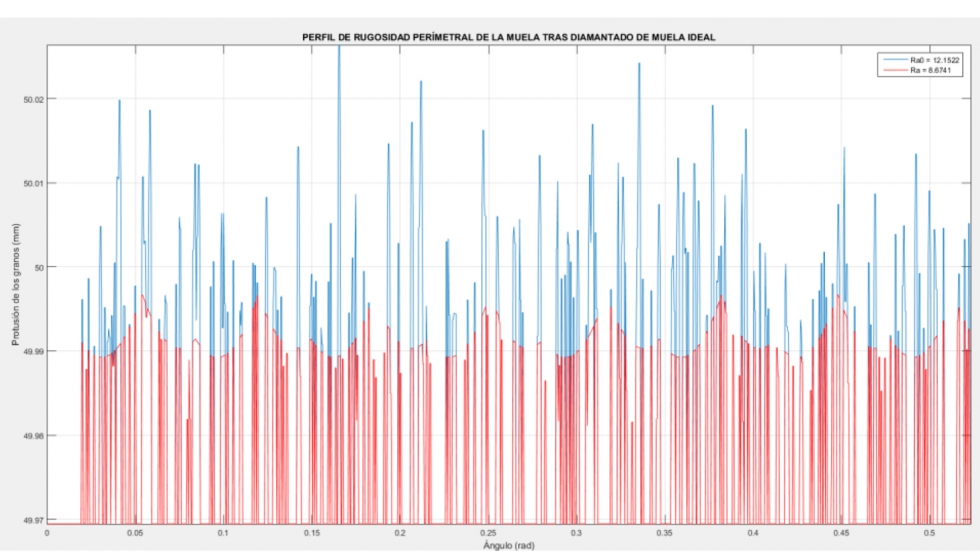
Lo más remarcable que se puede extraer de los perfiles resultantes, es que la distancia entre surco y surco depende de la velocidad del avance. También se puede destacar que la profundidad de los surcos resulta menor al diamantar con unas relaciones de velocidad angulares enteros (comparar ilustraciones 20 y 21).
Los resultados del modelo para cada uno de los casos se muestran en la tabla de a continuación:
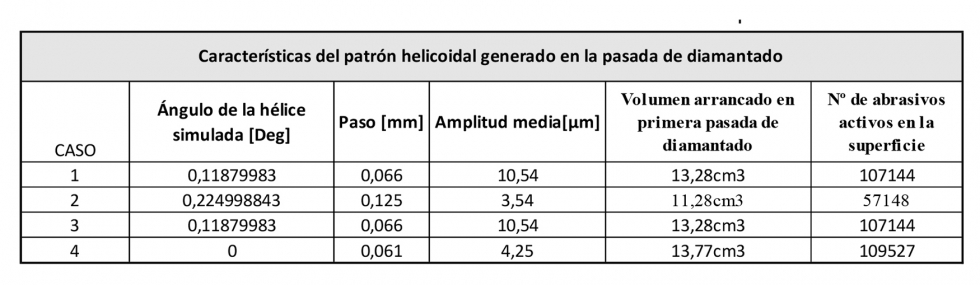
En estas primeras simulaciones se ha pretendido que el modelo se comporte de forma robusta frente a diferentes parámetros de diamantado. Sin embargo todavía queda el trabajo de validar el modelo y compararlo con mediciones de los ensayos que realizarán.
3. Conclusiones y trabajo futuro
5. Referencias
[Bas. 2008] Baseri, H., Rezaei, S. M., Rahimi, A., & Saadat, M. (2008). Analysis of the disc dressing effects on grinding performance—part 1: simulation of the disc dressed wheel surface. Machining Science and Technology, 12(2), 183-196.
[Bau, 2013] Baumann, M., Bauer, F., Haas, H. W., & Baitinger, G. (2013). How to measure lead in sealing technology? Sealing Technology, 2013(7), 8-12.
[Bri. 1995] Brinksmeier, E., & Cinar, M. (1995). Characterization of dressing processes by determination of the collision number of the abrasive grits. CIRP Annals-Manufacturing Technology, 44(1), 299-304.
[Cao 2013] Cao, Y., Guan, J., Li, B., Chen, X., Yang, J., & Gan, C. (2013). Modeling and simulation of grinding surface topography considering wheel vibration. The International Journal of Advanced Manufacturing Technology, 66(5-8), 937-945.
[Chen 1996] X. Chen, W.B. Rowe. Analysis and simulation of the grinding process. Part I: Generation of the grinding wheel surface. International journal Of Machine Tool and Manufacturing, v. 36 (1996), pp. 871-882
[Cho. 2013] Chowdhury, M. A. K., Akihiko, Kubo, Tamaki, J. I., & ULLAH, A. S. (2013). Computer-aided simulation of rotary diamond dressing based on kinematic analysis. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 7(4), 506-520.
[Dar. 2013] Darafon, A., Warkentin, A., & Bauer, R. Simulation of single point dressing in grinding.
[Hou 2003] Hou, Z. B., & Komanduri, R. (2003). On the mechanics of the grinding process–Part I. Stochastic nature of the grinding process. International journal of machine tools and manufacture, 43(15), 1579-1593.
[Kos. 1997] Koshy, P., Jain, V. K., & Lal, G. K. (1997). Stochastic simulation approach to modelling diamond wheel topography. International Journal of Machine Tools and Manufacture, 37(6), 751-761.
[Kun, 2016] Kundrák, J., Gyáni, K., Markopoulos, A. P., Felho, C., & Deszpoth, I. (2016). theoretical analysis of twist parameters in advanced grinding processes. Academic journal of manufacturing engineering, 14(4).
[Mal. 2008] S. Malkin, C.S. Guo. Grinding Technology, Theory and Applications of Machining with Abrasives (2nd ed.), Effis Horwood Limited (2008).
[Mar. 2004] Marinescu, I. D., Rowe, W. B., Dimitrov, B., & Inaski, I. (2004). Tribology of abrasive machining processes. Elsevier.
[MBN, 2008] “Mercedes-Benz-Werksnorm MBN 31 007-07” Copyright Daimler 2008 (14 pages).
[Nag, 2016] Nagy, N., & Kundrak, J. (2016). Influences of the technological parameters on the surface twist in grinding.
[Nor, 2014] www.noritake.co.jp/eng/products/abrasive/support/support_grinding/dressing.html
[Pah. 1954] G. Pahlitzsch, J.B. Appun. Effect of Truing Conditions on Circular Grinding, Industrial Diamond Review, v. 14 (1954), 185-189, 212-217.
[San. 2011] Sanchez, L. E. A., Jun, N. X., & Fiocchi, A. A. (2011). Surface finishing of flat pieces when submitted to lapping kinematics on abrasive disc dressed under several overlap factors. Precision Engineering, 35(2), 355-363.
[See, 2009] Seewig, J., & Hercke, T. (2009). Lead characterisation by an objective evaluation method. Wear, 266(5), 530-533.
[Set. 2017] Setti, D., Ghosh, S., & Rao, P. V. (2017). A method for prediction of active grits count in surface grinding. Wear, 382, 71-77.
[Shu. 2013] Schubert, A., Zhang, R., & Steinert, P. (2013). Manufacturing of Twist-Free Surfaces by Hard Turning. Procedia CIRP, 7, 294-298.
[Vog 2014] Vogt, R., & Bock, E. (2014). Shaft Surface Effects on Radial Shaft Seals. In Encyclopedia of Lubricants and Lubrication (pp. 1739-1746). Springer Berlin Heidelberg.









































































