Ik4-Tekniker participa en el proyecto europeo DynXperts
Proyecto DynXperts, cabezales de gran potencia y elevada velocidad de giro para una mejor productividad
Goialde High Speed e Ik4-Tekniker llevan años investigando la aplicabilidad de los cojinetes magnéticos activos a los cabezales de alta velocidad y han desarrollado varios prototipos en esta línea. En el marco del proyecto europeo DynXperts, Ik4-Tekniker ha trabajado en la resolución de la inestabilidad, aportando amortiguamiento al primer modo de vibración del eje mediante el control de los cojinetes magnéticos. Así, se ha conseguido multiplicar por seis la capacidad productiva del cabezal, evitando las inestabilidades de mecanizado.
1. Introducción
Las máquina-herramientas empleadas para el mecanizado de piezas de aluminio necesitan emplear cabezales de una gran potencia y una elevada velocidad de giro para obtener grandes productividades. Para estas aplicaciones de alta velocidad se utilizan habitualmente cabezales con rodamientos cerámicos. Los rodamientos, en general, tienen una vida útil y cada cierto tiempo de uso, que depende se sus condiciones de trabajo, es necesario reponerlos por su desgaste.
La tecnología de cojinetes magnéticos activos, que permite sustentar los ejes sin contacto mecánico y por tanto sin desgaste de los cojinetes, permite en sus aplicaciones un funcionamiento con mucha menor necesidad de mantenimiento.
Los cabezales con cojinetes magnéticos, sin embargo, son susceptibles de problemas de inestabilidad (llamados Chatter) en el mecanizado, debido principalmente a la falta de amortiguamiento. En un cabezal con rodamientos, son estos los que proporcionan la rigidez y el amortiguamiento. En el caso de cabezales con cojinetes magnéticos la rigidez y el amortiguamiento se deben conseguir mediante el control de las fuerzas en los cojinetes magnéticos.
A falta de amortiguamiento, durante los procesos de mecanizado se dan condiciones de inestabilidad relacionados con los modos de vibración del eje del cabezal. Estas inestabilidades provocan niveles de vibración muy elevados, que pueden obligar a realizar una parada de la máquina. A mayor profundidad de corte, mayor es el riesgo de inestabilidad, y así, en cabezales con poco amortiguamiento de los modos de vibración, este factor puede limitar muy fuertemente la productividad de la máquina.
En este artículo presentamos el cabezal desarrollado por Goialde High Speed e Ik4-Tekniker y los resultados obtenidos durante el proyecto DynXperts. Durante este proyecto donde Ik4-Tekniker y Goialde High Speed han colaborado con otras 11 empresas, centros tecnológicos y universidades (entre ellas Ik4-Ideko, líder del proyecto, Soraluce y la Universidad del País Vasco (UPV/EHU), se ha conseguido aumentar 7 veces la productividad del cabezal magnético.
El cabezal magnético
El cabezal magnético utilizado durante el proyecto DynXperts (Ilustración 1) es un cabezal de 70 kW de potencia nominal y 36.000 rpm-s de velocidad máxima.

El cabezal lleva dos cojinetes magnéticos radiales, uno en la parte frontal y otro en la parte trasera. Cada uno de estos cojinetes está formado por cuatro electroimanes y dos sensores de posición sin contacto (Ilustración 2, izquierda), que mediante fuerzas atractivas ejercidas sobre el rotor, permiten controlar la posición de este en un plano. Mediante dos cojinetes radiales y un cojinete axial, se consigue controlar el posicionamiento del eje en levitación, en cinco grados de libertad (el sexto g.d.l siendo el giro del eje).
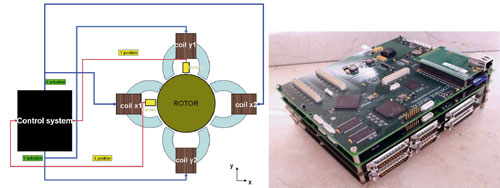
Ilustración 2: Al lado izquierdo, imagen conceptual de un cojinete magnético radial, con sus cuatro bobinas, sus dos sensores y el sistema de control. En el lado derecho, fotografía de la electrónica de control desarrollada en Ik4-Tekniker para control de sistema en levitación magnética.
El control se ejecuta en una electrónica desarrollada en Ik4-Tekniker (Ilustración 2, derecha), que consta de tres partes principales: una FPGA que realiza el control del HW y realiza también las operaciones de filtrado de mayor frecuencia de muestreo; un DSP que realiza el control en tiempo real del posicionamiento del eje en 5 gdls; y un procesador dedicado a la monitorización y a comunicación con elementos externos.
2. Análisis dinámico
2.1 Análisis dinámico teórico y experimental del cabezal
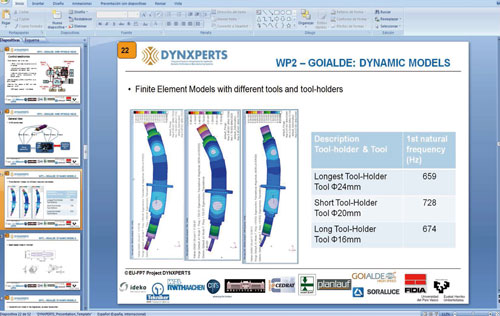
El análisis dinámico del eje del cabezal, realizado por elementos finitos, muestra un primer modo de vibración alrededor de 660 Hz (Ilustración 3).
Durante el proyecto DynXperts se ha desarrollado la posibilidad de realizar análisis dinámicos utilizando los propios cojinetes magnéticos. Para ello, se introduce una perturbación en forma de modulación lineal de frecuencia en la intensidad de uno de los cojinetes, y se miden los desplazamientos provocados por esa perturbación. Después, se calcula la función de transferencia entre la intensidad de las bobinas y la posición medida (Ilustración 4, izquierda). Se observa que el primer modo de vibración se encuentra en 590 Hz, y tiene un factor de amortiguamiento (amortiguamiento estructural del eje) de un 0,5 %.
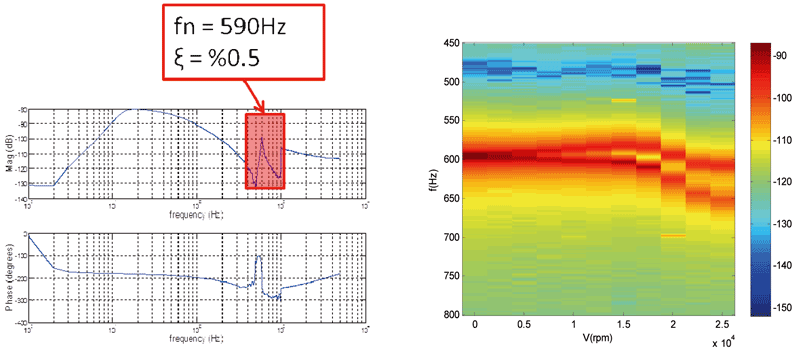
En los sistemas giratorios, las frecuencias naturales evolucionan con la velocidad de giro. Este efecto suele ser más pronunciado en sistemas de alta inercia, pero también se hace sentir en sistemas de muy alta velocidad de giro como el que estamos tratando. Sacando la función de transferencia a distintas velocidades de giro, entre 0 rpm y 25000 rpm, conseguimos observar la evolución del primer modo de vibración (Ilustración 4, derecha).
2.2 Análisis experimental del chatter
Como ya hemos indicado en la introducción, son los modos de vibración de la máquina que tienen poco amortiguamiento, los que provocan inestabilidades (chatter) durante el proceso de mecanizado. El análisis dinámico realizado en la sección anterior, nos muestra por lo tanto una posible causa potencial provocadora de chatter, ya que tenemos un modo de vibración entorno a 600 Hz, con un amortiguamiento muy bajo.
La Ilustración 5, muestra el espectro frecuencial de las posiciones medidas en los propios sensores del cabezal durante un proceso de mecanizado en el que se produce el fenómeno de chatter. Se observa que existe un nivel de vibración muy alto, en una frecuencia cercana al primer modo de vibración (indicado en rojo), además de distintos picos a frecuencias, donde es la frecuencia del chatter, es la frecuencia de giro del eje y es un número entero. Esto se corresponde con el patrón de chatter correspondiente al primer modo de vibración del eje.
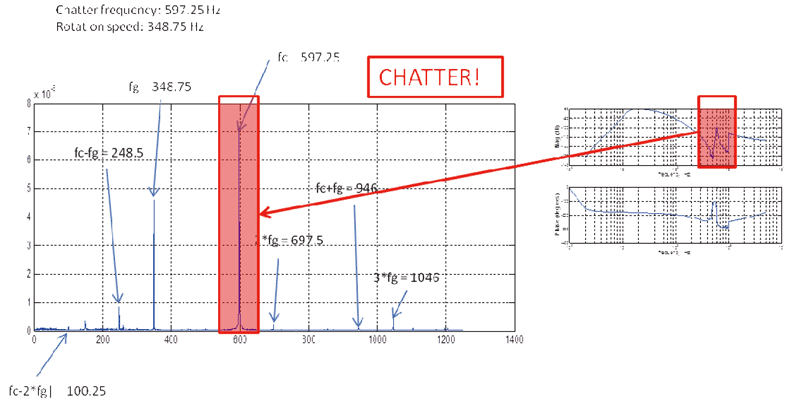
Deducimos, por lo tanto, de este ensayo, que la inestabilidad en el mecanizado que se está observando, está relacionada con la primera frecuencia natural del eje.
2.3 Análisis teórico del proceso de mecanizado
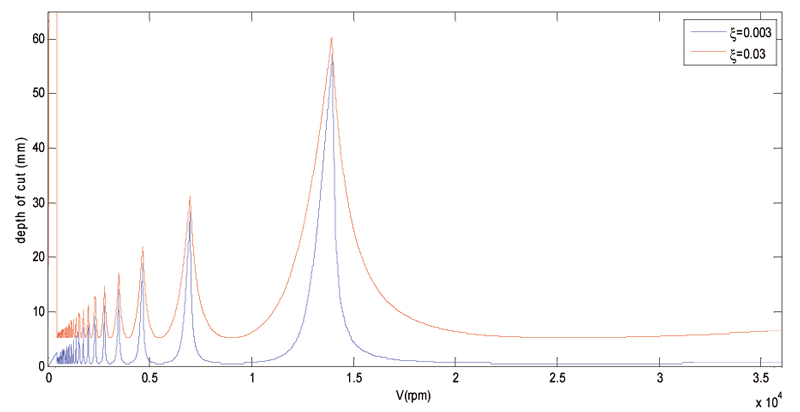
Los diagramas de estabilidad muestran la profundidad de corte máxima que se puede conseguir sin inestabilidad, a distintas velocidades de giro. En la Ilustración 6 se muestran los límites de estabilidad para un sistema con un único modo de vibración, con dos distintos valores del factor de amortiguamiento (línea azul, , línea roja, ). Se observa que un aumento del factor de amortiguamiento del modo del sistema se traduce en una mayor profundidad de corte alcanzable sin inestabilidades.
3. Amortiguamiento del primer modo de vibración
De todo lo anterior se deduce que debemos intentar amortiguar el primer modo de vibración del eje para conseguir mayores profundidades de corte (y por lo tanto mayor productividad) sin inestabilidades. Ese amortiguamiento de la frecuencia natural lo debemos conseguir, además, sin que afecte a la estabilidad del control de levitación. El control de levitación se realiza mediante un control en dos lazos: lazo de velocidad y lazo de posición. Una forma de conseguir amortiguar la frecuencia natural con este mismo control sería aumentar el ancho de banda del lazo de velocidad hasta la frecuencia que se quiere amortiguar. Sin embargo, el limitado ancho de banda de los actuadores magnéticos hace que el desfase a la frecuencia que se quiere amortiguar sea importante, y esto limita el ancho de banda del lazo de velocidad. No conseguimos por lo tanto llegar a amortiguar las frecuencias que nos interesan.
La pregunta que nos planteamos es, por lo tanto, la siguiente: ¿Cómo podemos amortiguar un modo de vibración que se encuentra al límite del ancho de banda de los actuadores? ¿Y cómo lo hacemos sin que ello afecte a la estabilidad del control de levitación? La respuesta aplicada en el proyecto DynXperts ha sido la siguiente: introduciendo amortiguamiento extra, sólo en las frecuencias relativas al modo de vibración. Es decir, en lugar de intentar amortiguar todo el sistema, nos planteamos amortiguar solamente las frecuencias correspondientes al modo de vibración. Para ello, se ha diseñado la estructura de control mostrada en la Ilustración 7. Es decir, a la consigna de fuerza generada por el control de levitación de dos lazos, le sumamos una componente solamente en las frecuencias alrededor del modo de vibración. Mediante un filtro pasa-banda, se consigue que el efecto de este algoritmo añadido se sitúe en las frecuencias del modo, y que de esta forma no afecte al control de levitación (que se encuentra en anchos de bandas más bajos).
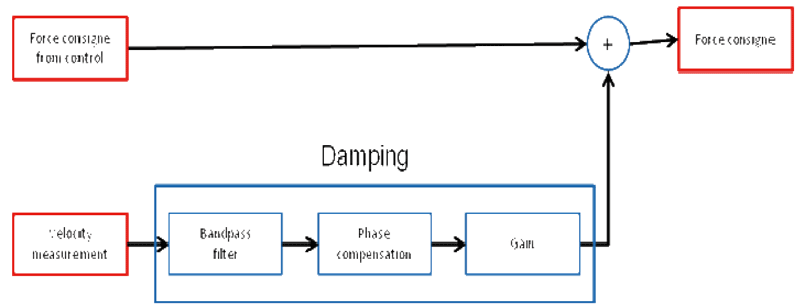
Ilustración 7: Esquema del algoritmo de amortiguación.
En cuanto al controlador que actúa sobre el modo de vibración, la idea es utilizar un Direct Velocity Feedback (DVF). Sin embargo, debido al limitado ancho de banda de los actuadores y el fuerte desfase que introducen en esas frecuencias (alrededor de 100º a 600Hz), el DVF no amortiguaría el sistema e incluso tendría el efecto contrario al deseado. Por eso se introduce en el algoritmo de control una compensación de fase, que compense el desfase de los actuadores en la banda de frecuencias del modo de vibración, haciendo que realmente se introduzca una amortiguación en dichas frecuencias.
3.1 Resultado de amortiguación
La Ilustración 8 muestra la respuesta ante perturbaciones con (rojo) y sin (azul) algoritmo de amortiguamiento. Se puede observar que se consigue amortiguar de manera muy notable el primer modo de vibración.
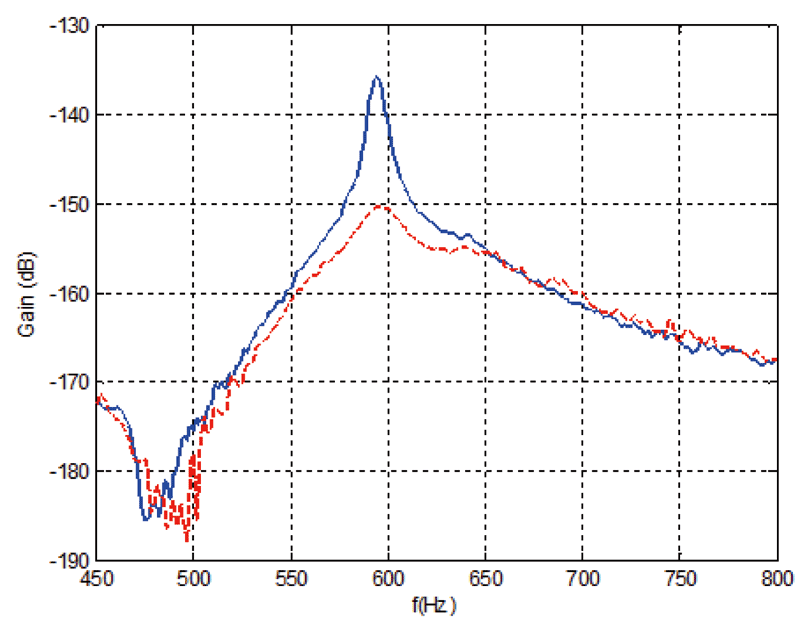
Con este nivel de amortiguamiento, y según el análisis teórico de la sección 2.3, se debe poder aumentar muchísimo la profundidad de corte, y por lo tanto la productividad del cabezal.
4. Resultados de mecanizado
4.1 Estabilización del proceso de mecanizado
En ensayos de mecanizado, se comprueba que la activación del algoritmo de amortiguación consigue estabilizar el proceso de mecanizado. Para ello, se ha iniciado un mecanizado sin algoritmo de amortiguación, y se ha activado el algoritmo en mitad del mecanizado. La Ilustración 9 (figura superior) muestra cómo la vibración se reduce de manera muy notable en el instante en el que se activa el algoritmo de amortiguación.
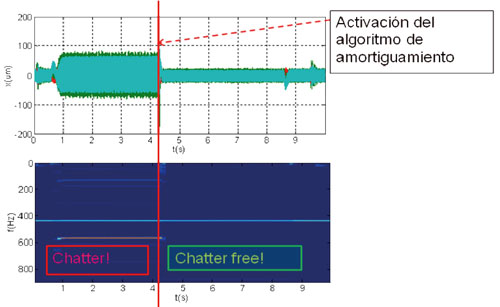
Ilustración 9: Activación del algoritmo de amortiguación durante el mecanizado. La figura superior muestra las medidas de vibración durante el mecanizado, y la inferior es una representación tiempo-frecuencia de una de esas señales. La herramienta contacta por primera vez con la pieza un poco antes de 1 s, y el mecanizado dura hasta 8,5 s. El algoritmo se activa un poco después de 4 s.
La figura de la parte inferior de la Ilustración 9, por otra parte, nos permite analizar evolución de las componentes frecuenciales de la vibración durante el ensayo. Se observa que hasta el instante de la activación del algoritmo existe una vibración cerca de la frecuencia natural del eje, y se puede observar el mismo patrón mostrado en la Ilustración 5.
En cuanto al resultado del mecanizado, la Ilustración 10 muestra el estado de la pieza tras el proceso de mecanizado (mecanizando de derecha a izquierda en la foto). Se observa claramente una transición en el momento de la activación del algoritmo, y las marcas desaparecen a la izquierda de la transición (es decir, cuando el algoritmo esta activado).

Este ensayo muestra, por lo tanto, que el algoritmo de amortiguamiento del primer modo de vibración consigue estabilizar el proceso de mecanizado.
4.2 Aumento de productividad
Al inicio del proyecto Dynxperts el chatter limitaba la productividad a unos 175 cm3/min de caudal de viruta. Al intentar llegar más allá de esos 175 cm3/min, las vibraciones por chatter se volvían tan grandes que obligaban a parar la máquina por riesgo a que el eje tocase los rodamientos de seguridad y se produjese una avería.
Con el algoritmo de amortiguación se consigue en estos momentos mecanizar a 1.125 cm3/min de caudal de viruta, es decir que se ha conseguido una productividad 6 veces mayor que la que se conseguía sin algoritmo de amortiguación. Además, la limitación en las nuevas condiciones no se debe al chatter. Es decir que el factor limitante en estos momentos no son las inestabilidades del proceso sino los impactos en entradas de herramienta que provocan desviaciones demasiado fuertes.
5. Conclusiones
En este articulo hemos mostrado el trabajo realizado dentro del proyecto europeo DynXperts, por una parte haciendo la caracterización dinámica del cabezal, y por otra parte implementando el algoritmo de amortiguación del primer modo de vibración. Con la técnica de amortiguación del primer modo de vibración se ha conseguido multiplicar por seis la capacidad productiva del cabezal, evitando las inestabilidades de mecanizado.
6. Agradecimientos
Los trabajos descritos en este artículo se han realizado dentro del Proyecto europeo DynXperts (Framework Program 7). Queremos agradecer la colaboración recibida, dentro del consorcio del proyecto, por parte de Ideko S. Coop, UPV/EHU y en particular por Goialde Hish Speed por cedernos un cabezal para realizar dichas pruebas.
















































