Introducción de los códigos abiertos PyNomo y Nomogen para la elaboración de nomogramas en el ámbito de la ingeniería civil y minera

La nomografía se puede definir como aquella rama de las matemáticas que se encarga de la representación gráfica de ecuaciones a través de nomogramas (también conocidos como ábacos) que permiten poner en relación tres o más variables resolviendo una de ellas cuando se conocen el resto. Esta área de las matemáticas fue implantada en 1880, y posteriormente desarrollada por Maurice d’Ocagne (Doerfler, 2009). El empleo de la nomografía tuvo su mayor desarrollo en el siglo pasado como una forma de resolver de forma rápida y precisa complejas expresiones matemáticas en sectores tan diversos como medicina, aeronáutica, hidráulica, química, física, matemáticas, electrónica, radio, balística, alimentación, etc. (Evesham, 1982; Adams, 1950). Por ello, son innumerables los ejemplos que han llegado hasta nuestros días y que aún aparecen en libros especializados de ingeniería, especialmente hidráulica, ingeniería civil, minería, etc. (SME, 2002). Además, en la actualidad, todavía es común que un gran volumen de documentación técnica, folletos de especificaciones técnicas y catálogos de equipos faciliten el cálculo de numerosas expresiones a través de nomogramas.

Tradicionalmente, la fase más laboriosa en la elaboración de cualquier nomograma ha sido dibujar apropiadamente las escalas y sus divisiones apropiadas para que ofrezcan el valor de la variable con una precisión adecuada, y esto ha sido uno de los factores que sin duda ha hecho que el estudio de los nomogramas y su aplicación haya quedado casi relegado al olvido en favor del uso de calculadoras programables u ordenadores personales. Sin embargo, los nomogramas todavía presentan ciertas potencialidades como son la de ayudar a entender la relación que existe entre las diferentes variables que forman una expresión matemática, no siempre tan evidente, por lo que la nomografía puede ser una herramienta fundamental en un contexto académico como son los estudios de ingeniería. Además, los nomogramas facilitan que personas sin conocimientos matemáticos o científicos previos puedan resolver complejas fórmulas con una adecuada precisión, algo muy útil cuando estas operaciones matemáticas son repetitivas.

En este sentido, en recientes años han aparecido dos códigos abiertos basados en la programación de Python, denominados PyNomo y Nomogen, creados por dos de los autores de este artículo (L.R. y T.B.), que permiten generar un nomograma en cuestión de segundos evitando los inconvenientes del pasado, incluso con nomogramas que presentan cierta complejidad de elaboración. El empleo de estos códigos, especialmente PyNomo, está ayudando a la generación de nuevos nomogramas, aunque aún de una manera muy testimonial y que no dejan de ser una curiosidad. Por ello, en este artículo se presentan las potencialidades de los programas PyNomo y Nomogen para generar nomogramas a través de varios ejemplos aplicados a la hidráulica.

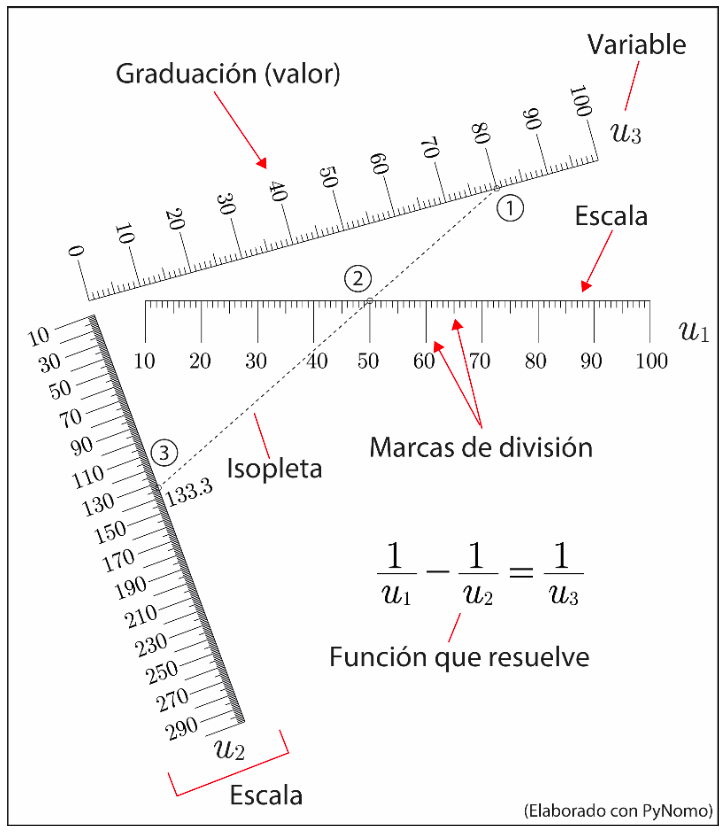
Un nomograma, por lo tanto, es una representación gráfica, generalmente bidimensional, que estará formado por una serie de ejes graduados, rectos o curvos, y tantos como variables tenga la ecuación, y en donde el valor de las variables será obtenido al unir estos ejes por una línea recta, denominada isopleta. En la figura 1 se facilita un ejemplo de nomograma, realizado con PyNomo en donde se han señalado los principales elementos que lo componen. Este nomograma resuelve la siguiente expresión:

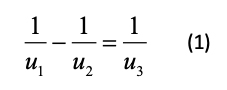
En el ejemplo de la figura 1 se observa que dibujando una línea recta (isopleta) que pasa por los dos valores conocidos de u₁ = 50 y u₃ = 80, y prolongándola hasta cortar la tercera escala, entonces nos proporcionaría el valor buscado de la tercera variable, siendo u₂ = 133.3, que resuelve la ecuación 1.

En esta sección se hace una breve introducción de los principales códigos actualmente existentes, PyNomo y Nomogen, para la generación de nomogramas. Para acceder a ellos, en los siguientes enlaces se facilita toda la documentación e indicaciones necesarias para su descarga, instalación y correcto manejo:

http://lefakkomies.github.io/pynomo-doc/introduction/introduction.html

https://github.com/lefakkomies/pynomo

Nomogen es muy útil para generar nomogramas que resuelven ecuaciones de hasta tres variables y PyNomo es mucho más completo al generar nomogramas que resuelven ecuaciones de hasta tres o más variables:

https://victoryepes.blogs.upv.es/2023/02/01/metodos-de-calculo-de-la-piedra-en-una-voladura-en-banco-de-una-cantera/

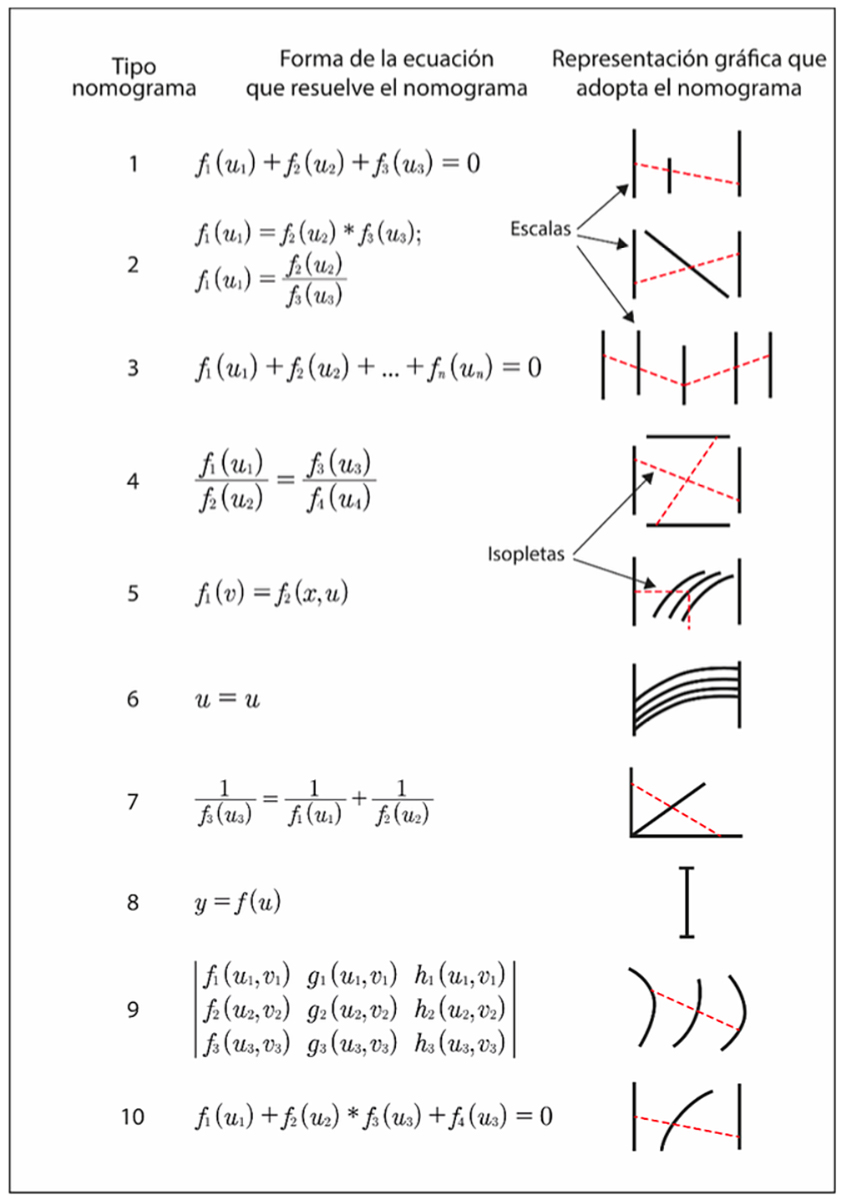
En este sentido, la figura 2 presentan los tipos de ecuaciones que pueden ser resueltas por nomogramas generados por PyNomo. En la columna de la derecha se facilita, de forma esquemática, el tipo de representación gráfica que adoptarían estos nomogramas.

El primero de ellos (Figura 3) se trata de un nomograma elaborado con PyNomo y compuesto de tres escalas paralelas y que ayuda a resolver la siguiente ecuación que proporciona el caudal de una pulpa mineral (sólidos + líquido) por cada t/h de sólidos que es necesario bombear (ETSIM-UPM, 1998):

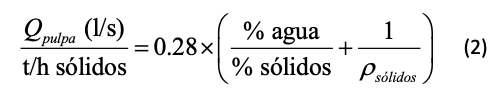
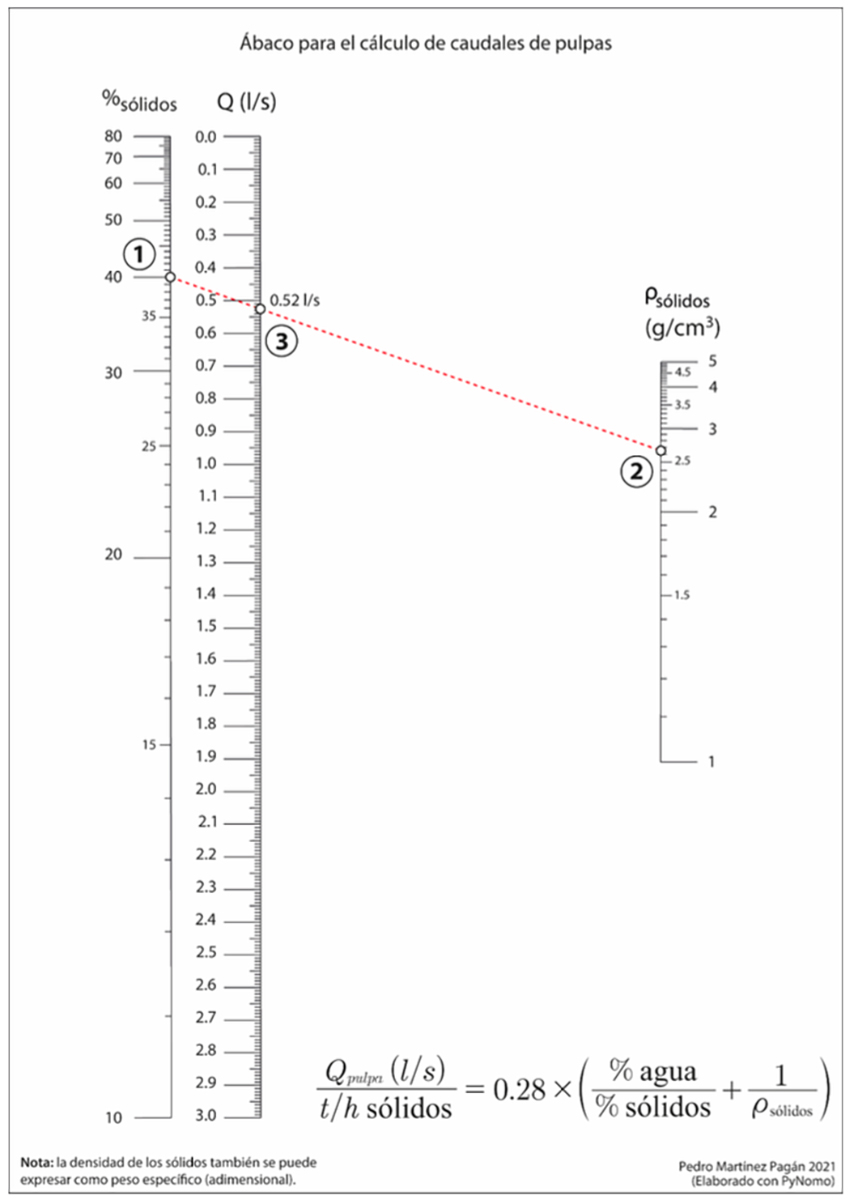
Así, para el ejemplo resuelto de la figura 3, se tiene que la recta dibujada, que une un valor estimado para la concentración de sólidos en peso del 40% y un peso específico para los sólidos de 2.7 g/cm³, daría un valor para el caudal total de pulpa (por tonelada por hora de sólidos a bombear) de 0.52 l/s.

A continuación, se presenta otro ejemplo de nomograma realizado esta vez con el código abierto Nomogen (Figura 4), en este caso el nomograma está compuesto por tres escalas graduadas curvas que proporcionan el valor del factor de fricción en tuberías en base a la ecuación de Colebrook y cuya expresión es (Bouso y Martínez Pagán, 2023):

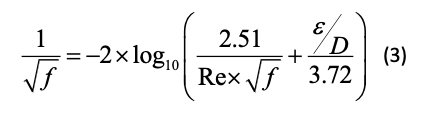
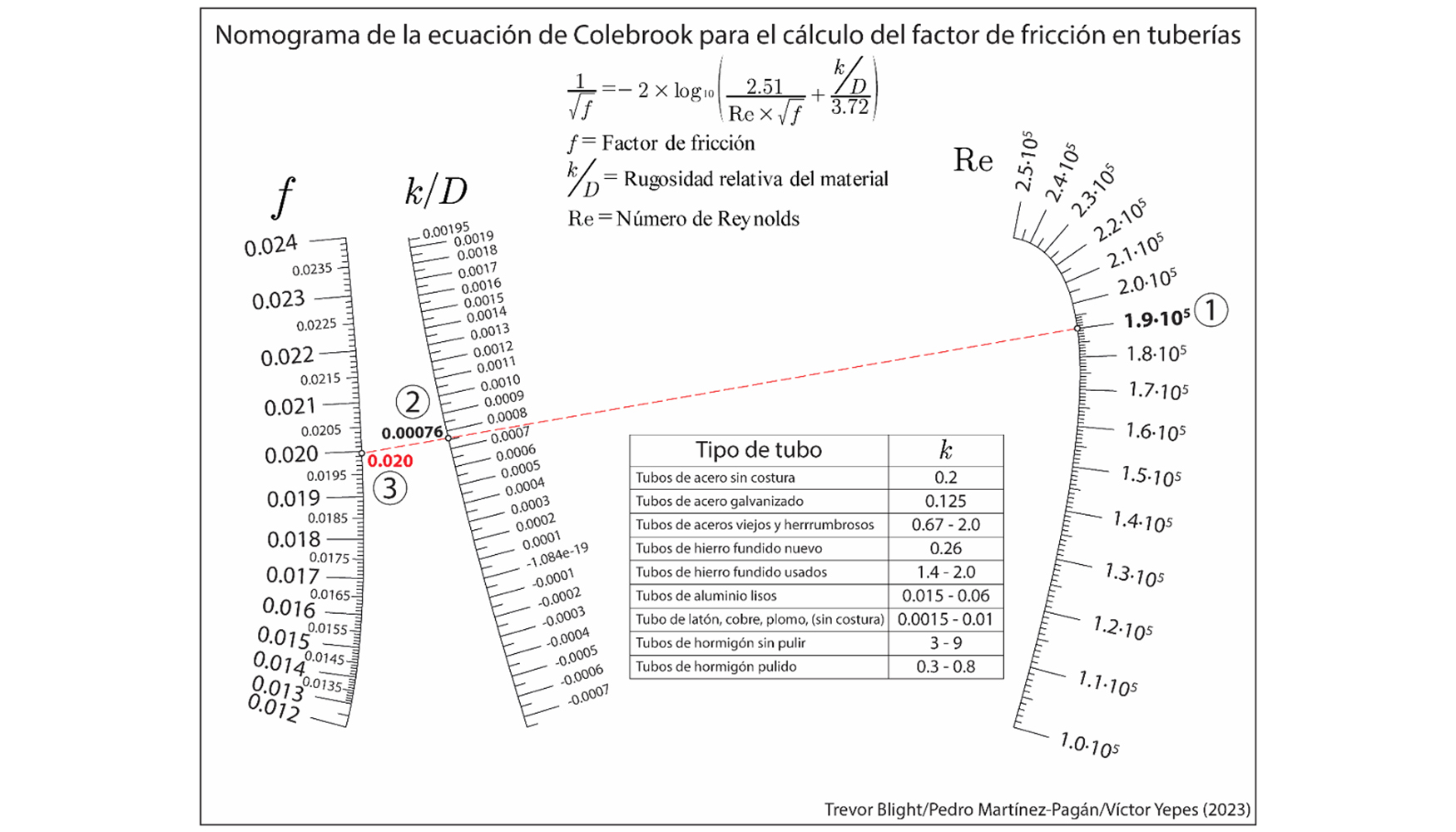
El ejemplo resuelto que ilustra la figura 4 muestra que trazando una línea recta que pase por un valor de 1.9x10⁵ para el número de Reynolds y por el valor de 0.00076 para la rugosidad relativa, proporcionaría un factor de fricción de 0.020. Lo interesante de este nomograma es que resuelve la dificultad de obtener de forma inmediata el factor de fricción por medio de la ecuación 3 al encontrarse éste en los dos miembros de la ecuación 3.

Otro ejemplo obtenido con Nomogen es el nomograma de la figura 5 que representa una ecuación útil para determinar el diámetro de descarga del hundido de un hidrociclón y que representa a la fracción gruesa que se obtiene con estos equipos de separación en procesos mineralúrgicos. Para este ejemplo se ha estimado una densidad de las partículas sólidas de 2.65 t/m³. Con esta densidad, la ecuación que se obtiene es la facilitada en la figura 5 donde para un valor de concentración de sólidos en peso (C_g) del 55% y un caudal de descarga (T_u) de 500 t/h se requeriría un diámetro de boquilla de 168.2 mm (d_u).

El siguiente ejemplo aborda un nomograma realizado con PyNomo para el cálculo de canales empleando la ecuación de Manning-Strickler (Figura 6). El caso propuesto establece que, para un caudal, Q, de 1 m³/s, una sección de canal, S, de 0.71 m², una velocidad del flujo, V, de 1.41 m/s, un coeficiente de rugosidad, K_s, de 65 m^1/3/s, y una sección, S, de 0.002 m², proporciona un radio hidráulico, R_h, de 0.33 m (Figura 6).

Finalmente, el último ejemplo es un nomograma elaborado con PyNomo que consiste en una ruleta de conversión de unidades de presión comúnmente empleadas en hidráulica y que de forma rápida permite conocer el valor equivalente entre mm de Hg, PSI (del inglés, pound per square inch), m.c.a. (metros de columna de agua), kN/m², etc. Lo interesante de los nomogramas creados con PyNomo (también con Nomogen) es que son producidos en formato vectorial (.pdf o .eps) con lo que son escalables a cualquier tamaño sin perder resolución, permitiendo por ello obtenerlos en grandes formatos para visualizar mejor las divisiones de sus escalas y trabajar cómodamente con ellos (Figura 7).

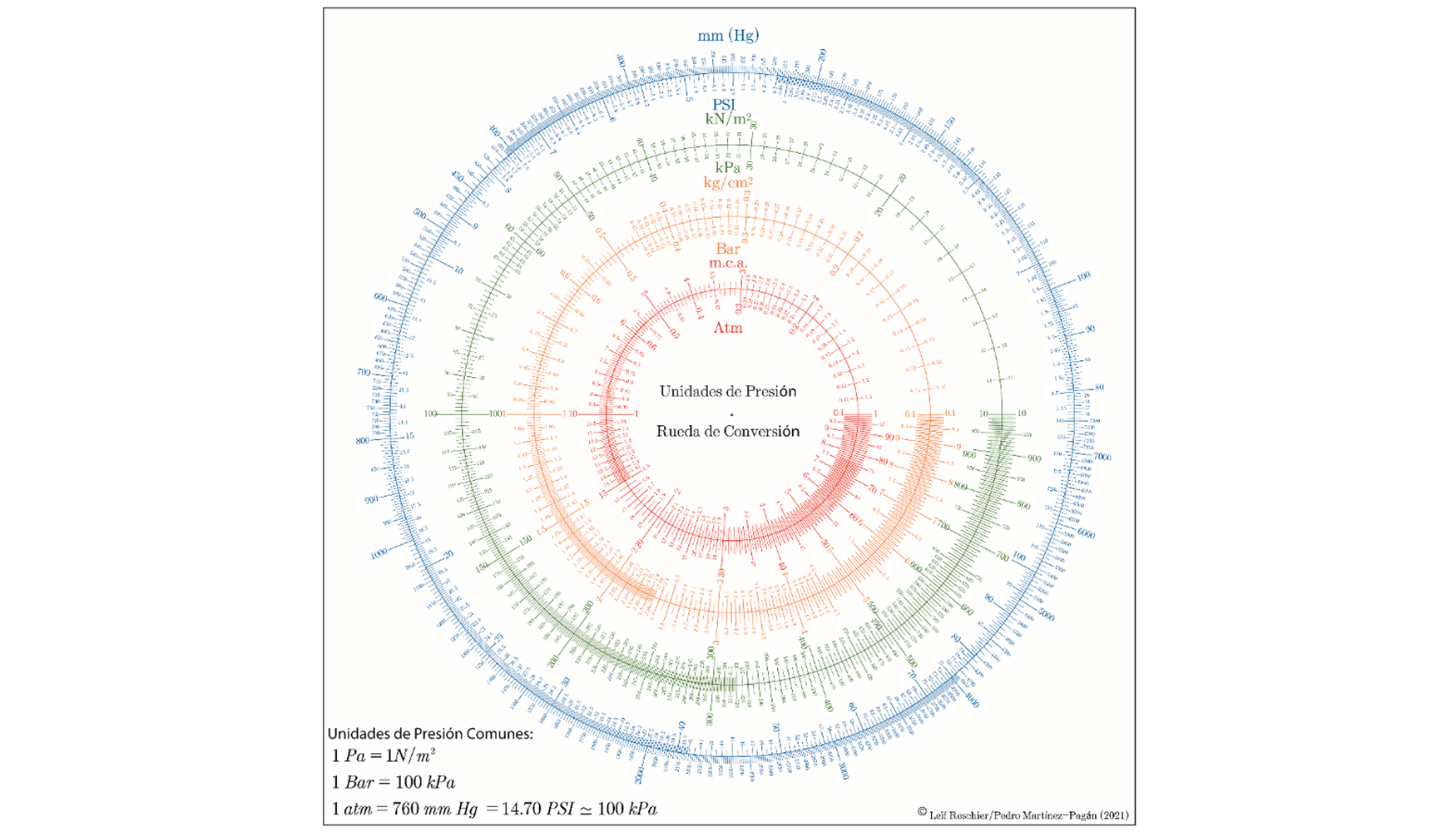
Figura 7. Rueda de conversión de unidades de presión.

En este trabajo se presentan dos códigos abiertos basados en código Python para la generación de nomogramas evitando los inconvenientes del pasado cuando su construcción era totalmente manual. Estos códigos permiten la generación rápida de nomogramas que permiten resolver un amplio abanico de ecuaciones con una adecuada precisión. Por ello, pueden ser muy útiles para generar nomogramas específicos al campo de la ingeniería en el que se necesiten.

Referencias

• Adams, D.P. (1950). An Index of Nomograms. The Technology Press of Massachusetts Institute of Technology, 174 pp.
• Bouso, J.L. and P. Martínez Pagán (2023). Bombeo de pulpas minerales. Diferentes procedimientos de cálculo. Rocas y Minerales, Fueyo Editores, no. 605 (Enero), 56-73.
• Doerfler, R. (2009). The Art of Nomography. The UMAP journal, 30 (4), 457- 494.
• ETSIM-UPM. (1998). Manual de áridos. Prospección, explotación y aplicaciones. 3ª Edición. Entorno Gráfico, S.L., Madrid, 607 pp.
• Evesham, H.A. (1982). The history and development of nomography. Docent Press, Boston, Massachusetts, p. 267 pp.
• Martínez-Pagán, P., Yepes, V. and M.A. Martínez-Segura (2023). Ejercicios resueltos de sistemas de transporte continuo: bombas y cintas transportadoras, 282 pp. https://upct.odilotk.es/opac/#fichaResultados.
• Martínez-Pagán, P., and L. Roschier (2022). Nomography: A Renewed Pedagogical Tool to Sciences and Engineering High-Education Studies. Heliyon, 12 pp. https://doi.org/10.1016/j.heliyon.2022.e09731.
• Mottola, G., and M. Cocconcelli (2023). Nomograms in the History and Education of Machine Mechanics. Foundation of Science, 31 pp. 10.1007/s10699-022-09890-w.
• Society for Mining, Metallurgy, and Exploration, SME (2002). SME Mining Reference Handbook. Raymond L. Lowrie, P.E. (Editor), 448 pp.
• Yepes, V. (2022). Gestión de costes y producción de maquinaria de construcción. Colección Manual de Referencia, serie Ingeniería Civil. Editorial Universitat Politècnica de València, 243 pp. Ref. 442.