Predicción de fragmentación ajustada y Burden en función de una granulometría requerida
Oscar Mundaca Muñoz. Líder Técnico. Enaex Mining Technical Solutions
19/09/2019En minería, uno de los parámetros más influyentes que apalanca los indicadores de rendimiento en la producción minera es la calidad de la fragmentación de la roca tronada, pues la granulometría puede limitar o aumentar los rendimientos de los equipos de extracción, como también los indicadores de los procesos de conminución en la planta. Por ende, determinar una configuración de Burden y Espaciamiento en función de una fragmentación que mejore el beneficio de minerales en procesos aguas abajo es clave para el negocio de las operaciones. En este artículo se desarrollará una metodología de ajuste a un Modelo de predicción de fragmentación de Kuz-Ram, junto con el desarrollo de formulismo de Burden con el grado de fragmentación deseada como una de sus variables.
La metodología y análisis de datos que se presentarán están en base a las pruebas de incorporación de un nuevo producto explosivo de Enaex en una operación minera de cobre del norte de Chile, fundamentando cómo es posible determinar una nueva configuración de diseño a partir de nuevos resultados granulométricos, tomando como variable una fragmentación requerida.

Metodología
La metodología utilizada para la ampliación de mallas en base al ajuste de predicción de fragmentación y desarrollo de un formulismo de Burden a partir de una granulometría requerida, se describe en los siguientes puntos:
- Analizar los parámetros de predicción de fragmentación.
- Analizar pruebas comparativas con un nuevo explosivo.
- Ajustar la curva granulométrica a un modelo de Rosin-Rammler.
- Comparar el modelo predictivo de fragmentación Kuz-Ram.
- Incorporar factores de ajustes y una metodología para su determinación.
- Desarrollar el formulismo de Burden en base a una fragmentación requerida.
- Establecer nuevos parámetros de diseño, en base a una predicción de fragmentación ajustada.
- Analizar los resultados y comprobar la adherencia a la curva estimada.
Parámetros de predicción de fragmentación
El modelo predictivo de fragmentación a analizar es Kuz-Ram, el cual fue desarrollado por Claude Cunningham (1983), quien se basó en el modelo de Kuznetsov sobre la estimación del tamaño medio de fragmentación y la función de distribución granulométrica de Rosin Rammler.
El tamaño medio de la roca (X50) se representa por medio de la siguiente función:
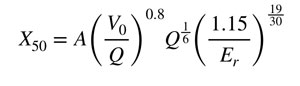
Donde:
- X50: Tamaño medio de la roca fragmentada (cm).
- A: Factor de roca.
- V0: Volumen de roca removida por una perforación (m3).
- Qt: Kilogramos de explosivos de TNT en el pozo.
- Q: Kilos de explosivo.
- Er: Potencia relativa al Anfo en peso.
Para determinar el factor de roca ‘A', es posible relacionarlo con el índice de volabilidad de Lilly ‘BI’ de la siguiente forma:
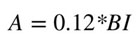
El índice de volabilidad ‘BI’ (Blastability index) se expresa a continuación:
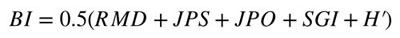
Donde:
- RMD: Parámetro que clasifica la descripción del macizo rocoso como quebradizo, fracturado o masivo
- JPS: Parámetro que representa ponderadamente el espaciamiento de los planos de diaclasas
- JPO: Parámetro que asigna un factor según la orientación de los planos de diaclasas
- SGI: Influencia de la gravedad específica. = 2.25*SG - 50
- SG: Densidad del macizo rocoso (Ton/m3)
- H’: Dureza = 0.05*RC
- RC: Resistencia a la compresión (MPa)
Los factores ponderados en relación a los parámetros de roca y estructuras del índice de volabilidad de Lilly, se expresan en la siguiente tabla:
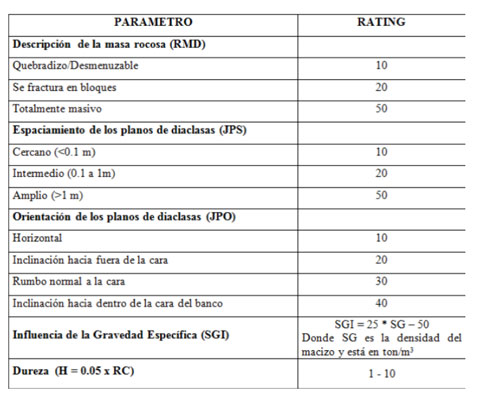
La ecuación de Rosin Rammler define la distribución de fragmentación mediante el siguiente modelo matemático:
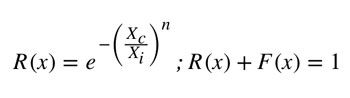
Desde el citado modelo, se puede obtener el tamaño de la roca correspondiente al % de material pasante requerido para analizar
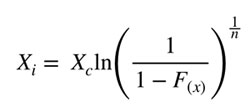
Donde:
- R(X): % de material retenido
- F(X): % de material pasante
- XC: Constante que representa el tamaño característico de la roca
- Xi: Tamaño de la partícula medida
- n: Índice de uniformidad de la distribución granulométrica
Calculando el tamaño medio para la curva de fragmentación se obtiene:
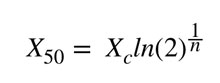
Igualando y reagrupando los términos para expresar la fragmentación en pulgadas, se puede despejar el tamaño característico de la roca de la siguiente forma:
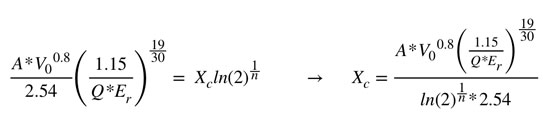
Cunningham también determinó el índice de uniformidad en relación a los parámetros de diseño y la desviación de perforación por medio de la siguiente ecuación:
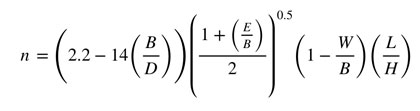
Donde:
- n: Índice de uniformidad en relación con los parámetros de diseño de perforación y voladura
- B: Burden (m)
- E: Espaciamiento (m)
- D: Diámetro de perforación (mm)
- W: Desviación estándar de la precisión de la perforación (m)
- L: Longitud de la carga explosiva (m)
- H: Altura de banco (m)
De esta forma obtenemos un modelo predictivo de distribución de roca fragmentada, por medio de los parámetros del tamaño característico de la roca ‘Xc’ y la uniformidad de la pila fragmentada’n’.

Pruebas comparativas con un nuevo explosivo
Para análisis del caso, se utilizará información correspondiente a una operación minera de cobre del norte de Chile al interior de Antofagasta, donde se efectuaron pruebas con ampliación del diseño de perforación al incorporar un nuevo explosivo de mayor potencia.
El desarrollo de las pruebas consistió en comparar el uso del nuevo explosivo (Vertex) con el utilizado en la línea base (Blendex), medir el resultado granulométrico y a partir de ello, generar una proyección de la ampliación del diseño de perforación conservando los resultados granulométricos.
La zonificación de la mina es por medio de unidades geo-litológicas y en este caso se analizará la unidad geotécnica N°4 (UGT-4) correspondiente a un pórfido argílico de la fase N°1. La información obtenida y los parámetros de diseños utilizados, se resumen en la siguiente tabla:
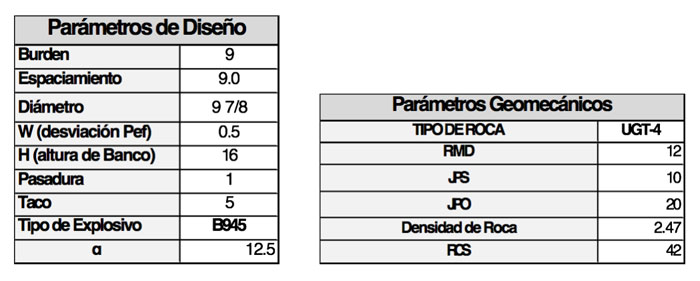
Los resultados comparativos se pueden apreciar en la siguiente tabla, resultando en una disminución de la fragmentación en un 10.4% para el 80% pasante del material fragmentado:
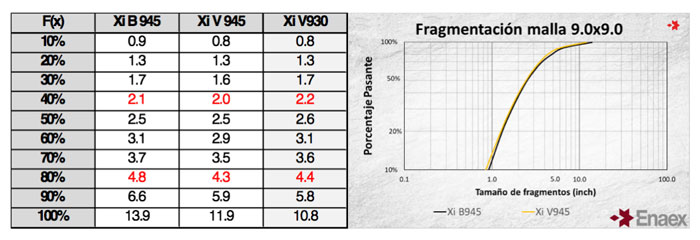
Ajuste de la curva de fragmentación
La metodología de ajuste se basa en minimizar la sumatoria del error resultante de la comparación de la curva real versus la curva ajustada mediante la utilización de la herramienta Solver de Excel. Los resultados se muestran a continuación:
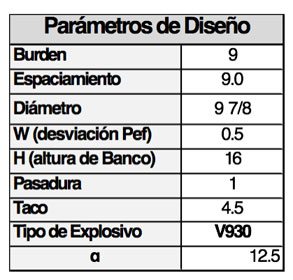
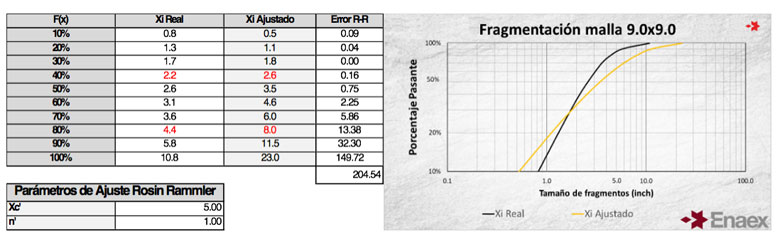
Donde Xi está ajustado en relación con el siguiente formulismo:
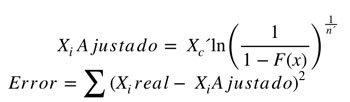
Donde en primera instancia para Xc´ y n´, se utilizan valores de 5 y 1 respectivamente como referencia inicial.
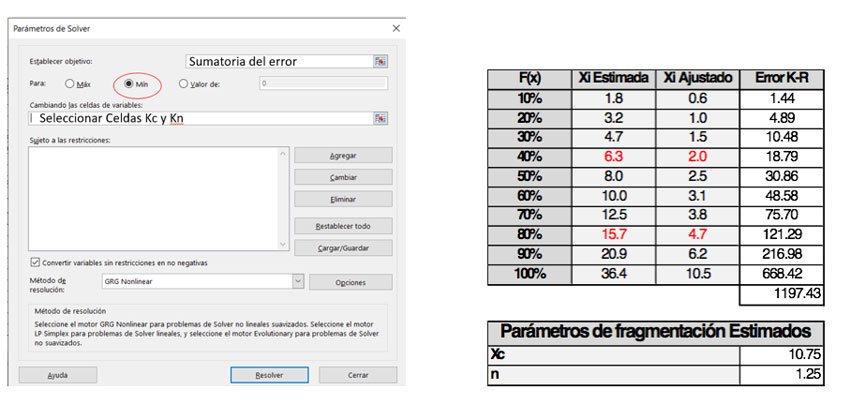
La utilización de Solver nos ayuda a encontrar los parámetros Xc´ y n´ de forma iterativa, minimizando el error al seleccionar la celda de la sumatoria, modificando las variables Xc’ y n’ como se muestra a continuación:
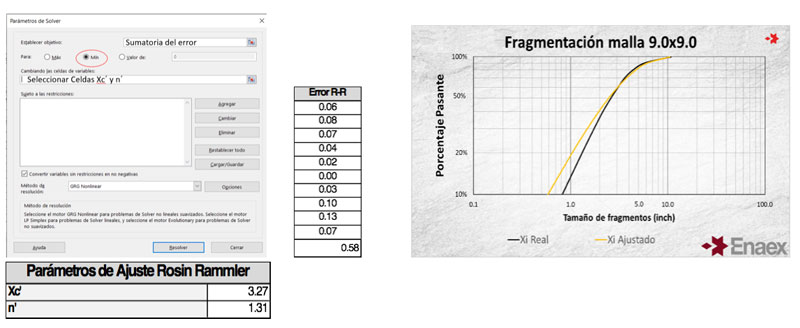
Ajuste del Modelo de Predicción de Fragmentación
La estimación del modelo Kuz-Ram, se puede visualizar en el siguiente gráfico (Xi Estimado):
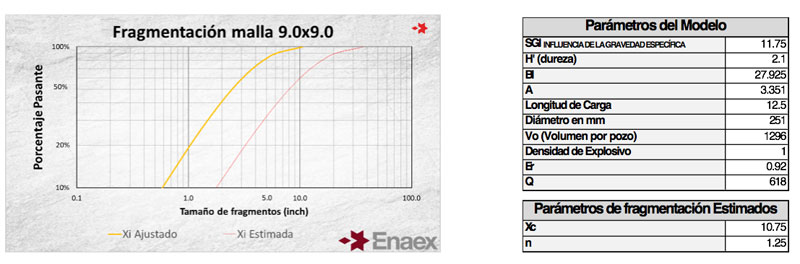
La diferencia que refleja el modelo es posible ajustarla mediante dos factores Kx y Kn, los cuales estarán asociados a la unidad geotécnica analizada, donde Kx es una constante que ajusta los parámetros asociados a la roca en función del comportamiento de fragmentación del macizo rocoso, y Kn es una constante que ajusta el comportamiento de uniformidad de la fragmentación del macizo rocoso asociado a la UGT correspondiente (para este caso UGT-4). Los factores de ajustes se incorporan de la siguiente forma en la ecuación del modelo de predicción de Kuz-Ram.
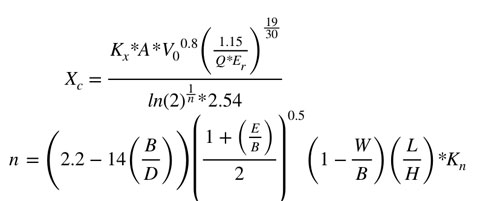
Para encontrar estos factores, es necesario utilizar la herramienta Solver, de igual forma como fue ajustada la curva de fragmentación real, pero esta vez el error considera la diferencia entre el Xi Estimado y el Xi Ajustado, como se muestra en la siguiente ecuación:
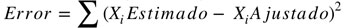
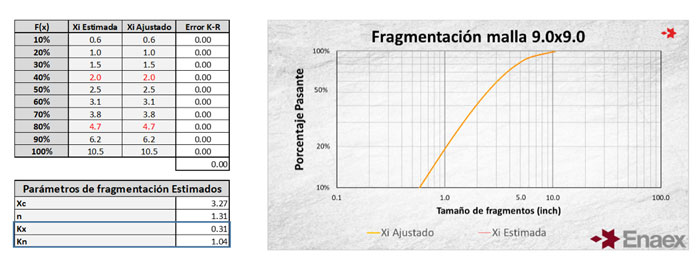
En el gráfico se puede observar que la curva estimada de Kuz-Ram se iguala a la curva ajustada Rosin-Rammler al utilizar los factores Kx y Kn, debido a que ambos están desarrollados bajo el mismo modelo.

Desarrollo de un Formulismo de Burden en base al Requerimiento de Fragmentación
Con el modelo ajustado, podemos obtener un mayor grado de precisión en la predicción de fragmentación. Luego, para obtener los parámetros de diseño en función de una granulometría deseada, es posible despejar el Burden de la ecuación de forma parcial, quedando una formula iterativa. Para ello se debe dejar todas las variables en función del Burden, como se muestra a continuación:
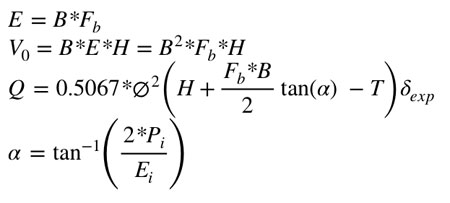
Siendo:
- Fb: Factor de relación entre Burden y Espaciamiento
- P: Pasadura (m)
- Pi y Ei: Pasadura y Espaciamiento de los parámetros de diseño iniciales que ajustaron la curva real de fragmentación
- a: Es el ángulo medido desde el fondo del pozo y el punto medio del espaciamiento a nivel del banco, el que mide el grado de comportamiento del macizo rocoso en cuanto al corte horizontal, permitiendo medir la pasadura necesaria de la perforación al realizar una modificación del espaciamiento entre perforaciones que inicialmente se tenía calculado y calibrado. Este ángulo varía entre 10 y 30 grados dependiendo de las estructuras del macizo rocoso y las tensiones residuales (teoría del cono invertido de López Jimeno).
Al igualar las ecuaciones de Xc, obtenemos los siguiente:
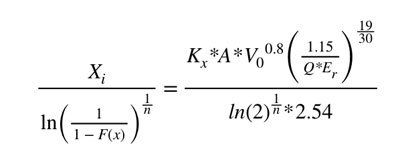
Agrupando y reemplazando los términos, podemos obtener una fórmula iterativa de Burden:
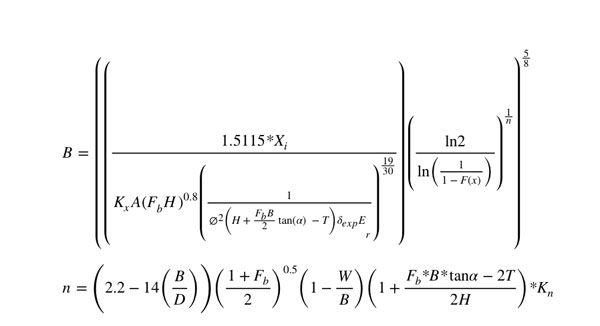
Realizando los cálculos en base a los resultados anteriores, los parámetros sugeridos de Burden, Espaciamiento y Pasadura son presentados en la siguiente tabla:
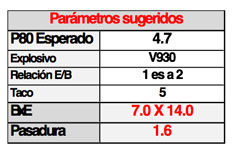
A partir de lo anterior, se propone un aumento de diseño de perforación, con una configuración de 7x14 metros y diámetro 9 7/8”, obteniendo la siguiente estimación de fragmentación:
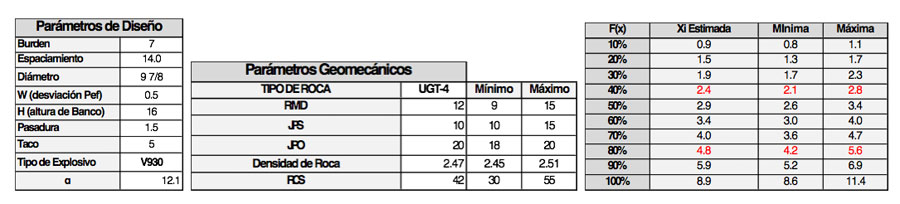
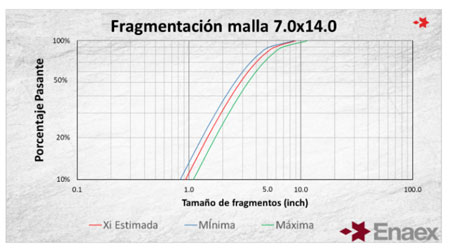
Como se visualiza en la gráfica, se puede obtener una banda de estimación ingresando el rango en que oscilan los parámetros geomecánicos.

Resultados
De las pruebas de campo se obtuvieron los siguientes resultados que se presentan en la tabla a continuación:
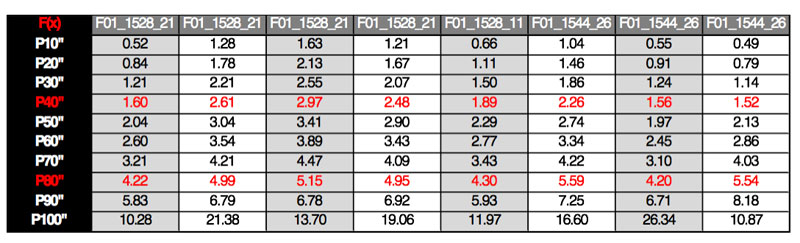
El promedio ponderado del P80 corresponde a 4.8” con una desviación estándar de 0.57 pulgadas. La curva de fragmentación promedio ponderado por el tonelaje de cada tronadura, se presenta en la siguiente gráfica:
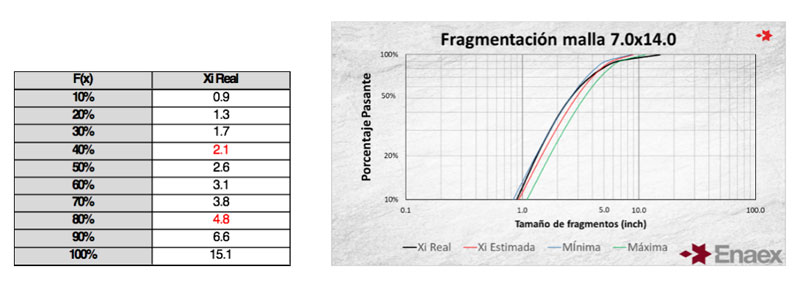
Conclusiones
Con los resultados obtenidos, es posible verificar que el método de ajuste y formulismo de Burden utilizados, son validados para obtener el resultado bajo una fragmentación requerida.
Se debe tener en cuenta que la precisión del ajuste del modelo predictivo dependerá de la variación de los parámetros geotécnicos con que se encuentra zonificada la mina, ya que en algunos casos puede llegar a presentar variaciones relevantes, debido a la presencia de alteraciones y carbonatos en el macizo rocoso, los que pueden presentar un resultado de fragmentación más gruesa, debido al grado de plasticidad que estas propiedades le confieren a la roca.
La confiabilidad de los datos es fundamental para poder generar un mejor ajuste, por lo que una mayor captura de información nos ayudará a precisar de mejor forma el modelo.
Finalmente, con esta metodología podemos construir un modelo predictivo de fragmentación ajustado por cada zonificación de la mina o unidad geotécnica, determinando factores de ajustes (Kx y Kn) individualizados, lo que nos ayudará a predecir nuestros resultados de fragmentación optimizando los recursos al calcular rápida y directamente una configuración de diseño de perforación en base a una granulometría deseada por medio del formulismo de Burden planteado.
Referencias:
[1] López Jimeno, Carlos. Manual de perforación y voladura de roca. 3. Ed. Instituto Tecnológico Geominero de España: ITGE, 1994.
[2] Enaex SA, Manual de Tronadura, enero 2011.
[3] Mundaca Muñoz, Oscar. Estudio, análisis y mejoras para lograr una granulometría adecuada en los procesos de perforación y tronadura de una minera con depósitos tipo estratoligados. Antofagasta, 2014. Tesis – Facultad de Ingeniería, Universidad Antofagasta Chile.






















































