Estudio pospandeo de placas de materiales compuestos en paneles aeronáuticos
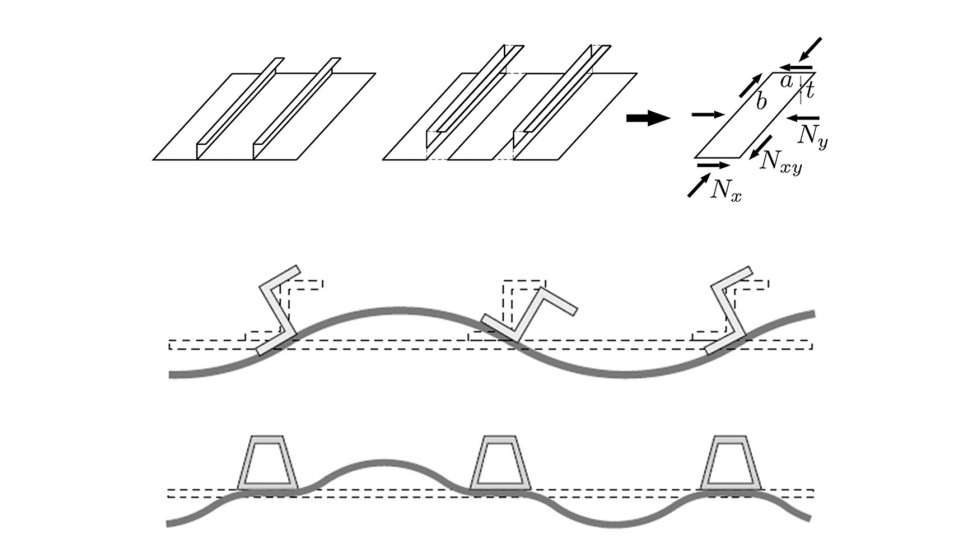
Un buen diseño de la secuencia de pandeo de cada uno de los elementos que conforman un panel es crucial para obtener una estructura resistente y ligera. El primer modo de pandeo deseable en un panel es el local de la piel, es decir, el pandeo de placas finas situadas entre los larguerillos. Este modo permite a la piel trabajar en elevados regímenes de pospandeo redistribuyendo la carga hacia los rigidizadores laterales y aportando así gran resistencia a la estructura. Por otro lado, inicialmente el pandeo a flexión del panel o el pandeo global de los larguerillos (rigidizadores longitudinales) se deben evitar, pues este efecto implicaría una sobrecarga de los paneles adyacentes en la estructura que derivaría a un fallo catastrófico. Si se produce un fallo en la piel o en un larguerillo, el panel no vería limitada tan severamente su capacidad para aguantar carga sin sobrecargar los paneles adyacentes. Esta capacidad de trabajo de los paneles después del pandeo de la piel se puede observar en la figura 1.

Dependiendo del tipo de rigidizador (y las relaciones generales de espesores) que incorpore el panel se tendrán diferentes condiciones de contorno así como diferentes solicitaciones en la placa a analizar. Para larguerillos con baja rigidez torsional como son los de sección abierta, la piel podrá girar libremente como si de una articulación se tratara (figura 2), mientras que los larguerillos con secciones con alta rigidez a torsión forzarán a la piel a permanecer recta en sus extremos, es decir, aproximándose a conseguir una pendiente nula como en un empotramiento.
1. Pandeo inicial de placas
Antes de estudiar la placa en régimen de pospandeo, es necesario estimar su carga crítica de inicio de pandeo a través de métodos basados en la minimización de la energía total Π = UD+ W, suma de la interna y de las cargas externas (Ecs. 1). Un método analítico aplicable es el de Ritz y otro numérico el de los Elementos Finitos (MEF).
En la figura 3 se presentan los resultados de carga de inicio de pandeo para una placa articulada sometida a compresión Nx y a cortante Nxy por sendos métodos. Estas cargas críticas se calculan empleando un algoritmo basado en perturbaciones lineal que proporcionaba las cargas mismas y el modo asociado (problema de autovalores en terminología matemática).
Cabe destacar la influencia del número de términos empleados para hallar la carga crítica mediante Ritz (Ec. 3). Se puede inferir cómo en placas cuya relación de aspecto de lados es aproximadamente cuadrada a/b < 1,5, la solución con un término no presenta gran desviación respecto a soluciones más precisas como puedan ser las de 16 términos o con MEF. Los picos que se observan en las curvas de la figura indican el cambio de modo de pandeo, es decir, en una placa cuya relación de aspecto sea inferior a 1,5, el modo presentará una sola semilongitud de onda en dirección de la aplicación de la carga.
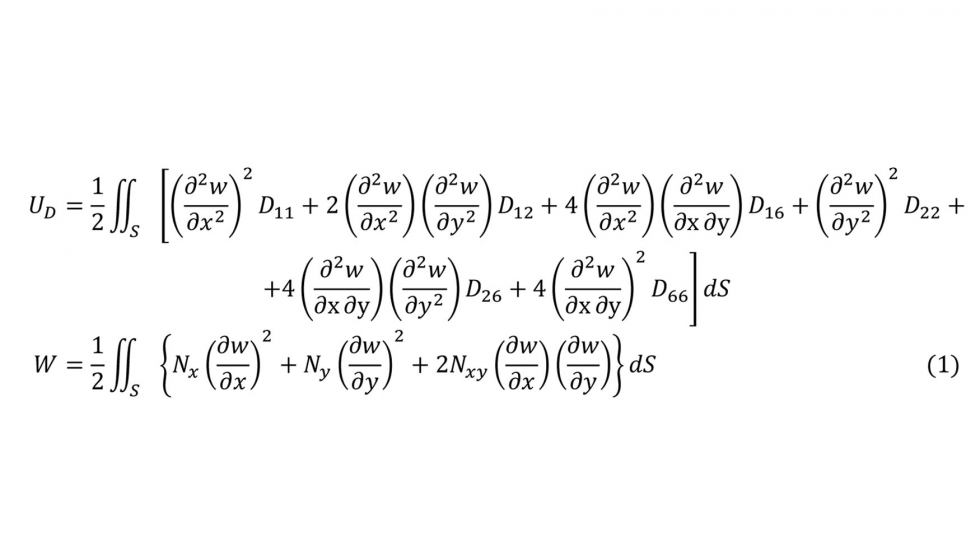
![Figura 3. Curva envolvente inicio de pandeo adimensionalizada en un laminado [0/90/±45]s Figura 3. Curva envolvente inicio de pandeo adimensionalizada en un laminado [0/90/±45]s](https://img.interempresas.net/fotos/1325807.jpeg)
2. Pospandeo de placas. Solución analítica
2.1. Bases teóricas
Las placas rigidizadas en sus bordes poseen una gran capacidad de soportar carga adicional después de pandear por primera vez, y es esta propiedad la que las hace atractivas en el diseño de estructuras ligeras como las aeronáuticas. La deflexión después de un cierto nivel de carga no es directamente proporcional al incremento de dicha carga, sino que aumenta más lentamente, permitiendo soportar un régimen de pospandeo antes de que los momentos flectores se tornen críticos. Esta capacidad extra se debe a que los lados de la placa están restringidos a deflexión y en la mayoría de los casos obligados a permanecer rectos.
Se desarrollarán deflexiones importantes que sobrepasarán su espesor, además, en dichas condiciones la energía de deformación debida a la extensión del plano medio y las fuerzas de membrana que se originarán no podrán ser despreciadas. Por tanto su estudio está fuera del ámbito de la teoría de pequeñas deformaciones y de las hipótesis de Kirchoff habituales en flexión de placas finas. El plano medio ya no permanece inextensible durante la flexión de la placa que está pandeando y se debe usar la teoría no lineal de gran o media deformación, experimentando cada punto del plano desplazamientos u0= u, v0= v, w en los ejes x, y, z, respectivamente. La deflexión w es grande por lo que es necesario conservar los términos de la pendiente al cuadrado y las relaciones cinemáticas del plano medio se transforman en expresiones no lineales:
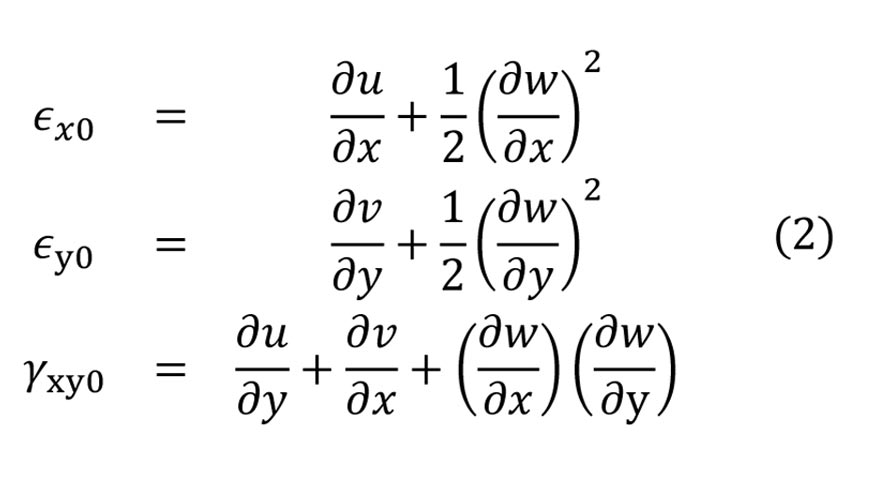
Estableciendo el equilibrio diferencial en una placa y aplicando las suposiciones y relaciones anteriores, se llega a dos ecuaciones conocidas como de von Karman, que rigen el comportamiento pospandeo de una placa en grandes deflexiones y que se presentan a continuación para un laminado simétrico (Bij= 0). La ecuación 3 describe el comportamiento a flexión de la placa y su acoplamiento con las solicitaciones en el plano (equilibrio). La ecuación 4 relaciona el comportamiento de membrana de la placa con las curvaturas fuera del plano (compatibilidad).
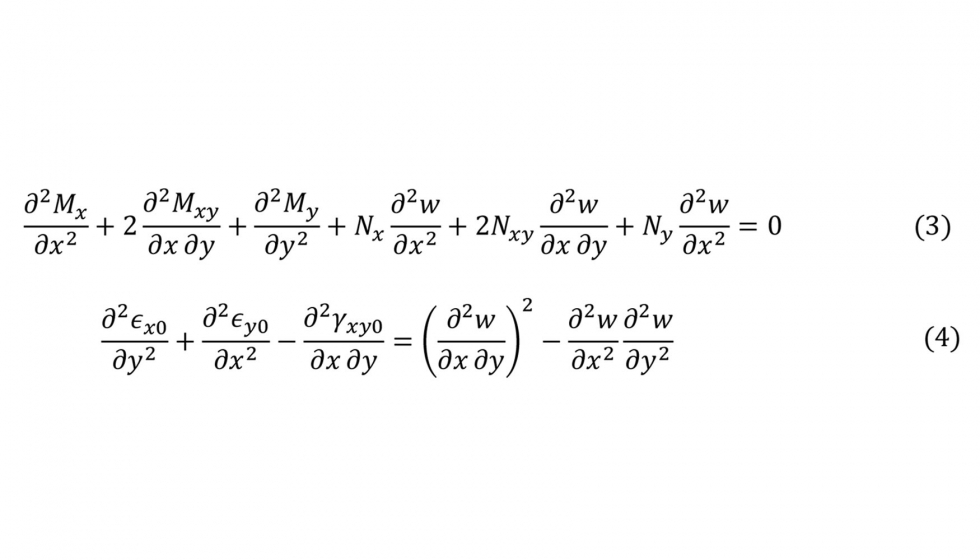
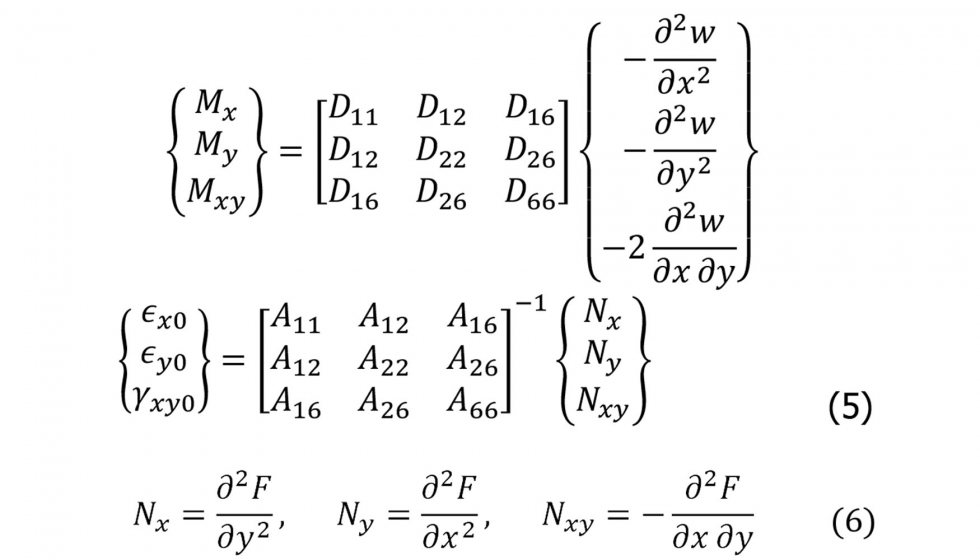
2.2. Resolución para placa articulada a/b < 1,5
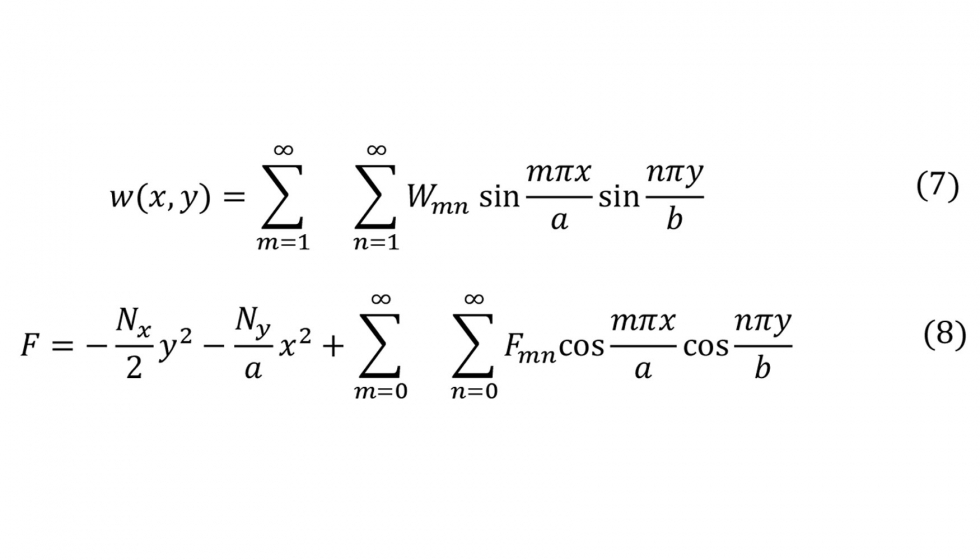
A lo largo de esta sección se desarrolla una solución de las ecuaciones de von Karman para una placa totalmente articulada sometida a compresión cuya relación de aspecto es a/b < 1,5, es decir, para placas casi cuadradas cuyo primer modo de pandeo sea una semilongitud de onda en dirección de la aplicación de la carga. Para ello se usa funciones de prueba tanto para la deflexión w como para la carga aplicada, esta última a través de la función de tensiones de Airy F, ecuación 8. La función es un sumatorio de series trigonométricas de coeficientes indeterminados que cumplen las condiciones de contorno impuestas en una articulación. Para w se asume la función de prueba en series de función seno, ecuación 7.
En régimen de pospandeo, se diferencia en tipo de placas según la condición de los bordes descargados (figura 4):
a) Rectos e inmóviles.
b) Rectos pero con libertad de traslación en v.
c) Sin restricción al movimiento en v ni necesidad de permanecer rectos.
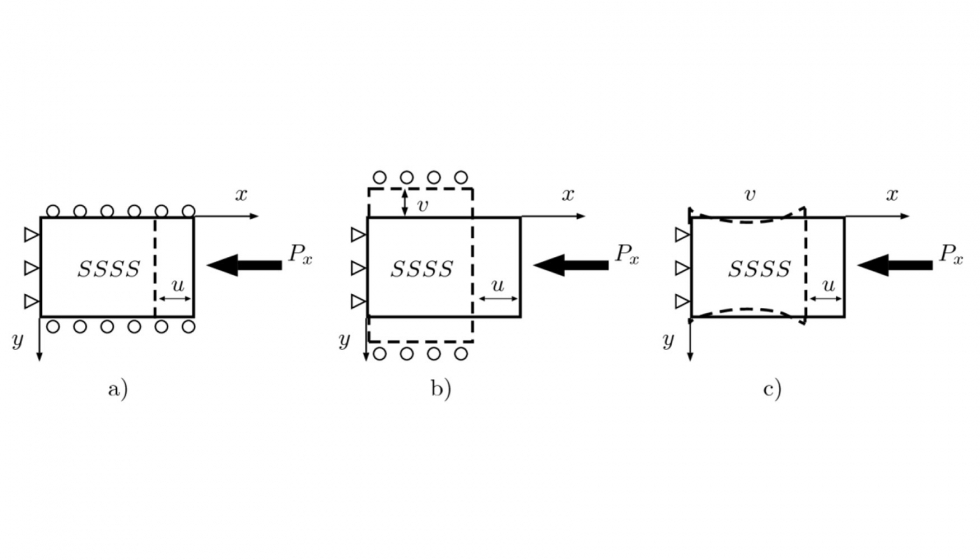
La solución analítica de pospandeo prueba una función en forma de series de una placa articulada bajo compresión uniaxial con los bordes no cargados tipo a) y c), para diferentes tipos de laminados simétricos. Se ha empleado un solo término en la función de prueba de la deflexión para que se represente correctamente el modo de pandeo (Ecuación 9) y dos en la de la tensión para capturar la variación de esa tensión en los bordes (Ecuación 10).
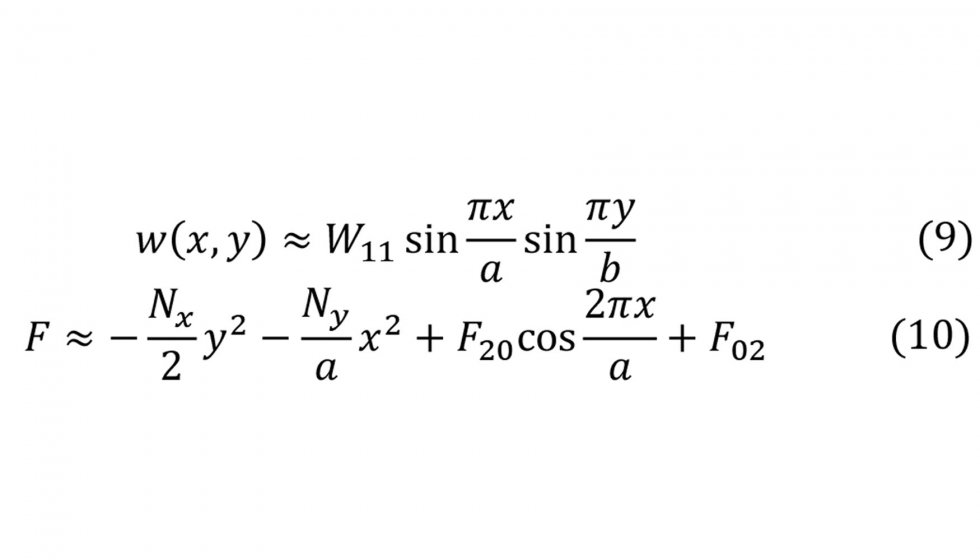
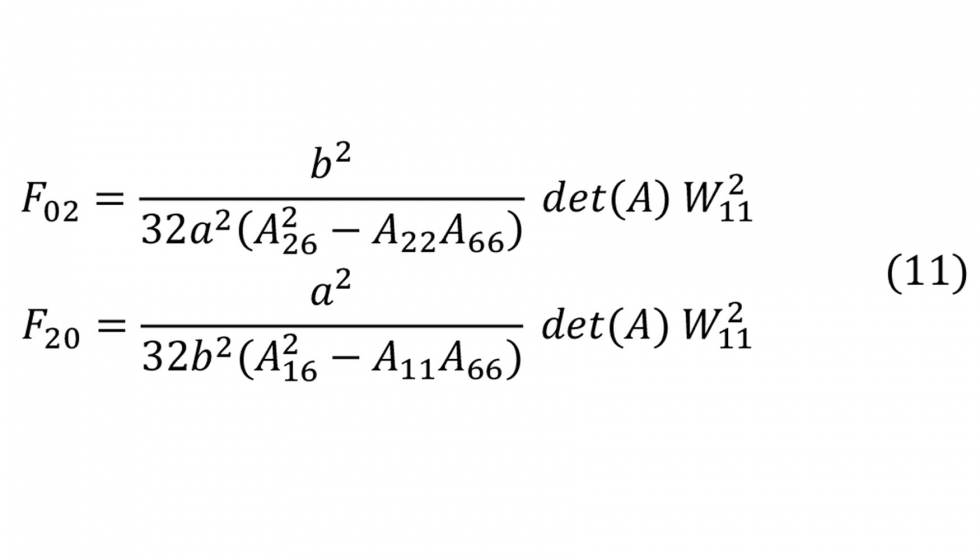
2.3. Placa con bordes descargados que permanecen rectos
Para este tipo de placa se han obtenido tres soluciones W11, es decir, del coeficiente indeterminado de la expresión de deflexión en la ecuación 9. En la primera ecuación 12 se presenta el modelo para un material isótropo, en la segunda para un laminado simétrico Bij= 0 que además no presenta acoplamiento entre extensión y deformación angular A16 = A26 = 0 ni acoplamiento flexión torsión D16= D26= 0. Finalmente, en la tercera Ec. 12 se presenta el modelo de deflexión para un laminado simétrico cuasi-isótropo. En la figura 5 se representa la deflexión de la última expresión para varios valores de Nx/Ncr. Para ratios unidad o menores obviamente no hay deflexión.

![> Figura 5. Deflexión pospandeo para laminado T300/epoxy [0/90/±45]s. Placa articulada con bordes descargados que permanecen rectos... > Figura 5. Deflexión pospandeo para laminado T300/epoxy [0/90/±45]s. Placa articulada con bordes descargados que permanecen rectos...](https://img.interempresas.net/fotos/1325817.jpeg)
2.4. Placa con bordes descargados que permanecen libres
Mediante el mismo procedimiento, pero en este caso permitiendo libertad de desplazamiento en los bordes descargados, se obtienen las soluciones para el coeficiente W11 de la expresión de la deflexión y para los tres tipos de apilamientos anteriores. Curiosamente los resultados son iguales excepto por el factor 3 que multiplica a a4 en los denominadores, que se convierte en 1.
![Figura 6. Deflexión pospandeo para laminado T300/epoxy [0/90/±45]s. Placa articulada con bordes descargados que permanecen libres... Figura 6. Deflexión pospandeo para laminado T300/epoxy [0/90/±45]s. Placa articulada con bordes descargados que permanecen libres...](https://img.interempresas.net/fotos/1325818.jpeg)
En la figura 5 se representa la deflexión de la última expresión para varios valores de Nx/Ncr. Nótese que debido a la menor restricción de los apoyos no cargados.
3. Pospandeo de placas. Solución MEF
3.1. Algoritmo de resolución MEF
Realizar un estudio de pospandeo con MEF requiere del uso de procedimientos no lineales. La metodología para estudiar el pospandeo cambia con respecto al inicio de pandeo y requiere de una serie de pasos e interpretaciones que se describen a continuación y se pueden visualizar en el diagrama de flujo representado en la figura 7.
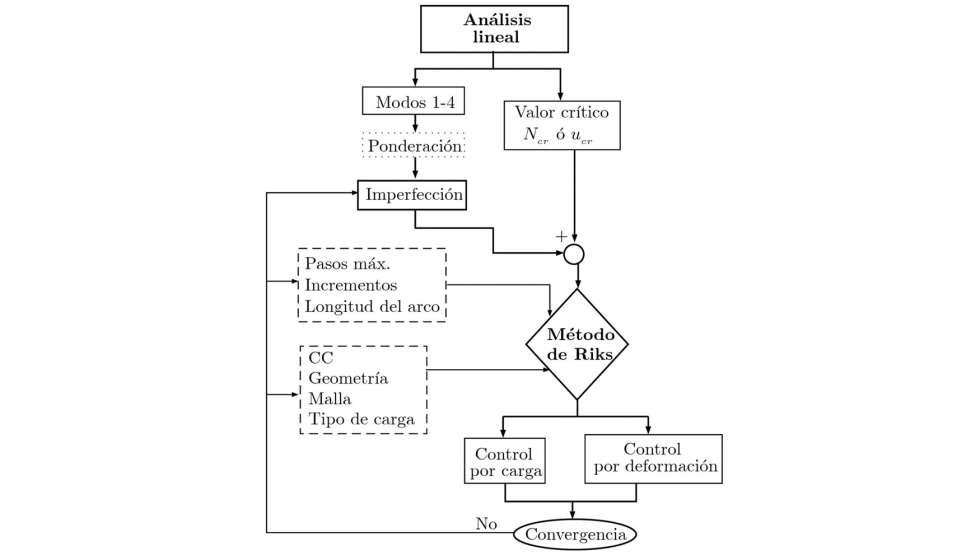
1. En un archivo separado se efectúa una perturbación lineal como la realizada en los primeros análisis, con el fin de obtener el valor crítico de inicio de pandeo y los cuatro primeros modos. El valor crítico puede ser o bien la carga crítica de pandeo, Ncr si se hace un control por carga, o bien el desplazamiento crítico de pandeo, ucr, si el control es por desplazamiento. Los datos que describen los modos se escriben en un fichero.
2. Se crea un nuevo trabajo, esta vez estableciendo el método de Riks modificado (También conocido como control por longitud del arco) como algoritmo de resolución e introduciendo a la geometría una serie de no linealidades en forma de imperfecciones provenientes del análisis anterior. Las imperfecciones son los cuatro modos obtenidos del análisis lineal, a los que se le ha de aplicar una ponderación que normalmente es diez veces menor que el orden de magnitud del espesor de la placa para el primer modo y algo inferior para otros tres, como regla general. Para placa de espesor t:
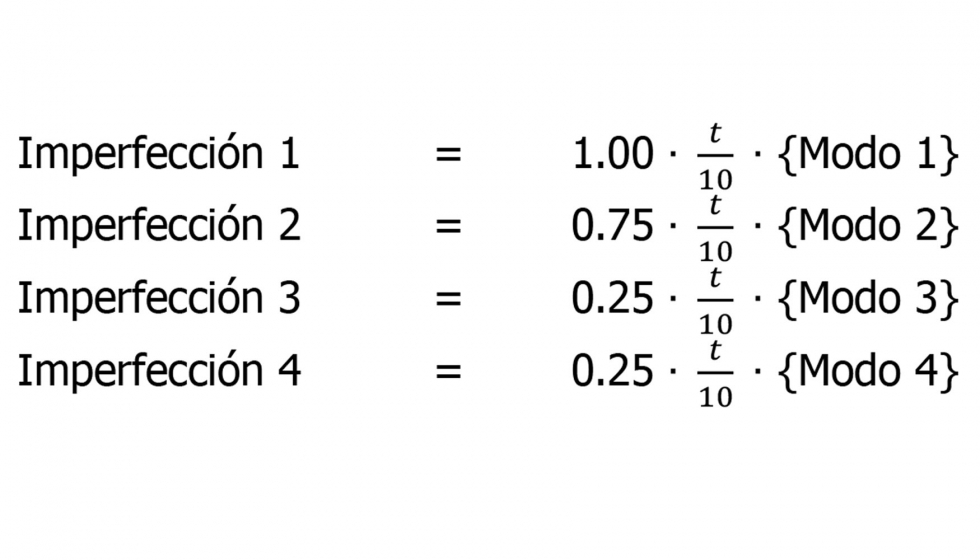
1. Con las imperfecciones ‘sembradas’ se ha de fijar el valor crítico a partir del cual se inicia el pandeo, que como se ha dicho en el punto 1 puede ser la carga crítica o la deformación crítica y el valor máximo de ratio de carga de pospandeo que se quiere alcanzar, normalmente Nx/Ncr < 8, ó ux/ucr< 8, con número máximo de 500 pasos.
2. A partir de la asignación del valor crítico, se inicia el algoritmo de cálculo por longitud del arco, aplicando incrementos de carga (o deformación) respecto al valor inicial (Ncr ó ucr) y obteniendo las salidas requeridas (de tensiones, deformaciones...) en cada paso. Los incrementos de carga varían según el paso, fijándose en este trabajo un máximo de 10 y un mínimo de 0,01.
3. Si el cálculo converge, en el post-procesado se revisa la curva que muestra la evolución del ratio Nx/Ncr. Si la intestabilidad se produce para Nx/Ncr = 1 o para un valor muy cercano (la curva pierde linealidad en este valor), el resultado es satisfactorio. Si por el contrario la inestabilidad de la placa se inicia lejos de Nx/Ncr = 1, se usa una de las tres opciones:
a) Establecer nueva ponderación de modos que siembran las imperfecciones.
b) Cambiar el control de carga a desplazamiento o viceversa.
c) Revisión de las condiciones de contorno aplicadas.
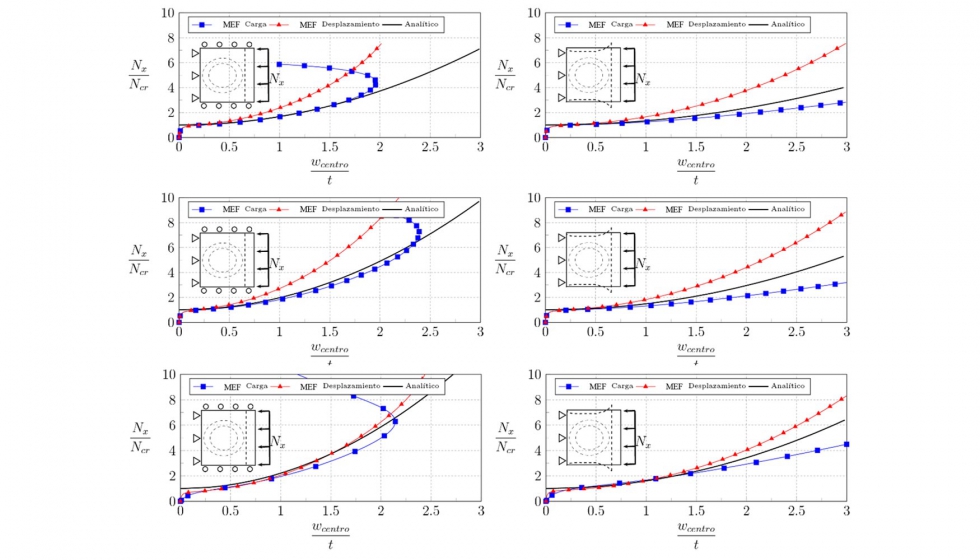
En las figuras 10 se muestran gráficas la deflexión del centro de la placa en función del ratio de pospandeo Nx/Ncr, obtenida con el modelo analítico derivado de las ecuaciones von Karman y con simulación MEF mediante control por carga y por desplazamiento.
Para una placa de aluminio isótropa, se aprecia en la primera (de izquierda a derecha y de arriba a abajo) figura 10 cómo el modelo analítico propuesto concuerda con el control por carga efectuado con el de MEF hasta el ratios de pospandeo próximos a 3. Para este valor se capta un cambio de modo de pandeo desde una semilongitud de onda a una onda completa, escapando fuera del rango del modelo analítico. El control por desplazamiento sin embargo, sobreestima la de flexión que alcanza la placa y no captura el cambio de modo, no siendo tan efectivo como el de carga.
En la segunda figura 10 se ha representado la misma placa pero con los bordes descargados libres. Para este caso, la correlación entre el modelo analítico y el control por carga es menos efectiva. Sin embargo se comprueba como la placa anterior tiene a deflectar menos que esta, por carecer de tensiones de compresión generadas por la restricción.
Para un laminado simétrico, en el que no hay acoplamientos flexión-torsión ni extensión-distorsión, se vuelve a comprobar como el control por carga es más efectivo para la correlación con el modelo analítico, especialmente para placa que mantiene los bordes descargados rectos como se muestra en la tercera figura 10. La tendencia es la misma que en el caso isótropo para el comportamiento de la placa bajo condiciones de borde descargado libre, cuarta figura 10, es decir, no se aprecia un cambio de modo de pandeo con MEF y el modelo analítico se sitúa en medio del de control por carga y por desplazamiento, subestimándolo el primero y sobreestimándolo el segundo
Para finalizar, se simula un laminado simétrico más general donde ningún término de las matrices A y D es nulo, resultando el más interesante desde el punto de vista de aplicación aeronáutica. Para la primera condición de borde descargado, ambos controles concuerdan bien con el modelo analítico. No obstante y al contrario que ocurría en los casos anteriores, el control por desplazamiento es más fiel al modelo analítico pese a no capturar ningún cambio de modo. Sin embargo, el control por carga subestima a los otros dos pero capta el cambio de modo, ver la quinta figura.
Para el borde descargado libre, última figura 10, el modelo por control por desplazamiento también consigue una mejor correlación con el modelo analítico que el control por carga, a pesar de empezar a divergir lentamente para ratios de pospandeo superiores a 3.
Conclusiones
- El control por carga tiende a subestimar el modelo analítico mientras que el control por desplazamiento lo sobreestima.
- Cuando se modelan los bordes descargados de la placa como bordes libres, ningún modelo MEF capta los cambios de modo.
- La deflexión en el centro de la placa varía en gran medida según el modelo de borde descargado adoptado. Para un borde descargado recto esta deflexión es mayor que para uno considerado libre.
- El modelo analítico no es capaz de capturar un cambio de modo ya que se ha desarrollado solo para pandeo con una semilongitud de onda, es decir, modo simétrico de pandeo. Modelos más complicados son muy difíciles de desarrollar analíticamente.
- El control por carga con MEF y el modelo analítico propuesto presentan mayor correlación para placas isótropas y con laminado simétrico no general.
- La deflexión obtenida por el modelo analítico puede considerarse como media de la deflexión de los modelos de control por carga y control por desplazamiento en el caso de que los bordes descargados permanezcan libres.