Optimización del diseño de mesas rotatorias hidrostáticas de muy elevada rigidez y amortiguamiento
Esta metodología consiste en un flujo de trabajo a llevar a cabo cuando se deba diseñar una mesa rotatoria hidrostática, en base a las especificaciones funcionales de partida. A partir de dichas especificaciones funcionales, se calculan automáticamente los parámetros principales de diseño, tales como, el número de celdas hidrostáticas, espesor de película del fluido, rigidez y amortiguamiento en cada cavidad, etc. Una vez determinados estos parámetros, se introducen como variables de entrada en un modelo MEF de la mesa rotatoria hidrostática y, en base a unos objetivos previamente definidos de rigidez y amortiguamiento de la misma, se optimizan las dimensiones geométricas de los distintos componentes. De esta manera se consigue disminuir considerablemente el tiempo de diseño y optimización de las mesas rotatorias hidrostáticas. La metodología se ha aplicado al caso concreto de diseñar la mesa rototraslante de Sidepalsa.
1. Introducción
En la mayoría de máquinas-herramienta actuales se utilizan guiados lineales y rotatorios de rodadura y/o de fricción. Estos tipos de guiados implican en general un contacto físico entre superficies metálicas, lo que conlleva un desgaste de los componentes de dichos guiados. A medida que el desgaste se va incrementando, la repetitividad de las operaciones de mecanizado se ve comprometida, resultando en una reducción de la precisión, de la calidad del acabado y de la productividad. Además la rigidez y el amortiguamiento de estos guiados son limitados y las holguras y el rozamiento estático pueden dificultar un posicionamiento preciso, incluso cuando la máquina es nueva. La alternativa a dichos guiados de rodadura o de fricción son los sistemas de guiados hidrostáticos, tanto lineales como rotatorios, en los cuales las partes fijas y móviles de los guiados están separados por una fina lámina de aceite bajo presión. Este sistema elimina el contacto metal a metal y elimina virtualmente el desgaste porque los componentes “flotan” en una película de aceite muy fina. Adicionalmente, un sistema hidrostático presenta unos valores de rigidez y sobre todo amortiguamiento mucho más elevados que los guiados de rodadura o de fricción de las mismas dimensiones. Por último, los guiados hidrostáticos eliminan prácticamente tanto el rozamiento estático como el dinámico, así como las holguras en el sistema. El principal inconveniente para la utilización de guiados hidrostáticos, hasta fechas recientes, ha sido la dificultad de diseño, optimización, implementación y mantenimiento de los mismos. Se han realizado hasta la fecha actual un gran número de proyectos focalizados exclusivamente en cojinetes hidrostáticos radiales, y ciñéndose al análisis de una simple celda hidrostática. Por ejemplo Sharma [1] realizó una comparativa sobre el funcionamiento de celdas hidrostáticas con diferentes formas y también con distintos controladores de caudal, utilizando MEF para analizar las propiedades en las celdas hidrostáticas. Shie [2] realizó un estudio para determinar los parámetros óptimos de una celda de un cojinete radial hidrostático, tales como la localización del orificio de entrada del fluido, su diámetro y las dimensiones ideales de la celda hidrostática, utilizando MEF y un método de optimización combinando Algoritmos Genéticos y Análisis de Correlación de Gray. Sin embargo, no existen publicaciones de trabajos centrados en el diseño y optimización de una mesa rotaria hidrostática en su globalidad, en los que se tenga en cuenta el número óptimo de celdas, su interacción, la regulación múltiple de caudal, etc. En lo que respecta al modelado del fluido, Heinrichson [3] propuso un modelo matemático térmico 3D de la lubricación hidrodinámica basándose en las ecuaciones de Reynolds, para estudiar la influencia de la geometría de la celda en la capacidad de los cojinetes hidrostáticos. Novikov [4] propuso un modelo matemático de cojinetes axiales hidrostáticos utilizando ecuaciones diferenciales, para obtener las características del flujo del aceite en el interior de las cavidades, y además un criterio de optimización del diseño. En 2001 Ma. [5,6] analizaron numéricamente las características del flujo del fluido en un cojinete hidrostático anular, para distintas viscosidades y condiciones de trabajo, mediante el Método de los Elementos Finitos, obteniendo como resultado novedoso el campo de distribución de viscosidades a lo largo de la película de aceite. En 2007, Chen [7] estudió la influencia del tamaño del orificio de entrada y la geometría de la cavidad en la forma del fluido, resolviendo las ecuaciones de Reynolds y simulando numéricamente la distribución de velocidades y de presiones en la película de aceite, utilizando el Método de Elementos Finitos. Shao and Yu [8,11] realizaron, utilizando el software Fluent, una simulación numérica 3D de la película de aceite, para obtener la distribución de presiones, caudales, fuerzas de fricción y temperaturas en la película de aceite, en función del área y la profundidad de la celda y de la velocidad de giro.
El trabajo al que hace referencia el presente artículo abarca una metodología de cálculo, diseño y optimización de un cojinete axial hidrostático en su totalidad, es decir, incluyendo tanto los parámetros del fluido, como los parámetros mecánicos asociados, tales como fuerzas, rigidez, amortiguamiento, deformaciones y tensiones de las piezas estructurales. Siguiendo esta metodología se optimiza el diseño paramétrico del cojinete y las propiedades del lubricante, en base a unos objetivos que vienen dados por las especificaciones funcionales requeridas en cada caso para el cojinete axial hidrostático.
El trabajo ha sido realizado por la empresa Sidepalsa, especialistas en el diseño, la fabricación y montaje de accesorios para la máquina-herramienta, principalmente en cambiadores automáticos de herramientas y cambiadores de palés. Ha contado con la colaboración del centro de investigación Tecnalia. El proyecto ha sido cofinanciado por el Gobierno Vasco, bajo el programa de Proyectos de Desarrollo de Nuevos Productos – Gaitek.
2. Principio de funcionamiento de los cojinetes hidrostáticos
Principio de funcionamiento
El esquema básico de un sistema hidrostático se representa en la figura 1. El caudal de aceite a presión se alimenta en cada celda hidrostática, por lo que la presión en la misma se mantiene igual a la de alimentación. Debido a la diferencia de presiones entre la celda y el exterior, a lo largo de los bordes se produce un flujo de aceite que va desde la celda al exterior. Este caudal es creciente con la holgura en las superficies de los bordes (holgura del cojinete o guía: h) y con la diferencia de presiones. En el caso concreto de la figura 1, en contraposición a la celda de sostenimiento de la carga existe otra celda para compensar los posibles momentos de fuerzas debidos a descentramientos de las cargas.
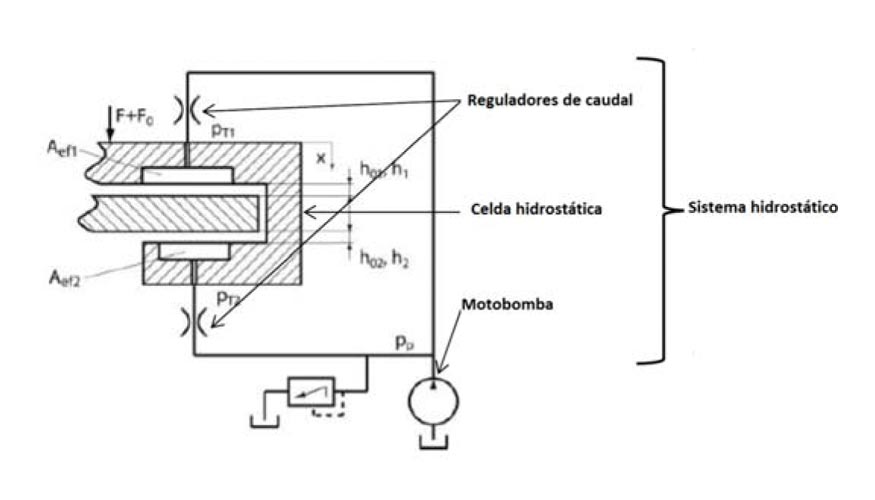
La expresión que relaciona estas variables es conocida como la ley de Hagen-Poiseuille y es la siguiente:
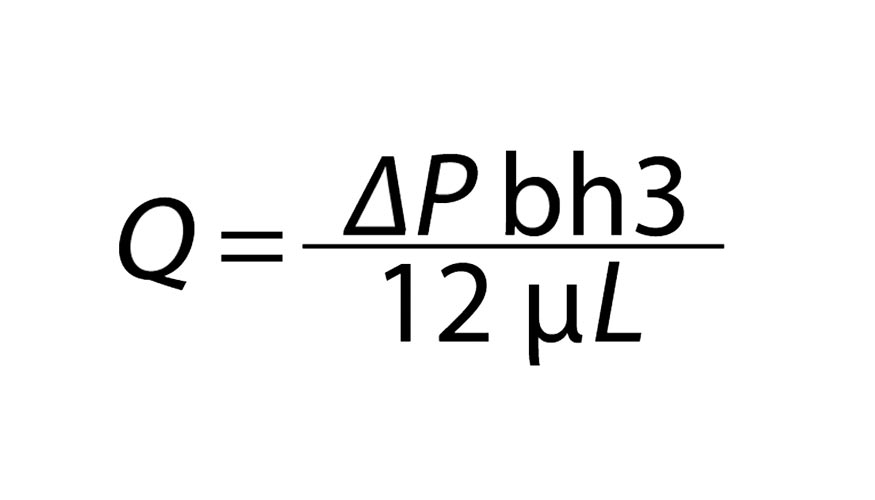
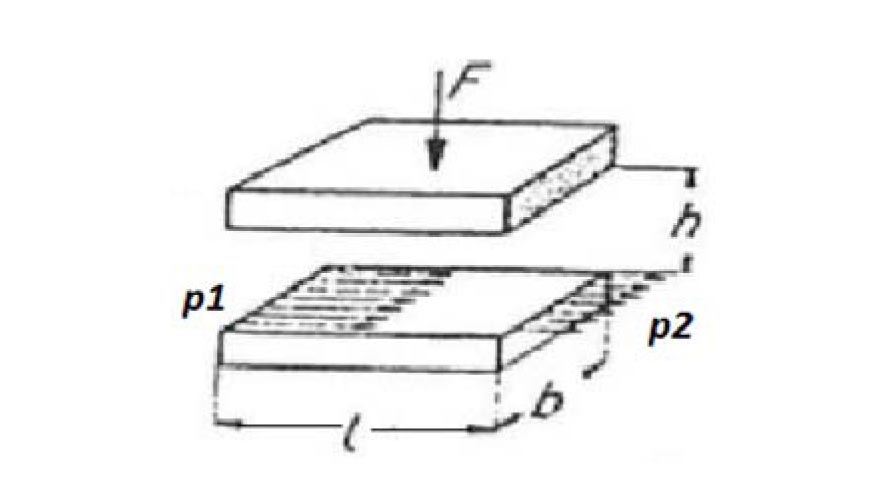
La notación de las dimensiones geométricas (b, h y L) se puede observar en la figura 2. El resto de variables de dicha expresión son las siguientes:
Δp= p1- p2 diferencia de presiones a lo largo de la longitud l.
μ=viscosidad dinámica del lubricante
La variable a controlar en el sistema es h (espesor de película de aceite). En el caso de haber cavidades de elevación (abajo en la figura 1) y retención (arriba en la figura 1), se denomina juego a la suma de ambas películas de aceite. Mantener el juego h constante garantiza la rigidez del cojinete.
Juego h= h01 (cavidad elevación) + h02 (cavidad retención).
El espesor de la película de aceite h es proporcional a la raíz cúbica de caudal entre la presión Q/P, como se puede observar al despejar la variable h en la expresión de Hagen Poiseuille. Por lo tanto, para conseguir mantener el espesor de película lo más constante posible, al existir una variación de presión debe haber una variación proporcional de caudal.
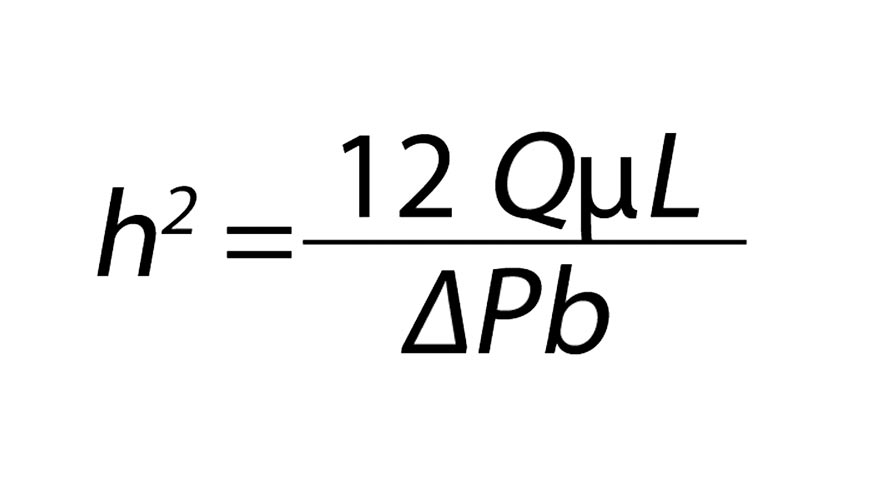
Cavidad de retención
Los cojinetes hidrostáticos pueden estar formados por celdas en la parte inferior (celda de elevación) o por celdas en la parte inferior (elevación) y en la superior del cojinete (retención). La configuración de celda de elevación + retención permite introducir una precarga F0 en las celdas, independiente de la carga estática soportada, lo que permite alcanzar rigideces mucho mayores que en los sistemas sin cavidades de retención.
La configuración de celdas de elevación + retención se recomienda cuando las cargas verticales son elevadas y están descentradas. Esto es debido a que estos sistemas pueden soportar cargas positivas y negativas y por lo tanto, colaboran con el cojinete radial (sea hidrostático o de rodadura) a la hora de soportar el momento de vuelco generado por fuerzas descentradas. Si solo hay celdas de elevación, los momentos generados por fuerzas descentradas están soportados únicamente por el rodamiento radial.
Sistemas de suministro de aceite
Con el fin de soportar cargas excéntricas, los cojinetes hidrostáticos se fabrican con varias celdas. En principio, si se quiere disponer de presiones diferentes en cada una de ellas, el suministro de aceite debe ser independiente para cada celda, de forma que se puedan absorber cargas excéntricas al conjunto. En la figura 3 se representan dos posibles soluciones a este problema:
- Utilización de una bomba por cavidad
- Utilización de resistencias hidráulicas entre la fuente de flujo hidráulico y cada cavidad.
Estas resistencias suelen materializarse en forma de tubos capilares o resistencias tipo diafragma (variables con la carga aplicada).
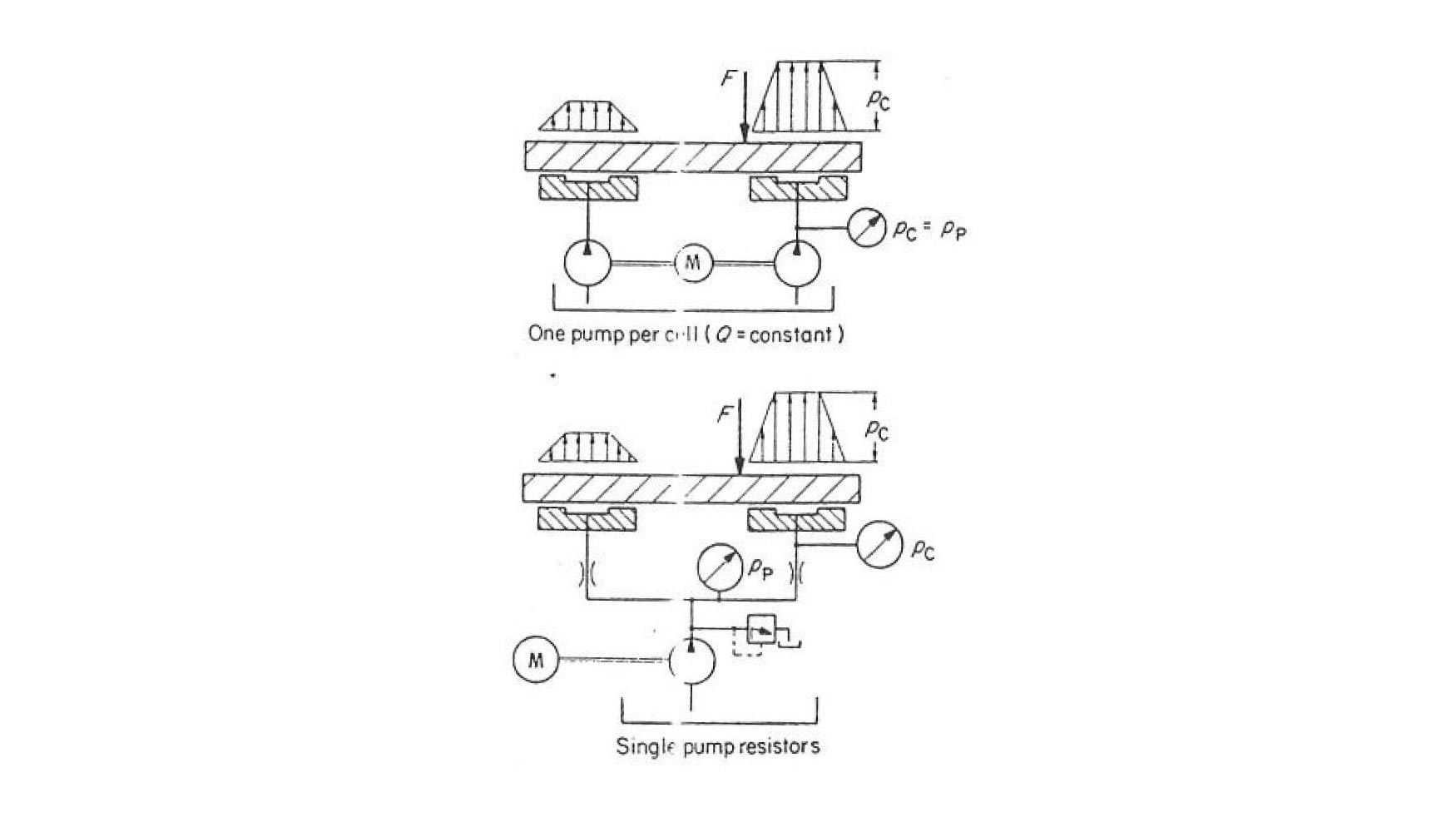
La primera solución permite una mayor capacidad de carga, ya que la misma sólo queda limitada por la presión máxima que puede proporcionar la bomba. En la segunda solución se produce una pérdida de presión en la resistencia hidráulica, proporcional al caudal que pasa por la cavidad. Sin embargo, la utilización de una bomba por cavidad supone, en general, un mayor costo e instalación y de explotación, por lo que sólo se utiliza en casos en los que se necesita un caudal muy alto y no sea suficiente con una sola bomba. La resistencia de los tubos capilares responde a la expresión:
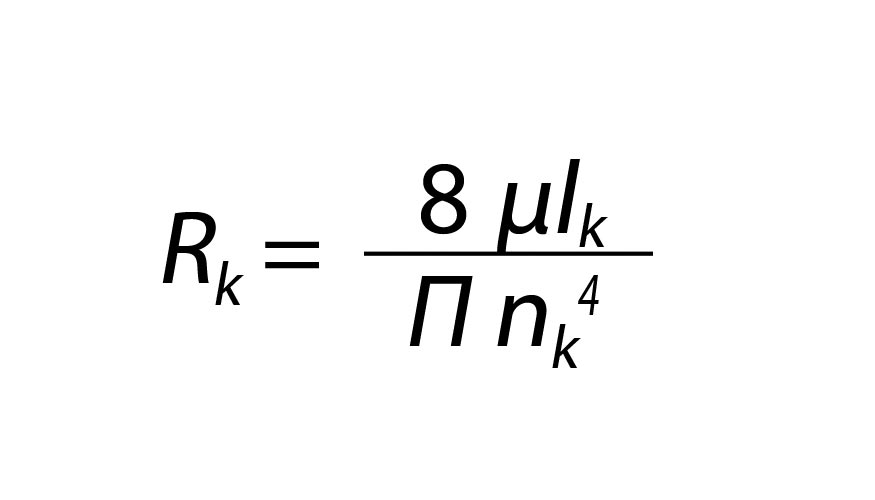
Siendo
nk = radio del tubo capilar
lk = longitud del tubo capilar
Se utilizan diferentes diseños para los tubos capilares en función de otros condicionantes de diseño. Así, se utilizarán tubos cortos con diámetro muy fino cuando se desea acomodarlos dentro de las líneas de suministro del aceite. En la parte superior de la figura 4 se muestra un diseño de este tipo.
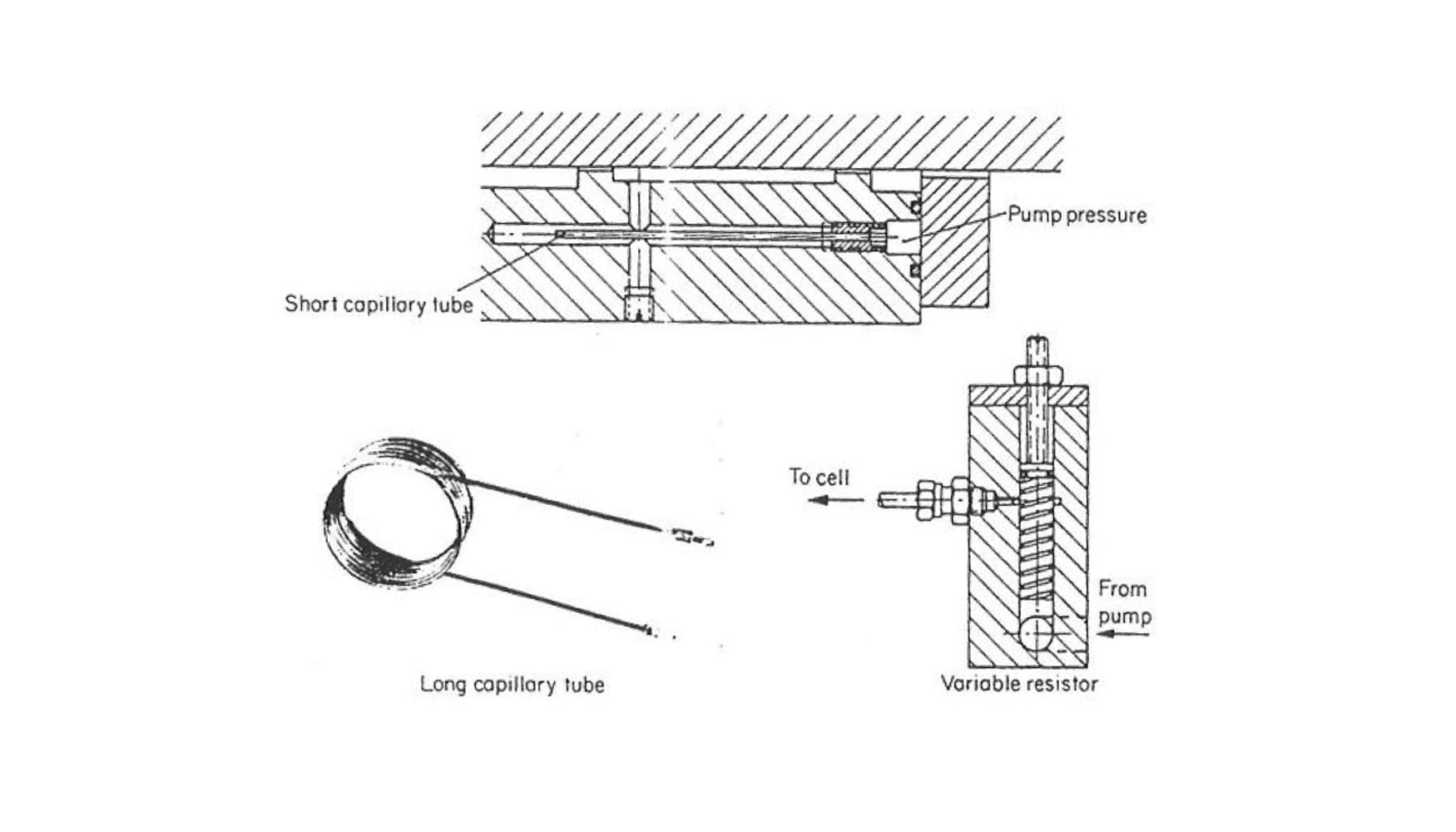
Sin embargo, la utilización de tubos de diámetro muy fino exige una gran limpieza del aceite. De hecho, el diámetro mínimo del tubo queda definido por el tamaño de las partículas que puedan encontrarse en el aceite. Diámetros mayores pueden conseguirse utilizando tubos en espiral como los indicados en la parte inferior de la misma figura. El diseño mostrado a la derecha corresponde a una resistencia que puede variarse girando el tornillo de regulación.
Junto a las resistencias constantes, existe la posibilidad de utilizar resistencias hidráulicas variables con la carga aplicada. Estas resistencias variables permiten mejorar la rigidez ya que la resistencia disminuye al aumentar la carga. En la figura 5 se incluyen dos diseños de este tipo de resistencias que han sido ideadas para garantizar una película de lubricante de altura h aproximadamente constante con cargas variables.
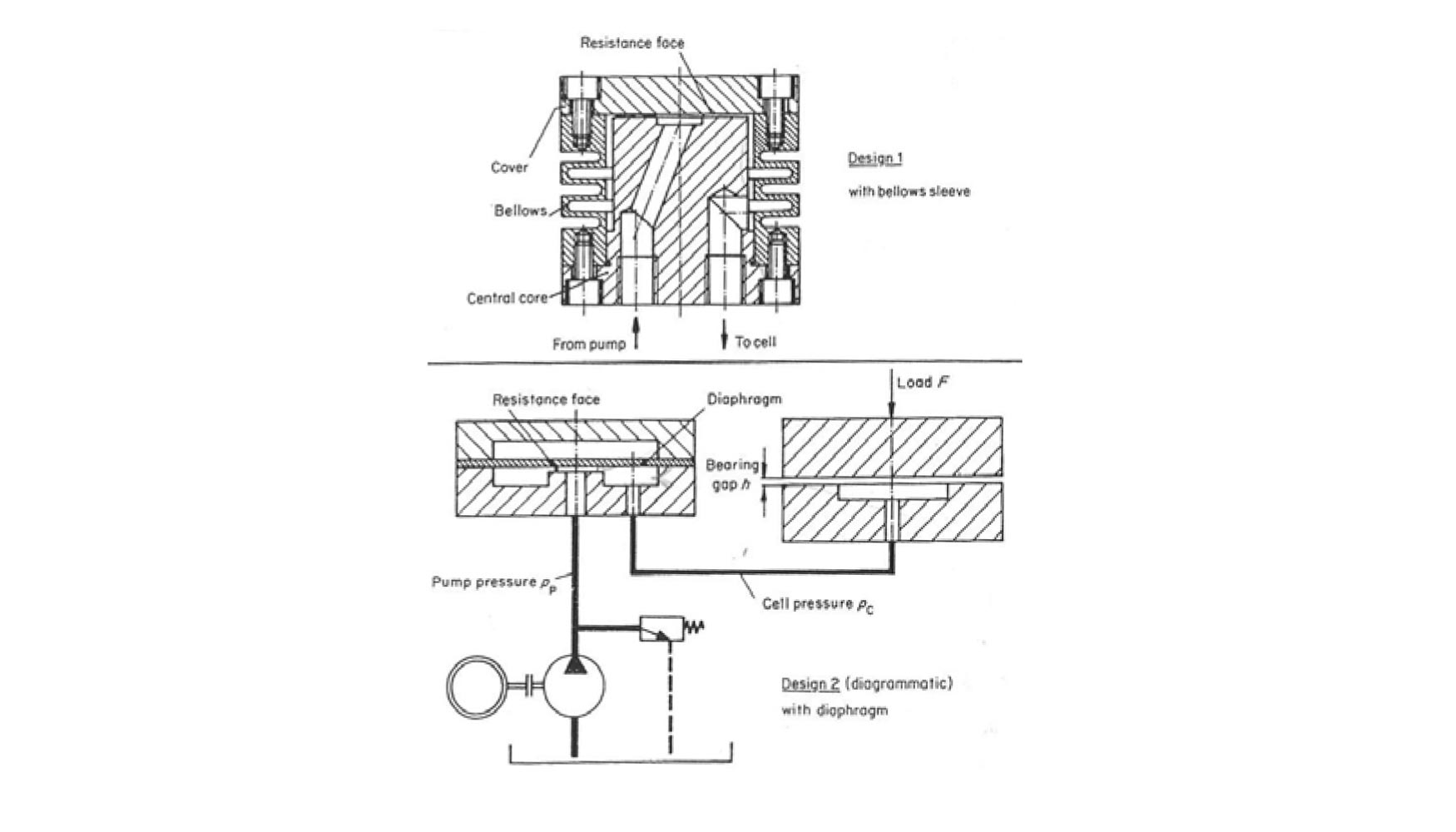
Si en la ley de Hagen Poiseuille despejamos h obtenemos:
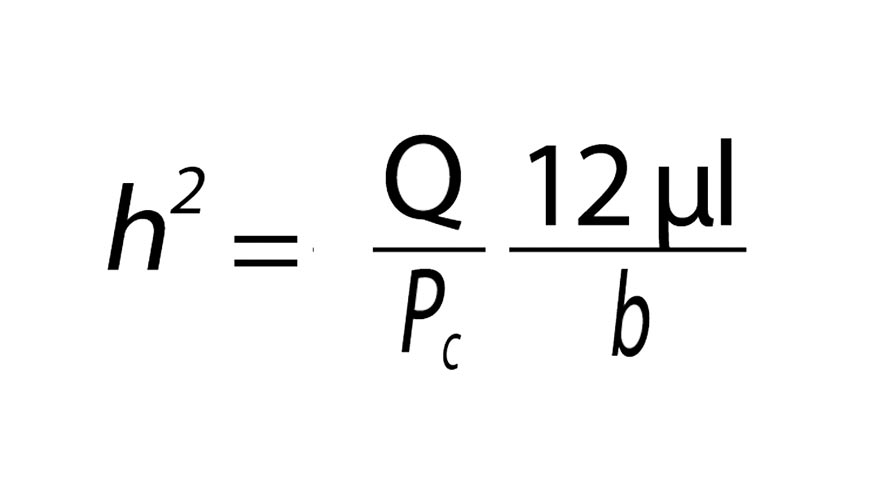
De esta expresión puede deducirse que para mantener h constante, debe aumentarse el caudal de la cavidad en proporción directa a la variación de carga. En las resistencias de la figura 6 se consigue dicho efecto, mediante la acción de la presión correspondiente a la cavidad. La presencia de esta presión controla la sección de paso del aceite, aumentando dicha sección al aumentar la presión.
En la figura 6 se muestra la variación de espesor de la película de aceite en función de la carga para tres soluciones de suministro de aceite diferentes: resistencia capilar, resistencia variable con la carga (resistencia tipo diafragma) y alimentación directa con una bomba de caudal constante.
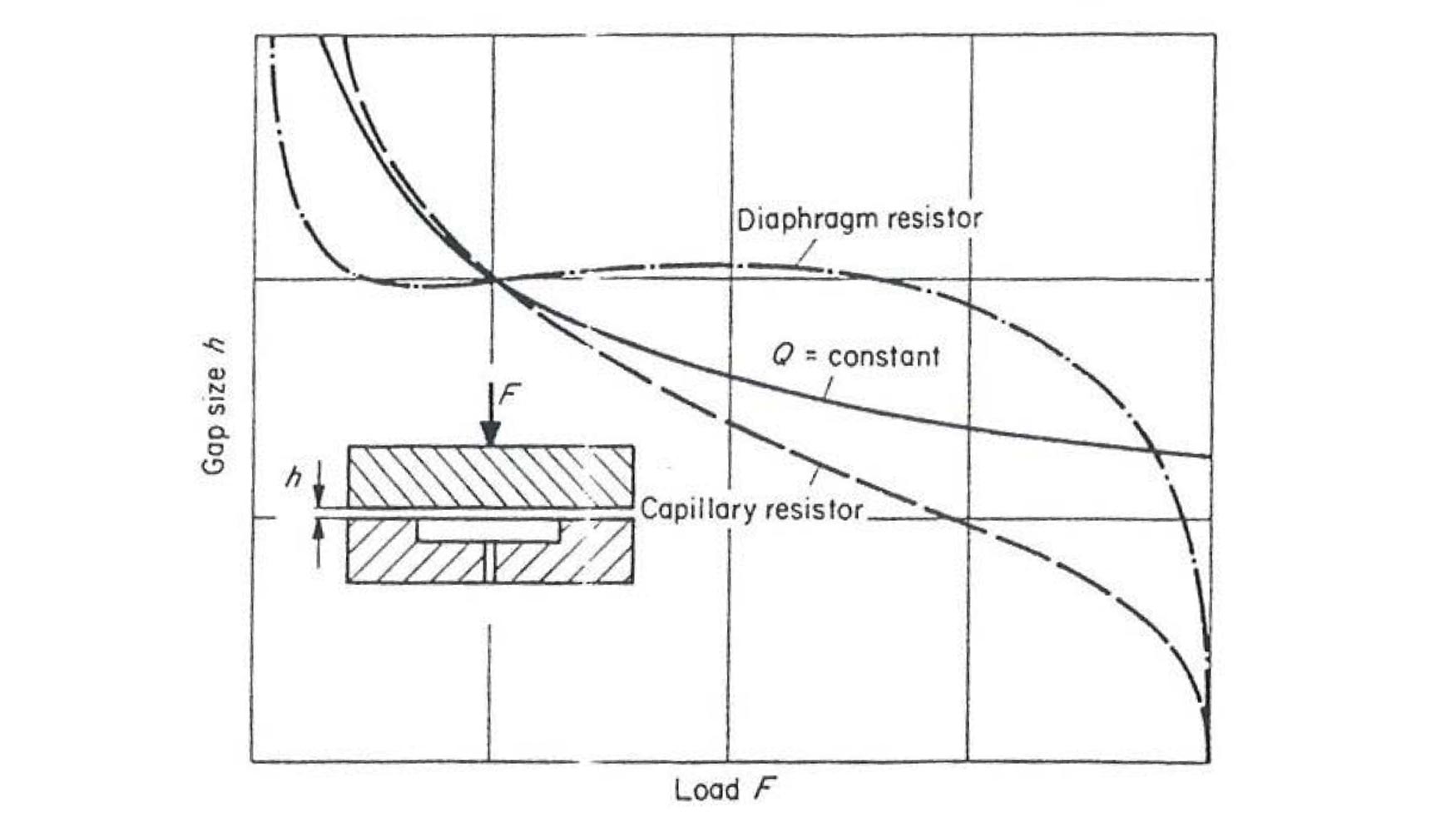
Puede observarse que la curva característica correspondiente a la resistencia tipo diafragma llega a tener un comportamiento casi ideal en un rango amplio de valores de la carga, manteniendo la altura de película de aceite aproximadamente constante. El tubo capilar da lugar a la curva más alejada de la ideal, en tanto que el sistema de caudal constante, en un rango de fuerzas intermedio da lugar a una curva comprendida entre las dos anteriores, pero para cargas elevadas proporciona una característica muy superior.
Controladores de caudal
En el diseño de la mesa rototraslante de Sidepalsa, se ha decidido apostar por la solución de controladores de flujo de la firma alemana Hyprostatik [12] para regular el caudal y la presión en las celdas hidrostáticas. Estos dispositivos son unas resistencias variables con la carga aplicada, cuyo funcionamiento se basa en una membrana metálica que por diferencia de presión regula el paso del caudal de aceite para mantener la película de aceite h constante. Se trata de un sistema auto-regulado, que no necesita de mediciones de presión ni caudal. En las figuras 7 y 8 se puede observar el diferente comportamiento entre un ‘PM Flow Controller’ y un regulador de caudal de tubo capilar.
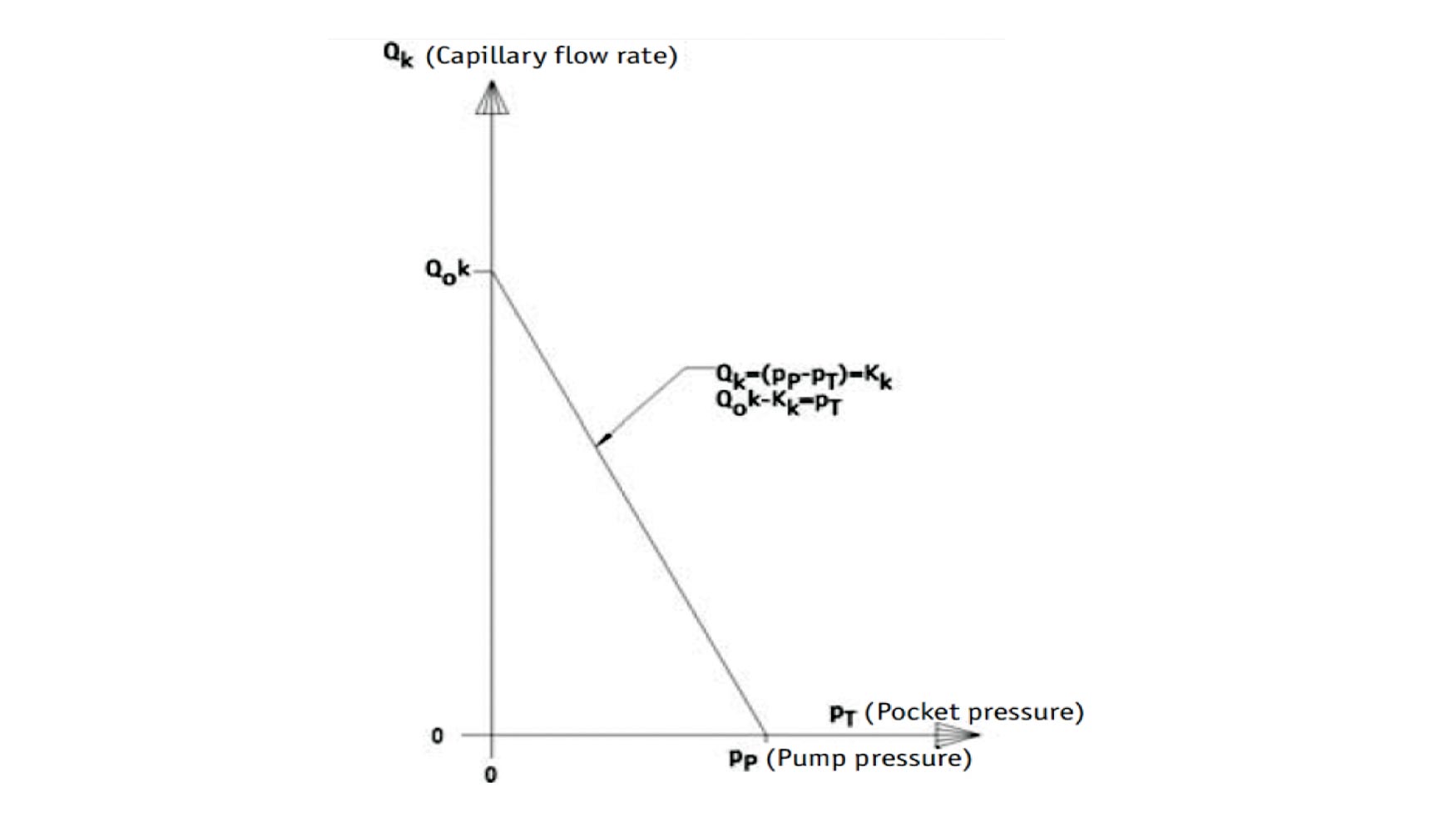
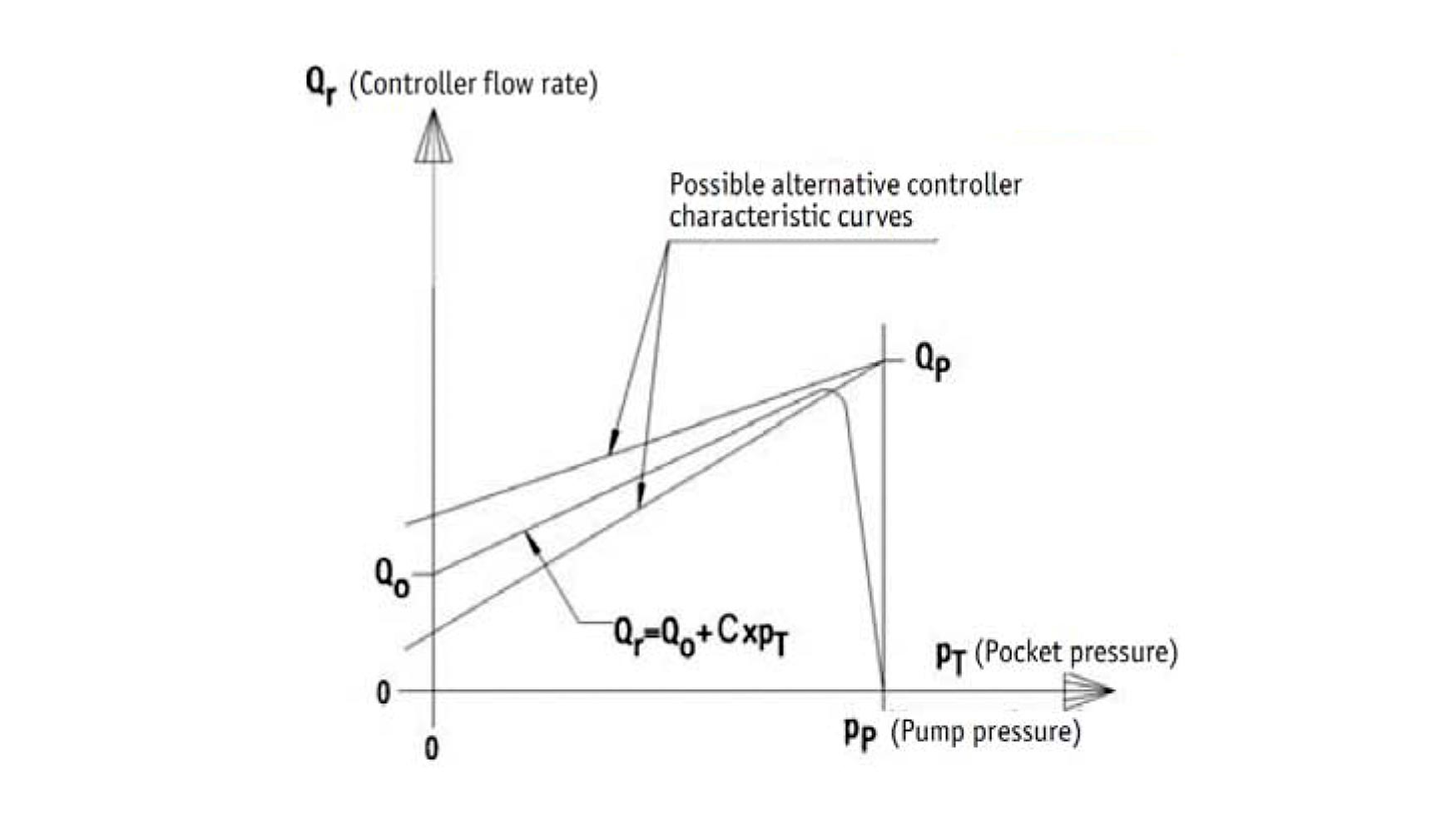
Las ventajas del sistema de Hyprostatik respecto a las soluciones de tubos capilares son:
- Mayor rigidez gracias al uso de controladores del flujo que reducen el rango de variación de la película de aceite. Aproximadamente 4 veces más rígido.
- Rapidez de ajuste del sistema: 4 horas frente a 1 semana
- Rapidez de respuesta del sistema
- Bajos costes de mantenimiento
- Menor caudal, lo que supone un ahorro de costes en el grupo hidráulico y el sistema de refrigeración
- No existe desgaste y se trabaja en condiciones de baja fricción, debido a que el sistema evita el contacto entre superficies (siempre que las piezas de la mesa se fabriquen con una precisión y rigidez adecuadas).
- Mayor amortiguamiento
- Son sencillos de ensamblar en la máquina debido a que no es necesario ajustar la longitud del tubo a la presión de la cavidad, como sucede en el caso de tubos capilares.
- Es posible realizar una puesta a punto del sistema midiendo la presión en las cavidades en diferentes situaciones
- No se puede bloquear, tal y como sucede en una válvula habitual, debido a que el control es realizado mediante un diafragma elástico
- Las características del flujo se mantienen constantes gracias a los canales de flujo anodizados y a la membrana de baja tensión
- Es económico en comparación a otras válvulas
- Tiene un sistema muy sencillo para la evacuación completa del aceite de la mesa: es suficiente con conectar la conexión de la bomba del PM-Flow controller con el depósito de aceite, una vez fijada la mesa.
En la tabla 1 se puede observar una comparativa entre tres tipos de reguladores de caudal: reguladores de caudal constante, reguladores de resistencia constante (tubos capilares) y ‘PM flow controllers’.
|
Regulation method |
Load carrying capacity at h-50 um (kN)
|
Maximum load carrying capacity (kN) |
Stiffness at h=50 um (kN/µm) |
Peak stiffness (kN/µm)
|
Working range of the throtling gap (um) |
|
Constant flow rate |
4,5 |
8,3 |
0,28 |
0,58 |
49,0 |
|
Constant resistance |
2,8 |
- |
0,11 |
0,17 |
85 |
|
PM regulator |
3,5 |
7,5 |
0,35 |
0,97 |
31 |
3. Metodología de diseño de la mesa rotatoria hidrostática de Sidepalsa
En el diseño de los cojinetes hidrostáticos existen muchos grados de libertad. El objetivo del diseño consiste en soportar las cargas estimadas y, además, proporcionar la rigidez necesaria con el mínimo coste, tanto de inversión como de operación, lo cual supone una minimización de la potencia de instalación de energía hidráulica, utilización de componentes sencillos y mínimas pérdidas por fricción. En el presente artículo se presenta una metodología de diseño que está orientada a concebir y desarrollar mesas rotatorias hidrostáticas que serán integradas en máquinas herramientas de muy elevada precisión, como medio para aunar en dichas máquinas precisión, productividad y calidad. La metodología consiste en un flujo de trabajo a llevar a cabo cuando se deba diseñar una mesa rotatoria hidrostática, en base a las especificaciones funcionales de partida. A partir de dichas especificaciones funcionales, se calculan automáticamente los parámetros principales de diseño, tales como, el número de celdas hidrostáticas, espesor de película del fluido, rigidez y amortiguamiento en cada cavidad, etc. Una vez determinados estos parámetros, se introducen como variables de entrada en un modelo MEF paramétrico de la mesa rotatoria hidrostática y, en base a unos objetivos previamente definidos de rigidez y amortiguamiento de la misma, se optimizan las dimensiones geométricas de los distintos componentes. De esta manera se consigue disminuir considerablemente el tiempo de diseño y optimización de las mesas rotatorias hidrostáticas.
3.1 Especificaciones funcionales
En la tabla 2 se muestran las especificaciones funcionales de la mesa hidrostática que son necesarias para su dimensionamiento y los valores para la aplicación concreta de Sidepalsa objeto de este proyecto.
|
Característica |
Valor |
|
Dimensiones de la mesa |
2.000 x 2.500 mm |
|
Velocidad de giro |
6 rpm |
|
Carga máxima centrada |
35.000 kg |
|
Diámetro máximo de la pieza a mecanizar |
2.500 mm |
|
Excentricidad máxima de la pieza a mecanizar |
300 mm |
|
Fuerza radial de mecanizado máxima |
30.000 N |
|
Fuerza axial de mecanizado máxima |
30.000 N |
Tabla 2. Especificaciones funcionales de la mesa rotatoria hidrostática Sidepalsa.
Por otra parte, en el cálculo hidrostático de la mesa es necesario considerar también como variables de entrada las fuerzas introducidas por el accionamiento de giro de las mismas. Con el fin de mantener un enfoque de diseño modular junto a las mesas rotatorias con cojinetes de rodadura de Sidepalsa, se decide mantener el mismo accionamiento en ambas, consistente en dos motor-reductores, cada uno con su piñón, que accionan entre ambos una corona. Tanto la corona como los piñones consisten en engranajes de dientes helicoidales. La corona arrastra en su giro a la parte móvil de la mesa rotatoria y a la pieza a mecanizar, situadas en su parte superior. A partir de las características de dicho accionamiento se han calculado las fuerzas radiales (Fdr) y axiales (Fda) introducidas en el sistema por el accionamiento. Estos valores se pueden observar en la tabla 3.
|
Característica |
Valor |
|
Fa (máxima fuerza axial de mecanizado) |
30.000 N |
|
Fr (máxima fuerza radial de mecanizado) |
30.000 N |
|
Ft (máxima fuerza tangencial de mecanizado) |
30.000 N |
|
Número de dientes piñón-corona |
23-232 |
|
Relación de reducción reductores i |
325 |
|
Ángulo entre los ejes de los dos motores |
18,81º |
|
Ángulo de presión de los engranajes |
20º |
|
Ángulo de hélice de los engranajes |
7º |
|
Fdt (fuerza tangencial del accionamiento en cada motor) |
28.138 N |
|
Fdr (fuerza radial del accionamiento en cada motor) |
4.448 N |
|
Fda (fuerza axial del accionamiento en cada motor) |
10.532 N |
Tabla 3. Fuerzas del accionamiento de la mesa hidrostática. Los valores iniciales, variables de entrada. Los 3 últimos, variables calculadas.
A continuación, se detallan el resto de parámetros geométricos del diseño inicial de la mesa hidrostática, en base al enfoque modular consistente en mantener en todo lo posible las mismas dimensiones que la mesa equivalente con cojinetes de rodadura.
|
Nomenclatura |
Dimensión |
Valor |
|
hb |
Distancia del centro del rodamiento radial a la superficie inferior del plato |
77,25 mm |
|
mt |
Peso del plato |
9.750 kg |
|
hf |
Máxima distancia de la fuerza de mecanizado a la superficie inferior del plato |
1.250 mm |
|
df |
Diámetro máximo de la pieza a mecanizar |
2.500 mm |
|
dxf |
Diámetro de la base de la mesa |
1.340 mm |
|
hd |
Distancia del eje del piñón de la transmisión a la superficie inferior del plato |
326 mm |
|
hmw |
Distancia máxima del centro de gravedad de la pieza a la superficie inferior del plato |
750 mm |
|
emw |
Valor máximo de la excentricidad de la pieza a mecanizar |
300 mm |
|
hmt |
Distancia del centro de gravedad del plato a su superficie interior |
125 mm |
A partir de estas especificaciones funcionales y restricciones geométricas se han calculado, mediante unas Hojas de Cálculo, la Fuerza Axial y el Momento de Vuelco que debe soportar la mesa hidrostática en diferentes casos de carga.
|
Fuerza axial |
Momento del vuelco |
|
477.500 N |
214.990 Nm |
|
417.500 N |
214.990 Nm |
|
177.500 N |
101.481 Nm |
|
117.500 N |
110.727 Nm |
|
92.500 N |
12.625 Nm |
3.2 Cálculo de los parámetros hidrostáticos
En los cálculos hidrostáticos existen más variables que ecuaciones. Debido a esto este cálculo es iterativo, por lo que es necesario utilizar un software que realice dichas iteraciones. Existen varios softwares comerciales especializados en realizar estos cálculos, por ejemplo ARMD 5.8 D2 de la empresa ARLA GmbH, RAPPID Software de la empresa RSR, y el software propio de la empresa suministradora de los ‘PM Flow controllers’, Hyprostatik. Dado que los cálculos de rigidez, amortiguamiento, caudal y temperatura del mismo, potencia de bombeo necesaria y pérdidas por fricción dependen del tipo de controlador de caudal utilizado, y dado que en este caso se ha decidido utilizar los ‘PM Flow controllers’, se ha decidido utilizar el software de Hyprostatik para el cálculo de los parámetros hidrostáticos.
Proceso iterativo de selección de parámetros hidrostáticos
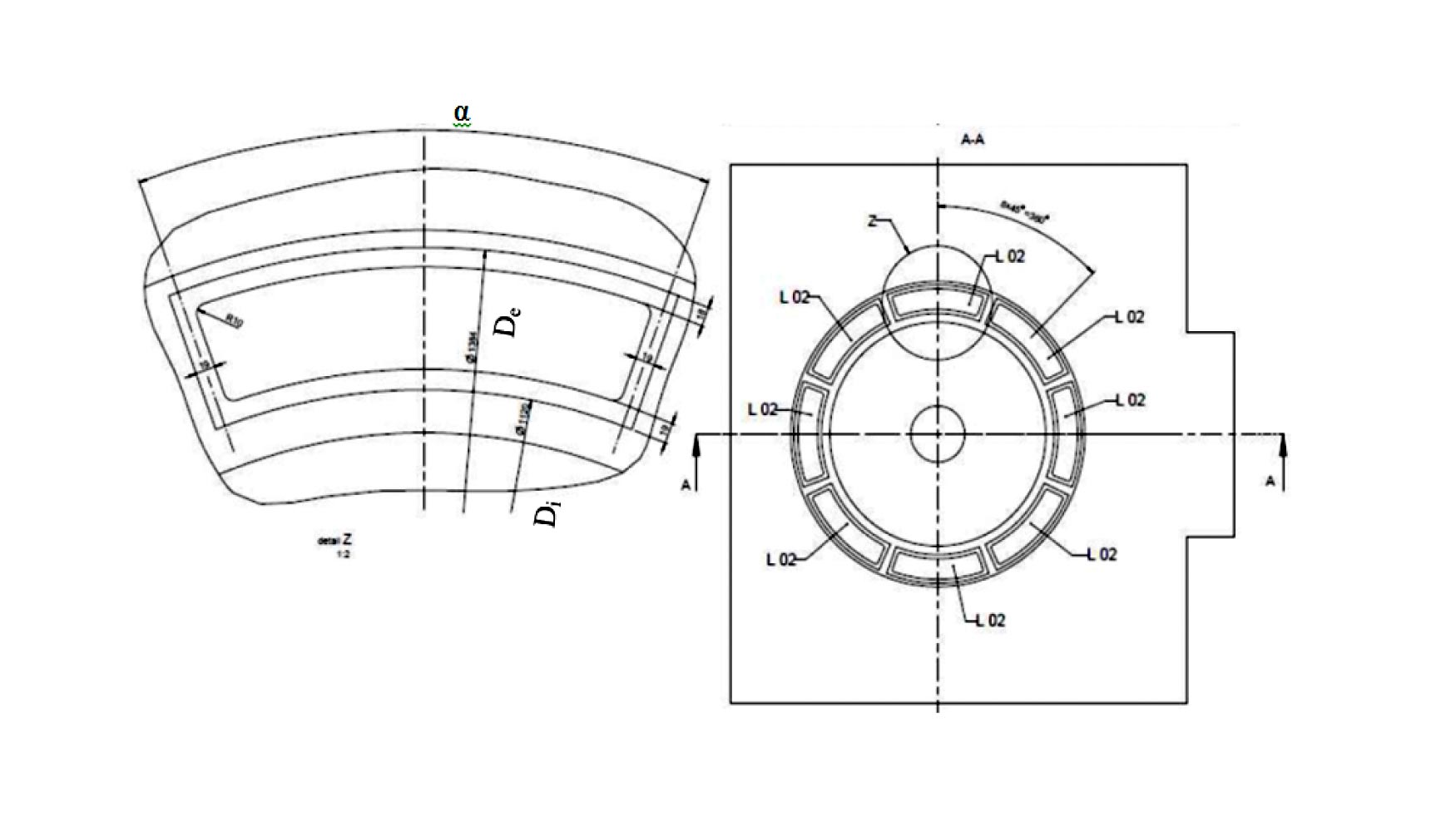
Debido a que, como se acaba de indicar, el cálculo es iterativo, hay que fijar algunas variables de antemano y a continuación realizar el cálculo. Posteriormente se van modificando estas variables de entrada hasta obtener el resultado deseado que cumpla tanto con las especificaciones funcionales como con las restricciones geométricas. Uno de los datos de entrada del software es el número de cavidades del sistema. En este caso, utilizando la experiencia previa, se ha optado por realizar el cálculo con 8 cavidades de elevación, 8 cavidades de retención (ver figura 9), todas ellas de una profundidad de 0.8 mm y unos valores prefijados iniciales de diámetros interior (Di) y exterior (De). A partir de dichas variables de entrada, el software proporciona los valores óptimos de las siguientes variables de salida:
- Aceite: tipo, temperatura de trabajo
- Presión de trabajo
- Geometría de cavidades: tamaño, localización y número
- Caudal del aceite.
- Coeficientes de película de las celdas de elevación (h01) y de retención (h02)
- Rigidez en cada celda hidrostática y Rigidez total
- Amortiguamiento en cada celda hidrostática y Amortiguamiento total.
Una vez obtenidos unos resultados para estos valores que cumplan con las especificaciones de Fuerzas y Momentos descritas en el punto 3.1, se han realizado los cambios oportunos en el diseño 3D de la mesa para comprobar si esa disposición de las celdas hidrostáticas es geométricamente posible.
Se ha seguido este proceso iterativo hasta conseguir una configuración de celdas hidrostáticas que cumplan tanto con las especificaciones de Fuerzas y Momentos como con las restricciones geométricas del diseño 3D de la mesa hidrostática. Una vez que se llega a una configuración que cumple con dichas especificaciones y restricciones geométricas, es necesario realizar un Análisis MEF del conjunto estructural de la mesa hidrostática, con el fin de comprobar si las piezas estructurales van a tener la rigidez suficiente para garantizar que los valores de los coeficientes de película h01y h02 se mantengan en un rango entre los valores calculados y un valor mínimo límite (h0l), necesario para el correcto funcionamiento del sistema hidrostático. En caso de que la deformación de dichas piezas estructurales bajo las distintas cargas, tanto las provenientes del accionamiento de la mesa como del sistema de células hidrostáticas, sea superior a los valores calculados de (h01-h0l) ó (h02-h0l), es necesario volver al paso inicial, cambiando parámetros del sistema hidrostático, hasta que se cumplan las especificaciones de Fuerzas y Momentos, las restricciones geométricas y los valores máximos de variación de los coeficientes de película. En la figura 10 se describe este flujo de trabajo.
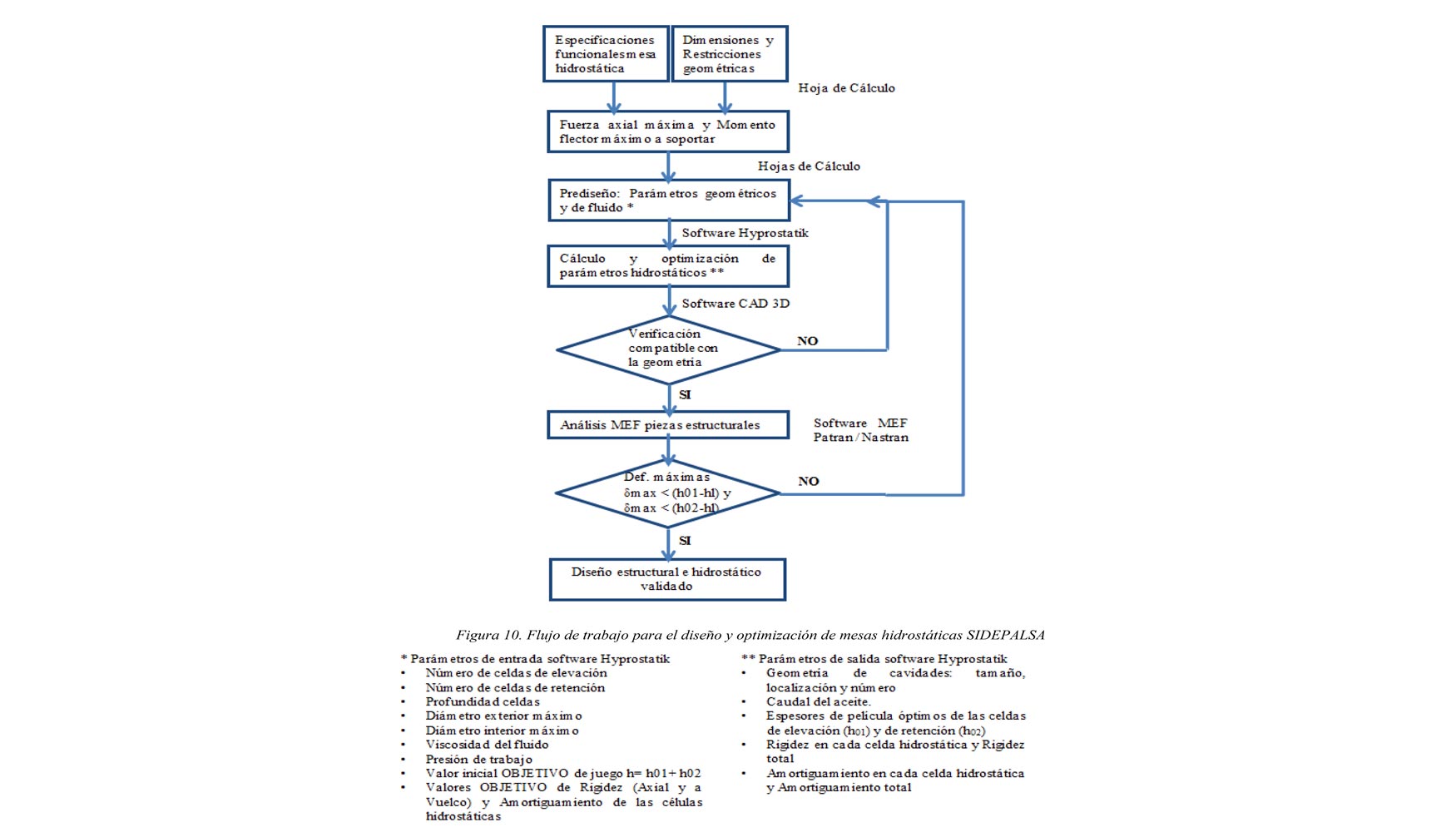
Al ser un cálculo iterativo, es necesario tener un objetivo. En este caso, este objetivo es obtener un espesor de película nominal (cada uno de los valores, h01 y h02) de al menos 0,028 mm (tanto en las cavidades de elevación como en las de retención), aceptando una variación máxima de 0,024 mm. Se han tomado estos valores por ser típicos en este tipo de aplicaciones. Una vez fijadas las variables de entrada, se ha utilizado el software para realizar las iteraciones necesarias hasta obtener los valores óptimos del cojinete axial hidrostático para las condiciones de carga indicadas en las especificaciones. Se ha realizado cálculos para distintos casos de carga, distintos valores de juego (h= h01+h02) y velocidad de giro. A continuación, se listan las variables de salida que proporciona el software para cada una de las celdas.
- Presión de la celda
- Rigidez axial y radial
- Amortiguamiento
- Relación potencia bomba/pérdidas por fricción
- Caudal del aceite a temperatura del aceite de 20 y 40 °C
- Temperatura del aceite a n= 5 rpm y 6 rpm
- Potencia de la bomba a temperatura del aceite de 20 y 40 °C
- Pérdidas por fricción a temperatura del aceite de 20 y 40 °C y revoluciones de giro óptimas y máximas.
- Pérdidas totales a temperatura del aceite de 20 y 40 °C y revoluciones de giro óptimas y máximas.
A continuación, se tiene en cuenta la influencia del momento de vuelco en el comportamiento del cojinete hidrostático, debido a la máxima excentricidad posible de la carga. Debido a este momento las presiones necesarias en las celdas para soportar los esfuerzos generados no son iguales. En la Tabla 6 se pueden observar resultados de presiones de trabajo y espesor de película en varias celdas distintas, bajo condiciones de carga que incluyen el máximo momento flector.
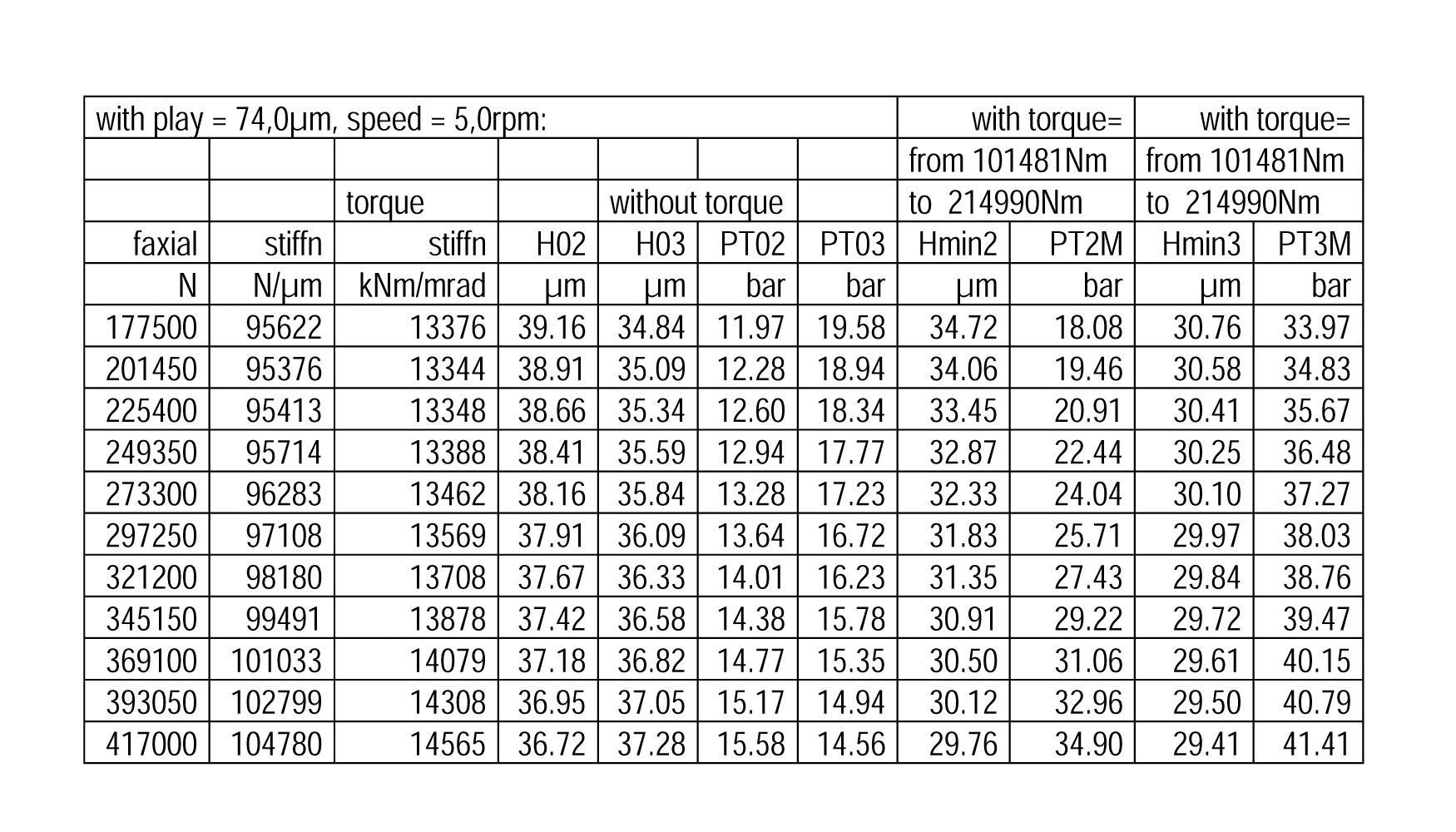
Posteriormente se ha realizado un análisis de sensibilidad para estudiar la influencia del juego h en la rigidez axial y al giro de las distintas celdas hidrostáticas, con el fin de optimizar el valor de dicho juego h.
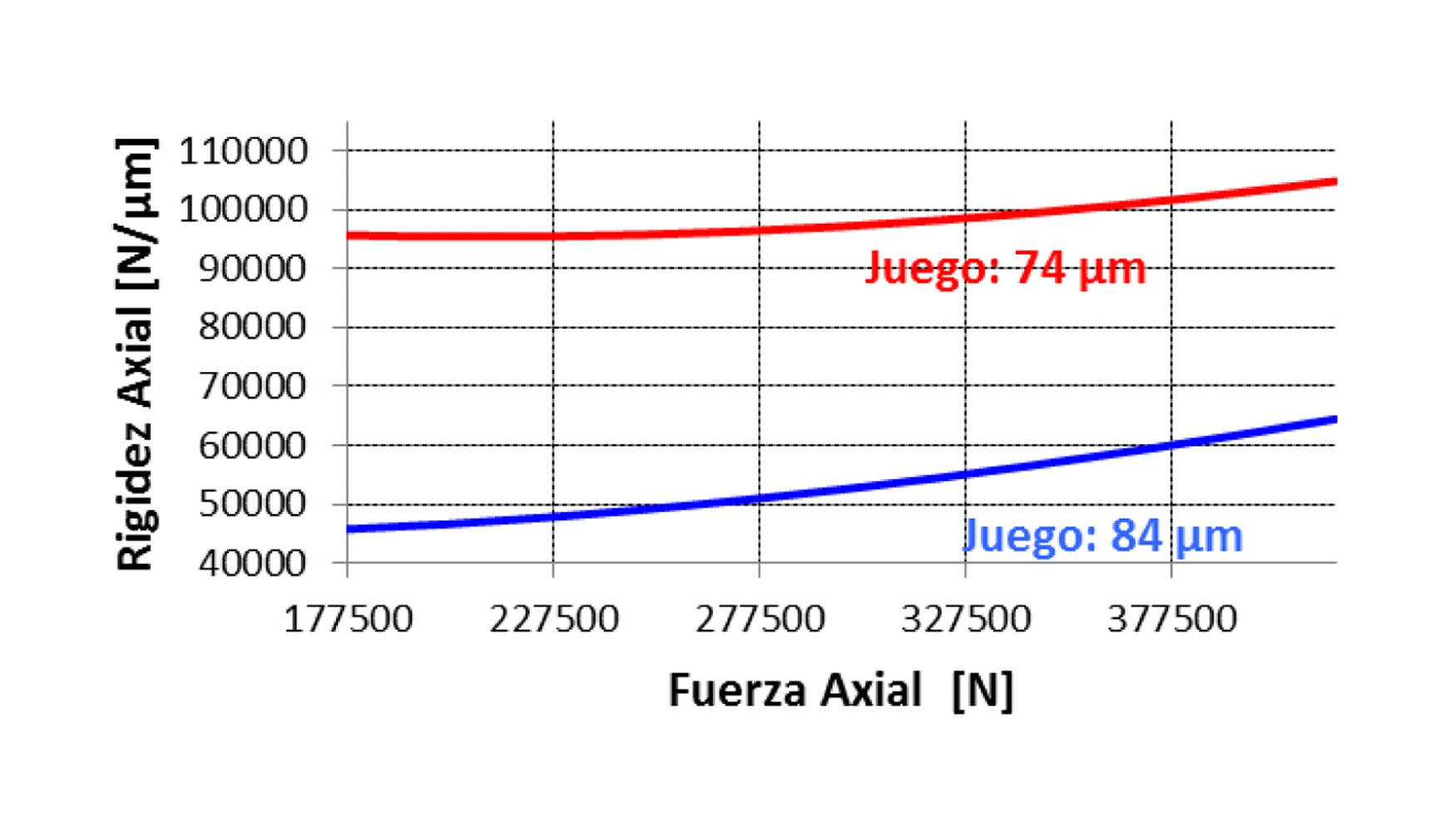
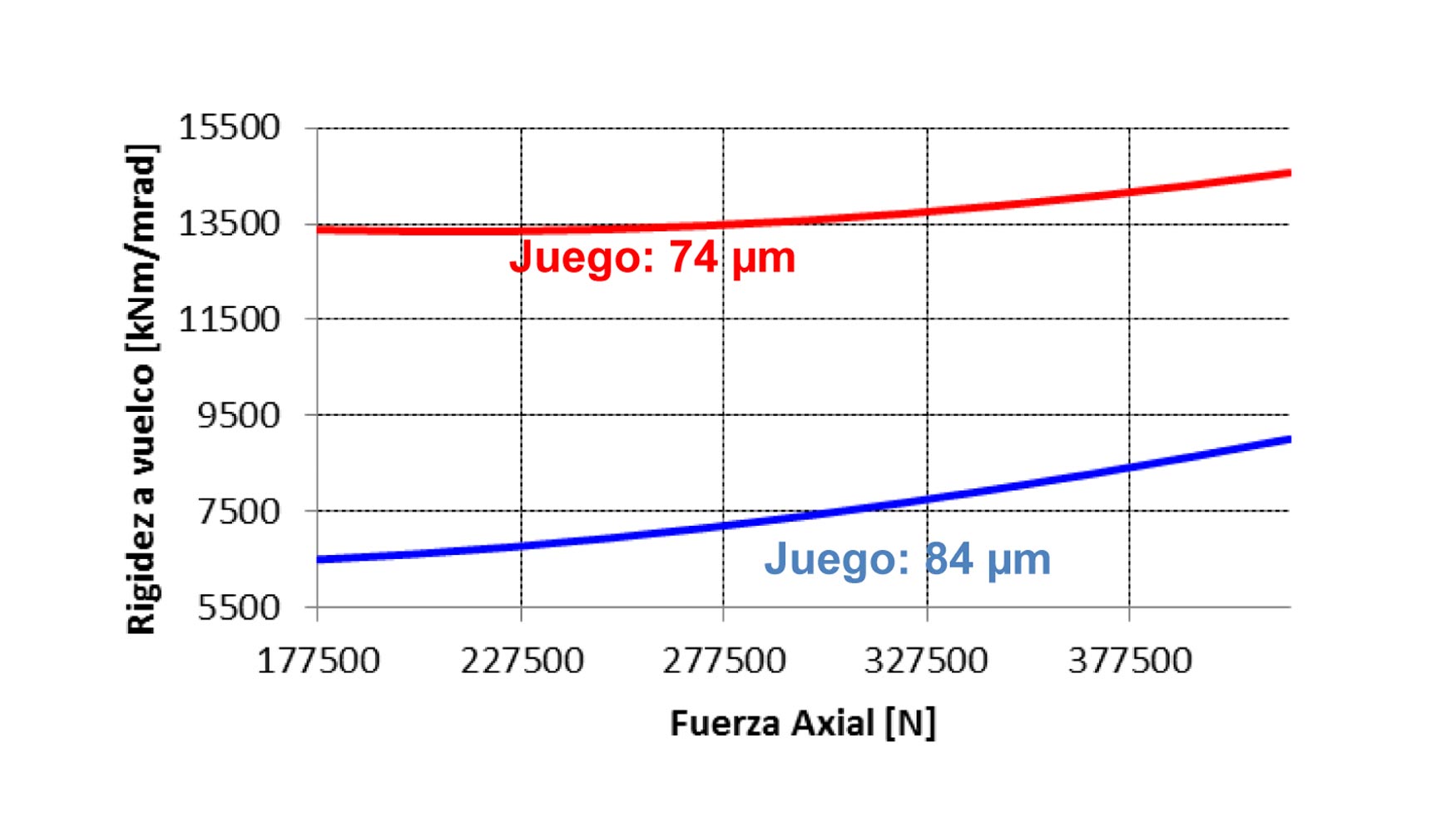
Se puede apreciar que tanto con las fuerzas axiales como con el momento de vuelco, cuanto más pequeño es el juego la rigidez es mayor, por lo que se deberá tender a trabajar con el menor juego posible. Otro factor a tener en cuenta es la velocidad de giro de la mesa. En la siguiente figura se puede observar la variación de la rigidez axial de las celdas hidrostáticas en función de la velocidad de giro, en el caso de un valor del juego h de 84 μm.
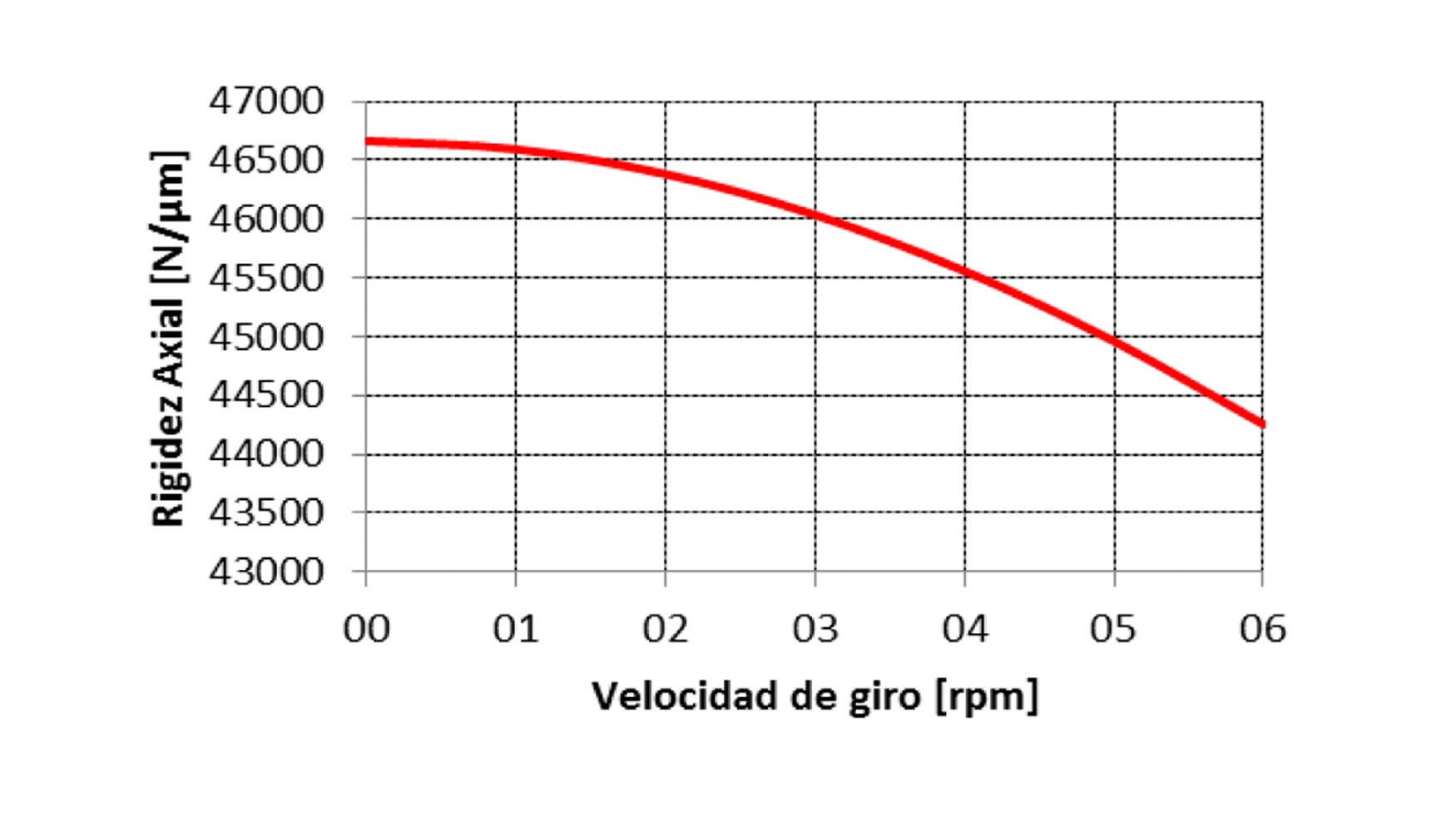
En la tabla 7 se presentan los valores máximos de las presiones y fuerzas en las cavidades de elevación y retención, y los valores máximos de fuerzas a la presión límite del PM Flow Controller (56,7 bar).
|
Cavidades |
Presiones/fuerzas máx. calculadas |
Fuezas límite a 56,7 bar |
|
Cavidad de elevación L02: 49.622 mm2 |
35,7 bar / 177 kN |
281 kN |
|
Cavidad de retención L03: 18.331 mm2 |
37,5 bar / 69 kN |
103 kN |
Amortiguamiento
El amortiguamiento en los cojinetes hidrostáticos es dependiente de la frecuencia de la excitación pero, en general, es del orden de 3 órdenes de magnitud superior al amortiguamiento de los cojinetes de rodadura. En este caso el mejor amortiguamiento se consigue con el aceite VG68 a 20-40°C. Las limitaciones de cara al amortiguamiento son la viscosidad del aceite, el espesor de película y la viscosidad. En la figura 14 se puede observar la variación del Amortiguamiento en función de la frecuencia.
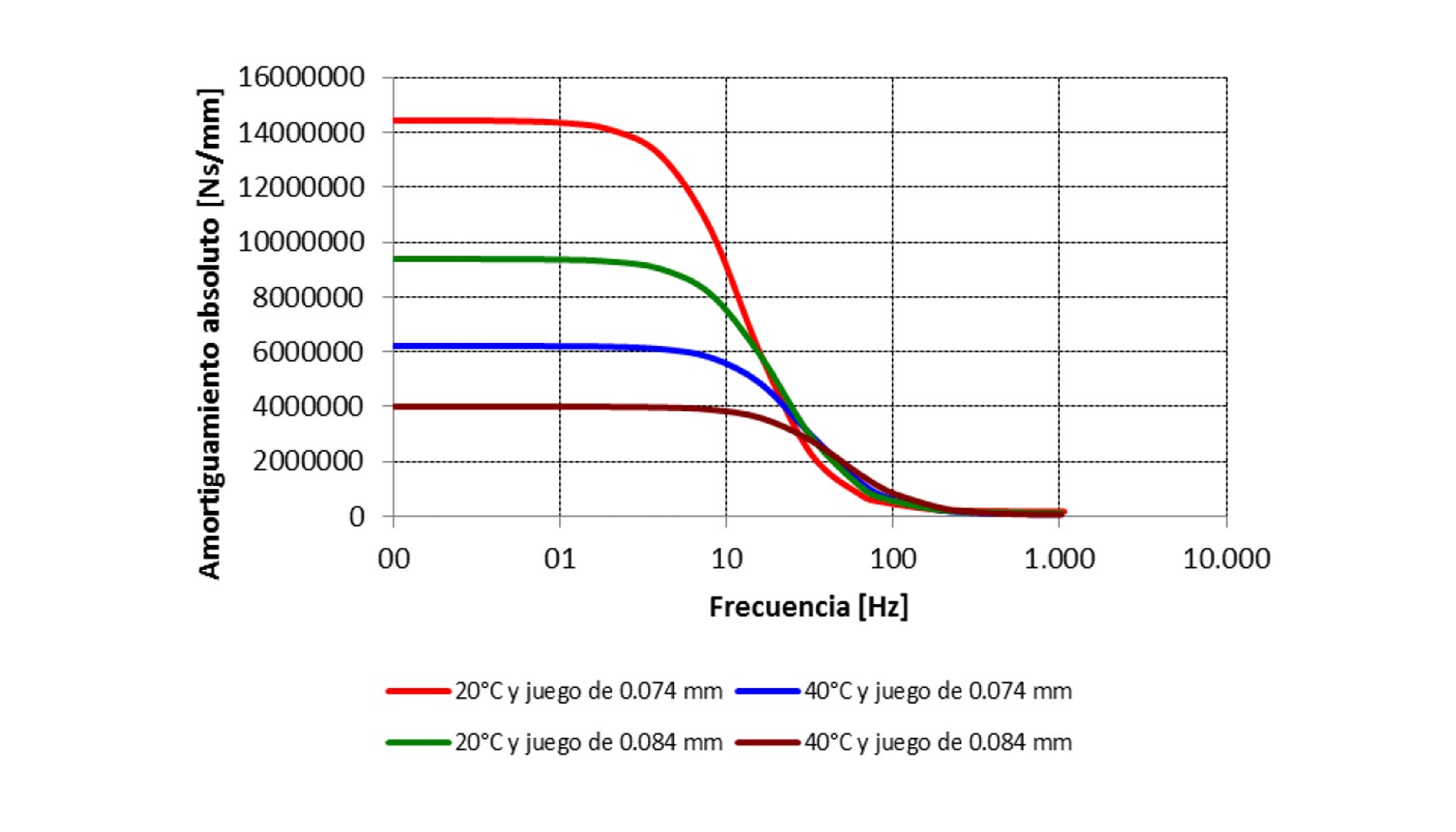
Caudal de aceite
El caudal necesario de aceite se ha calculado considerando una viscosidad del aceite de 68 mm²/s del aceite VG68, considerando una temperatura de 40 °C (temperatura máxima del aceite a la entrada del PM-flow controller). En la tabla 8 se presentan los resultados.
|
Celdas hidrostáticas |
Caudal aceite VG68 |
|
L02 cavidad elevación |
3,8 l/min |
|
L03 cavidad retención |
3,7 l/min |
|
Caudal total mesa a 40 ºC |
7,5 l/min |
|
+10% por la tolerancia de viscosida del aceite |
0,8 l/min |
|
+20% de reserva |
1,6 l/min |
|
Máximo caudal de aceite a 40 ºC |
9,9 l/min |
|
Mínimo caudal de aceite a 20 ºC |
2,3 l/min |
4. Diseño de la mesa rotatoria hidrostática de Sidepalsa
Siguiendo las recomendaciones del apartado anterior se ha procedido a diseñar la mesa rototraslante con cojinete hidrostático en el eje axial. Dicho cojinete hidrostático consta de 8 cavidades de elevación y 8 cavidades de retención.
Se ha decidido diseñar las cavidades postizas atornilladas a la base y a la corona. Se han diseñado las piezas de alrededor de las cavidades lo suficientemente rígidas para tener una deformación lo suficientemente pequeña de manera que interfiera lo menos posible en el comportamiento del cojinete hidrostático. Si la deformación de las piezas contiguas es demasiado elevada, el contacto se producirá antes de llegar a los 56,7 bares (presión límite en las cavidades). Se recuerda que a partir de 56,7 bares el ‘PM Flow controller’ empieza a trabajar fuera de rango y el espesor de película cae a 0. Para garantizar la rigidez de las piezas de alrededor de las cavidades, siguiendo el flujo de trabajo descrito en la figura 10, se ha realizado un análisis por elementos finitos.

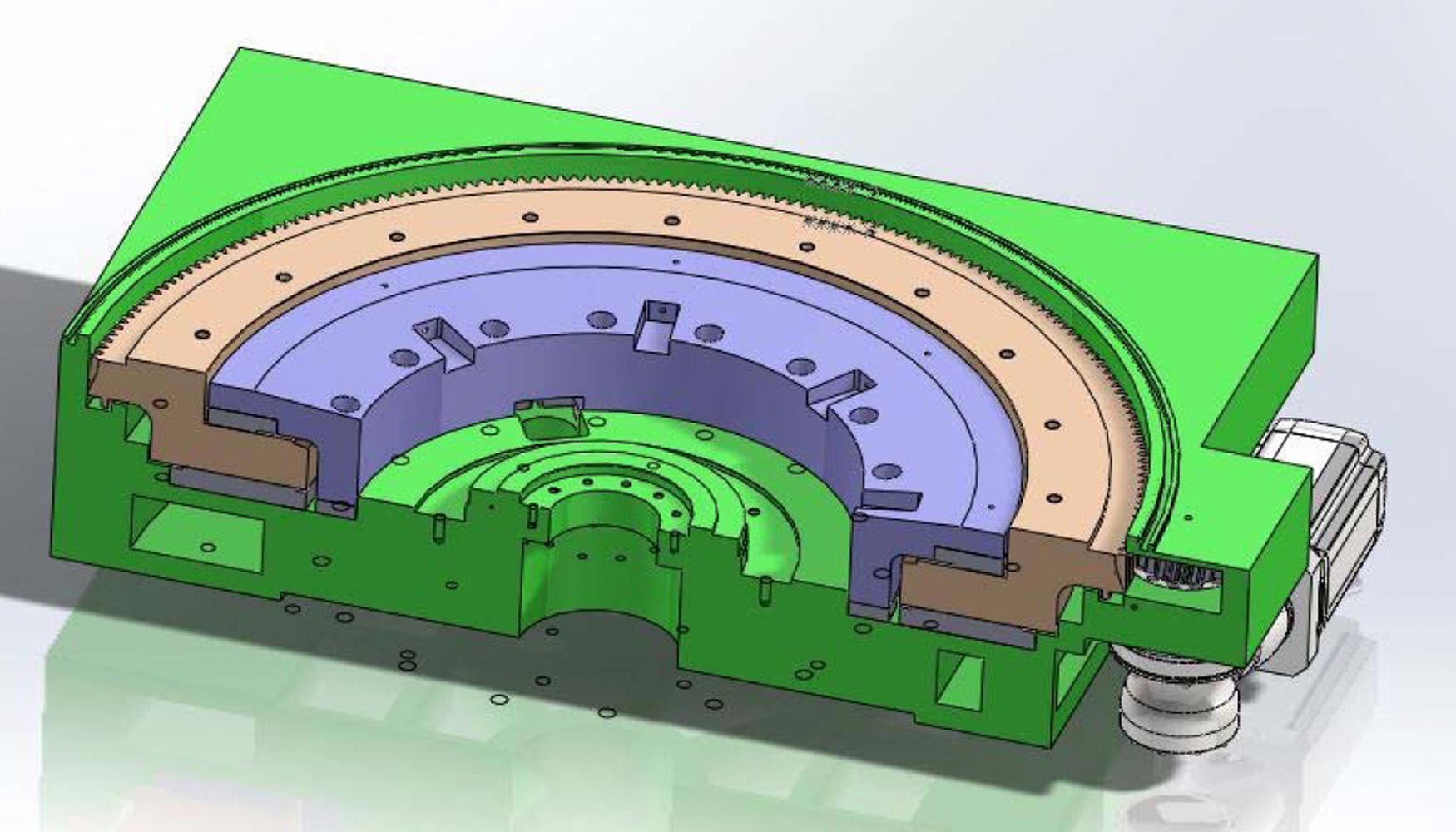
4.1 Cálculo y optimización MEF de piezas estructurales
Como se ha mencionado en el apartado 3, entre los resultados del software Hyprostatik se encuentran los valores de la rigidez y el amortiguamiento en cada celda hidrostática. En este caso concreto, se ha obtenido una rigidez equivalente máxima de 95.000 N/μm para juego=74 μm y 45.000 N/μm para juego =84 μm. En el software MEF se introducen los valores de rigidez de cada una de las celdas hidrostáticas, y además se aplica la presión del fluido en cada una de las superficies de contacto (ver figura 17). Esta presión hará que las piezas cercanas a las cavidades sufran deformación. El objetivo es cuantificar esos niveles de deformación y mantenerlos acotados.
Se han estudiado 4 combinaciones de casos de carga (ver figura 13) y se han analizado resultados de deformaciones y tensiones para esas tres combinaciones de casos:
- FTan: 76.000 N de fuerza tangencial + Presión lámina aceite + Peso Pieza.
- FRad: 150.000 N de fuerza radial + Presión lámina aceite + Peso Pieza.
- FVert: 300.000 N de fuerza vertical + Presión lámina aceite + Peso Pieza.
- FVert: 300.000 N de fuerza vertical + FRad: 150.000 N de fuerza radial + FTan: 76.000 N de fuerza tangencial + Presión lámina aceite + Peso Pieza.
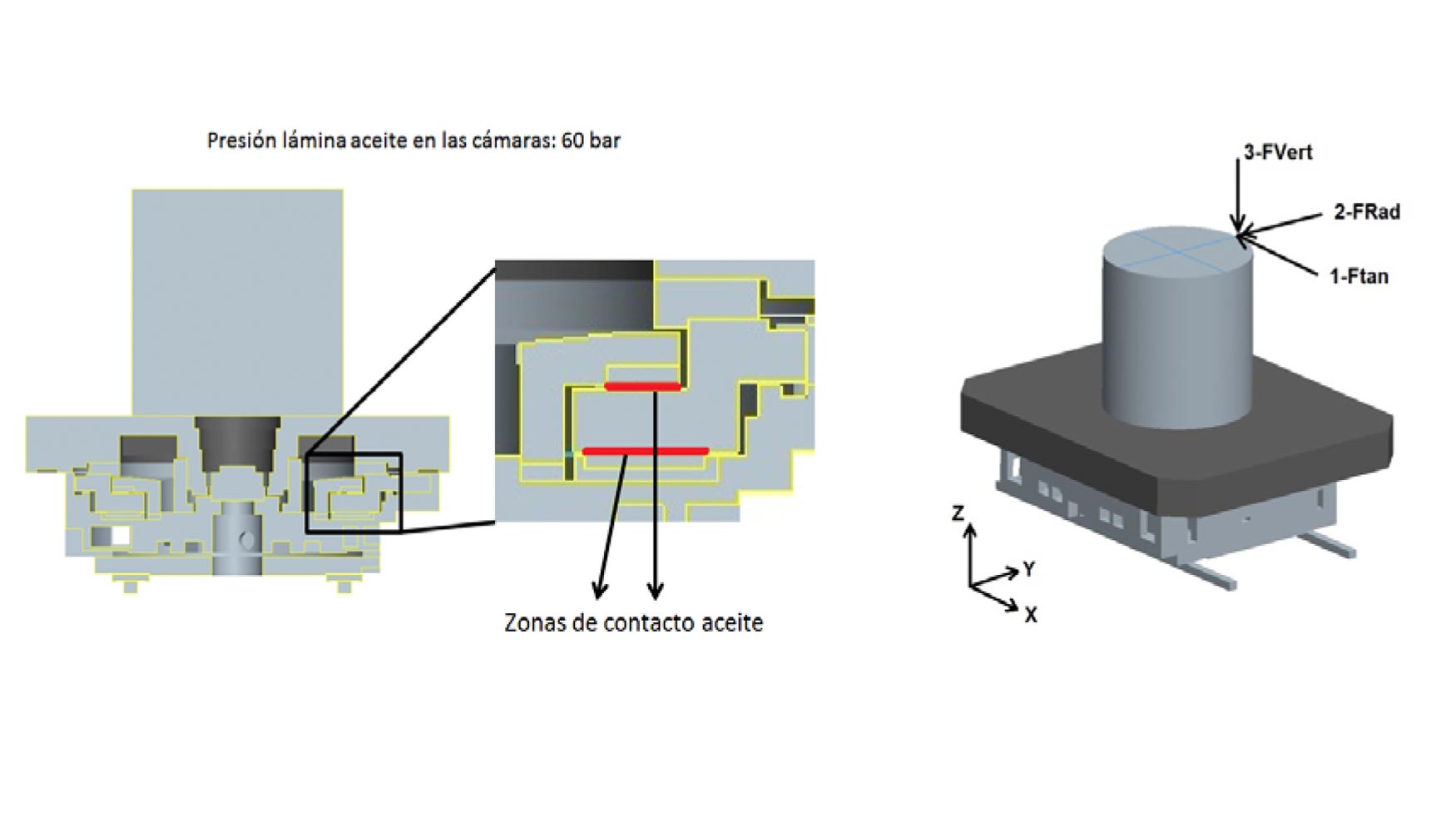
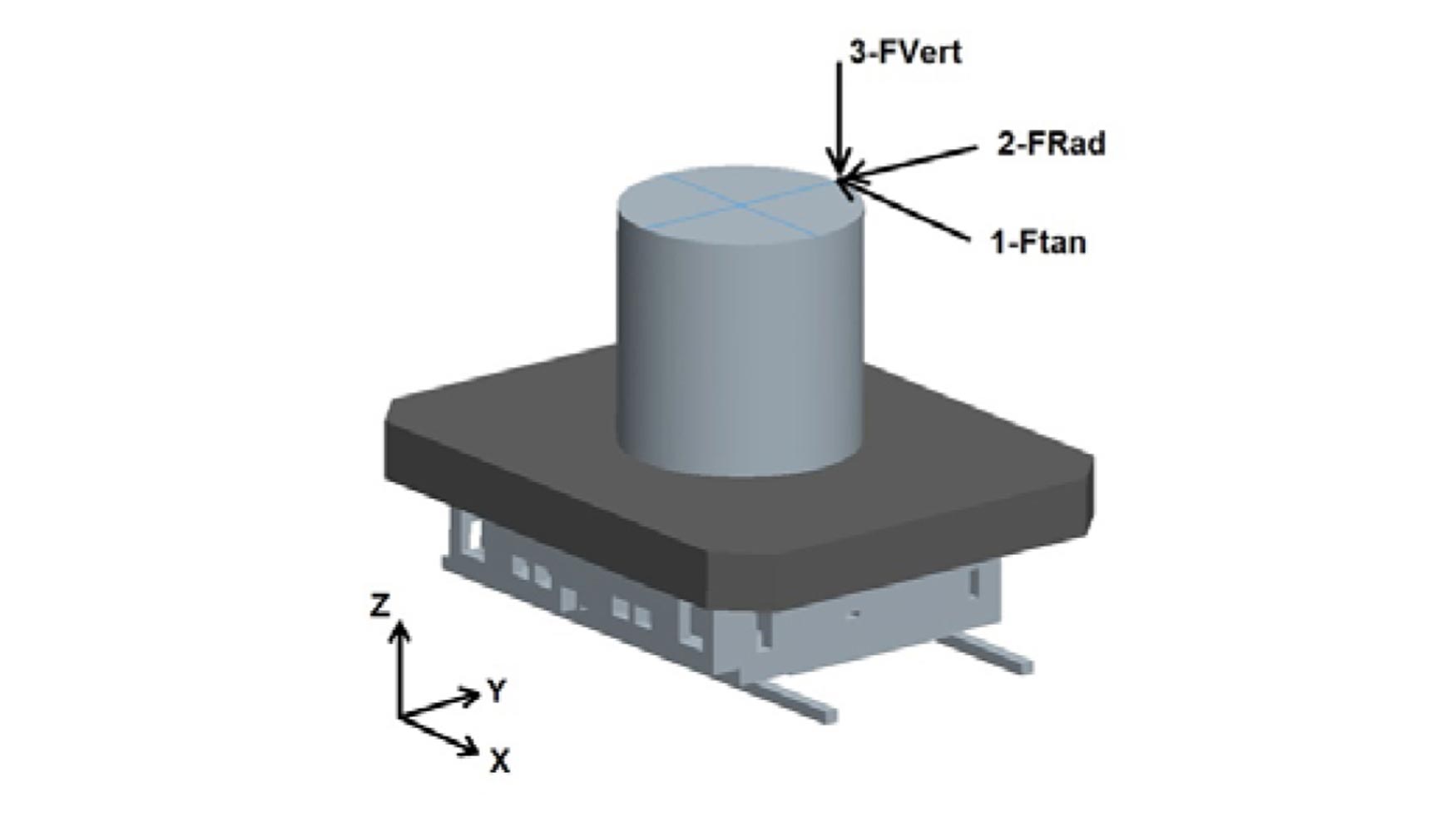
El objetivo que se ha definido es que la deformación relativa entre las piezas que conforman el apoyo hidráulico (zona de análisis) no supere las 24 μm. Se han realizado simulaciones MEF variando distintas dimensiones (cumpliendo con las restricciones geométricas). En la figura 19 se pueden observar los resultados del diseño optimizado para el Caso 4 de carga, que es el más exigente.
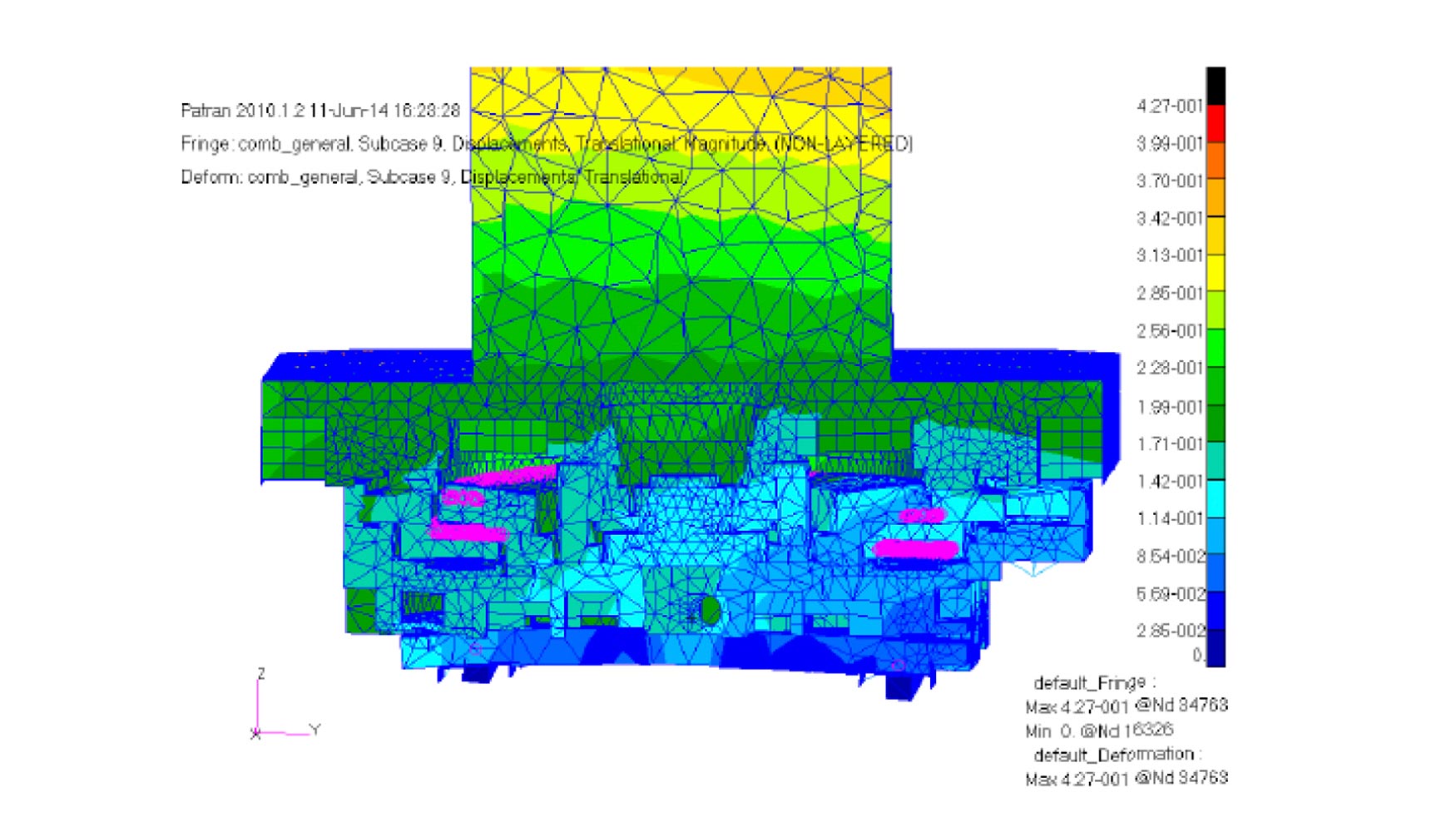
Una conclusión importante que se extrae del estudio MEF realizado es que los valores de deformación varían sustancialmente cuando disminuye la rigidez de la película de aceite (originada por la variación de espesor del hueco). De aquí se concluye que en la fase de montaje es crítico calibrar la mesa hidrostática con un juego de 74 micras.
4.2 Diseño en detalle de la mesa rotatoria hidrostática
Una vez realizado el análisis MEF, se ha procedido a diseñar en detalle la mesa rotatoria hidrostática de Sidepalsa. Se ha realizado el diseño 3D de detalle de todos los componentes que se han modificado como consecuencia de incluir el cojinete hidrostático. El diseño ha incluido el diseño de las cavidades, la localización de los PM-Flow controllers, los tubos y orificios desde la base a los PM-Flow controllers y desde los PM-Flow controllers hasta las cavidades y el sistema de retorno del aceite. Se ha realizado un diseño compacto de la mesa en el que todo el sistema hidráulico se integra en la propia mesa. La base de la mesa es el depósito de aceite y tiene una capacidad máxima de 100 litros. De la base se bombea el aceite a los 4 reguladores de flujo (PM flow controllers), los cuales alimentan, a su vez, a las 16 cavidades de la mesa. Cada unidad de regulador de flujo es capaz de alimentar a 4 cavidades.
El aceite caliente que desborda de las cavidades cae de nuevo a la base de la mesa. Para garantizar que la temperatura del aceite que llega a los reguladores de flujo es siempre inferior a 40 °C, se ha colocado un sistema de refrigeración por agua que coge el aceite de la zona que alimenta a la bomba principal, lo enfría y lo devuelve al depósito. En la siguiente figura se muestra una imagen con los diferentes componentes del sistema hidráulico
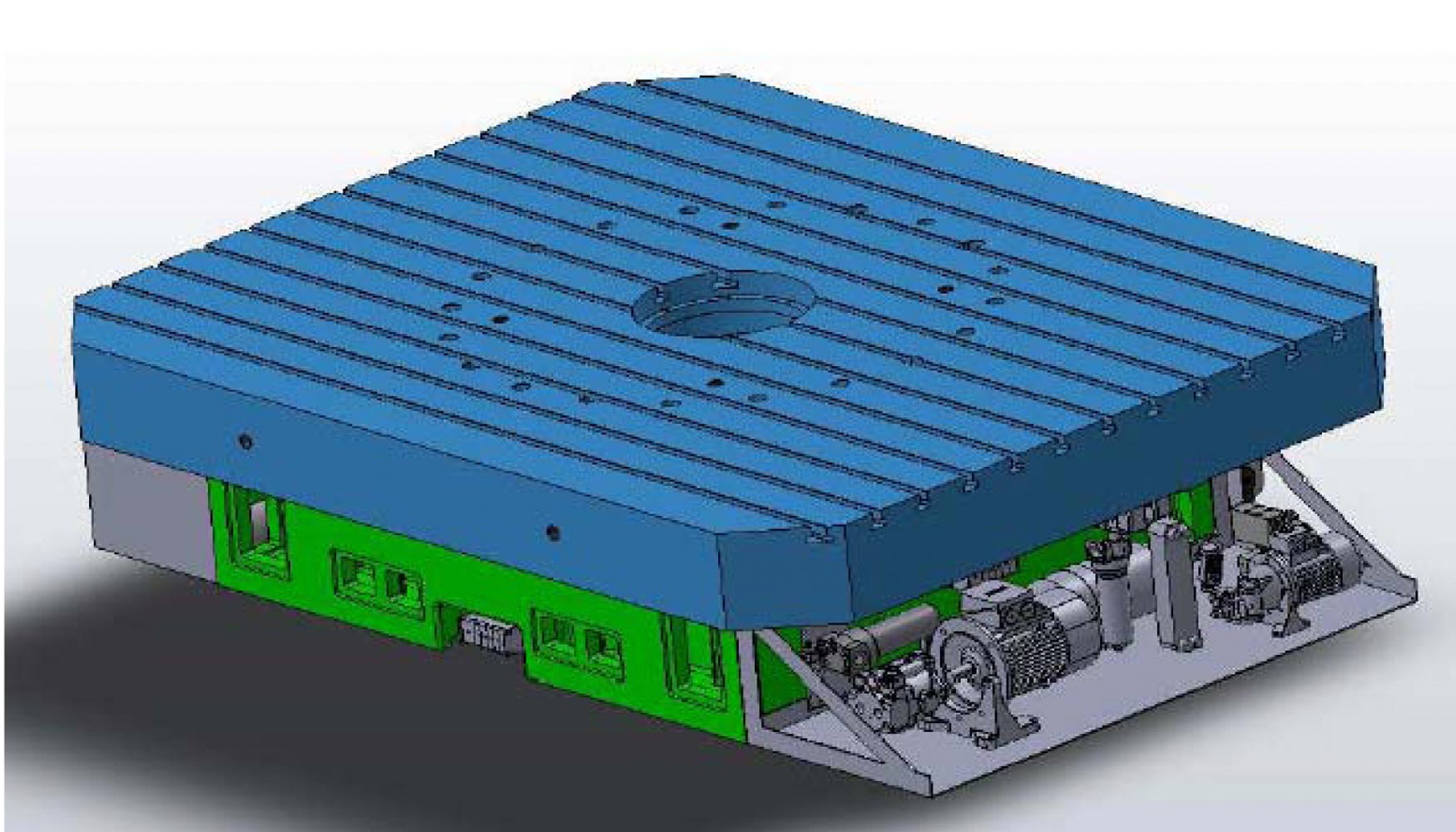
Para garantizar el correcto funcionamiento de la mesa es necesario que tanto el aceite como todos los conductos por los que pase y propio grupo hidráulico estén perfectamente limpios y libres de rebabas. En caso de que entre suciedad mayor a 0,02 mm, la suciedad puede quedarse en las cavidades; en este caso, las cavidades resultarían dañadas. Por lo tanto, es imprescindible trabajar con un aceite lo más limpio posible. Para ello todos los tubos y orificios entre el grupo hidráulico y las cavidades deben estar libres de rebabas y muy limpios antes de que se monte el ‘PM flow controller’. Por otro lado, el aceite debe ser filtrado a 6 μm a la entrada del ‘PM flow controller’. El aceite sale de las cavidades continuamente, por lo que debe retornar a tanque a través de canales y tubos sin que se mezcle con suciedad, viruta u otro líquido. Para ello, se ha diseñado un sistema de retorno que esté convenientemente sellado para que no pueda entrar en ella ninguna polución.
5. Conclusiones
En resumen de la metodología presentada se desprende que la utilización de reguladores de caudal ‘PM Flow Controllers’ reduce en un 80% el tiempo de puesta a punto de las mesas hidrostáticas, al mismo tiempo que permite multiplicar por 4 la rigidez de las celdas hidrostáticas en comparación a los reguladores de caudal de tubo capilar, y mantener constante el espesor de película, y por ende la rigidez, para distintas condiciones de carga, lo que conlleva un incremento considerable de la precisión y calidad del mecanizado.
Agradecimientos
El desarrollo de la mesa rotatoria hidrostática de Sidepalsa ha sido realizado durante el proyecto Mhidros ‘Desarrollo de una gama innovadora de mesas rototraslantes modulares, eco-eficientes y de ajustable capacidad de carga’. El proyecto ha sido cofinanciado por el Gobierno Vasco, bajo el programa I+D+i de Apoyo al Sector Empresarial en Euskadi - Proyectos de Desarrollo de Nuevos Productos – Gaitek.
Referencias
[1] Sharma, S.C., Jain, S.C. & Bharuka, D.K. (2002), Influence of Recess Shape on the Performance of a Capillary Compensated Circular Thrust Pad Hydrostatic Bearing. Tribology International 35, pp. 347-356.
[2] Shie, J.-S. & Shih, M.-CH. (2010), A Study on Optimization Design of a Hydrostatic Bearing. Proceedings of international forum on systems and mechatronics, pp. 1-6.
[3] HeirinchsonN., Fuerst A. and SantosI. F. The influence of injection pockets on the performance of tilting-pad thrust bearings. Journal of Tribology ASME, 2007, 129(4):895-903.
[4] Novikov E. A., Shitikov I. A. and Maksimov V. A. Characteristics of hydrostatic thrust bearing [J]. Khimicheskoe Neftegazovoe Mashinostroenie, 2004, 12(4): 23-26.
[5] Ma Wen-qi, Jiang Ji-hai and Zhao Ke-ding. Resea- rch on temperature rise of hydrostatic thrust bearing under variable viscosity [J]. China Mechanical Engi- neering, 2001,12(8): 953-955(in Chinese).
[6] Jiang Ji-hai, Ma Wen-qi and Zhao Ke-ding. Chara- cteristic analysis of annular hydrostatic bearing based on variable viscosity [J]. Journal of Harbin Institute of Technology, 2000, 32(4): 19-25(in Chinese).
[7] Chen G. H., Kang Y. and Chang Y. P. et al. In- fluences of recess geometry and restrictor dimension on flow patterns and pressure distribution of hydrostatic bearings [C]. American Society of Mechanical Engi- neers, Proceedings. Ann Arbor, USA, 2007, 2: 1045-1053.
[8] Shao Jun-peng, Zhang Yan-qin. Numerical simula- tion analysis of sector and circular oil recess tempera- ture field of heavy hydrostatic [J]. Journal of Hydro- dynamics, Ser. A, 2009, 24(1): 119-123(in Chinese).
[9] Shao Jun-peng, Zhang Yan-qin and LI Peng-cheng. Static flow simulation of hydrostatic bearing ellipse and sector curve based on fluent [J]. Lubrication Enginee- ring, 2007, 32(1):93-95(in Chinese).
[10] Shao Jun-peng, Dai Chun-xi and Zhang Yan-qin et al. The effect of oil cavity depth on temperature field in heavy hydrostatic thrust bearing [J]. Journal of Hydro- dynamics, 2011, 123(5): 676-680.
[11] Zhang Yan-qin, Shao Jun-peng and NI Shi-qian. Numerical simulation of temperature field in large size hydrostatic bearing [J]. China Mechanical Engineering, 2008, 19(5): 563-565(in Chinese).
[12] http://24005-hyprostatik.imosnet.de/fileadmin/inhalte/pdfs/hydrostatic_guides.pdf


