La relación entre el consumo específico y la fragmentación: el abanico fragmentación-energía

Este artículo investiga la fragmentación producida en una cantera de áridos siguiendo el concepto del abanico de fragmentación-energía. Para ello se han monitorizado seis voladuras consecutivas situadas en la misma zona de la cantera. La roca está estructurada en bloques, haciendo que el nivel del agua y el uso de explosivos sea variable entre barrenos de la misma voladura y entre voladuras. El consumo específico por encima del piso se encontraba entre 0,28 y 0,44 kg/m³. La fragmentación en la planta se midió usando un sistema digital de imágenes online y tres básculas. El material más grueso que no se ha podido tratar en la planta después de las voladuras se encuentra en el rango del 3 al 9,3% del total.

Los datos producidos por el sistema de imágenes se han empleado para reconstruir la curva granulométrica en el rango de los gruesos (fragmentos mayores de 120 mm), mientras que la fracción entre 120 y 25 mm se ha obtenido con los datos de las básculas. Los tamaños con percentiles entre 10 y 90% de cada voladura se describen a través de funciones potenciales basadas en el consumo específico por encima del piso; los coeficientes de los modelos resultan estadísticamente significativos.

Con estos datos, y teniendo como base los principios del modelo de abanico de fragmentación-energía y las propiedades de la distribución de Swebrec, la fragmentación se puede expresar en función del consumo específico a través de cinco parámetros: las coordenadas del punto focal del abanico y tres parámetros empleados como exponenciales versus el porcentaje de paso. El modelo desarrollado muestra una gran capacidad para describir la fragmentación.

La instalación de un sistema de análisis de imágenes antes de llevar el material a la trituradora primaria nos permite cuantificar la influencia de las características de la voladura en la fragmentación. En particular, la influencia del factor de carga o consumo específico en el tamaño de los fragmentos (especialmente en el tamaño medio) ha sido estudiada desde principios de 1970 por investigadores soviéticos (Koshelev et al., 1971, Kuznetsov, 1973). Estos trabajos fueron ampliados en años posteriores por Cunningham (1983, 1987, 2005) dando lugar a su modelo Kuz-Ram, y otros modelos posteriores derivados de él, como el modelo Crush-zone (Kanchibotla et al., 1999, Thornton et al., 2001).

Los modelos Kuz-Ram y Crush-zone presuponen siempre la función de distribución de Rosin-Rammler (Rosin and Rammler, 1933) y, por ende, su objetivo es predecir o calcular los parámetros de dicha distribución (por ejemplo, el tamaño de la mediana y un índice de uniformidad) en función de las características de la roca y de la voladura. El funcionamiento de estos modelos es relativamente pobre cuando se comparan con fragmentaciones medidas mediante el cribado de las voladuras (Sanchidrián and Ouchterlony, 2017). Uno de los motivos por lo que no termina de funcionar bien, es que la función de Rosin-Ramler no es un buen descriptor de la curva granulométrica de una voladura o está definida en un rango limitado de pase (Ouchterlony 2005, 2009, Sanchidrián et al. 2012a, 2012b, 2014, Sanchidrián 2015).

Una alternativa válida es centrarse en la determinación de ecuaciones de predicción de fragmentación independientes de la distribución para el tamaño de los percentiles como función del consumo específico, ver los trabajos realizados por Chung y Katsabanis (2000), Olsson et al. (2003), y Ouchterlony et al. (2010, 2015), entre otros. Ouchterlony et al. (2017) ha demostrado recientemente, a través del análisis de numerosos datos, que el índice de uniformidad de la función de Rosin-Rammler, tiene que ser variable en los diferentes percentiles para representar la fragmentación según los diferentes niveles de energía – o en términos de voladuras, factores de carga. Este modelo se conoce como el abanico de fragmentación-energía (fragmentation-energy fan) puesto que se deriva del dibujo de numerosos percentiles en función del consumo específico, resultando en una serie de líneas rectas en un espacio log-log que convergen en un punto focal común.

Este nuevo concepto basado en modelos de distribución libres proporciona un tamaño de fragmento para varios porcentajes de pase en función de las características del macizo rocoso y de la voladura en sí misma (Ouchterlony et al., 2017, Sanchidrián and Ouchterlony, 2017), sin la necesidad de recurrir a una función de distribución determinada. Los principios del modelo de abanico de fragmentación-energía son los seguidos en este trabajo para describir la fragmentación por voladura en una cantera de áridos. Este artículo es una versión condensada de Segarra et al. (2018), donde los datos y los análisis realizados se describen de manera detallada.

El trabajo experimental se ha llevado a cabo en la cantera El Aljibe. Dicha cantera, productora de milonita, está situada cerca de Almonacid de Toledo. La milonita producida se emplea en balasto para vías de trenes de alta velocidad y convencionales. La composición mineral de la milonita es similar a una granodiorita o a un granito tonalítico. Tiene una densidad de 2710 kg/m³ y una resistencia a compresión simple (media) igual a 131 MPa. El macizo rocoso donde se encuentra se puede describir como de fracturación por bloques.

Generalmente, sólo se carga una voladura durante un turno de trabajo. El tamaño máximo de los bloques es de unos 2 m. Los bolos o bloques de más de 900 mm, tamaño máximo de la trituradora primaria, se fragmentan in situ con el uso de un martillo hidráulico y posteriormente, se mezclan con el resto del material (de menos de 900 mm) de la voladura y se transportan a la planta. El número de fragmentos se puede dividir en dos categorías: pequeños, que pueden ser transportados, pero posiblemente bloqueen la entrada de la trituradora, con un tamaño medio mayor de 1 m; y grandes, que no pueden ser ni cargados, con un tamaño medio entre 1,5 y 2 m. Para el cálculo, hemos tenido en cuenta un tamaño medio de 1,1 y 1,7 respectivamente.

En la planta, un alimentador de rejilla con un límite de paso de 120 mm (apertura equivalente a una malla cuadrada) se emplea para separar la alimentación de la trituradora primaria (Departamento Técnico de Benito Arnó e Hijos, 2005).

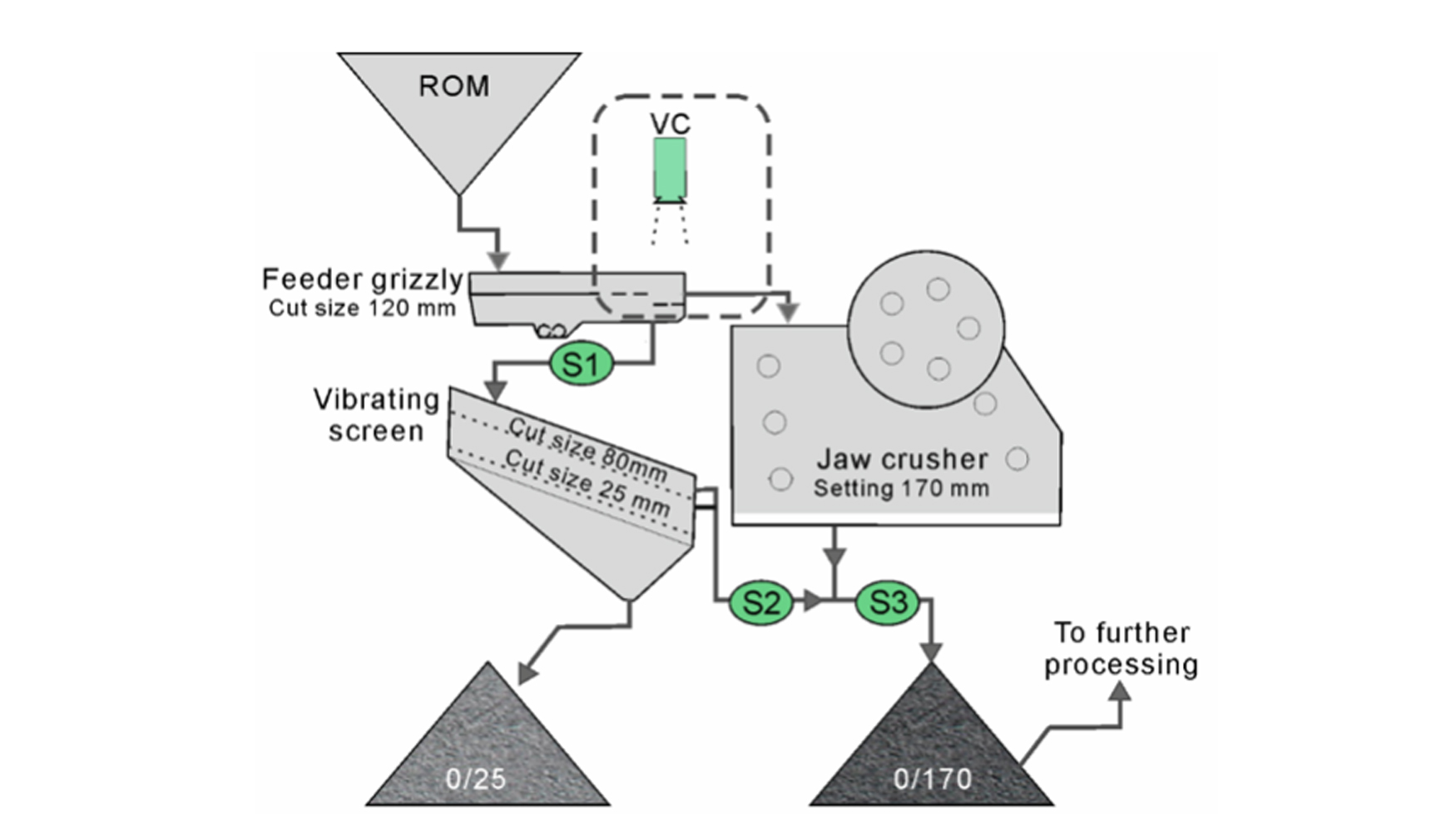
La derivación de la trituradora (<120 mm) separa con una criba vibradora a dos tamaños. Desde arriba hacia abajo, tiene aperturas circulares y cuadradas con límites de paso de 80 y 25 mm, respectivamente. La fracción más pequeña (<25 mm) se almacena en una pila, mientras que las fracciones más gruesas (120/80 mm y 80/25 mm) se añaden al flujo externo de la trituradora (<170 mm) y se almacenan en otra pila para un procesado adicional. La Figura 1 muestra un esquema de estas operaciones. También se muestran las localizaciones de los sistemas de medida de la fragmentación, llamados: básculas (identificadas como S1, S2 y S3) y la cámara de vídeo (identificada como VC).

Las voladuras estaban situadas una detrás de otra en el mismo banco de la parte noroeste de la corta. Esto se traduce en que la orientación de las fracturas naturales del macizo rocoso con respecto a la cara libre era similar en todas ellas. Cada voladura consistió en tres filas de barrenos perforados con un patrón al tresbolillo. Los barrenos eran de 89 mm de diámetro con una inclinación desde la vertical de 9º. La Tabla 1 muestra otras características de la voladura.

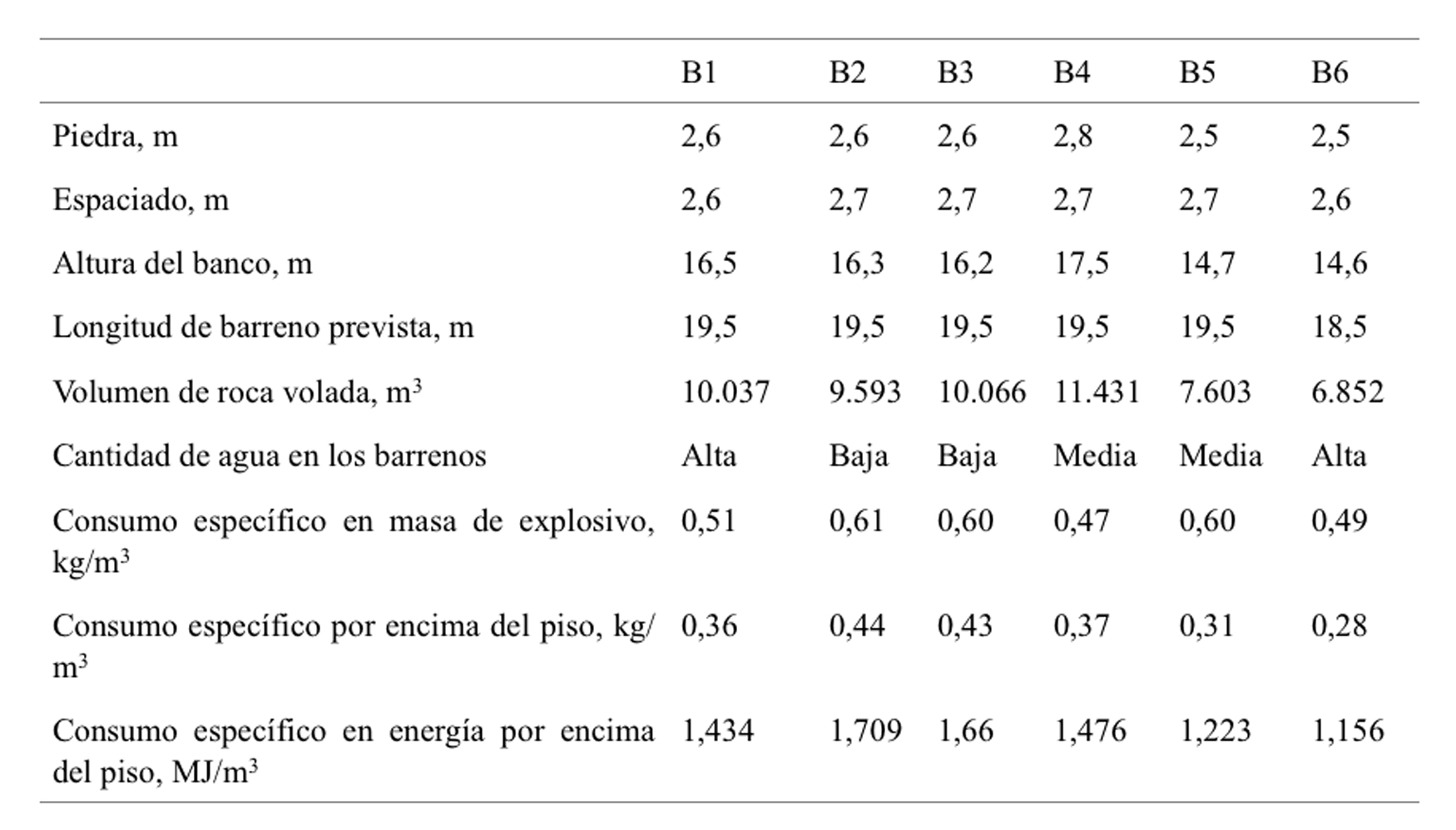
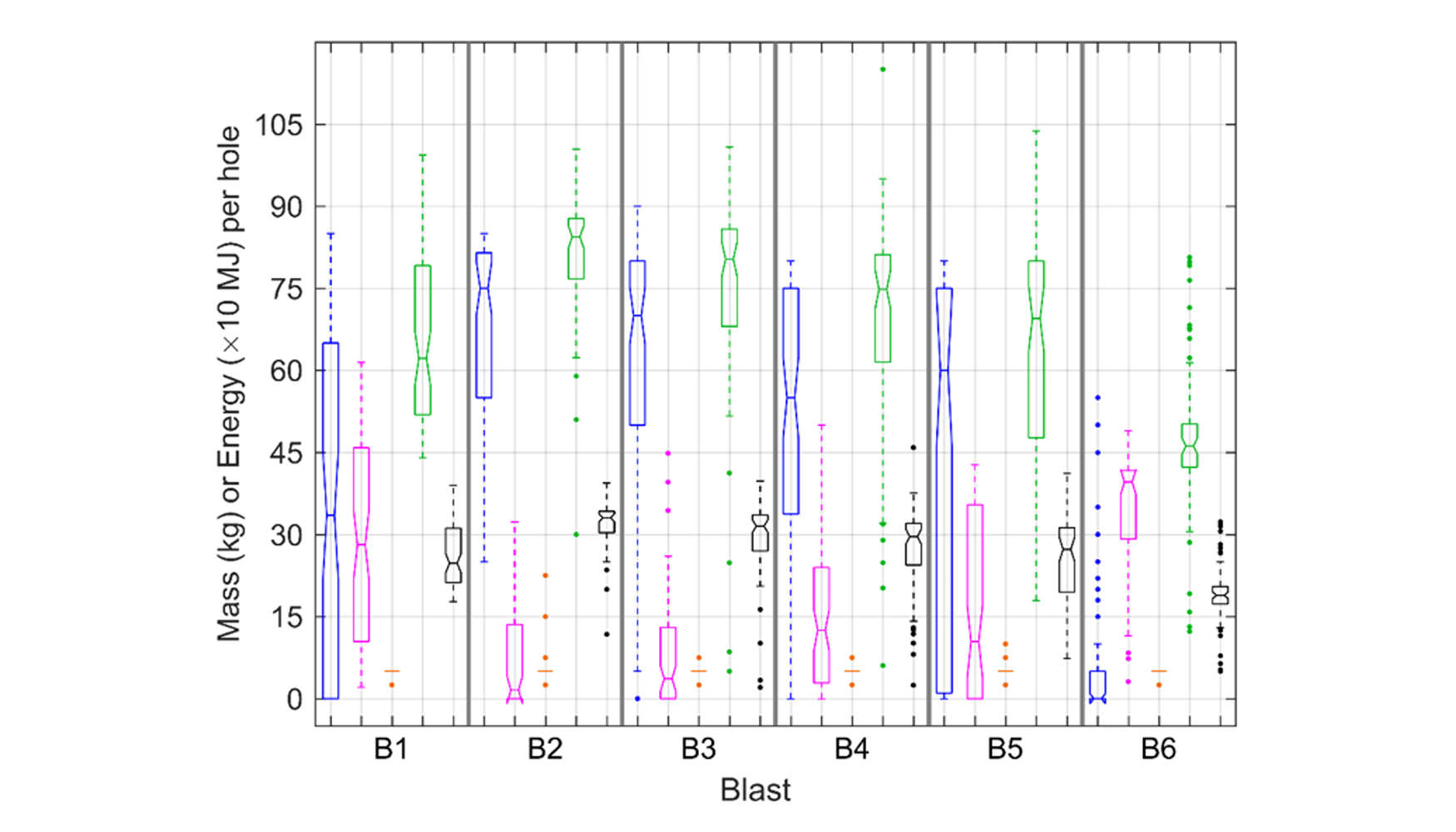
La cantidad de agua en los barrenos descrita cualitativamente en la Tabla 1, tiene probablemente un efecto limitado en la transmisión de la onda de choque, en la apertura de grietas y en la propagación de las fracturas (Singh and Narendrula, 2007, Zhang 2016) debido posiblemente a la muy baja capacidad de absorción de la milonita (0.10±0.03 %). Sin embargo, determina el patrón de carga de las voladuras; en el fondo como cebo se emplean siempre uno o dos cartuchos de 60 × 620 mm de dinamita (2,5 kg), mientras que cartuchos más pequeños de 50 × 380 mm (1,042 kg) se emplean hasta superar el nivel de agua. El resto de la carga se realiza con ANFO dejando una longitud de retacado de 2.5 m. En la Figura 2 se muestran las masas de explosivo empleadas por barreno en cada una de las seis voladuras: ANFO (cajas azules), dinamita (los cartuchos pequeños en color magenta y los grandes en color naranja), y el total (cajas verdes). La variabilidad en las cargas es muy limitada para los cartuchos de dinamita grandes puesto que se emplean como iniciadores (en la Figura 2 aparecen como líneas dada la baja variabilidad). La dispersión con el ANFO y la dinamita en cartuchos pequeños es grande; un caso extremo se observa en la voladura nº 6 donde 51 de 72 barrenos fueron cargados sólo con dicha dinamita (ver el valor cero de la mediana para la masa de ANFO en la Figura 2).

La variabilidad de la masa total de explosivo es, sin embargo, menor que la de los componentes individualmente. El valor de la energía total del explosivo en cada barreno se representa también como cajas negras en la Figura 2. La energía de la dinamita era de 4090 KJ/kg, mientras que la del ANFO es de 3893 KJ/kg (Sanchidrián et al., 2007). La distribución de la energía entre las voladuras es más uniforme que la distribución de las masas, lo que debería resultar en una variación limitada de la fragmentación dentro de la voladura, sobre el cual prevalece el factor medio de carga de cada voladura, de ahí la sensibilidad de los tamaños de los fragmentos.

Debido a la gran sobreperforación, el consumo específico total en masa varía entre 0,47 y 0,61 kg/m³ (ver Tabla 1). Estos valores parecen excesivos para el patrón de perforación empleado, y sugieren el empleo del consumo específico en masa por encima del piso (ratio de la masa de explosivo frente al volumen de roca descartando el explosivo que se encuentra en la parte sobreperforada del barreno) como un indicador mejor de la carga específica que contribuye a la fragmentación. Las voladuras con menor consumo específico se corresponden con una mayor cantidad de agua, o lo que es lo mismo, más producto encartuchado, mientras que valores altos de consumo específico se corresponden con menor agua o más producto a granel (ANFO). La razón para este fenómeno es que el producto encartuchado, que no rellena por completo el barreno, tiene menos explosivo que el producto a granel, que rellena por completo la sección, aunque la densidad del encartuchado sea mayor que la del producto a granel. La energía por unidad de masa en ambos productos no es muy diferente (como mucho un 5%), luego en masa, son casi intercambiables.

Las diferentes configuraciones de carga resultan en diferencias en la interacción explosivo-roca y su acople: el explosivo a granel está completamente acoplado a las paredes del barreno, mientras que el explosivo gelatinoso (en cartuchos) se ‘acopla’ a través de un anillo de agua. Trabajos como los de Ash (1973), Smith (1976), Brinkmann (1982) y Bleakney (1984) demuestran que el acoplamiento con agua es capaz de transmitir un choque de alta presión a la roca, por lo que su efecto en la fragmentación no difiere mucho de una carga completamente acoplada. Basándonos en esta idea, la acción del acoplamiento agua-explosivo a la roca es equivalente (con una ligera diferencia debido al cambio de energía específica y de masa) a un explosivo a granel (ANFO) directamente acoplado, rellenando por completo la sección del barreno.

La columna de explosivo se inicia desde el fondo con detonadores no eléctricos; con un retardo de 17 ms para los barrenos de la misma fila y 42 ms entre filas. Las voladuras se iniciaron en el centro o en un lateral de la primera fila empleando un patrón de disparo abierto (voladuras B2, B3 y B4) o cerrado (voladuras B1, B5 y B6) en chevron.

Tres básculas denominadas S1, S2 y S3, se instalaron en las zonas detalladas en la Figura 1, lo que ha permitido obtener dos puntos de la distribución granulométrica del material que entra en la planta. Del balance de masa en el circuito del primario, las fracciones de pase a 120 mm y 25 mm son:

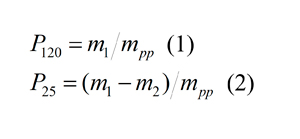
donde m_pp es la masa total de material procesado al dia:

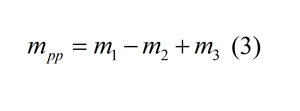
y m_k es la masa de material acumulado transportado por la cinta S_k por dia; esto se obtiene a través de una integración numérica del flujo de masa instantáneo a través del tiempo de trabajo de un dia de la planta.

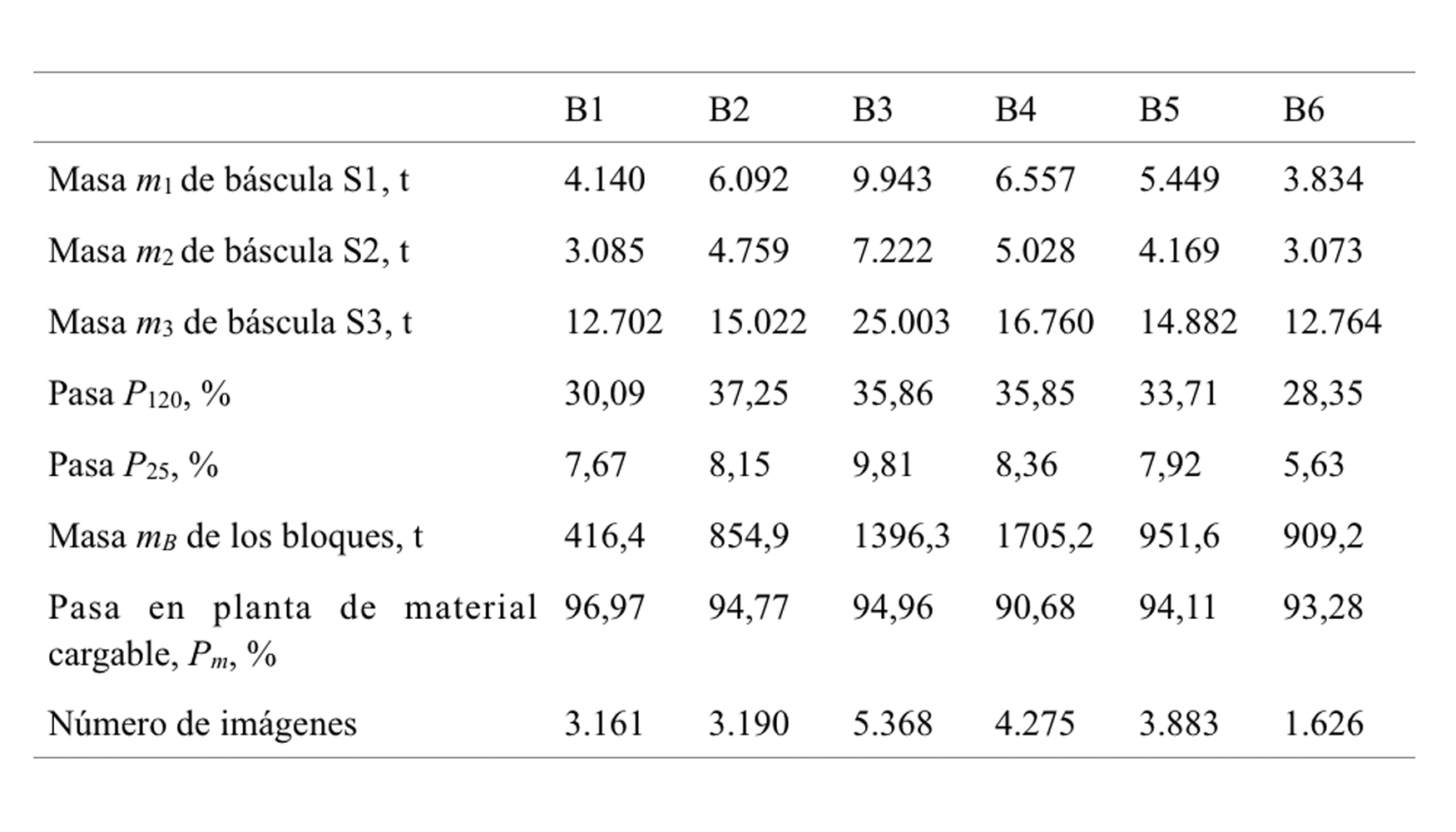
Notar que m_pp incluye los bloques de tamaño excesivo que se han roto mecánicamente, puesto que son transportados y procesados después de su fragmentación en cantera. Por lo tanto, despreciando la cantidad de material menor de 120 mm producido en la fragmentación de los bloques, P₁₂₀ y P₂₅ son fracciones de la masa generada post-voladura. La Tabla 2 resume los datos monitorizados en la planta. También muestra la masa de los bloques m_B determinados por la separación entre ‘pequeños’ y ‘grandes’, y sus tamaños medios estimados. La fracción de la voladura cargable se estima como: P_m = 1- m_B / m_pp.

El cálculo de la fragmentación se completó con el uso del sistema de análisis digital de imágenes online, Split-Online. Para obtener las imágenes del 'todo-uno' antes de la trituradora, una video cámara se instaló perpendicularmente por encima de la descarga del alimentador de la trituradora en la parte final de la rejilla (ver Figura 1). La fragmentación basada en imágenes es una medida del material mayor de 120 mm, con una pequeña proporción de finos, que en el punto de toma de imágenes no han pasado aún por la rejilla. El sistema no es capaz de delinear las partículas menores de 32 mm. Por debajo de este valor, la curva de fragmentación se ha estrapolado a través de una función de distribución analítica (Split Engineering 2010).

Las medidas de masa y curvas granulométricas a partir del análisis de imágenes se han asignado a cada voladura según las fechas en las que comenzaba y terminaba el escombro. Las granulometrías como medida del análisis de imágenes se han combinado en una distribución simple calculando el promedio de pase para cada tamaño de todas las distribuciones individuales de una voladura. La granulometría global del material volado se ha determinado a partir de los datos de las básculas, es decir, (25 mm, P₂₅) y (120 mm, P₁₂₀), y de los puntos base de las imágenes para tamaños mayores de 120 mm. El tamaño máximo de cada voladura es el mayor de la máxima medida. Sin embargo, dado que los bolos se habían roto previamente, estos no se han considerado como máximo tamaño de la voladura; de hecho, no se puede determinar percentiles mayores del P_m.

Se ha seguido el siguiente prcedimiento para construir la curva granulométrica:

• El rango de tamaño 25 mm ≤ x_j <120 mm se ha interpolado linealmente en un espacio log-log a partir de los datos de las básculas (25 mm, P₂₅) y (120 mm, P₁₂₀) para los mismos tamaños de puntos usados con Split. No se han extendido las distribuciones granulométricas por debajo de 25 mm dado que la cola de los finos (<25 mm) para las voladuras analizadas no se han medido.
• En el rango xj ≥ 120 mm, empezando desde (x₀, P₀) = (120 mm, P₁₂₀), los puntos sucesivos (x_j, P_j) se han calculado hacia arriba a partir de los puntos del análisis de las imágenes (x_j, P_j,_S) según:

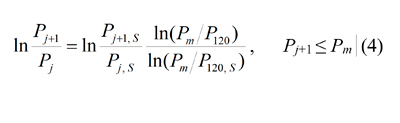
donde, P_120,S es el pasante de 120 mm desde la imagen analizada y P_m es pasante cargable (Tabla 2); la Figura 3 muestra las curvas de fragmentación de las medidas split sobre la parrilla (los puntos medidos se han representado con círculos) y las curvas finales determinadas a partir del procedimiento explicado arriba. Hay que tener en cuenta que las curvas de la rejilla tienen poca variación, al contrario que aquellas en las que se han usado datos ponderados. Las curvas finales de la Figura 3 se han extrapolado desde (x_m, P_m) hasta (2000 mm, 100%), aunque no se hace uso cuantitativo para ese rango.

Se ha ajustado una función Swebrec (Ouchterlony 2005, 2009) a la curva granulométrica final para evaluar la calidad del procedimiento, ya que esta función es generalmente la mejor distribución de componentes individuales de los datos de fragmentación cribados de la voladura (Sanchidrián et al. 2012a, 2012b, 2014). La forma analítica de la función de distribución acumulada de Swebrec es:

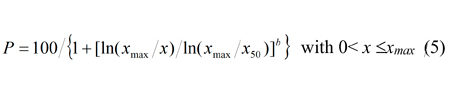
donde x_max es el tamaño máximo, x₅₀ el tamaño medio y b un parámetro de forma.

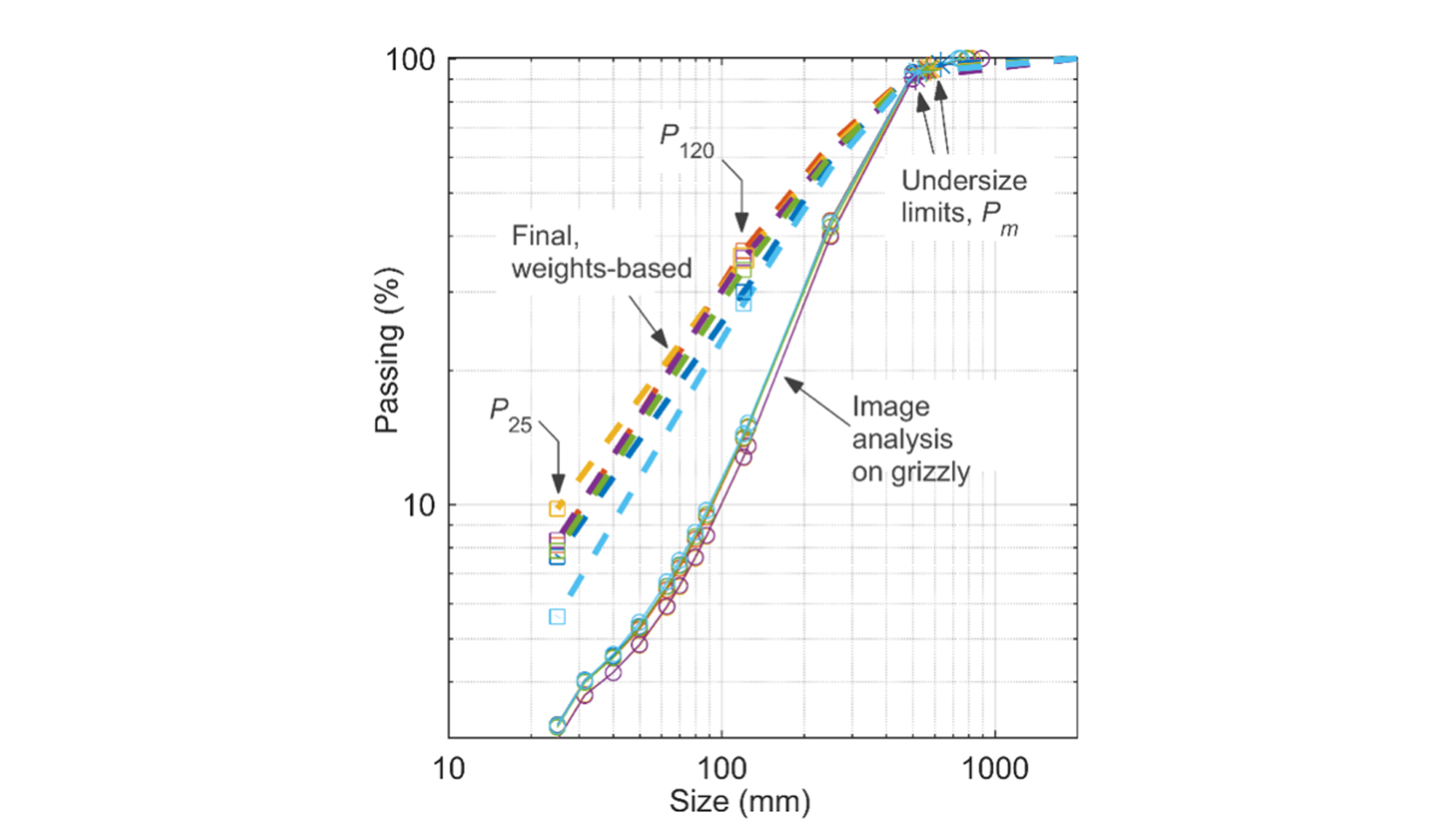
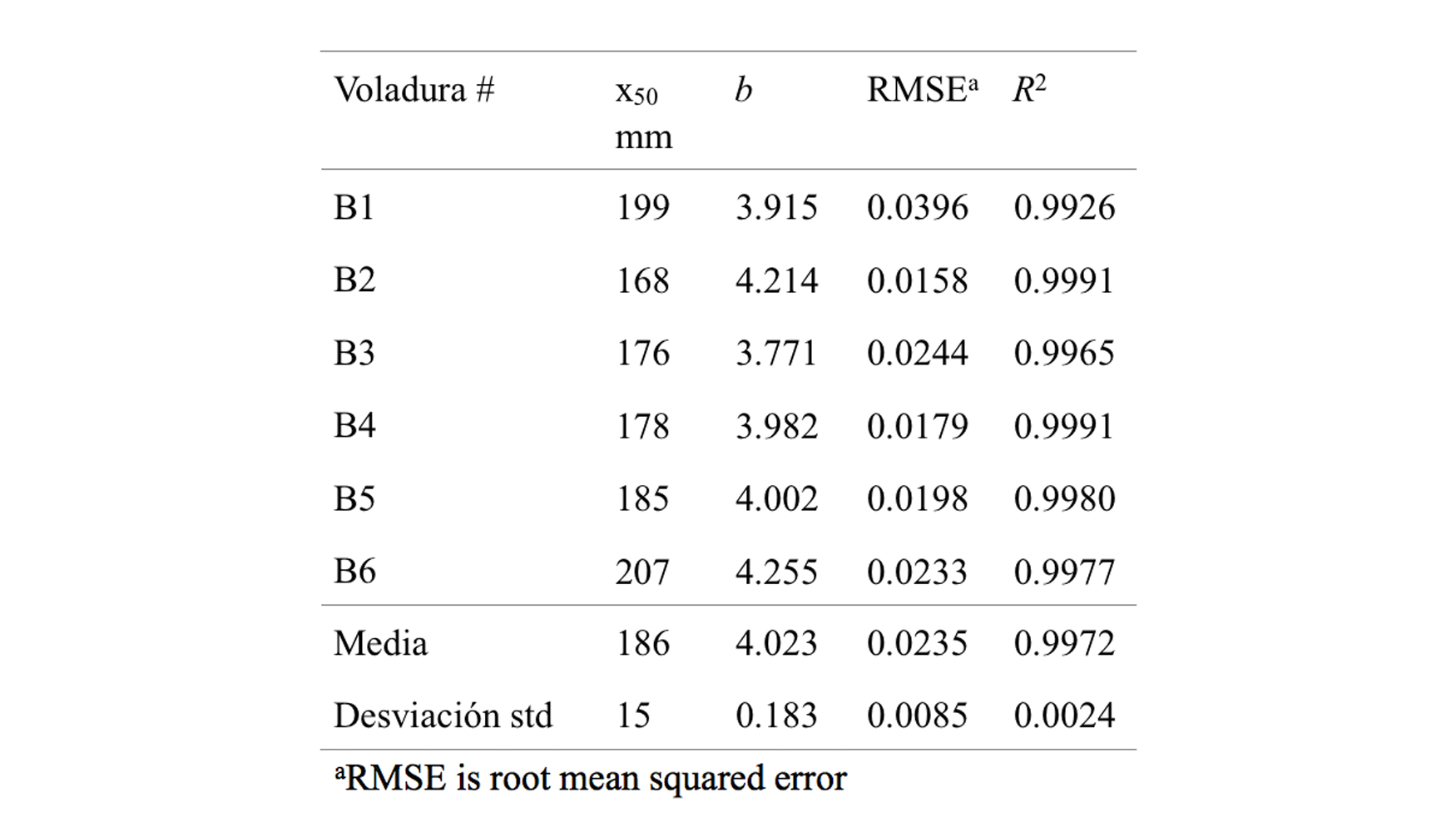
Los ajustes se han hecho para los rangos P₂₅ a P_m, fijando x_max en 2000 mm. La Tabla 3 resume los resultados del ajuste ponderado no lineal por mínimos cuadrados con pesos igual a 1/P_x². Se puede observar que el ajuste es bueno para todas las voladuras dado el alto coeficiente de determinanción mostrado en la Tabla 3 y, visualmente, en la Figura 7. Este resultado respalda la metodología desarrollada para construir la curva de distribución.

La fragmentación obtenida para factores de carga similares debería seguir el patrón del abanico de fragmentación-energía descrito por Ouchterlony et al. (2017). Esto significa que el tamaño del fragmento x_P (es decir, tamaño para el porcentaje P de material pasante) representado versus el consumo específico en una escala log-log, forma un conjunto de líneas convergentes en un punto focal (q₀, x₀). Según esto, cada percentil x_P se puede describir a través de una función potencial del consumo específico, con los parámetros A_P y α_P variables con la fracción pasante P:

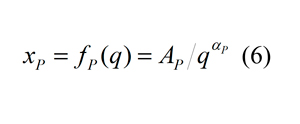
Como se indicó previamente, los percentiles mayores que P_m son inciertos por lo que, dado que el valor más bajo de P_m es 90.7% (ver Tabla 2), consideramos como válidas las curvas de fragmentación hasta P=90%. Los percentiles x_P, P=10, 20, …,90 se han elegido por medio de una interpolación lineal log-log de las curvas de distribución finales. La ecuacion 6 se ha ajustado en el espacio log-log para este conjunto de tamaños x_P, usando como q el consumo específico por encima del piso. Los coeficientes y los coeficientes de determinación se muestran en la Tabla 4; los valores a_P son repetidamente decrecientes según aumenta P, pero la línea de x₉₀ es casi horizontal y su pendiente no es significante; para los percentiles de 80 a 10%, los p-values de los exponentes son significatiovs o casi-siginificativos (para el percentil 30 son levemente superiores del límite 0.05). Para mejorar el ajuste se ha intentado una no-dimensionalización del modelo sieguiendo el trabajo de Ouchterlony et al. (2017), x_P/L_c siendo L_c una característica del tamaño de la voladura. El tamaño característico elegido es el utilizado en Sanchidrián and Ouchterlony (2017):

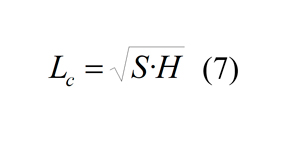
Donde, S es el espaciado entre barrenos y H es la altura del banco. La fómula utilizada para el percentile es:

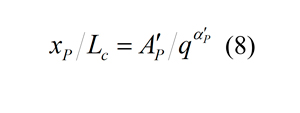
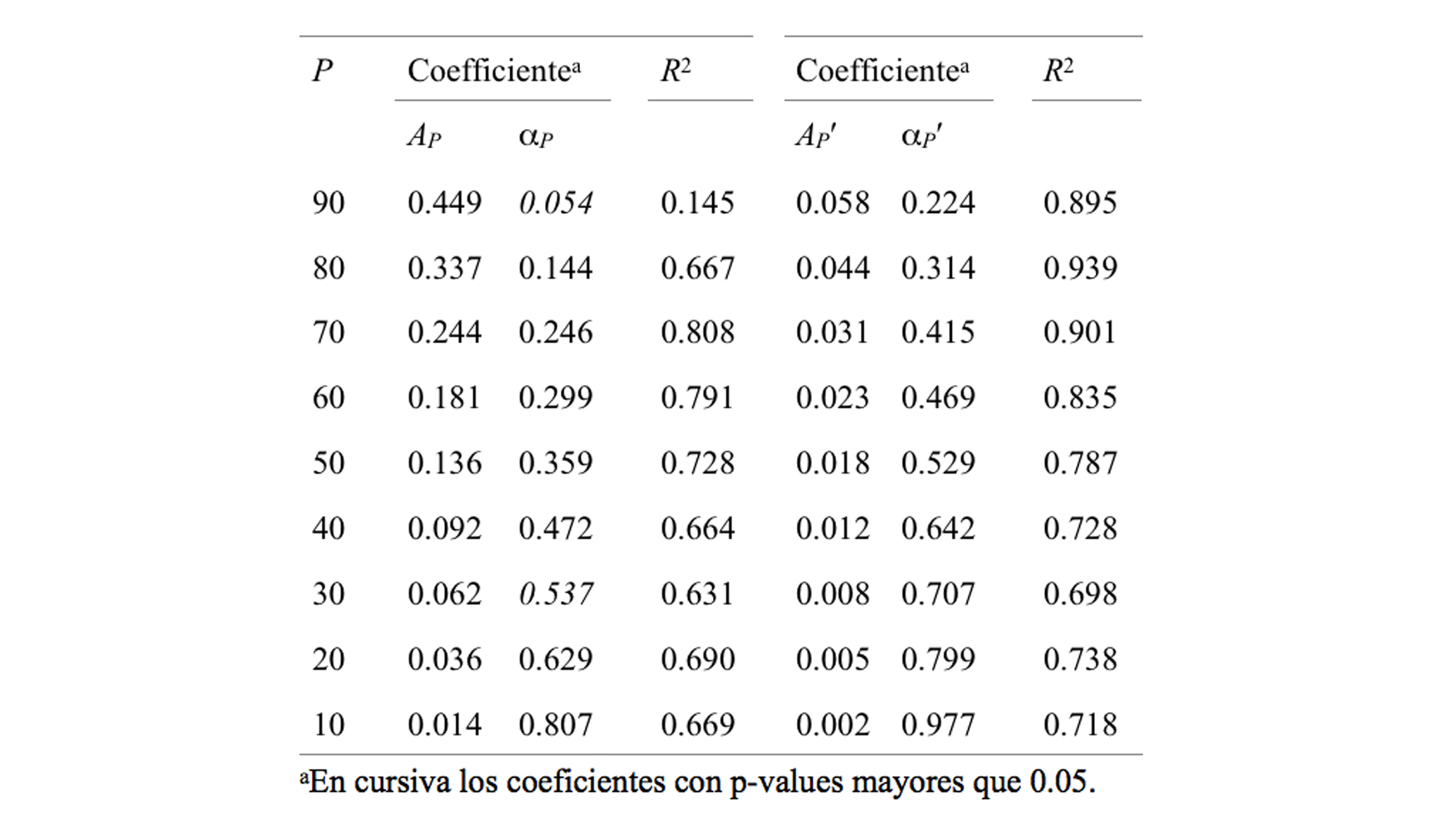
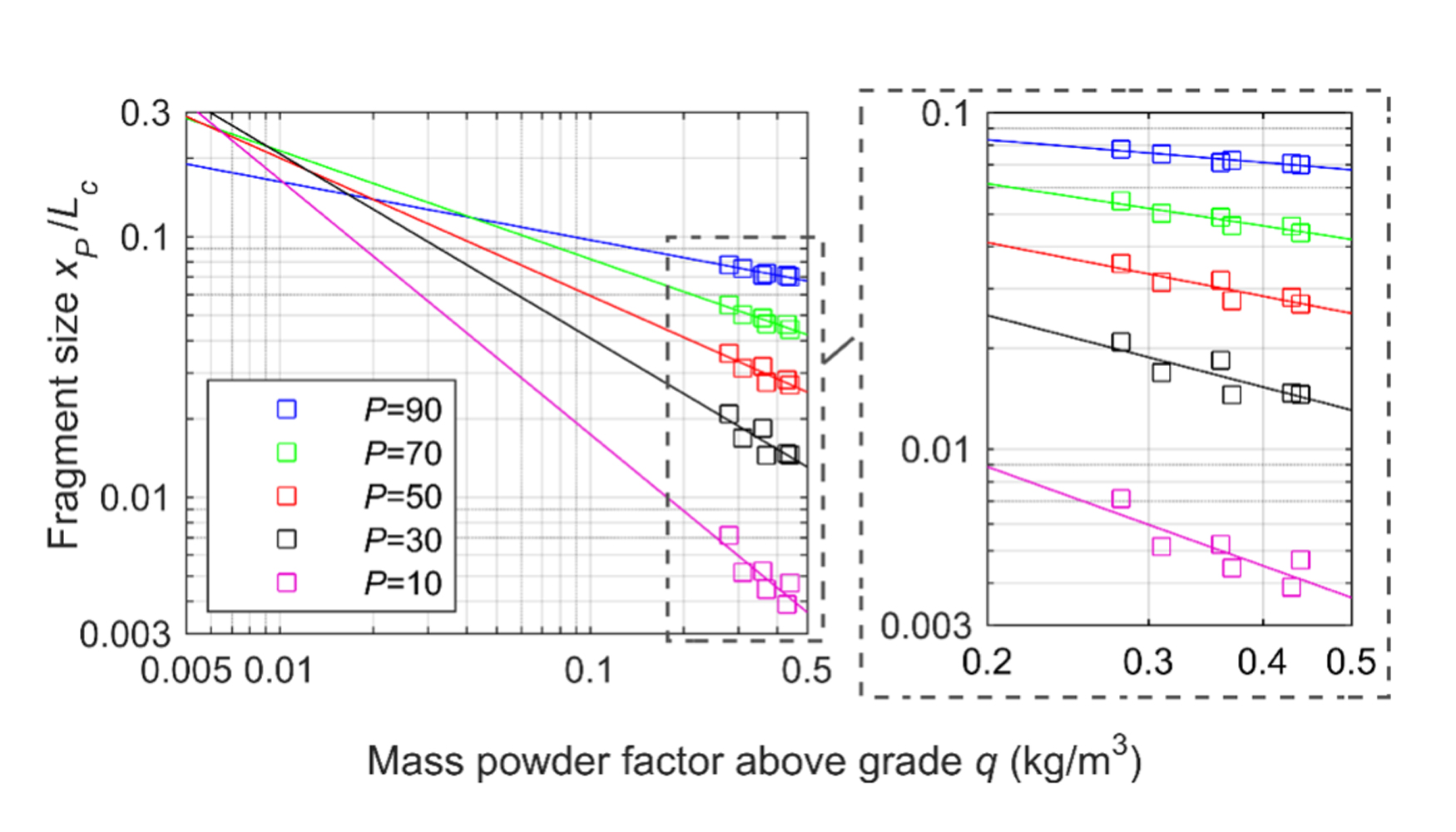
Figura 4. Tamaños de fragmento adimensionalizados x_P/L_c versus consumo específico en masa por encima del piso; en el gráfico de la derecha se representa ampliada la zona de datos.

Los resultados de este nuevo ajuste se muestran también en la Tabla 4 y en la Figura 4, donde los tamaños de los percentiles se representan versus el consumo específico por encima del piso. Los parámetros de todos los ajustes de los percentiles 10 a 90 son en este caso significativos a un nivel de 0.05, con los p-values de los coeficientes generalmente menores que los de la fómula dimensional. El coeficiente de determianción también aumenta en general, siendo su valor medio de 0.804. Los ajustes se han extrapolado a valores bajos de consumo específico para mostrar que convergen bastante bien a un punto en común, según los principios del abanico de fragmentación; la línea del 90% es, de alguna manera, discrepante, probablemente debido a que parece ser menos precisa para límites demasiado pequeños. Esto no esconde, sin embargo, que la fragmentación parece ser sensible al consumo específico por encima del piso, según los principios del abanico; vamos a mostrar que las coordenadas del punto focal se pueden determinar con una estadística significativa.

Con el objetivo de construir un modelo ingenieril, las funciones analíticas se han derivado para los coeficientes de la ecuación 8. El patrón del abanico enmarca la siguiente relación entre las pendientes α_P' y la fracción pasante cuando la fragmentación sigue la distribución de Swebrec (Ouchterlony et al 2017):

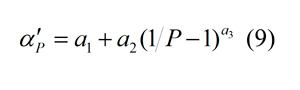
donde los coeficientes a₁, a₂ and a₃ tienen un significado físico: a₁= α'₁₀₀, a₂=α'₅₀ - α'₁₀₀ y a₃=1/b, siendo b el parámetro de forma de Swebrec, ver ecuación 5.

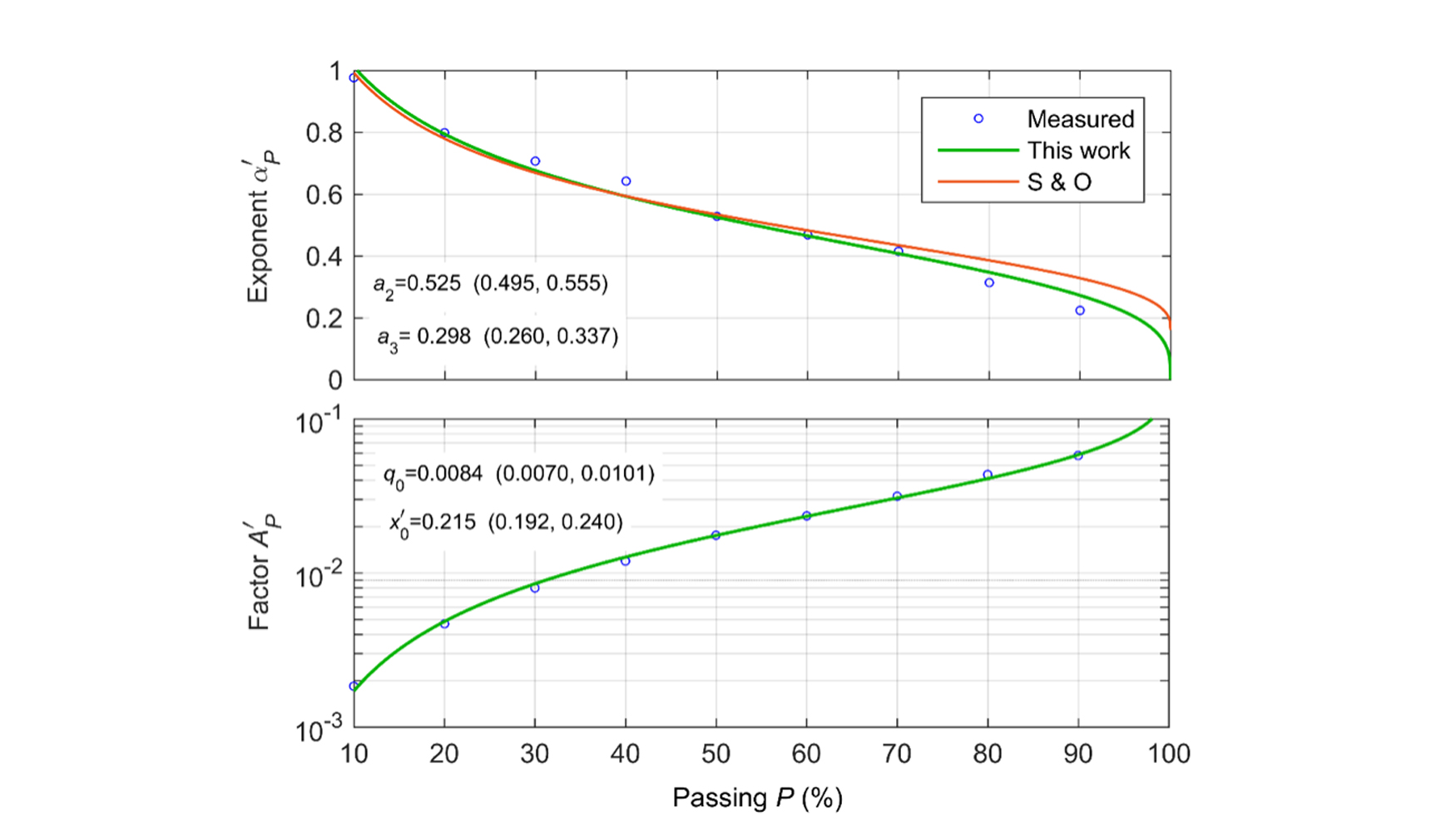
Esta función también trabaja satisfactoriamente para describir la fragmentación de un amplio conjunto de voladuras obtenidas mediante tamizado (Sanchidrián and Ouchterlony 2017). Los coeficientes a₁, a₂ y a₃ se han determinado por medido del ajuste de la ecuación 9 de las nueve pendientes α'_p para los percentiles P= 10 a 90 (ver Tabla 4). El coeficiente de determianción del ajuste es 0.997 y los coficientes a₂ y a₃ son significatios al nivel del 95%, pero a₁ no lo es. Esto significa que la pendiente de la línea del abanico del 100% (α'₁₀₀) es casi horizontal, sugiriendo que el tamaño máximo es independiente del consumo específico por encima del piso; este resultado es consistente (no podría ser de otra forma) dado el hecho de que el tamaño máximo de la voladura no se midió. Según esto, el coeficiente a₁ se ha eliminado del ajuste. La Figura 5 (gráfico superior) muestra la función ajustada para nuestros datos (línea verde) y los valores de los coeficientes y su intervalo de confianza; la relación entre valores predichos y medidos es buena (R²=0.982). La curva dada por Sanchidrián and Ouchterlony (2017), derivada del análisis de 169 voladuras se ha representado también para comparar (línea marrón). Las diferencias existentes entre ambas líneas aumentan según lo hacen los percentiles, principalmente debido al valor cero para el coeficiente a₁ obtenido en este trabajo. A pesar de todas las limitaciones de nuestros datos, se observa una similaridad remarcable.

Las propiedades del patron del abanico se pueden usar para obtener una expresión del prefactor en términos del porcentaje de pase. La ecuación general del abanico de energía se puede escribir como:

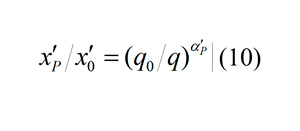
Donde se refiere a x_P/L_c y a x₀/L_c; La ecuación 10 también se puede escribir como:

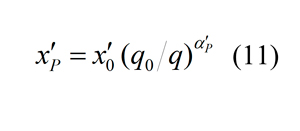
Comparando las ecuaciones 8 y 12 se obtiene que:

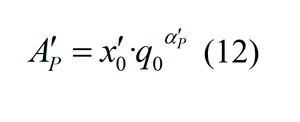
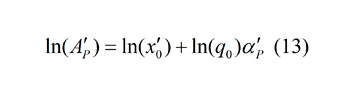
En la ecuación 13 se puede ver como función A'_p = f (P), ya que α'_p es en sí misma una función de P. Las coordenadas focales (q₀, x₀') se pueden determinar como parámetros del ajuste de la ecuación 13 a los nueve pares (A'_p,α'_p(P)). Según esto, el conjunto de los 18 parámetros que define el abanico (nueve pendientes α'_p y nueve prefactores A'_p, si se selecionan las nueve líneas del abanico) se reduce a cinco parámetros, q₀, x₀', a₁, a₂ y a₃. La Figura 5 (gráfico inferior) muestra los valores de A'_p (círculos azules) como función del pasante usando una escala logarítmiza para las coordenadas; la línea de regresión del ajuste de la ecuación 13 se ha representado también (línea verde), usando la expresión calibrada para α'_p en la ecuación 9. El coeficiente de determianción de este ajsute el 0.998 y los valores del punto focal (q₀, x₀') de las líneas del abanico son significativas al nivel de 0.05; estas y sus coeficientes de intervalo del 95% se dan en la Figura 5 (gráfico inferior).

El procedimiento seguido en este trabajo es (la notación prima se usa con parámetros adimensionales): i) a_P' y A_P' se obtienen para los percentiles P del tipo de ajuste empleado en la ecuación 8; ii) se ajusta la ecuación 9 para a_P' para obtener a₁, a₂ y a₃, y iii) se ajusta la ecuación 13 para los pares de A'_p, a'_p, a partir de los cuales se han obtenido la coordendas focales (q₀, x₀').

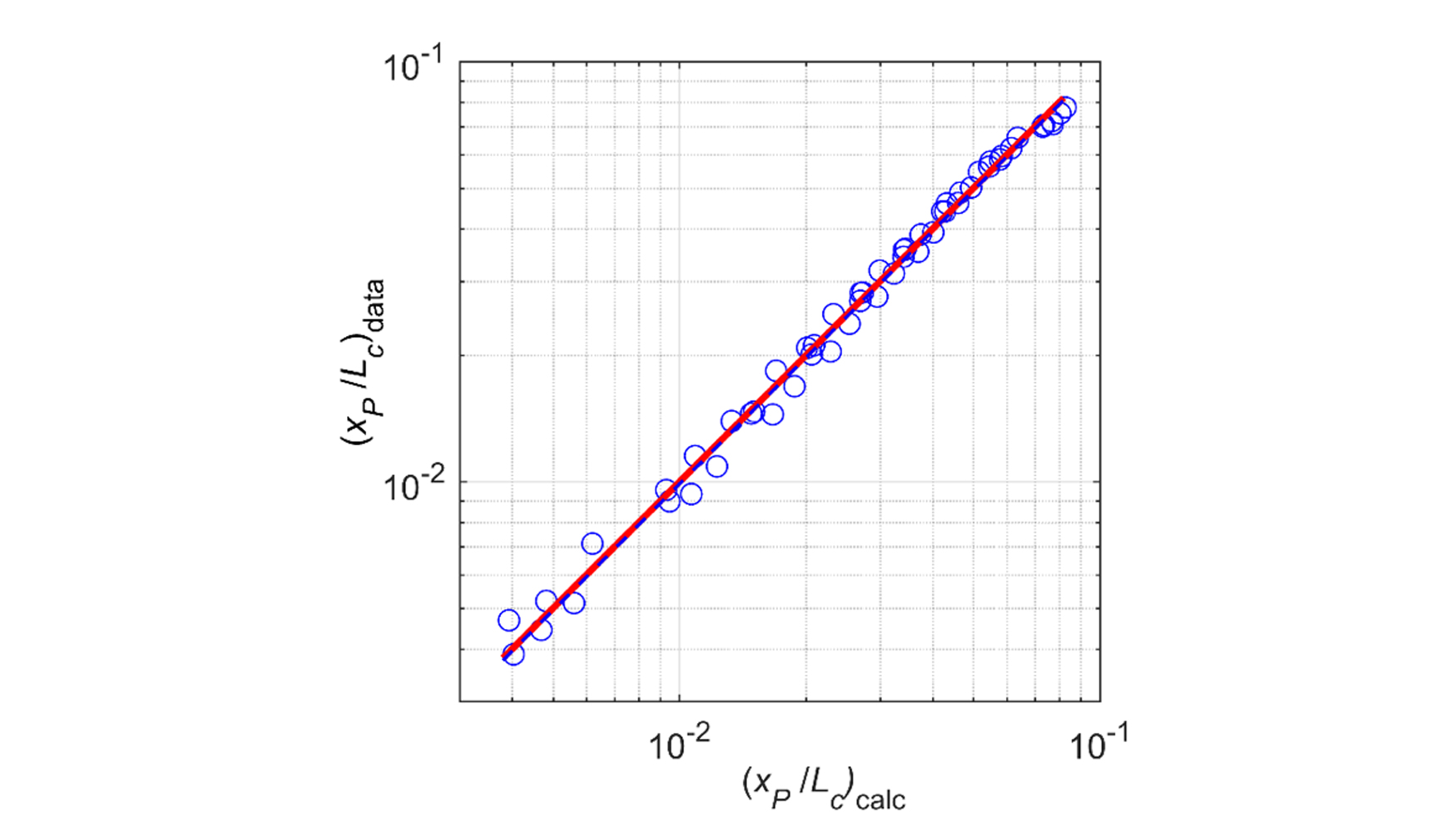
Los percentiles 10, 20, …, 90, determinados del modelo del abanico se han representado versus aquellos observados en la Figura 6; la línea discontinua azul es la regresión linear de los puntos y la línea roja se corresponde con los valores observados que son iguales que los calculados. El coeficiente de determinación es 0.992 y la pendiente de la línea ajustada tiene un 95% de cobertura, 0.975 a 1.002 (el término independiente se ha hecho cero ya que no es significativo para el nivel del 95%). Este resultado indica un buen funcionamiento del modelo en el rango de pasante de 10 a 90.

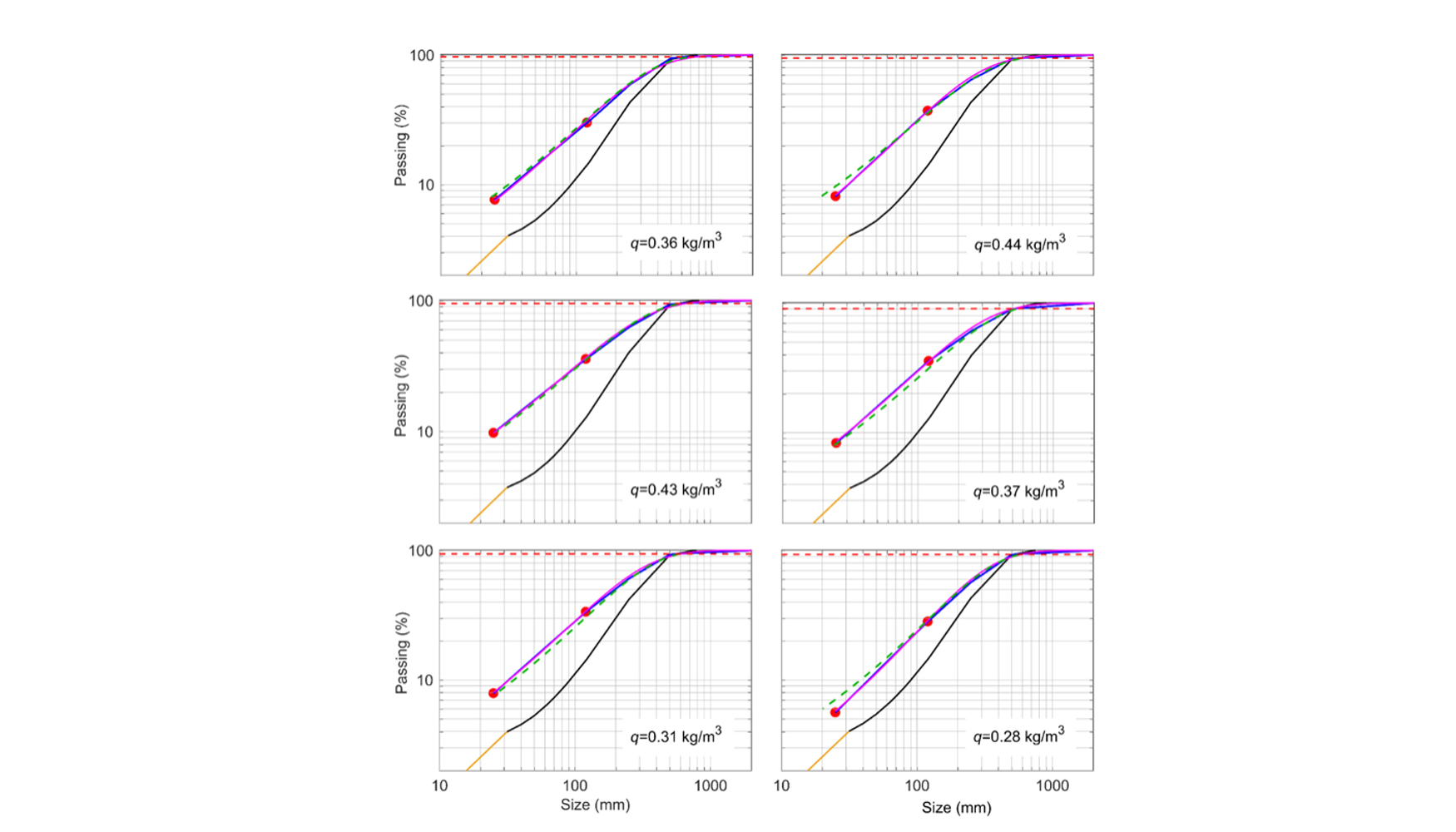
Los datos usados en este trabajo se dan gráficamente para cada una de las seis voladuras de la Figura 7; el consumo específico por encima del piso de cada una de las voladuras se muesta también en cada gráfico. En este, los puntos rojos son los pasantes a 120 y 125 mm de los datos de la báscula (Tabla 2); las líneas negras son los datos de las imágenes analizadas (naranja, datos extrapolados por debajo de la resolución del sistema, no usados); las líneas azules son las curvas de distribución calculadas; las líneas magenta son los ajustes de Swebrec de las distribuciones finales, y las líneas discontínuas verdes son las curvas de distribución obtenidas al aplicar el modelo del abanico de energía, ecuaciones 8, 9 y 12, a los consumos específicos por encima del piso. Estas se han extrapolado por debajo de los percentiles, de forma similar que para P₂₅, algo por debajo del 10% del pasante mínimo que fue utilizado para deducir las constantes del abanico de energía.

A partir de los principios del abanico de fragmentación-energía, se ha desarrollado un modelo de fragmentación por voladura para una cantera de milonita con una estructura de fracturación por bloques. El conjunto de datos comprende seis voladuras de producción situadas una detrás de la otra en el mismo bloque, por lo que la variabilidad en la resistencia de la roca y las características de macizo es limitada. El nivel de agua en los barrenos y el uso de explosivos (cartuchos de gelatina hasta superar la columna de agua y ANFO a granel a partir de ese punto) varía dentro y entre voladuras, pero la distribución de la energía del explosivo dentro de cada bloque es relativamente uniforme y el funcionamiento de ambos explosivos por unidad de masa es similar. La masa del consumo específico por encima del piso, considerado el mejor descriptor de la carga específica que contribuye a la fragmentación, oscila entre 0.28 y 0.44 kg/m³.

Se ha medido la fragmentación con tres básculas situadas en la planta de procesamiento, a partir de las cuales se ha obtenido la fracción de material pasante a dos tamaños, 120 (tamaño de corte de la rejilla) y 25 mm que se pueden calcular, y con un sistema online de imágenes digitales instalado sobre la zona de descarga de la rejilla de alimentación de la trituradora primaria. Esto permite evaluar el tamaño real de los bolos, cuya cantidad se ha estimado como el 3-9.3% del material. La distribución de tamaño del material volado se ha obtenido a partir del análisis de las imágenes digitales para el rango de partículas gruesas y utilizando las básculas para partículas entre 25 y 120 mm. La distribución de tamaño resultante está bien descrita por la función de Swebrec. La distribución de tamaños se ha interpolado para obtener el tamaño de percentil deseado en el rango donde los datos de la pila de fragmentación son representativos, es decir, sobre el 10 – 90% del material pasante.

El percentil de los tamaños de fragmentos de cada voladura, adimensionalizados por una longitud característica (la media geométrica de la altura del banco y el espaciado entre barrenos), forman un conjunto de líneas convergentes cuando se representan en función del consumo específico por encima en el espacio log-log. El prefactor y el exponente de las leyes potenciales del tamaño de fragmento con el consumo específico se han obtenido para nueve percentiles, de 10 a 90; los ajustes son todos significativos al 95%, proporcionando una buena descripción de la variabilidad de los datos con un coeficiente de determinación por encima de 0.70. La fórmula analítica para calcular la fragmentación como función del consumo específico por encima del piso se ha deducido de las expresiones para ambos parámetros del modelo (prefactores y exponentes) como función de la fracción pasa, según los principios del abanico de fragmentación-energía de Ouchterlony et al. (2017). Los 18 parámetros de las nueve líneas del abanico (nueve exponentes y nueve prefactores) se han reducido, de esta forma, a cinco: el punto focal de coordenadas del abanico y tres parámetros de la función de las pendientes con el porcentaje de pase.

El modelo explica el 99% de la variación en los tamaños no-dimensionales para percentiles entre 10 y 90 % y es estadísticamente significativo. Los errores máximos y esperados para los tamaños en ese rango de percentil son menores del 6 y 15%, respectivamente.

El trabajo experimental se ha financiado parcialmente por Maxam Civil Explosives ‘Cátedra Maxam’ (Project UPM/FGP 007033). Agradecemos también el apoyo de ARNO durante el desarrollo de todo el proyecto; nuestro especial reconocimiento al personal técnico de El Aljibe por su apoyo. Los autores agradecen también a Split Engineering su cooperación y apoyo. Finalmente, nuestro reconocimiento a los estudiantes que participaron en este trabajo.

Referencias

• Ash, R.L., 1973, “The influence of geological discontinuities on rock blasting”, PhD thesis, University of Minnesota, Minneapolis, pp 147-152.
• Bleakney, E.E., 1984, “A study on fragmentation and ground vibration with air space in the blasthole”, MSc Thesis, University of Missouri-Rolla.
• Brinkmann, J.R., 1982, “The influence of explosive primer location on fragmentation and ground vibrations for bench blasts in dolomitic rock”, MSc Thesis, University of Missouri-Rolla.
• Chung, S.H., Katsabanis, P.D., 2000, “Fragmentation prediction using improved engineering formulae”, International Journal of Blasting and Fragmentation 4:198–207.
• Cunningham, C.V.B., 1983, “The Kuz-Ram model for prediction of fragmentation from blasting”, Proceedings of 1st international symposium on rock fragmentation by blasting, Luleå Tekniska Universitet, Luleå.
• Cunningham, C.V.B., 1987, “Fragmentation estimations and the Kuz-Ram model—four years on”, Proceedings of 2nd international symposium on rock fragmentation by blasting, Society of Experimental Mechanics, Bethel.
• Cunningham, C.V.B., 2005, “The Kuz-Ram fragmentation model—20 years on”, Proceedings of 3rd world conference on explosives and blasting, European Federation of Explosives Engineers, UK.
• Departamento Técnico de Benito Arno e Hijos, 2005, “La cantera ‘El Aljibe’ en Almonacid de Toledo (Toledo)”, Rocas y Minerales 403:28-37
• Kanchibotla, S.S., Valery, W., Morrell S., 1999, “Modelling fines in blast fragmentation and its impact on crushing and grinding”, Proceedings of Explo’99—a conference on rock breaking, The Australasian Institute of Mining and Metallurgy, Carlton.
• Koshelev, E.A., Kuznetsov, V.M, Sofronov, S.T., Chernikov, A.G., 1971 “Statistics of fragments formed when solids are crushed by blasting”. Zh Prikl Mekh Tekh Fiz 2:87–100 (in Russian).
• Kuznetsov, V.M, 1973, “The mean diameter of the fragments formed by blasting rock”, Soviet Mining Sci 9:144–148.
• Ouchterlony, F., 2005, “The Swebrec© function, linking fragmentation by blasting and crushing”, Trans Inst Min Metall, 114:A29-A44.
• Ouchterlony, F., 2009, “Fragmentation characterization; the Swebrec function and its use in blast engineering”, Proceedings of the 9th International Symposium on Rock Fragmentation by Blasting, Taylor & Francis Group, London.
• Ouchterlony, F., Nyberg, U., Olsson, M., Vikström, K., Svedensten, P., Bergskolan i Filipstad, 2010, “Optimal fragmentering i krosstäkter, fältförsök i Långåsen”, Swebrec report 2010:2, Swedish Blasting Research Centre, Luleå University of Technology. (In Swedish).
• Ouchterlony, F., Nyberg, U., Olsson, M., Widenberg, K., Svedensten, P., 2015, “Effects of specific charge and electronic delay detonators on fragmentation in an aggregate quarry- Building fragmentation model design curves”, Proceedings of 11th international symposium on rock fragmentation by blasting, The Australasian Institute of Mining and Metallurgy, Carlton.
• Ouchterlony, F., Sanchidrián, J.A., Moser, P., 2017, “Percentile Fragment Size Predictions for Blasted Rock and the Fragmentation–Energy Fan”, Rock Mechanics and Rock Engineering, 50(4):751-779.
• Rosin, P., Rammler, E., 1933, “The laws governing the fineness of powdered coal”, J Inst Fuel, 7:29–36.
• Sanchidrián, J.A., 2015, “Ranges of validity of some distribution functions for blast-fragmented rock”, Proceedings of 11th international symposium on rock fragmentation by blasting, The Australasian Institute of Mining and Metallurgy, Carlton.
• Sanchidrián, J.A., Ouchterlony, F., 2017, “A distribution-free description of fragmentation by blasting based on dimensional analysis”, Rock Mechanics and Rock Engineering, 50(4):781-806.
• Sanchidrián, J, A., Segarra, P., López, L.M., 2007, “Energy components in rock blasting”, International Journal of Rock Mechanics and Mining Sciences, 44(1):130-147.
• Sanchidrián, J.A., Ouchterlony, F., Moser, P., Segarra, P., López, L.M. 2012a, “Performance of some distributions to describe rock fragmentation data”, International Journal of Rock Mechanics and Mining Sciences, 53:18-31.
• Sanchidrián, J.A., Segarra, P., López, L.M., Ouchterlony, F., Moser, P., 2012b, “On the performance of truncated distributions to describe rock fragmentation”, Measurement and analysis of blast fragmentation, CRC Press, Taylor & Francis Group, London, pp 87-96.
• Sanchidrián, J.A., Ouchterlony, F., Segarra, P., Moser, P., 2014, “Size distribution functions for rock fragments”. International Journal of Rock Mechanics and Mining Sciences, 71:381-394.
• Segarra, P., Sanchidrián, J.A., Navarro, J., Castedo, J, 2018, “The fragmentation energy-fan in quarry blasts”, Rock Mechanics and Rock Engineering, 51(7): 2175-2190.
• Singh, P., Narendrula, R., 2007, “The influence of rock mass quality in controlled blasting”, 26th International Conference on Ground Control in Mining, Morgantown.
• Smith, N.S., 1976, “Burden-rock stiffness and its effects on fragmentation in bench blastin”, PhD Thesis, University of Missouri-Rolla.
• Split Engineering, 2010, “Manual Split-Online en Español, Software Versión 4.02, Split Engineering Chile Ltda. Santiago, Chile.
• Thornton, D., Kanchibotla, S.S, Brunton, I., 2001, “Modelling the impact of rock mass and blast design variation on blast fragmentation”, Proceedings of Explo 2001, The Australasian Institute of Mining and Metallurgy, Carlton.
• Zhang, Z.X., 2016, “Rock Fracture and Blasting: Theory and Applications”, Elsevier, Oxford, pp 140-141.