Clasificación de muestras y detección de outliers en la caracterización geotécnica del terreno

La realización de una caracterización del terreno fiable comprende uno de los principales retos con los que la ingeniería geotécnica se enfrenta, al representar dicha caracterización una de las principales fuentes de incertidumbre en el proceso de diseño geotécnico y ser un factor determinante del mismo.

Los parámetros resultantes de la caracterización deben ser obtenidos bien de resultados de ensayos de laboratorio o bien de mediciones realizadas tanto en campo como en laboratorio, por lo que se deberá lidiar no sólo con la incertidumbre inherente a la variabilidad de las propiedades del propio terreno sino a otros factores que la incrementan como pudieran ser los posibles errores humanos o los errores de medición en los ensayos.

De este modo, tanto la variabilidad del propio terreno como el resto de factores añadidos muestran dicha incertidumbre asociada por medio de una dispersión más o menos amplia dentro de la muestra de resultados de ensayos de laboratorio o de mediciones de campo, generando desde agrupaciones de resultados entorno a ciertos valores hasta resultados que se alejan de la mayoría de los resultados, generalmente denominados ‘outliers’.

Estos hechos deben ser estudiados por medio de técnicas adecuadas que permitan gestionar la incertidumbre de manera correcta. Por ello, estos métodos deben ser capaces de determinar sus causas con el fin de establecer rangos de variación fiables y representativos de cada parámetro, evitando de este modo dar lugar a caracterizaciones no representativas que desvirtúen tanto los resultados medios como el cálculo de la dispersión y de los rangos de variación de dichos parámetros.

Simpson (2011) remarca la importancia de la acotación de los rangos de variación de los parámetros de cálculo dentro de valores esperables y suficientemente conservadores como un medio eficiente para evitar fallos en los diseños.

La obtención de rangos de variación de los parámetros geotécnicos representa una herramienta muy útil para acotar la variabilidad natural del terreno. Esta acotación permite establecer fácilmente los límites y variables de cálculo en métodos como Montecarlo o Rosenblueth.

De este modo, estos rangos de variación se deben establecer por medio del estudio de los resultados incluidos en la muestra, estableciendo unos límites superior e inferior adecuados a la realidad de los materiales estudiados.

El establecimiento de unos límites superior e inferior adecuados obliga a detectar tanto posibles ‘outliers’ que aumenten la dispersión de la muestra como agrupaciones de parámetros, así como las posibles causas que provocan dichos hechos para su posterior estudio en base a criterios geológico-geotécnicos, que llevarán a su inclusión o exclusión del estudio.

Una herramienta matemática que permite tanto la detección de outliers como de agrupaciones de valores es el denominado Lag Plot. Esta herramienta se selecciona por su sencillez de uso e interpretación, que se muestra a continuación.

3.1 ¿Qué es un Lag-Plot?

Un Lag-Plot es una representación gráfica que muestra si una serie temporal es aleatoria o, por el contrario, existe algún tipo de correlación en la misma. Este tipo de representación gráfica muestra la existencia de alguna estructura no aleatoria en los datos, lo cual indicaría que estos no podrían considerarse como aleatorios.

Desde un punto de aplicación de esta representación gráfica al campo geotécnico no se dispondrá de ninguna serie temporal, sino de datos provenientes de ensayos o mediciones; sin embargo, este tipo de muestras también pueden ser analizadas por medio de los Lag-Plot como se muestra a continuación.

Dentro del Lag Plot, se pueden distinguir dos series diferenciadas:

• Serie desordenada: comprende una serie compuesta por los ensayos colocados desordenadamente. Por regla general colocados según se encuentren en las tablas de caracterización. Muestra la aleatoriedad de los resultados. En este artículo se representa por medio de puntos rojos en todos los gráficos.
• Serie ordenada: comprende la serie de valores del parámetro ordenada de mayor a menor. Muestra las agrupaciones de valores y los posibles outliers y se representa como una sucesión más o menos lineal de puntos. En este artículo se representa por medio de puntos azules en todos los gráficos. Como se observa, es una representación lineal.

En el caso que concierne al análisis de datos objeto de estudio, ambas series se representan con un ‘lag’ o paso de valor 1 entre sus valores en el eje x, que contendrá los valores correspondientes a Xi+1 y el eje y donde se representarán los valores de Xi.

Esta notación corresponde al hecho que, una vez establecidas las series ordenada y desordenada, para su representación se deben colocar cada una duplicándola en dos columnas paralelas de n valores cada una. Para representar gráficamente los valores se tomarán parejas de valores tales que para cada valor i correspondiente al eje x le corresponda como pareja en el eje y el valor i+1 de la columna aledaña.

Esta no coincidencia de valores corresponde al denominado paso o ‘lag’ de valor 1. Es decir, a cada punto i de la primera columna le corresponderá el valor i+1 de la siguiente.

3.2 Usos del Lag Plot en el análisis de ensayos de laboratorio en Mecánica de Rocas

Generalmente, y desde un punto de vista puramente matemático, el Lag-Plot puede dar respuestas a las siguientes preguntas en el análisis de series temporales:

• ¿Son los datos realmente aleatorios?
• ¿Existe algún tipo de correlación en los mismos?
• ¿Cuál es el modelo adecuado para tratarlos?
• ¿Existen ‘outliers’ en los datos que se manejan?

Si el uso se centra en las aplicaciones geotécnicas, las preguntas que conciernen a esta aplicación corresponderían a la primera y a la cuarta, especialmente esta última.

A estas aplicaciones en geotecnia habría que añadirle la detección de agrupaciones de datos que deberán ser analizadas para determinar la causa de las mismas (diferentes litologías dentro de una misma unidad geotécnica, diferente grado de alteración o de calidad de la roca, diferentes laboratorios de ensayo, entre otros mucho ejemplos)

Como se ha comentado anteriormente, en el análisis de las series de datos provenientes de ensayos de laboratorio o mediciones de campo en mecánica de rocas, no existirá, en la gran mayoría de los casos, una serie de datos temporales que correlacionar entre sí, sino una lista de resultados de cada una de las muestras ensayadas.

Sin embargo, no es el propósito del tipo de estudio geotécnico propuesto establecer autocorrelaciones, ya que la finalidad del mismo será establecer tanto la existencia de valores fuera de rango como de posibles agrupaciones de datos que serán analizadas posteriormente en términos geológico-geotécnicos para establecer sus causas.

Por último, es extremadamente importante remarcar que su aplicación siempre debe realizarse primando el criterio geológico-geotécnico sobre el criterio matemático, que simplemente es utilizado como una herramienta auxiliar al conocimiento de los datos tratados y nunca como criterio único.

Un resumen de los usos de Lag-Plot con ejemplos de su uso es el siguiente:

a) Detección de outliers

La detección de outliers se realiza por medio de una inspección de la distribución de la serie ordenada. Al estar representada por una serie lineal de puntos, se podrá distinguir en la misma aquellos puntos que quedan alejados del cuerpo central de resultados, ya sea por encima o por debajo de estos. Un ejemplo se muestra a continuación:

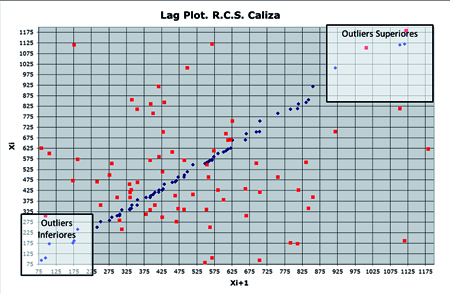
En cuanto a la localización de outliers, se pueden comentar los siguientes aspectos a tener en cuenta. Siempre será necesario la verificación de las causas de la desviación de esos puntos. Es decir, una vez localizados por medio del diagrama, se deberá siempre comprobar las causas de la misma para su eliminación de la muestra de datos a analizar.

Algunas de las posibles causas que causas dichas desviaciones pueden ser:

• Causas geológicas: los puntos corresponden a muestras cuya desviación puede explicarse por causas puramente geológico-geotécnicas (grado de alteración, calidad de la roca, presencia de fracturas en la muestra ensayada, etc.).
• Propia variabilidad del terreno: En este caso, los datos corresponden a muestras aisladas cuyos resultados divergen de la mayoría. En este caso se debe obrar con cautela e intentar buscar una causa geológica, ya sea puntual para dicha muestra o más general (muestra que pertenece a una zona de mala calidad poco estudiada o muestras con altos contenidos en carbonatos, hierro o cuarzo, por ejemplo). Por lo tanto, se debe determinar que dicha muestra no es representativa del global de la calidad global de la roca estudiada para su eliminación de la muestra que debe ser representativa de la misma.
• Errores humanos: tanto de medición durante el ensayo como a la hora de transcribir los datos (errores de escritura, de unidades, muestras pertenecientes a otras unidades que “se cuelan” por error, etc.).

b) Localización de agrupaciones de datos

Al igual que en el caso de los outliers, la serie ordenada también podrá representar agrupaciones de valores diferenciadas.

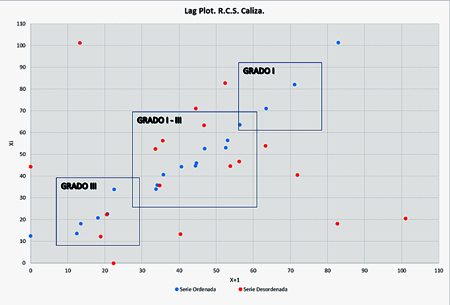
Al igual que sucedía en el caso de los outliers, las causas de dichas agrupaciones también deben ser estudiadas con detalle. Cabe destacar dos aspectos principales que, entre otros, pueden causarlas:

• Falta de muestras suficientes: en muestras con escaso número de ensayos o mediciones se pueden dar agrupaciones que al incrementar el número de ensayos se disipan al ser esta su causa.
• Causas geológicos-geotécnicas: Las agrupaciones pueden explicarse por su correlación con otro parámetro geológico-geotécnico. Los parámetros más útiles y con rápida correlación son el grado de alteración y/o el índice de calidad del macizo rocoso.

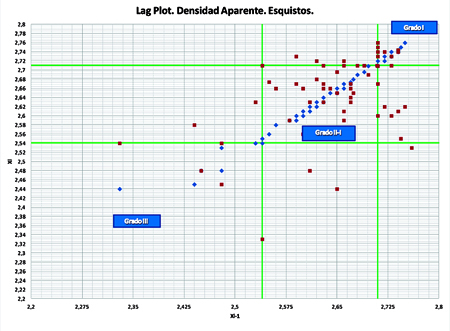
Por último, por medio de estas dos aplicaciones es posible establecer los rangos de variación de la muestra disponible. En primer lugar, al eliminar los extremos que desvirtúan los resultados de valor medio y de dispersión así como la distribución de la misma, se consigue establecer unos parámetros de cálculo limitados a unos valores realistas y justificados; por otro lado, al establecer agrupaciones de datos y darles una explicación geológica, permite tramificar los parámetros de una manera rápida, lo cual redundará en unos parámetros de cálculo más realistas para cada calidad del macizo rocoso.

Por ejemplo, al establecer diferentes agrupaciones, es posible establecer dentro de una misma distribución estadística general de una determinada unidad geotécnica los límites de valores que deben ser usados para cada calidad del macizo rocoso.

Entre los posibles métodos se proponen los siguientes métodos como métodos más usuales para el establecimiento de rangos de variación y detectar valores anómalos:

• Criterio de las 3 desviaciones típicas: este método conforma un método rápido para realizar una primera estimación de los rangos de variación. Se debe ser cauteloso, puesto que el método supone la distribución normal de la muestra y, al basarse en la media y la desviación típica, es afectado por los ‘outliers’:

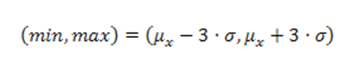
• Cálculo de valores anómalos: se basa en el cálculo de un límite inferior y un límite superior en base al rango intercualtílico definido por el primer y tercer cuartil de la muestra. Al igual que el anterior, es afectado por los propios outliers:

Como es conocido, existen otros métodos apropiados para el estudio de los rangos de variación y detección de ‘outliers’ como pueden ser los referidos al estudio de los residuos en una regresión lineal; sin embargo, desde el punto de vista de la simplicidad, de la rapidez de cálculo y de la facilidad de uso por medio de geotécnicos con pocos conocimientos en materia estadística, se entiende que estos son los más apropiados y de mayor uso.

4.1 Comparativa de los diferentes métodos propuestos y usos conjuntos.

La principal ventaja que ofrece el Lag-Plot sobre los métodos mencionados es que, al tratarse de una representación puramente gráfica y no necesitar calcular ningún parámetro a partir de los estadísticos de la muestra, este no se ve afectado por los propios outliers, como se ha comentado en el punto anterior que ocurre con las técnicas clásicas.

Debido a este punto, los métodos clásicos pueden dar lugar a valores máximos y mínimos incoherentes con la realidad –valores negativos, por ejemplo- para muestras de resultados con coeficientes de variación elevados (>50%). Al ser usuales estos coeficientes de variación en la práctica geotécnica, este constituye un punto a favor del uso de representaciones gráficas como el Lag-Plot frente a las otras formulaciones.

Asimismo, el Lag-Plot permite subdividir la muestra de resultados por medio de análisis de las posibles agrupaciones que puedan formarse.

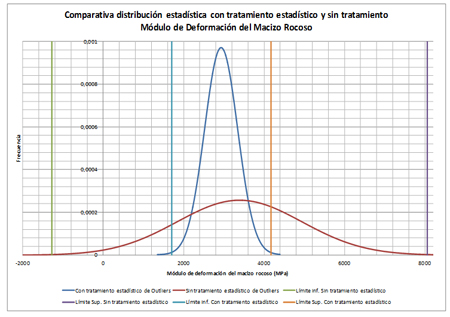
Para aclarar estos hechos se tomará como ejemplo una muestra con resultados de una campaña de investigación realizada en Granito cuya muestra de resultados reporta una distribución estadística incoherente por motivo de la influencia de los outliers.

Tanto la distribución resultante como los límites calculados por métodos clásicos se muestran a continuación:

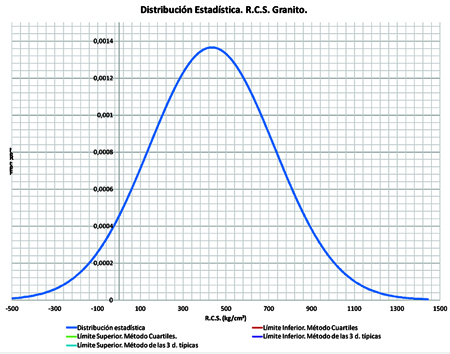
En este caso, debido a una serie de resultados muy elevados y algunos cercanos a 0, la desviación típica de la muestra es alta, lo que obliga a la distribución teórica a extenderse más allá de 0 y sensiblemente por encima del valor máximo registrado.

De igual modo, los límites calculados por métodos clásicos resultan o bien incoherentes o bien excesivamente elevados.

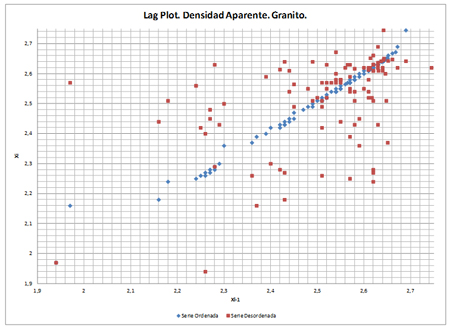
En el siguiente Lag Plot se puede observar la distribución de las muestras y sus valores mínimos y máximos. Como se observa, existe un grupo destacado de muestras con resultados muy elevados, siendo el resto, aparentemente, homogéneos:

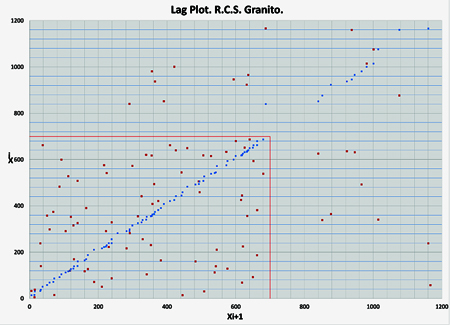
El problema de que una distribución se extienda más allá de 0 hacia valores negativos podría paliarse truncando la función de distribución y estableciendo que ningún valor pueda ser menor a 0 en el cálculo; sin embargo, partiendo de que se posee un número suficiente de muestras ensayadas, parece más razonable en vistas al Lag-Plot el investigar las causas de la agrupación de muestras superior, tomando como representativas las inferiores a 700 kg/cm², y, posteriormente, de la distribución de este subgrupo.

Una vez sacadas del análisis las muestras superiores, se provoca que la propia distribución varíe con respecto a la mostrada anteriormente. La comparativa con la anterior se muestra a continuación:

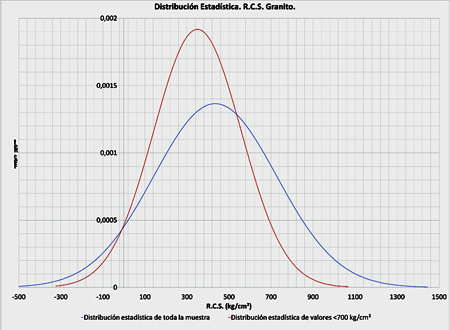
A pesar de ello, se sigue extendiendo más allá de 0.

Existiría la opción de usar la distribución Lognormal, que no permite valores menores a 0; sin embargo, en este caso, la distribución normal es la que mejor se ajusta a la distribución de la muestra –a excepción de valores pequeños -.

Si se continúa el análisis variando la escala del Lag Plot de manera que el máximo sea menor a 700 kg/cm² y se centra la atención en la mayor agrupación de muestras, el resultado es el siguiente:

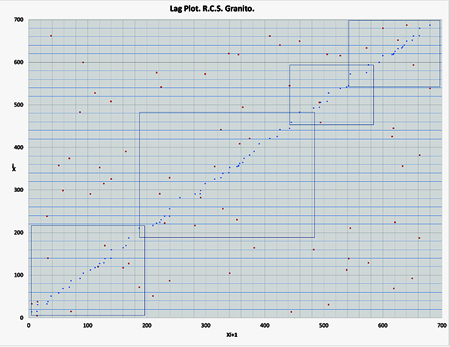
Como se muestra, a primera vista se pueden identificar 4 grupos diferenciados. Si se analizan estos grupos por grado de alteración se obtiene:

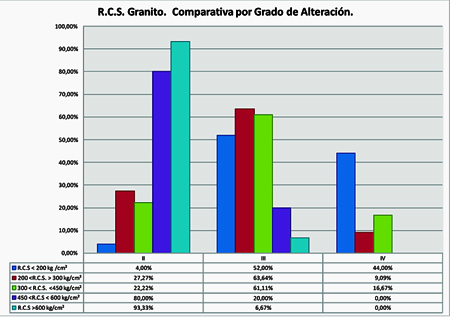
Como se observa, existen variaciones en la R.C.S según el grado de alteración, de manera que pueden establecerse 3 subdivisiones:

• Grado III – IV: R.C.S <200 kg/cm²
• Grado II – III 200 < R.C.S < 450 kg/cm²
• Grado II R.C.S > 450 kg/cm²

Obteniéndose las siguientes distribuciones:

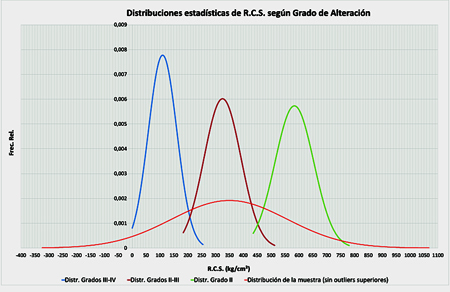
Únicamente se registran valores menores a 0 para una probabilidad menor a 0,01 en el caso de grado IV, por lo que se considera aceptable. Además, es posible gestionar los valores inferiores de la misma para reducir completamente este problema.

Asimismo, se ha conseguido segmentar la muestra según un posible índice de calidad del macizo, reduciendo la dispersión en cada tramo y englobando toda la distribución anteriormente calculada.

Cabe comentar que, según se puede observar en el gráfico, el valor medio de cálculo en el caso de la distribución global de la muestra correspondería a valores de grado de alteración III-II, pudiendo ser poco representativo del grado IV. Incluso el valor característico de esta muestra se encontraría por encima del límite superior de 3 desviaciones típicas de la distribución correspondiente al grado IV.

De este modo, se puede afirmar que, incluso el valor característico podría resultar un valor poco conservador en zonas de grado de alteración IV, lo cual refuerza la necesidad de segmentar la muestra de resultados de ensayos en función algún parámetro de calidad del macizo rocoso.

Cabe comentar que, al igual que se ha realizado la correlación con el grado de alteración, esta podría realizarse con cualquier indicador de calidad del macizo rocoso como el R.M.R., G.S.I, etc.

Por último, una vez establecidas estas distribuciones, se podrían establecer unos límites de cálculo superiores e inferiores por medio de los límites clásicos. En este caso se debería tener cuidado de que el conjunto de los intervalos de cálculo tengan en cuenta la globalidad de la muestra.

En el presente artículo se ha mostrado algunos de los posibles usos aplicados a la caracterización geotécnica del Lag-Plot como medio de detección de outliers y de clasificación de muestras y de conjuntos de las mismas.

En base a lo expuesto anteriormente, se pueden extraer las siguientes conclusiones:

El uso correcto de representaciones estadísticas gráficas como el Lag-plot permite una rápida y menos confusa determinación de valores fuera de rango, así como una detección de agrupaciones de valores más sencilla, rápida y visual.

El uso de estas técnicas requiere de experiencia, no sólo en su utilización, sino en la caracterización geotécnica en general. Su uso para la eliminación o agrupación de muestras sólo debe realizarse bajo un criterio basado en factores geológico-geotécnicos y no puramente matemáticos.

Asimismo, para una correcta utilización se debe conocer conceptos básicos de estadística, como el ajuste de funciones de distribución.

Su empleo resulta más sencillo, rápido y visual que el de los métodos clásicos expuestos, no siendo afectado por los propios datos, como sí ocurre en dichos métodos.

Por el contrario, es posible usarlo en conjunto con las técnicas clásicas mencionadas, ya que puede ser una técnica complementaria a las mismas.

Bibliografía

[1] Baecher. G, Chistian. John T. (2003). “Reliability and Statistics in Geotechnical Engineering”. Ed. Willey.

[2] Cochran, W.G. (1997) “Sampling techniques”. Ed. John Wiley &Sons Inc. Nueva York, Toronto (1997)

[3] Einstein, H.H. (1994): “Determination of rock engineering properties - objective and subjective assessment of uncertainty”. Keynote Lecture, Proc. 4th South American Congress on Rock Mechanics, Santiago de Chile.

[4] Fenton, G. (1997). Probabilistic Methods in Geotechnical Engineering Workshop presentado al “ASCE GeoLogan’97 Conference”, Logan, Utah. Julio 1997.

[5] Hoek, E. and Palmieri, A. “Geotechnical risks on large civil engineering projects” Keynote address for Theme I – International Association of Engineering Geologists Congress, Vancouver, Canada, September 21 to 25, 1998

[6] Simpson, B. (2011) Reliability in geotechnical design – some fundamentals. ISGSR 2011 - Vogt, Schuppener, Straub & Bräu (eds) - 2011 Bundesanstalt für Wasserbau

[7] Valley, B., Kaiser, P.K., y Duff, D. (2010). “Consideration of uncertainty in modelling the behaviour of underground excavations”. Proceedings of Deep Mining: 5th International Seminar on Deep and High Stress Mining, Santiago, Chile. Editado por M. Van Sint Jan and Y. Potvin. Australian Centre for Geomechanics. pp. 423-436.