Relación entre la medida de posición y el acabado de las piezas en las máquinas de control numérico
Uno de los problemas que más interés despiertan en el ámbito del mecanizado de piezas obtenidas con máquinas controladas con control numérico es el de la calidad de las mismas en cuanto a su precisión y acabado se refiere. Son muchas las variables implicadas en la calidad del mecanizado: bancadas, materiales, control numérico, motores, reguladores, algoritmos, dinámicas del sistema, estabilidad ambiental (vibraciones, humedad, temperatura), calidad de los sistemas de captación (cierre del lazo), etc. En esta presentación vamos a centrarnos en esta última variable siendo el objetivo del presente trabajo visualizar cómo la elección de uno u otro sistema de captación afecta directamente al acabado de las piezas mecanizadas. En particular se pretende relacionar la calidad y resolución de las señales proporcionadas por los sistemas de captación con el acabado de las piezas y ver cómo las pequeñas imperfecciones que puedan presentar dichas señales debido al montaje del sistema de captación o la calidad de las mismas afectan directamente al acabado de las piezas.
La distribución del trabajo es la siguiente: Presentación de un modelo teórico sencillo para la visualización de las señales proporcionadas por un sistema de captación, análisis teórico de la relación entre la calidad de las señales y el acabado de las piezas mecanizadas, presentación de algunos resultados experimentales, conclusiones y aspectos de mejora.
Desarrollo
Un codificador es un dispositivo capaz de determinar la posición relativa entre dos partes, una móvil y otra fija. Para ello se generan señales eléctricas que son enviadas a la zona de control del sistema para su tratamiento. Decimos que un codificador de posición es óptico cuando dichas señales eléctricas son generadas a partir de consideraciones ópticas. Al igual que cualquier otro aparato de medida, tiene dos características fundamentales: resolución y precisión.
- Resolución: Corresponde al mínimo incremento de la magnitud física que es capaz de resolver el sistema de medida.
- Precisión: Corresponde al error que se puede cometer al medir con el sistema de medida. Los codificadores ópticos se usan en procesos donde se requiere de un alto grado de precisión y resolución, como son los procesos de mecanizado de alta calidad. En principio, las resoluciones básicas que se obtienen con este tipo de codificadores se mueven en el entorno de las micras, si bien es posible interpolar las señales, pudiendo alcanzarse resoluciones de nanómetros. En cuanto a la precisión de los mismos, resaltar que ésta depende de varios factores como son el sistema mecánico, la calidad del grabado, el ajuste de las señales, etc. Matemáticamente las señales de un codificador de posición se pueden representar como:
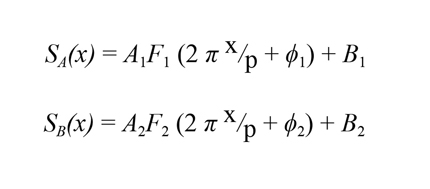
Donde x es la posición, p es el periodo de la regla, A1 y A2 son las amplitudes, B1 y B2 son los niveles de descentramiento (offset), φ1 y φ2 son los desfases entre las señales y, por último, F1 y F2 son las funciones que describen la forma de las señales. Idealmente estas señales deberían cumplir las siguientes condiciones:
- Las amplitudes son iguales A1 = A2 = A
- Los descentramientos son nulos B1 = B2 = 0
- El desfase entre señales es de un cuarto del periodo φ1- φ2 = π/2
- Las señales son senoidales F1 = F2 = sen
Si representamos la evolución de estas señales, una frente a otra, se obtiene el denominado diagrama de Lissajous que, en el caso ideal se corresponde con un círculo perfecto centrado en el origen. Dicho diagrama se repite cada periodo p de la regla. El codificador hace uso de dicho diagrama para realizar estimaciones de la cota posición a partir de las variaciones que presenta la fase existente entre ambas señales con el desplazamiento.
Factor de interpolación y acabado de piezas
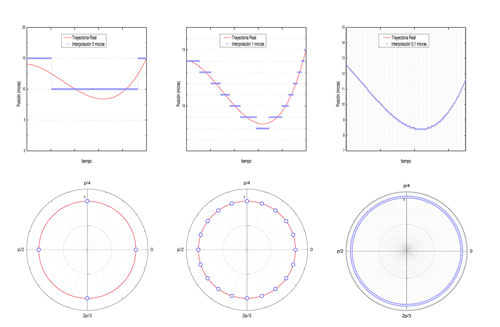
Denominamos factor de interpolación al número de sectores-divisiones que el codificador utiliza para discretizar el diagrama de Lissajous. En este sentido, decimos que dicho factor está estrechamente relacionado con el acabado de las piezas mecanizadas porque cuanto mayor sea éste, con mayor detalle y exactitud se reproducirá el círculo continuo teórico y por ello más exacto y detallado podrá ser el posicionado de la herramienta. Gráficamente podemos visualizar este hecho en el siguiente ejemplo simulado. La Figura 1 muestra una trayectoria a seguir (línea roja) y el posicionamiento de la herramienta proporcionada por un codificador óptico de 20 micras de paso cuando se considera una interpolación de 5, 1 y 0,1 mm. Bajo condiciones similares de trabajo, cuanto mayor sea el factor de interporlación, mejor se ajustará la herramienta a la trayectoria real y mejor será, por lo tanto, el acabado de la pieza.
Mostramos a continuación dos ejemplos reales.
Ejemplo 1: Realización de un círculo 3 m de radio manteniendo las mismas condiciones de trabajo salvo el codificador óptico. La Figura 2 muestra el círculo obtenido para 3 reglas Fagor —modelo S— con resoluciones de 0,5, 0,1 y 0,05 mm. En todos los casos se obtiene el círculo de las dimensiones deseadas, si bien el acabado de la pieza resulta más fino cuanto mayor es el grado de interpolación del codificador.
Ejemplo 2: La Figura 3 muestra datos reales de trayectorias recogidas por una máquina que utiliza una regla Fagor SAD (interpolación de 50 nm). El alto nivel de interpolación permite el seguimiento de trayectorias muy detalladas y finas.

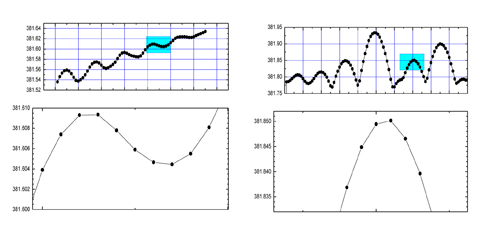
Figura 3: Ejemplo y detalle de trayectorias que pueden conseguirse con codificadores con un grado de interpolación de 50 nm —escala eje Y, en mm—.
Error subdivisional y acabado de piezas
Un codificador óptico es un dispositivo donde se ven involucradas diferentes tecnologías o disciplinas: Óptica, Electrónica, Mecánica, Software. En su proceso de fabricación, ajuste y montaje pueden darse situaciones de inhomogeneidades ópticas, de desajustes electrónicos debido a las tolerancias de los componentes electrónicos utilizados, tolerancias mecánicas de montaje, etc. Como resultado de todas las estas posibles incidencias, las señales proporcionadas por el codificador óptico podrán diferir ligeramente de las señales ideales en varios sentidos: las señales puede que no sean perfectamente sinusoidales, podrán aparecer descentramientos (offsets), desfases, cambios de amplitud, etc. Cuando esto ocurre el diagrama de Lissajous que se observa se separa del círculo “perfecto”. Si se aplica entonces el algoritmo de la arco-tangente punto a punto, se puede calcular y visualizar la diferencia entre la cota estimada por nuestro Lissajous y la cota estimada por el Lissajous ideal. Dicha diferencia es lo que se conoce como ‘error subdivisional’ y es inherente a todo montaje real.
Este error presenta un carácter periódico —periodo p de la regla— y afecta entre otros muchos aspectos a la dinámica general del sistema y por lo tanto al acabado de las piezas. A continuación mostramos algunos ejemplos simulados y experimentales.
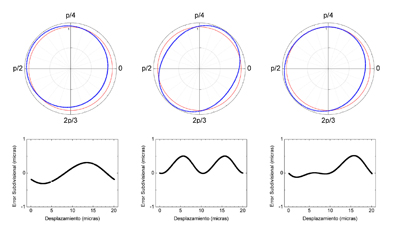
Consideremos situaciones en las cuáles el ajuste de las señales no ha sido perfecto y el diagrama de Lissajous no se corresponde con un círculo perfecto. Esto podemos simularlo introduciendo ligeros cambios en los parámetros de la ecuaciones mostradas con anterioridad.
La Figura 4 muestra tres ejemplos simulados tanto del Lissajous como del error subdivisional que se obtiene.
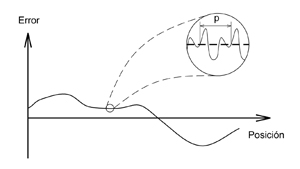
Es importante resaltar que este error se superpone a la gráfica de precisión proporcionada por los fabricantes (ver Figura 5).
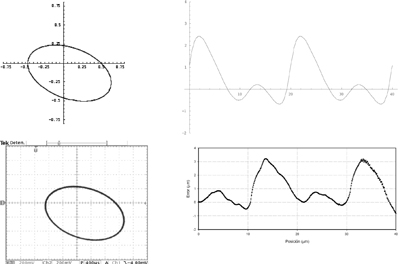
Hemos medido y constatado la existencia de dicho error. Los resultados se muestran en la Figura 6. Se considera un descentramiento del diagrama del Lissajous y se calcula el error subdivisional que le corresponde; se toma entonces un codificador óptico real y se desajusta hasta obtener un Lissajous similar al simulado. Se mide entonces la gráfica de precisión en un entorno muy pequeño ±p obteniendo así el error subdivisional real. Como puede verse, el acuerdo simulación-experimento es aceptable y clarificador.
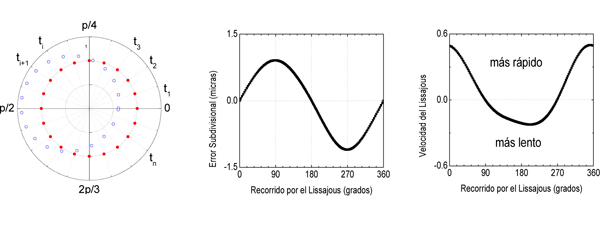
Consideremos una situación como las que se muestra en la Figura 7. Supongamos que el sistema se desplaza a velocidad constante y que, igualmente, existe una demanda de cota cada ciertos intervalos de tiempo ti equidistantes entre sí, por ejemplo, cada 125 micro-segundos. Bajo estas condiciones de trabajo, nuestro codificador, como consecuencia del error subdivisional proporcionará cotas más o menos adelantadas (puntos azules) con respecto a la cota ideal (puntos rojos). En otras palabras, es como si el codificador se adelanta o retrasara con respecto a la situación ideal o como éste no recorriera el Lissajous a velocidad constante sino que fuera más o menos rápido a lo largo de un periodo. Este efecto puede verse gráficamente en el propio Lissajous. El primer tramo de 5 primeras micras (primer cuadrante) es recorrido más rápidamente que los segundos y terceros tramos (segundo y cuarto cuadrante). Si representamos la derivada de error subdivisional podemos ver este efecto.
Si bien cada periodo p, el codificador mal ajustado da una vuelta completa al Lissajous y por ello no pierde contaje, es cierto que el Lissajous no es recorrido a velocidad constante sino que en unas zonas va más rápido que en otras. Este hecho afecta directamente a la dinámica del sistema, ya que ante constantes demandas de velocidad (62,5 microsegundos) y posición (125 microsegundos) el sistema reconoce ‘adelantos y retrasos’ indeseados que tiende a compensar afectando a la dinámica general del sistema.
Resumen y áreas de mejora
Los codificadores ópticos son los dispositivos preferiblemente empleados, por los fabricantes de máquina-herramienta, como elemento para la re-alimentación de la posición. La resolución y precisión con la que se determina dicha posición afecta al acabado de las piezas. En este trabajo nos hemos centrado en dos características de los codificadores: el factor de interpolación y el error subdivisional. Hemos visto como el primero afecta a la buena reproducibilidad de las trayectorias reales mientras que el segundo puede afectar directamente a la dinámica del sistema. El desarrollo de nuevas técnicas ópticas de interacción entre partes móviles, el tratamiento de las señales ópticas de manera conjunta —campo único—, el uso de fotodiodos estructurados y de componentes electrónicos de alta gama pueden ayudar a minimizar los efectos de descompensación y desajuste de las señales eléctricas y reducir así el error subdivisional. Aún cuando este está presente, es posible minimizarlo a partir de tratamientos software de las señales y de la implementación de algoritmos complejos.