Durante el proceso de fabricación de una pieza se inducen deformaciones plásticas no homogéneas, contracciones/dilataciones térmicas y transformaciones de fase que conllevan la aparición de tensiones residuales
Predicción de distorsiones generadas en el proceso de mecanizado de un componente de rodadura
Durante el proceso de fabricación de una pieza se inducen deformaciones plásticas no homogéneas, contracciones/dilataciones térmicas y transformaciones de fase que conllevan a la aparición de tensiones residuales. Estas tensiones están presentes en el material en ausencia de fuerzas externas debido a que existe un equilibrio interno de las mismas, es decir, están auto-equilibradas.
La mayoría de las piezas pasan por diferentes procesos de fabricación hasta obtener el producto final. Por tanto, suelen tener un historial de tensiones residuales que se va modificando durante los diferentes procesos, bien porque se les aplica un ciclo térmico, bien porque se elimina material o bien por otras causas.
Las tolerancias finales que estas piezas tienen que cumplir hace muy interesante la predicción de distorsiones que puedan causar los diferentes procesos. De esta forma, es posible aplicar medidas preventivas al comienzo del ciclo de desarrollo del producto controlando los tiempos de proceso y reduciendo el riesgo de perder la calidad del producto.
En el presente trabajo se han estudiado las distorsiones que se generan en la producción de un componente de un vehículo ferroviario, concretamente de una rueda de tren (ver figura 1). El objetivo primero ha sido conocer las causas reales de la distorsión que produce la falta de tolerancias tras el mecanizado final. El segundo objetivo ha sido plantear posibles alternativas a esas causas, que pueden pasar por cambiar las estrategias de mecanizado, modificar geometría de partida, …

Para obtener las distorsiones finales tras el proceso final de mecanizado se debe partir de un estado de tensiones residuales previo. En este caso concreto, se asume que las tensiones residuales son prácticamente generadas por el tratamiento térmico de temple anterior bajo la hipótesis de que el material está libre de tensiones al final de la fase de calentamiento.
De esta manera, primero se ha obtenido el campo de tensiones residuales simulando el proceso de temple. Luego se ha simulado el proceso de mecanizado usando una metodología simplificada basada en la eliminación de material. Esa eliminación no sólo altera la microestructura sino que también perturba el equilibrio de tensiones residuales de todo el volumen dando lugar a distorsiones para que lleguen de nuevo a auto-equilibrarse.
1. Simulación del proceso de fabricación
Tal y como se ha comentado anteriormente, la simulación de las distorsiones finales requiere tener en cuenta todo el historial aguas arriba. Ello implica la necesidad de simular todos los procesos importantes influyentes en su estado de tensiones residuales. Todas las simulaciones se han llevado a cabo utilizando el software de elementos finitos Abaqus. Al tratarse de una geometría de revolución, se han utilizado modelos axisimétricos en las diferentes simulaciones realizadas.
1.1. Proceso de fabricación
El proceso de fabricación de la rueda de tren se puede resumir mediante el flujo de diagramas mostrada en la figura 2. Tal y como se observa, su fabricación consta de cuatro fases principales en las cuales se van creando y modificando las tensiones residuales.
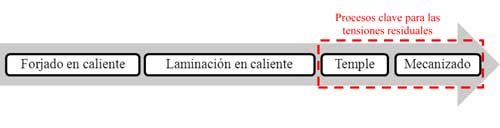
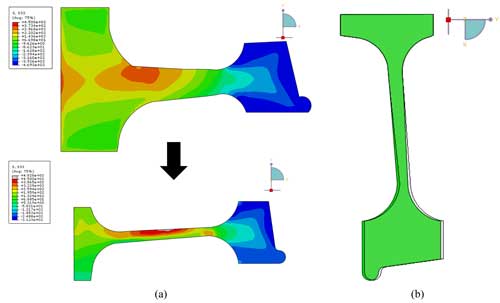
El proceso empieza con el forjado en caliente donde se le da una preforma al bloque inicial de acero. Estas preformas son laminados en caliente para obtener el perfil de la rueda tal y como se observa en la figura 3a. Luego se le da el temple mediante diferentes chorros de agua en el extremo del mismo con el objetivo de conseguir las propiedades mecánicas deseadas. Esto hace que no sea posible plantear tratamientos de alivo de tensiones. Para finalizar, se realiza el mecanizado final mediante torneado con el que se logra la sección de la figura 3b.

Se puede hacer la hipótesis de que los procesos principales que influyen en las distorsiones finales son el temple y el mecanizado ya que las tensiones de forja y laminación son eliminadas en gran medida durante el calentamiento a la temperatura de homogeneización. Basándose en ello, en los apartados siguientes se explica en qué consiste la simulación de cada uno de ellos.
1.2. Simulación del tratamiento de temple para la determinación del estado de tensiones residuales inicial
Bajo la hipótesis de que los procesos anteriores son despreciables para la predicción de las distorsiones, se ha simulado el proceso de temple partiendo por la geometría obtenida tras la laminación en caliente (figura 3a). Esta geometría ha sido obtenida por sistemas ópticos de medición basadas en la triangulación del haz laser. Así, se ha obtenido la sección de la rueda después de la laminación.
Para saber el estado tensional tras el temple, se ha llevado a cabo una simulación termo-mecánica desacoplada.
1.2.1. Modelo térmico
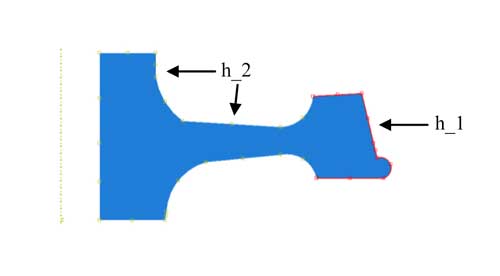
En primer lugar, se ha realizado la simulación térmica. La pieza es enfriada desde la temperatura de homogeneizado de temple. Como el templado se realiza por medio de diferentes chorros de agua, estos se han modelizado utilizando varios coeficientes de convección en las diferentes zonas de la pieza. Concretamente, se han diferenciado dos zonas tal y como se puede ver en la figura 4. El coeficiente h_1 utilizado en la zona de rodadura (zona roja) es bastante mayor que la utilizada en las demás superficies (h_2).
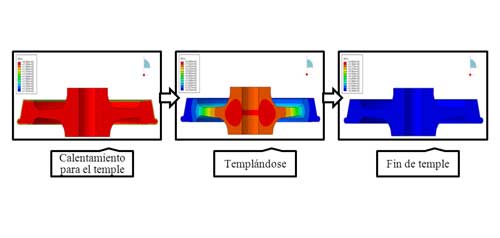
En la figura 5 se puede ver la evolución de la temperatura durante la simulación del temple. Como se observa, la pieza se enfría desde la zona de rodadura hacia dentro. Como el enfriamiento no es homogéneo la pieza queda tensionada al final del proceso.
1.2.2. Modelo mecánico
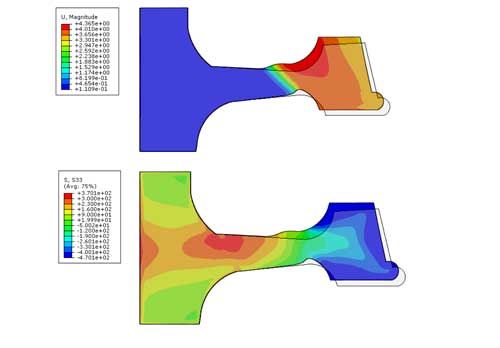
En este modelo, se toma como input el campo de temperaturas transitoria calculada en el anterior análisis, y teniendo en cuenta las propiedades mecánicas del material en función de la temperatura, se ha obtenido un estado de tensiones residuales y distorsiones final correspondiente al proceso de temple. En la figura 6a se observa la distorsión que sufre la geometría laminada inicial al final del temple. La dirección principal de contracción es la radial. En cuanto a las tensiones residuales, en la figura 6b se pueden ver las tensiones tangenciales que quedan en la pieza al final del proceso. En cuanto a la magnitud de las mismas, se observa que son cercanos al límite elástico. Se puede ver también que debido al proceso de temple específico, se consiguen inducir tensiones residuales de compresión en la zona de rodadura, las cuales son equilibradas por las tensiones tractivas de la pieza restante.
1.3. Simulación simplificada del proceso de mecanizado
Partiendo de la geometría y el estado de tensiones residuales final del proceso de temple, se ha realizado el mecanizado de la pieza con el fin de obtener la geometría final requerida.
Se pueden diferenciar dos niveles de la simulación del proceso de mecanizado acorde al objetivo que se quiere lograr:
i. Simulaciones a gran escala (eliminación del material): se modela la eliminación del material con el objetivo de predecir las distorsiones finales debido a la redistribución de tensiones que se da. En estos modelos se elimina el volumen equivalente pudiendo tener en cuenta indirectamente las fuerzas y calentamientos que produce el propio proceso [1]. Esa eliminación se efectúa mediante la eliminación de los elementos correspondientes al volumen eliminado en cada paso.
ii. Simulaciones a pequeña escala (formación de la viruta): se centran en simular la formación de la viruta pudiendo analizar las fuerzas de corte, tensiones, temperaturas, desgastes, … pero siempre a un nivel muy local.
Ya que el objetivo final es la predicción de las distorsiones, en este caso se ha llevado a cabo una simulación a gran escala, asumiendo las hipótesis que se hacen en dicho método. Tal y como se reporta en la bibliografía [2] - [3], las tensiones residuales causadas por la formación de la viruta afectan especialmente a la superficie de la capa mecanizada. En particular, los resultados experimentales reportados en [4] sugieren que las tensiones residuales inducidas por el proceso de mecanizado están limitadas a una región con una profundidad máxima de 150-200m. El efecto del mecanizado en el material base es prácticamente nulo. Como las tensiones residuales inducidas por los anteriores procesos se distribuyen en todo el material, es posible considerar las tensiones residuales del mecanizado como despreciables. Por esta razón, el proceso de mecanizado se puede ver como un proceso de relajación de tensiones por la eliminación del material y cambio de rigidez de la sección. Esta metodología de simulación de distorsiones por el mecanizado se explica más detalladamente en [4].
Como se observa en la figura 3b, todo el material correspondiente a la sección coloreada en azul debe ser eliminado para obtener la forma final. La eliminación de ese material se puede hacer en diferentes secuencias siempre y cuando se tengan en cuenta las limitaciones que pueda haber (limitaciones de la máquina herramienta, accesibilidad de la herramienta, tiempo de ciclo, …) y los requerimientos que deba cumplir en cuanto a calidad (tolerancias superficiales, tolerancias geométricas, …).
Al tratarse de un modelo axisimétrico, en cada paso se elimina un disco correspondiente a la sección definida. Esa aproximación es correcta debido a que en el torneado de la pieza las velocidades de giro son lo suficientemente elevadas para despreciar la respuesta tridimensional.
1.3.1. Análisis de la secuencia actual de mecanizado
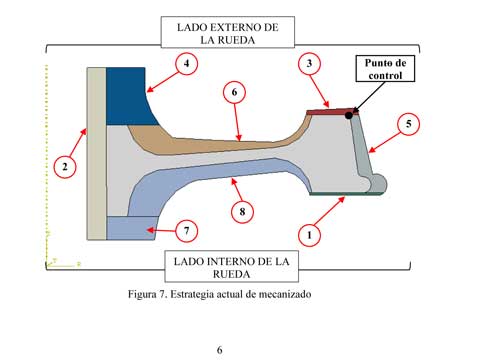
La estrategia actual de mecanizado se resume en las siguientes operaciones (figura 7):
- Mecanizado del lado interno del aro
- Mecanizado del orificio del cubo
- Mecanizado del lado externo del aro
- Mecanizado del lado externo del cubo
- Mecanizado del lado externo del friso y de la superficie de rodadura
- Mecanizado del lado externo del disco
- Mecanizado del lado interno del cubo
- Mecanizado del lado interno del disco
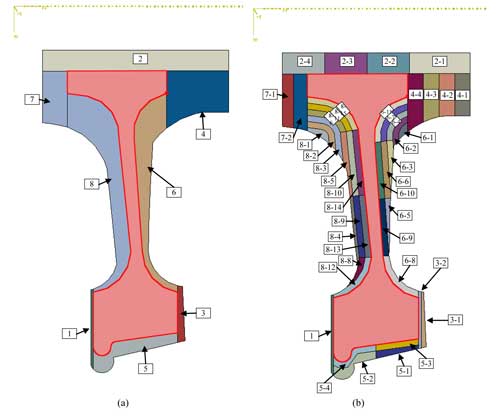
El volumen a eliminar en cada operación se puede discretizar en diferentes dominios para la simulación del mecanizado. Primero se ha analizado el efecto que tiene el grado de discretización en las distorsiones finales. Para ello, se ha simulado la secuencia actual de mecanizado con dos densidades diferentes tal y como se puede ver en la figura 8. La secuencia de las operaciones es la misma que la explicada arriba. Con la discretización 2, además de la secuencia de operaciones, en cada operación se puede considerar el orden en que se elimina el material. Por ejemplo, en caso de la operación 2 de mecanizado del orificio, los dominios identificados permiten tener en cuenta el lado por donde se realiza el agujero. Por ello, en la discretización 2 también se ha indicado la secuencia seguida en cada operación.
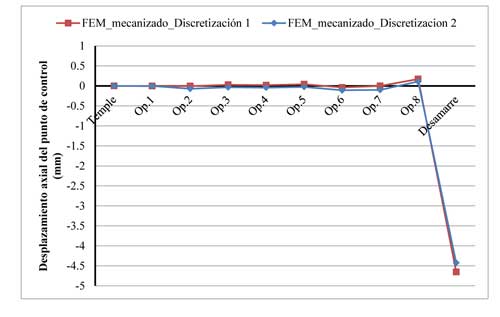
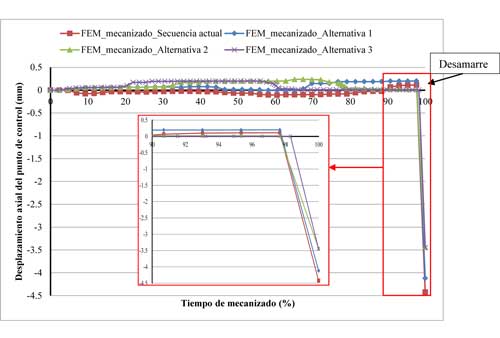
Para ver el efecto de la discretización, se ha tomado como referencia el desplazamiento axial del punto de control identificado en la figura 7. En la gráfica 1 se puede apreciar su efecto. No hay demasiada diferencia entre las dos opciones excepto para el último paso del desamarre. En el desamarre de la pieza se da la recuperación elástica del material. Se ve que debido a la discretización, la redistribución de las tensiones no es exactamente la misma y de ahí que las distorsiones finales sean un poco más grandes para el caso de la discretización basta. No obstante, la dicretización basta se puede considerar como una buena aproximación.
En la figura 8b se puede apreciar la sección deformada al final del mecanizado y en la figura 9a la redistribución de las tensiones axiales que se ha dado por el proceso de mecanizado para el modelo correspondiente a la discretización 2.
1.3.2. Alternativas a la secuencia actual de mecanizado
Una vez cuantificado la distorsión que se da en el proceso actual, el siguiente paso ha sido plantear diferentes alternativas de secuencias de mecanizado con el objetivo de disminuir la distorsión del punto de control.
Teniendo en cuenta las limitaciones y requerimientos específicos, se han analizado tres diferentes alternativas. Cada alternativa se describe en la figura 10. En cada una de ellas, el volumen de material eliminado en cada paso se ha identificado con dos números indicados en la sección de cada volumen. El primero hace referencia a cada operación y el segundo a la secuencia que se sigue.
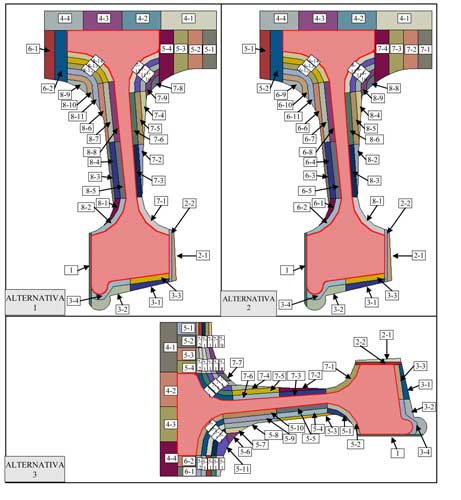
La discretización de las alternativas 1 y 2 son idénticas a la discretización 2 realizado en el anterior punto. En la alternativa 1 cambia el orden de las operaciones básicas descritas anteriormente y en la alternativa 2 cambia el orden de mecanizado de las caras del cubo y del disco respecto a la alternativa 1. Por último, en la alternativa 3 cambia un poco la discretización y también el orden de las operaciones de mecanizado en el cubo y el disco.
Al igual que en el punto anterior, la comparación de las tres alternativas se ha realizado en base a la deformación axial del punto de control. Esta comparación se puede ver en la gráfica 2. También se ha graficado la deformación de la secuencia actual para tener como referencia. Tal y como se aprecia, el efecto de la secuencia es notable en la distorsión que sufre el punto de control al final del proceso. Mediante la alternativa 1 se consigue disminuir la deformada final un poco pero con las alternativas 2 y 3 la disminución es más acusada (1 mm). Esto se debe sobre todo porque el mecanizado de la cara interior del disco se hace antes que la de la cara exterior y también porque ambas operaciones se hacen desde fuera hacia dentro, es decir, desde el lado de la zona de rodadura al eje de la rueda. Por tanto, se puede decir que estas dos operaciones son las más críticas para las distorsiones finales.
La diferencia de la deformada de las diferentes alternativas se puede ver en la figura 11.
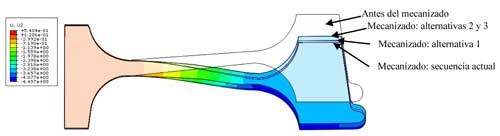
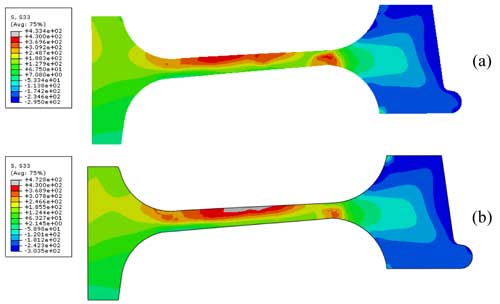
Aparte de las distorsiones finales, otro aspecto a considerar es el estado de tensiones residuales final que hay después del mecanizado. Como se observa en la figura 12, en las alternativas 2 y 3 además de conseguir que las distorsiones finales sean menores, se consigue también que las tensiones residuales sean menores.
2. Conclusiones
Mediante este trabajo se ha verificado que es factible realizar la simulación de las distorsiones finales de una cadena de procesos de fabricación de una manera relativamente simplificada.
Principalmente se ha analizado el proceso de mecanizado partiendo de un estado tensional inducido prácticamente por el proceso de temple. De esta manera, se ha estudiado el efecto que tiene el mecanizado en las distorsiones finales y también se ha demostrado que se puede disminuir ese efecto adverso jugando con las secuencias de mecanizado. Además, se han identificado las operaciones más críticas que tienen mayor impacto en la distorsión final. Concretamente, se ha visto que es recomendable mecanizar antes la cara interior del disco que la cara exterior y en ambos casos la eliminación del material debería de hacerse desde la zona de rodadura hacia el eje de la rueda.
Con todo eso, se ha verificado que la metodología simplificada utilizada para simular el proceso de mecanizado es válida para el propósito de este estudio, no siendo necesario utilizar modelos detallistas y computacionalmente costosos.
3. Referencias
[1] J. K. Rai y P. Xirouchakis, ‘Finite element method based machining simulation environment for analyzing part errors induced during milling of thin-walled components’, International Journal Of Machine Tools & Manufacture, 48, 629-643, 2007.
[2] T. Berruti y G. Ubertalli, ‘Influence of Cutting Parameters on Residual Stresses Induced by Milling in Pressure Die-Cast Aluminum Alloy Components’, J. Manu. Sci. Eng., vol. 123(4), pp. 547-551, 2001.
[3] P. Chevrier, B. Bolle, A. Tildu, P. Cezard y J. Tinnes, ‘Investigation of Surface Integrity in Highspeed End Milling of a Low Alloyed Steel’, vol. 43, nº 11, p. 113, 2003.
[4] M. San Sebastian, P. Alvarez y A. Echeverría, ‘New methodology applied to modelling machining distortion caused by stress relief’, CIRP Conference 2009, 2009.
[5] DEFORM, ‘Computer simulationof the Machinig Process’, 2002.
[6] D. Systemes, Abaqus Analysis User's Manual 6.12, 2012.
[7] T. D. Marusich, S. Usui, S. Lankalapalli y N. Saini, ‘Residual Stress Prediction for Part Distortion Modeling’, 2006.
[8] V. Dattoma, M. De Giorgi y R. Nobile, ‘On the evolution of welding residual stress after milling and cutting machining’, 2006.
[9] K. Jacobus, R. DeVor y S. Kapoor, ‘Experimenting on the residual stresses generated by endmilling’, Journal of Menufacturing Science and Engineering, vol. 123, nº 4, pp. 748-753, 2001.