Técnicas avanzadas de caracterización de material para optimizar el diseño de máquina de aplanado de chapa vía simulación numérica
En este artículo se presentan los resultados obtenidos de ensayos de tracción compresión para un acero de alta resistencia y se observa como los modelos de endurecimiento cinemático son válidos y necesarios para la modelización de este proceso.
1. Introducción
La competitividad y especificaciones requeridas por los consumidores en el mercado durante los últimos años, han impulsado al desarrollo de nuevos materiales y procesos de fabricación que aporten mejoras en lo que se refiere a sostenibilidad medioambiental, seguridad y precio. En este contexto, se ha prestado especial atención a los aceros de alta resistencia (HSS y AHSS), por su reducido peso y elevada resistencia.
El interés por estos materiales ha sido principalmente relevante en la industria automovilística, donde las restricciones medioambientales y económicas impuestas en los últimos años han promovido el desarrollo de automóviles ligeros, lo cual está ligado directamente con la reducción del consumo de combustibles y la reducción de la generación de CO2 [1-3]. Sin embargo, todavía hoy existe cierta incertidumbre en cuanto al comportamiento de estos materiales y cómo deben adaptarse a los procesos de fabricación. El uso de los aceros de alta resistencia supone un nuevo desafío para los fabricantes ya que muestran una conformabilidad limitada, una fuerte influencia del springback y se requieren grandes fuerzas para procesarlos debido a su alta resistencia [4,5].
Durante el proceso de fabricación de chapa, éstas son sometidas a laminación en frío y en caliente, lo que aporta unas propiedades mecánicas al material. Sin embargo, durante este proceso, la chapa adopta defectos de forma y en su interior se generan elevados niveles de tensiones residuales que hacen que la calidad de la chapa no sea la adecuada. Estos efectos se ven incrementados en el curso del bobinado, donde la chapa tiende a adoptar la forma de la bobina. Por todo esto, las tolerancias de planitud y especificaciones del material demandadas por el mercado no pueden ser alcanzadas mediante el proceso de laminado únicamente. Una corrección de estos defectos de chapa y la liberación de tensiones residuales en el interior del material es necesaria.
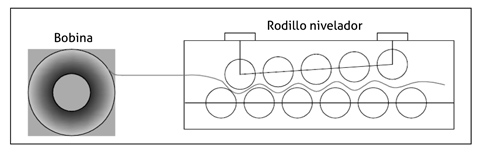
Existen distintas tecnologías de aplanado para eliminar los defectos de chapa y reducir tensiones residuales, sin embargo el aplanado por rodillos es el más habitual. En este proceso, la chapa es doblada en direcciones alternativas por un cierto número de rodillos con un gap variable entre la fila superior e inferior como se muestra en la Figura 1. El material está sujeto a deformaciones elastoplásticas con el objetivo de eliminar las tensiones residuales y homogeneizar aquellas que no pueden ser eliminadas. Hay muchos procesos que se pueden ver afectados si las chapas no han sido aplanadas adecuadamente debido a la existencia de las tensiones internas y defectos de forma, como por ejemplo procesos de prensado y estampación, procesos de corte, perfilado, etc. [6-7].
La teoría de plasticidad establece que en procesos en los que un material es sometido a cargas cíclicas de tracción-compresión, una vez que dicho material alcanza su límite elástico inicial, la curva de tracción-compresión cambia en los sucesivos ciclos. Es lo que se denomina ciclos de histéresis. Los ciclos de histéresis son específicos para cada material y van cambiando en cada ciclo, por lo que el límite elástico también. Dada esta situación, en la que la chapa modifica su comportamiento en cada rodillo por estar variando su curva de histéresis, resulta interesante profundizar en el estudio del comportamiento de material cuando se ve sometido a este tipo de cargas [9].
En concreto, en este trabajo se va a estudiar el comportamiento de un acero de alta resistencia, el TRIP700. Para ello, el modelo mixto isotrópico-cinemático de material desarrollado por Chaboche y Lemaitre (1990) [10-12] ha sido seleccionado para predecir el comportamiento de este material, por su capacidad para predecir la mayoría de los fenómenos característicos de los procesos de plasticidad cíclica, como el efecto Bauschinger, y por estar implementado en la mayoría de los códigos de elementos finitos. En primer lugar, se presenta una breve explicación sobre los defectos de chapa típicos y el fenómeno de aplanado por rodillos. A continuación, se describe el modelo de material seleccionado para definir el comportamiento del material. Después, se muestra la caracterización de los materiales, que se ha llevado a cabo mediante ensayos cíclicos de tracción-compresión, y el posterior ajuste del modelo a los datos experimentales obtenidos en los ensayos. En la siguiente sección se presenta el modelo de elementos finitos desarrollado para simular el proceso de aplanado por rodillos. En el último apartado de resultados, se comparan las diferentes simulaciones realizadas con el modelo mixto de material obtenido en la sección previa y un modelo isotrópico puro.
2. Aplanado por rodillos
2.1. Defectos de chapa
Los defectos de chapa ocurren debido a la existencia de tensiones residuales dentro del material. Estas tensiones aparecen por diferentes motivos como por ejemplo, un enfriamiento no homogéneo en el proceso de laminado, presión no uniforme en los rodillos del laminado, proceso de bobinado, impurezas en el material, etc. Durante el proceso de laminado, las tensiones aplicadas con los rodillos de trabajo inducen tensiones plásticas heterogéneas en la anchura y espesor de la chapa. Esto genera distintos tipos de defectos que se muestran en la Figura 2. Las bolsas laterales y ondas centrales son causadas por tensiones longitudinales a lo largo de la chapa. Una diferencia de longitud entre las fibras longitudinales de los extremos y de la parte central provoca este tipo de defectos. Las tensiones residuales transversales generan una diferencia en la longitud de fibras a lo largo del espesor. Esto provoca que una de las caras de la banda se encuentre en un estado de tracción y la otra de compresión.
Debido a la no homogeneidad del perfil de tensiones a lo largo del espesor, la chapa tiende a curvase tras el corte debido al momento desarrollado por esta distribución que no es simétrica respecto a la fibra neutra [13-15].
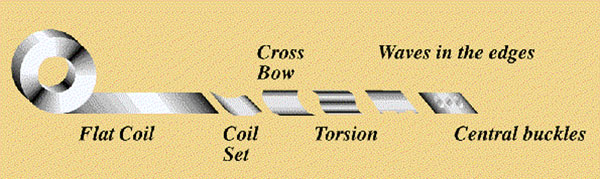
Figura 2: Defectos típicos de chapa.
No existe una deformación mínima impuesta a la que la chapa debe someterse durante el aplanado para que los defectos sean eliminados. Sin embargo, en bibliografía se pueden encontrar algunas recomendaciones según el tipo de defecto [13]. Para eliminar los defectos provocados por la forma de la bobina será suficiente con alcanzar 2 veces la deformación del límite elástico. Esta operación podría realizarse con una simple enderezadora. Para eliminar los otros defectos provocados por las diferencias entre tensiones internas en el interior del material como bolsas, ondas, arrugas, etc., la chapa debe ser deformada hasta 4 ó 5 veces la deformación del límite elástico. Se necesita una máquina de aplanar robusta para alcanzar estos niveles de deformación, por ello la máquina aplanadora por rodillos es utilizada para este fin.
2.2. Qué es aplanar por rodillos
Una máquina aplanadora de rodillos está formada por dos líneas de rodillos. La línea superior está diseñada con una inclinación que provoca que la deformación inducida por los primeros rodillos sea elevada y que esta vaya decreciendo a medida que se avanza hacia los últimos rodillos. Esta configuración de los rodillos proporciona mejores resultados en la calidad de aplanado final que la obtenida con una configuración de rodillos paralelos [16]. La chapa pasa a través de los rodillos y se dobla alternativamente provocando que las fibras de la superficie estén sometidas a esfuerzos de tracción y compresión. El proceso de aplanado consiste en una elongación plástica de chapa con el objetivo de unificar las longitudes de todas las fibras longitudinales y transversales, para que las tensiones internas sean minimizadas y homogéneas (Figura 3) [17].
Existe una controversia acerca de cuáles deben ser los parámetros que definan las condiciones óptimas para las que se considera que una chapa presenta una buena calidad de aplanado. Tradicionalmente en la industria se establece como criterio para obtener una buena calidad de aplanado, que al menos entre un 70-80 % del espesor de la chapa haya plastificado [18,19]. Normalmente este máximo de plastificación se alcanza entre el 3º y 4º rodillo y luego se va reduciendo hasta que en la salida la chapa se encuentra totalmente en rango elástico. Sin embargo, hay autores que analizan el nivel de tensiones residuales a la salida o la curvatura de la chapa como parámetros más indicativos de la calidad de aplanado [14].
2.3. Cómo se aplana
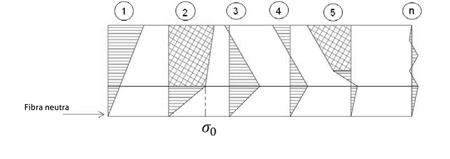
Para analizar el proceso de aplanado, es necesario entender que ocurre en el interior de la aplanadora. ¿Por qué una chapa entra en los rodillos con defectos y sale sin ellos? El proceso de aplanado puede dividirse en dos partes, la primera se corresponde con lo que sucede en los primeros rodillos de la aplanadora, y la segunda parte se corresponde con lo que ocurre en el resto de rodillos. En la primera parte, la penetración que ejercen los rodillos, y por lo tanto la deformación que sufre la chapa es mayor. En esta sección la chapa desarrolla zonas de deformación plástica que se va incrementando a medida que se dobla entre los rodillos, hasta llegar a un máximo de espesor plastificado, que suele alcanzarse en el 3º y 5º rodillo. La finalidad de esta primera sección de grandes deformaciones es que la mayor parte de las fibras del espesor alcancen el límite elástico y por lo tanto queden plastificadas, mientras que la zona central, cercana a la fibra neutra, permanecen en región elástica.
De esta forma, se consigue suprimir el gradiente de tensión en el ancho de la chapa, generando un nuevo perfil de tensiones en el espesor. Después de la primera parte, la penetración ejercida sobre la chapa va disminuyendo hasta que en la salida, los rodillos apenas la deforman [20]. La finalidad de la segunda parte es la de eliminar gradualmente la curvatura de la chapa y reducir el gradiente de tensiones generado en la primera sección a lo largo del espesor, para obtener a la salida una chapa en la que todo el espesor no esté plastificado (Figura 4) y con un reducido y homogéneo perfil de tensiones residuales.
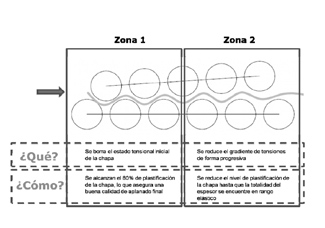
Si se selecciona una fibra de la chapa y se analiza su comportamiento en todo el proceso, está se verá sometida a ciclos de tracción compresión, tantos como parejas de rodillos haya en la máquina. Según la teoría de plasticidad, debido a los cambios microestructurales durante los procesos de cargas cíclicas, las propiedades físicas y la respuesta de tensión en el material se van modificando. En particular, los aceros sufren un endurecimiento cíclico o aumento de la resistencia a la deformación cuando son sometidos a cargas cíclicas. La intensidad con la que el material endurece en cada ciclo se reduce a medida que aumenta el número de ciclos hasta alcanzar un valor de saturación [11].
2.4. Variables de influencia
Hay diferentes factores involucrados en el proceso de aplanado, y de ellos depende el resultado final del aplanado de la chapa. Por ello es importante desarrollar una herramienta de cálculo, como es un modelo de elementos finitos, que permite analizar cómo estas variables influyen en la calidad de aplanado y así poder optimizar el diseño de máquina sin necesidad de realizar un gran número de ensayos experimentales. Los principales factores implicados en el proceso son el diámetro de los rodillos, la distancia entre rodillos, el número de rodillos, el tipo de material, el espesor de la chapa y la curvatura inicial que tiene la chapa [7,13,19-21].
Un rendimiento óptimo de la máquina aplanadora que se diseñe teniendo en cuenta todos estos factores, debe asegurar [18]:
- Alcanzar un porcentaje de plastificación en el espesor suficiente para eliminar los defectos (generalmente estimado en 80%)
- Las tensiones residuales a la salida deben ser mínimas
- No se debe exceder la fuerza máxima ni momento admisible por la máquina
3. Modelo de material
Durante el proceso de aplanado, el material se ve sometido a deformaciones elastoplásticas cíclicas, por ello, es necesario el desarrollo de ecuaciones constitutivas que describan el comportamiento de material bajo deformaciones plásticas cíclicas. La correcta descripción del comportamiento plástico de un material viene dado por la definición de un criterio de fluencia, una regla de flujo asociada y una ley de endurecimiento. En primer lugar, el criterio de fluencia indicará el punto en el que comienza la región plástica. El criterio de fluencia de von Mises es ampliamente usado para plasticidad cíclica y está implementado en la mayoría de los códigos de elementos finitos. El criterio para el caso uniaxial se define como:
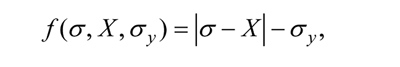
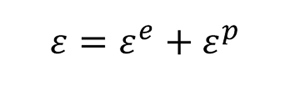
La parte elástica de la deformación se describe mediante la ley de Hooke. A su vez, la deformación plática sigue una regla de fluencia que expresa la relación entre los componentes de tensión y deformación de la siguiente forma:
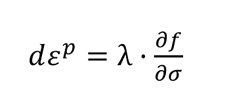
donde λ es el multiplicador plástico no negativo que debe satisfacer la condición de consistencia λ•f=0 (4).
Cuando la chapa metálica es sometida a ciclos de tracción compresión durante su paso a través de los rodillos, según la teoría de plasticidad, la chapa sufrirá cambios microestructurales que hacen que las propiedades físicas y la respuesta de tensión en el material se vayan modificando. En particular, los aceros pueden sufrir un endurecimiento o ablandamiento cíclico cuando son sometidos a cargas cíclicas. La intensidad con la que el material endurece o ablanda en cada ciclo se reduce a medida que aumenta el número de ciclos hasta alcanzar un valor de saturación. Por ello, es necesario definir el comportamiento de endurecimiento del material una vez que este ha plastificado. Existen dos tipos de endurecimiento, el endurecimiento isotrópico y el endurecimiento cinemático.
Sin embargo, los modelos de material mixtos que combinan una ley isotrópica con una ley cinemática han recibido una especial atención debido a la capacidad de mejora que ofrecen en la predicción del efecto Bauschinger y del comportamiento cíclico de material. En la Figura 5 se muestra el significado de este tipo de endurecimiento.
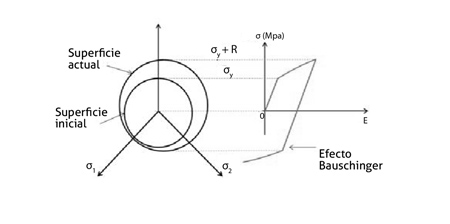
Uno de los más populares es el modelo de Chaboche y Lemaitre (1990). Este modelo combina la ley de endurecimiento isotrópica desarrollada por Voce, mediante la introducción del parámetro isotrópico R:
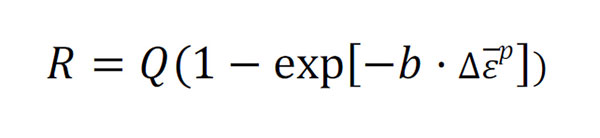
donde Q y b son parámetros de material y es la deformación plástica acumulada. Y la ley cinemática es introducida mediante la ley cinemática de Chaboche que define la evolución del backstress X a través de la siguiente expresión.
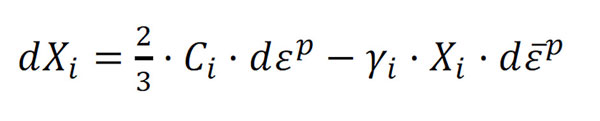
donde C y γ son parámetros de material y X representa el backstress.
4. Procedimiento experimental
Como ya se ha mencionado anteriormente, los modelos numéricos son una herramienta muy potente para el dimensionamiento de instalaciones de aplanado. En el presente trabajo se ha desarrollado un modelo numérico capaz de dimensionar estas instalaciones teniendo en cuenta el comportamiento real del material durante el proceso de aplanado. A continuación se exponen los pasos que hay que realizar, tomando como ejemplo el dimensionamiento de una instalación de aplanado para un acero de alto límite elástico, TRIP700, con 1,5 milímetros de espesor:
- Caracterización del material mediante un ensayo cíclico de tracción-compresión.
- Determinación de los parámetros óptimos del modelo de Chaboche y Lemaitre, mediante el ajuste del modelo a los datos experimentales.
- Desarrollo de un modelo de elementos finitos capaz de simular el proceso de aplanado.
- Introducción del modelo de material hallado en el modelo de elementos finitos desarrollado, para la obtención de resultados numéricos sobre el estado tensional y de deformaciones en la chapa a lo largo del proceso y a la salida; así como valores de esfuerzos y momentos necesarios en los rodillos para llevar a cabo el proceso.
4.1. Caracterización del material
En el presente trabajo el acero de alta resistencia TRIP700 ha sido investigado con el objetivo de analizar su modelado en el proceso de aplanado pro rodillos. El espesor de las muestras ha sido de 1,5 milíemtros y a continuación se presenta en la Tabla 1 las propiedades mecánicas de cada material.

El ensayo cíclico de tensión-compresión ha sido llevado a cabo para realizar la caracterización del endurecimiento del material. El equipo MTS Material Test System ha sido empleado durante la realización de los experimentos. Los datos de fuerza son adquiridos mediante una célula de carga axial de la máquina y los valores de deformación son medidos mediante galgas de pequeñas deformaciones para obtener una medición continua. El ensayo de tensión-compresión es sencillo y presenta la ventaja de que se obtienen valores de tensión-deformación directamente, sin necesidad de realizar análisis inverso. Sin embargo, existe una dificultad añadida ya que la probeta tiende a pandear cuando es sometida a compresión. Por ello se ha diseñado un utillaje para evitar el pandeo de la probeta durante el ensayo. La Figura 6 muestra el equipo experimental usado. La probeta ha sido sujetada entre dos placas dejando un gap de 0,1 milímetros y ha sido lubricada con Rhenus Fe 1300 para eliminar la influencia de la fricción durante el ensayo. Una de las placas tiene una ventana donde la galga es colocada tal como muestra la figura.

Durante el ensayo, la probeta ha sido sometida a 1 ciclo completo, en los que se ha deformado 2 % a tracción y -2 % a compresión.
4.2. Identificación de los parámetros del modelo de Chaboche y Lemaitre (1990)
La identificación de los parámetros del modelo ha sido realizada mediante la minimización de una función objetivo, definida como la diferencia entre el valor predicho por el modelo y los datos experimentales.
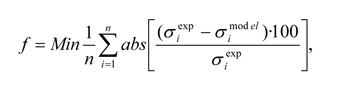
Donde n es el número de datos experimentales, σiexp es la tensión obtenida en el ensayo experimental, y σimodel es la tensión predicha por el modelo.
4.3. Modelo de elementos finitos del proceso de aplanado
Gracias al desarrollo de un modelo de elementos finitos que simule el proceso de aplanado por rodillos, se puede tener información de la deformación progresiva que sufre la chapa desde el inicio al final del aplanado, siendo una herramienta necesaria para un buen diseño y asegurar el adecuado aplanado final de la banda metálica.
El modelo numérico ha sido creado con Marc Software, por su experiencia en procesos de conformado de chapa para analizar contactos y grandes deformaciones.
Además, se ha estimado un tiempo de cálculo menor con este programa que con otros programas comerciales de elementos finitos. La aplanadora desarrollada en el modelo está compuesta con 13 rodillos con una penetración inicial de -1.125 milímetros y una penetración final de 1.433 milímetros. Un coeficiente de fricción de 0,25 ha sido establecido para el proceso. La chapa ha sido discretizada usando elementos de 4 puntos de integración y el mayado empleado ha sido desarrollado con una distribución no uniforme a lo largo de la chapa. En concreto, un mayado más fino con 16 elementos en el espesor ha sido usada en la zona central para obtener resultados más precisos y estabilizados, mientras que un mayado más basto ha sido usado en el resto de la chapa para reducir el tiempo de cálculo.
El modelo ha sido creado con 2 rodillos de tiro que están situados justo antes de la máquina para que estos ayuden a la chapa a moverse hacia la aplanadora. La figura 7 muestra una esquema del modelo 2D desarrollado en la zona de los rodillos de trabajo y las especificaciones geométricas se detallan en la tabla 2.
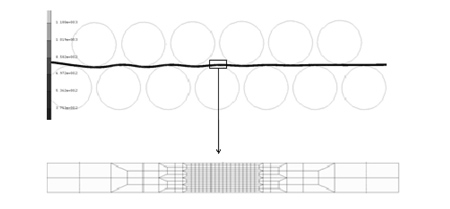

5. Resultados
En esta sección se presentan los resultados experimentales de los ensayos de tracción-compresión, así como la respuesta numérica del modelo con una combinación óptima de parámetros.
5.1. Modelo del material
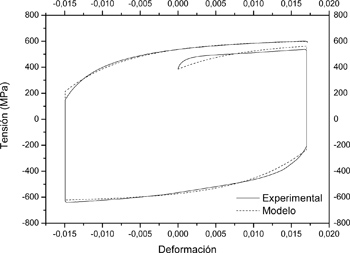
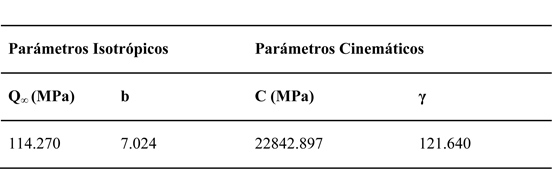
El modelo mixto de Chaboche y Lemaitre desarrollado en la sección 3, ha sido ajustado a las curvas obtenidas durante el ensayo de tracción-compresión mediante un método de optimización. En la Figura 8 se grafica el resultado del ajuste de los parámetros del modelo a los datos experimentales de un ensayo de 1 ciclo, y en la Tabla 3 se detallan los parámetros obtenidos en la optimización.
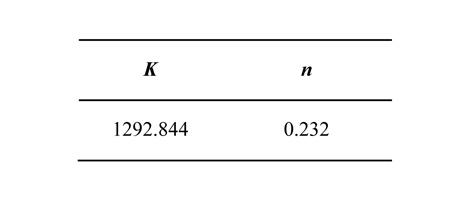
En los resultados numéricos obtenidos de las simulaciones, se ha comparado el modelo mixto hallado anteriormente con un modelo isotrópico puro, mediante una función con dos parámetros del tipo:
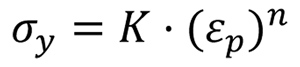
Donde K y n son parámetros del material. En la Tabla 4 se muestran los valores obtenidos de estos parámetros para el TRIP700.
5.2. Resultados numéricos del proceso de aplanado
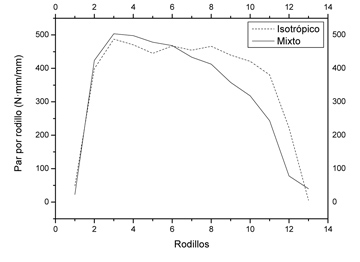
Los valores de los parámetros de material para ambos modelos, mixto e isotrópico, obtenidos en el apartado anterior han sido introducidos en el modelo de elementos finitos para simular el proceso de aplanado. En las Figuras 9, 10 y 11 se comparan los resultados de obtenidos cuando la simulación se ha realizado con un modelo isotrópico y uno mixto. Los valores dados de par y fuerza por rodillo mostrados son N•mm/mm y N/mm respectivamente. Esto se debe a que el modelo desarrollado es 2D, por lo tanto para obtener el valor total sería necesario multiplicar estos valores por el ancho de la chapa a aplanar.
Se observa en la Figura 9 que ambos modelos presentan la misma tendencia en cuanto al par necesario en cada rodillo para que la chapa pase entre ellos. Los valores alcanzados van a depender directamente del coeficiente de fricción impuesto en la simulación, que en este caso es de 0,2, valor establecido de forma empírica como el valor necesario para que la chapa fuera arrastrada por los rodillos. En ambos casos se alcanza el máximo en los primeros rodillos y luego cae rápidamente. Este hecho tiene sentido ya que según bibliografía y la propia experiencia de los fabricantes, parece que entre el 3º y 5º rodillo es donde se alcanzan mayores valores de deformación y plastificación de la chapa, por lo tanto el par requerido es mayor. Sin embargo, el uso de un modelo isotrópico en el modelado del proceso predice unos valores superiores de par respecto a los valores obtenidos con el modelo de mixto.
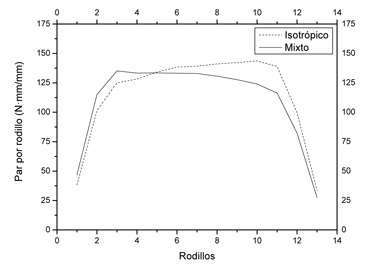
En la Figura 10 se presentan las reacciones verticales de los rodillos durante el proceso. Se aprecia una diferencia en cuanto al comportamiento seguido dependiendo el modelo de material con el que se ha realizado la simulación. El modelo isotrópico presenta un patrón creciente de fuerza en los rodillos hasta casi el final del proceso, mientras que el modelo mixto presenta de nuevo un máximo en el tercer rodillo, para ir después cayendo en los rodillos sucesivos.
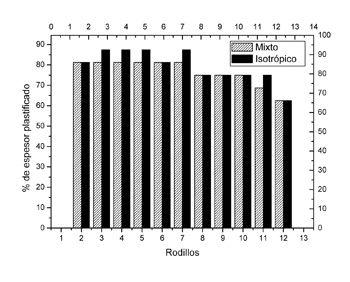
En la Figura 11, se muestra el porcentaje de plastificación alcanzado en cada rodillo. Esto hace referencia al porcentaje de espesor de la chapa que se encuentra plastificado en el paso por cada rodillo. En ambos casos se ha superado el 80% de espesor plastificado. Dicho valor se ha establecido como referente entre los principales fabricantes de aplanadoras, como el nivel de plastificación que asegura una planitud de chapa a la salida de alta calidad.
6. Conclusiones
En los últimos años ha habido un interés creciente por los aceros de alta resistencia debido a su elevada resistencia y reducido peso. Estas características los convierten atractivos principalmente en el sector automovilístico, donde la fabricación de coches seguros, ligeros y de bajo coste, se ha convertido en uno de los principales objetivos del sector.
Existe un importante desconocimiento acerca del comportamiento de estos materiales. Por ello, resulta de elevado interés realizar un estudio profundo de su comportamiento cuando son sometidos a procesos de aplanado, con el objetivo de optimizar el proceso y obtener chapas de elevada calidad para su posterior procesado. Por ese motivo, se ha seleccionado el modelo mixto de endurecimiento de Chaboche y Lemaitre para predecir el comportamiento del TRIP700 en lugar de un modelo isotrópico, por su capacidad para predecir el comportamiento de los aceros cuando son sometidos a esfuerzos cíclicos de tensión-compresión y por estar implementado en la mayoría de los códigos de elementos finitos. Este modelo ha sido capaz de representar algunos de los fenómenos más importantes que se dan en cargas cíclicas, como el efecto Bauschinger y el endurecimiento del material.
Para la determinación de los 4 parámetros de material definidos en el modelo de Chaboche y Lemaitre, el ensayo de tracción-compresión ha resultado ser una forma rápida y fácil de obtener datos experimentales, mediante la ayuda de un utillaje diseñado para evitar el pandeo de la probeta durante los ensayos.
En cuanto a los resultados numéricos obtenidos en las simulaciones, cabe destacar la sobreestimación realizada por el modelo isotrópico en términos de par y fuerza por rodillo. Estos resultados acarrean inconvenientes a la hora de realizar el diseño de la aplanadora, ya que el diseño dictado por un modelo isotrópico implica un mayor gasto en el desarrollo de una máquina de gran potencia, que según el modelo mixto no sería necesario. El porcentaje de plastificación alcanzado con la configuración de máquina establecida ha sido aceptable con ambos modelos por haber superado el 80% de plastificación del espesor en el 3º rodillo.
7. Líneas futuras
El proyecto desarrollado proporciona una herramienta plenamente funcional y útil para el análisis del proceso de aplanado. No obstante, existen todavía muchos campos de mejora sobre los que se está trabajando. Entre otros la validación del modelo de simulación numérica con un prototipo experimental de aplanado desarrollado por Fagor Arrasate. El desarrollo de este prototipo va a permitir conocer valores reales de fuerza y par en los rodillos, así como las deformaciones sufridas por la chapa durante el proceso de aplanado mediante la sensorización de esta. De forma paralela se está desarrollando un utillaje que permita determinar coeficientes de fricción entre un cuerpo plano (chapa) y un cuerpo curvo (rodillo), para así realizar el modelizado numérico con coeficientes de fricción reales.
Referencias
[1] B Engl, Cold Rolled HSLA Sheet and Strip Products, International symposium niobium, Niobium 2011, Orlando, Florida, USA, 2001, pp. 675.
[2] J Larrañaga, Geometrical accuracy improvement in flexible roll forming process by means of local heating, (2011).
[3] M Shi, X Zhu, C Xia, T Stoughton, Determination of nonlinear isotropic/kinematic hardening constitutive parameters for AHSS using tension and compression tests, (2008) 137-142.
[4] X Lemoine, L Durrenberger, H Zhu, R Kergen, Mixed hardening models: parameters identification on AHSS steels, Arcelor Mittal R&D.
[5] J Mendiguren, L Galdos, ES de Argandoña, E Silvestre. Ludwik’s Model Parameter Identification for V-Bending Simulations with Ti64 and MS1200, Key Eng Mat. 504 (2012) 889-894.
[6] E Doege, R Menz, S Huinink. Analysis of the levelling process based upon an analytic forming model, CIRP Ann.Manuf.Technol. 51 (2002) 191-194.
[7] E Theis. Strip shape control, Metalfomingmagazine. (2004).
[9] B Cox, Roller leveling 101, 2012 (2007).
[10] JL Chaboche. Constitutive equations for cyclic plasticity and cyclic viscoplasticity, Int.J.Plast. 5 (1989) 247-302.
[11] J Lemaitre, JL Chaboche, Mechanics of solid materials, Cambridge Univ Pr 1994.
[12] R Halama, J Sedlák, M Sofer, Phenomenological Modelling of Cyclic Plasticity, (2012).
[13] A.P. Design, Levelling in detail, 2012 (2009).
[14] K Park, S Hwang. Development of a finite element analysis program for roller leveling and application for removing blanking bow defects of thin steel sheet, ISIJ Int. 42 (2002) 990-999.
[15] L Bodini, O Ehrich, M Drauhausen, Heavy plate leveler improvement by coupling a model to a flatness gauge, 2012.
[16] L Cui, X Hu, X Liu, Analysis of leveling strategy for a plate mill, Advanced Materials Research. 145 (2011) 424-428.
[17] J ROBERTS, T SHEPPARD. Mechanics of Tension-Levelling Process, Journal of the Institute of Metals. 99 (1971) 293-&.
[18] J Bourgon. Levelling: modelling and industrial applications, La Revue de Métallurgie - CIT. (1993).
[19] L Yan, B Snider, Reducing seturp time in strip leveling, 2012 (2008).
[20] RP Smith. The Effect of the Number of Leveling Rolls on the Straightening Process, IRON AND STEEL TECHNOLOGY. 4 (2007) 57.
[21] L Madej, K Muszka, K Perzyński, J Majta, M Pietrzyk. Computer aided development of the levelling technology for flat products, CIRP Ann.Manuf.Technol. 60 (2011) 291-294.
Agradecimientos
El trabajo presentado en este artículo ha sido llevado a cabo gracias a la cooperación con FAGOR ARRASATE y KOONIKER, con la financiación del Programa Nacional INNPACTO para la cooperación público-privada (Ministerio Español de Ciencia e Innovación).