Caracterización de la distribución del agua en riego por aspersión estacionario
14 de julio de 2010
La distribución del agua de riego generada por un aspersor está influida por factores externos como la presión, el viento y el tamaño de las boquillas, y además, por factores que tienen que ver con el diseño interno del aspersor. Según Clemmens y Dedrick (1994), la eficiencia del riego por aspersión puede situarse entre el 70 y el 85% en el caso de coberturas totales, requiriéndose un valor mínimo de coeficiente de uniformidad (CU) del 80% para considerarse aceptable, siendo un reto actual y futuro, el uso eficiente del agua en las zonas donde ésta es un recurso escaso.
Se han realizado numerosos trabajos sobre la uniformidad de reparto de agua en riego por aspersión, pero suele haber desacuerdo en las conclusiones. La forma geométrica del espaciamiento suele ser uno de los aspectos con mayores discrepancias. Algunos trabajos recomiendan los marcos triangulares, mientras que otros indican que no existen ventajas significativas entre estos marcos y los rectangulares.
La velocidad del viento se incrementa con la altura según una función logarítmica, por lo que, en el diseño de los sistemas, el aspersor se suele colocar lo más bajo posible, según la altura de los cultivos a regar. Esta es otra razón por la que el ángulo de descarga de la mayor parte de los aspersores agrícolas es de 23º a 27º, en lugar de los 32º que sería el que consigue máximo alcance en condiciones sin viento. Sin embargo, experiencias con aspersores en riego en bloque ofrecen una mayor uniformidad de riego situando el aspersor a 2 metros del suelo, frente a una altura de 0,65 metros, debido a que a una mayor altura se producen curvas radiales con un mayor alcance mojado.
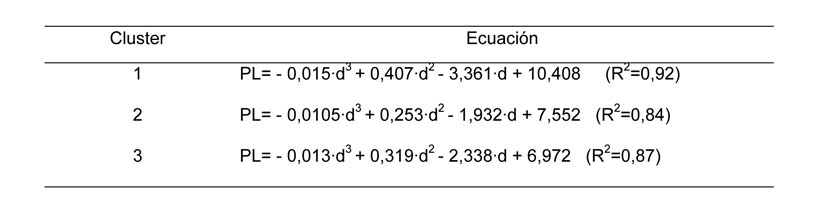
Wiersma realizó pruebas con diferentes combinaciones boquilla-presión-marco de riego, poniendo de manifiesto cómo la uniformidad decrecía linealmente con la velocidad del viento. Tarjuelo y col., comprobaron esta afirmación, poniendo de manifiesto que dicha relación se ajusta a un polinomio de segundo grado. Montero, basándose en ensayos de un aspersor al aire libre, comprobó que el mejor ajuste entre el CU y la velocidad del viento se consigue con ecuaciones polinómicas de 3º grado; esto es así, pues conforme aumenta el viento disminuye la uniformidad, pero al llegar a velocidades de viento altas la uniformidad decrece más lentamente (con una menor pendiente) manteniéndose casi constante.
Von Bernuth y Seginer comprobaron que la uniformidad de distribución (UD) decrece con el aumento de la velocidad del viento, y que la orientación del marco de riego respecto a la dirección del viento también influye sobre la UD.
El espaciamiento entre aspersores es uno de los aspectos fundamentales en el diseño del sistema. Heermann y Kohl indican, según recomendaciones de Strong, separaciones del 60% del diámetro efectivo del aspersor para marcos cuadrados o en triángulo y el 40% y 75% para marcos rectangulares, en condiciones de vientos poco intensos (menores de 2 m/s.).

En la bibliografía, existe unanimidad sobre la disminución del CU al aumentar la velocidad del viento en riego por aspersión estacionario. La deformación del modelo de distribución de agua de un aspersor por la acción del viento produce, además de un aumento del radio mojado a sotavento y una disminución a barlovento, que la rotura del chorro en gotas se produzca más cerca de la boquilla (sobre todo a barlovento), por la mayor diferencia de velocidad entre el chorro y el aire que lo circunda. Este último hecho acorta el camino recorrido por la gota desde la boquilla hasta el suelo al haberse formado antes, y justifica que el incremento del radio mojado a sotavento sea mayor que la disminución a barlovento (Montero, 1999).
Montero determinó una relación inversa entre la velocidad del viento y CU cuando el aspersor utiliza doble boquillas, para W>2 m s-1, mientras que con una sola boquilla la uniformidad se mantiene casi constante. Con el objetivo de caracterizar la distribución de agua con distintas combinaciones de aspersor, marco, boquillas y presión de trabajo, se planteó el presente trabajo.
Materiales y métodos
Siguiendo las normas Asae S.330.1 (1985), Asae S.398.1 (1985), ISO 7749-2 (1990) y UNE 68-072-86 (1986), las combinaciones ensayadas fueron: tres tipos de aspersores (Agros 35, Agros 40 y VYR 37), cuatro combinaciones de boquillas (4,4+2,4; 4,8+2,4; 4,8 y 5,2 mm) y tres presiones de trabajo (220, 320 y 450 kPa). A las curvas de distribución pluviométrica se les aplicó un análisis cluster para buscar sus posibles agrupamientos utilizando la metodología descrita por Salomon y Bezdek (1980) y Nin y col. (2007).
Los ensayos de riego en bloque al aire libre se realizaron en un área de 0,36 ha localizada en el campo de prácticas de la Escuela Técnica Superior de Ingenieros Agrónomos de Albacete. La instalación consta de cuatro laterales de tubería de aluminio (76 mm de diámetro), con cuatro aspersores por lateral (fig.1), dispuesto en dos tipos de marco: 15 x 15 m en cuadrado y 18 x 15 m en triángulo. La altura de los aspersores sobre la superficie del suelo es de 2,3 m. Una red de pluviómetros tronco cónico, casi cilíndrico, con un diámetro de recogida de 0,16 m y 0,15 m de altura, separados a 3 m x 3 m se colocaron entre los cuatro aspersores centrales. Se siguió la metodología propuesta de Merriam y Keller (1978) y Merriam y col. (1980), teniendo en cuenta, además, lo que establecen las normas UNE-68-072-86 (1986), ISO 7749-2 (1990) y Asae S330.1.
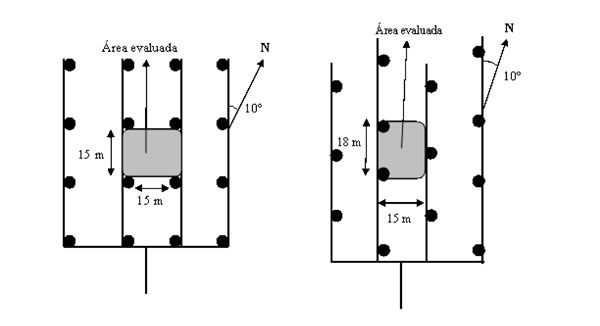
Las combinaciones aspersor-boquilla-presión antes descritas se evaluaron en dos marcos de riego y a tres rangos de velocidades de viento (0-2; 2-4 y mayor a 4 m s-1), realizando un total de 96 ensayos (Tabla 1).
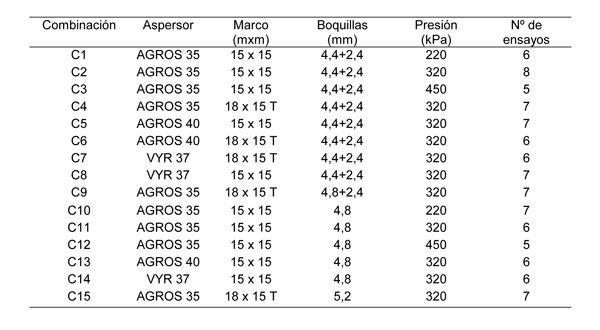
Los análisis estadísticos realizados fueron: análisis cluster de las curvas radiales, coeficiente de correlación de Pearson y el Modelo Lineal General, con el software Statistical Product and Service Solutions (SPSS), versión 14.0 de SPSS Inc. Headquarters.
Resultados y discusión: Ensayos radiales
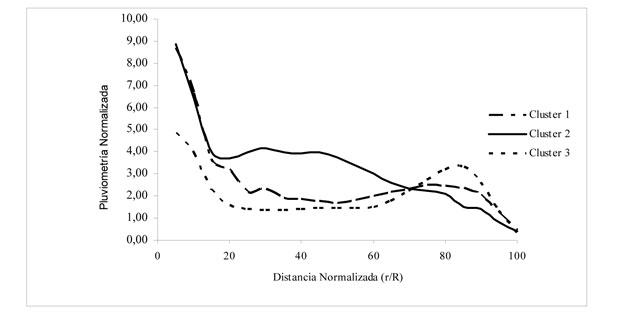
El análisis cluster identificó tres tipos de curvas radiales, que coincidió con los clásicos modelos elíptico, triangular y 'rosquilla', que están relacionados con el número de boquillas y el caudal descargado por el aspersor. El primer cluster está compuesto por aspersores con una o dos boquillas y caudal promedio de 1600 l h-1; el segundo cluster por aspersores con dos boquillas y descarga promedio de 1700 l h-1 y el cluster tres por aspersores con una sola boquilla y descarga promedio de 1500 l h-1 (Fig. 2).
Los mayores valores de los parámetros de uniformidad en condiciones sin viento en ambos marcos de riego, se obtienen con las curvas pluviométricas obtenidas en el cluster dos o curva radial tipo triangular, mientras que los peores en el cluster tres o curva radial tipo 'rosquilla' (Tabla 2).
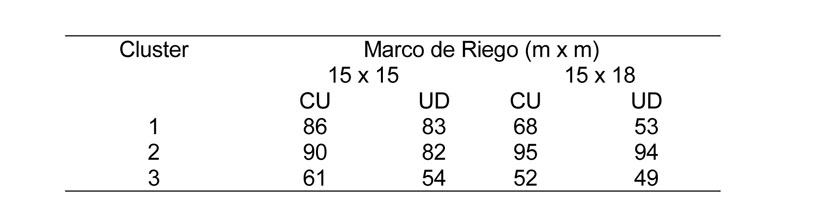
Ensayos al aire libre
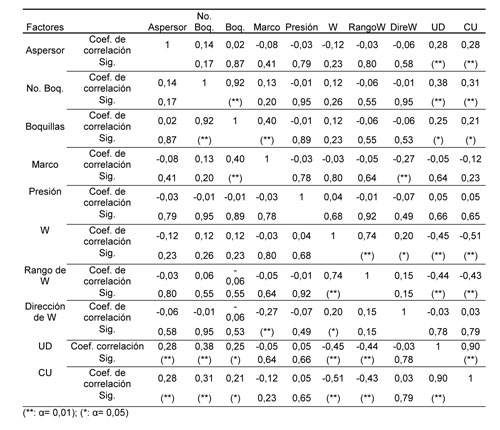
A los factores que intervienen en el riego por aspersión: aspersor, número y diámetro de boquillas, marco de riego, presión de trabajo y velocidad del viento, se les aplicó el análisis de correlación de Pearson. Se obtuvieron correlación significativa (α=0,01) de los parámetros de uniformidad UD y CU con los aspersores, el número de boquillas y la velocidad del viento; mientras que con el diámetro de boquillas la correlación es significativa con un α=0,05; también el marco de riego está correlacionado con la dirección del viento y el diámetro de las boquillas (Tabla 5).
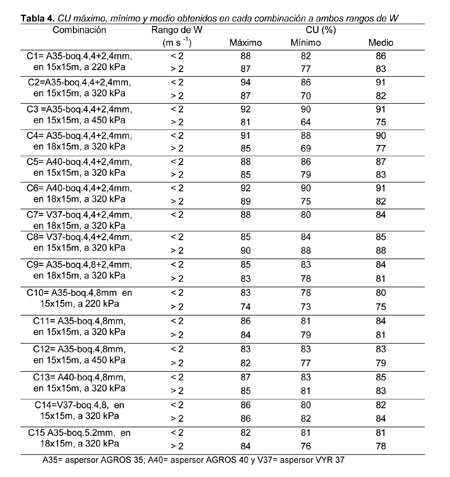
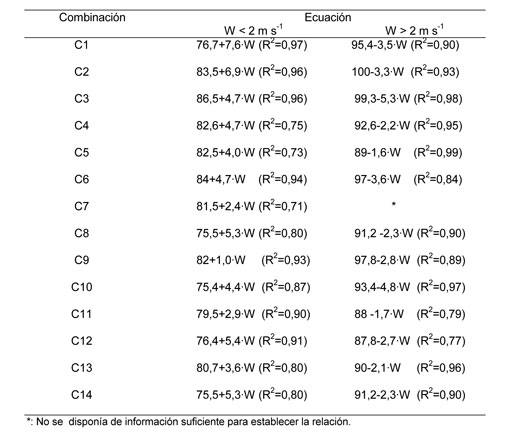
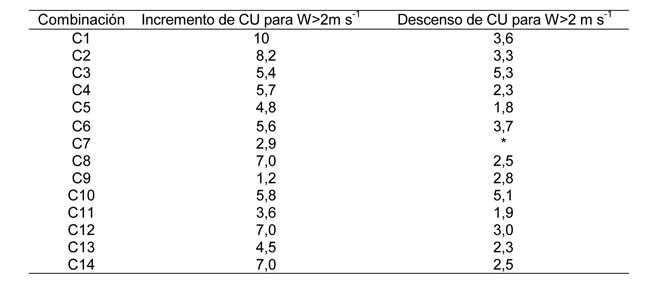
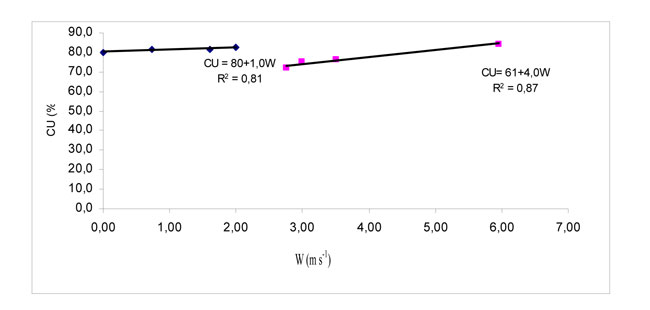
Al existir diferencias debido a la variable viento, se realizó una división de los CU en función de la velocidad del viento (W), para W menor y mayor a 2 m s-1, Dechmi y col. realizaron esta misma división, ya que determinaron que a partir de 2 m s-1 existe un descenso acusado de la uniformidad del riego. Al realizar esta división se encontró que existe una relación (CU-W) de tipo lineal. Wiersma realizó pruebas con diferentes combinaciones boquilla-presión-marco de riego, manifestando cómo la uniformidad decrecía linealmente con la velocidad del viento. Se observó que existe una relación lineal con pendiente positiva para W menores a 2 m s-1 y negativa para W mayores a 2 m s-1, en las combinaciones con boquillas 4,4+2,4; 4,8+2,4 y 4,8 mm (Tabla 7). Para W menores a 2 m s-1 se produce un aumento del CU a medida que W aumenta; mientras que a partir de 2 m s-1 es al contrario, a medida que aumenta el W disminuye el CU (Tabla 8).
Los mejores parámetros de uniformidad UD y CU (en ambos marco de riego) se obtienen con aspersores que tienen curvas radiales del tipo triangular
Las características del aspersor influyen sobre los CU y la UD. Con dos boquillas el Agros 35 se comporta mejor que los demás; mientras que con una boquilla el mejor es el Agros 40.
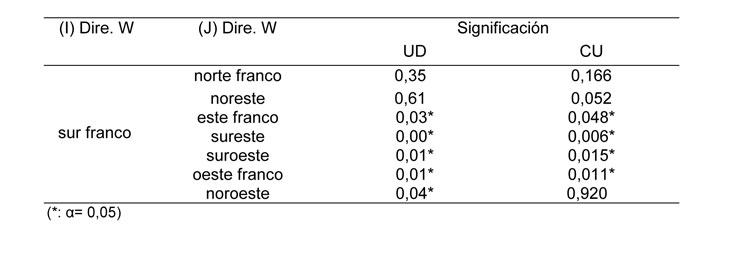
La orientación del marco con respecto a la dirección de los vientos predominantes tiene influencia en los parámetros de uniformidad. Con vientos paralelos al marco se obtienen mayores UD y CU.
Las velocidades de vientos bajas (hasta 2 m s-1) tienden a mejorar la uniformidad de aplicación del agua, mientras los valores superiores de viento tienden a disminuir la uniformidad, aunque esta disminución es mayor con dos boquillas que con una.
La boquilla 5,2 mm es la que mejor se comporta con velocidades de vientos altas (mayor a 2 m s-1).



















