Curvado en frío, cálculo y predimensionamiento
El proceso de curvado de un vidrio se puede realizar de varias formas. Hoy en día existen empresas que se dedican a esta transformación utilizando hornos de curvado-templado y hornos de curvado por moldeado o gravedad del vidrio. Cuando se calienta un vidrio, su elasticidad aumenta con la temperatura, lo que le permite adoptar una gran variedad de formas.
Este proceso de curvado en caliente consume mucha energía y precisa de una alta cualificación, lo que supone un alto coste en su producción.
Para reducir los costes del vidrio curvado en caliente, la ingeniería de construcción de envolventes ha desarrollado soluciones que evitar tener que calentar el vidrio, aplicando el curvado en frío ‘in situ’. Esta técnica de instalación permite que el vidrio pueda adoptar una forma curvada simple, evitando así el sobrecoste del curvado en caliente.
El vidrio es bastante elástico, incluso a temperatura ambiente. En la imagen se puede apreciar la curvatura que adquiere colocado en horizontal, sin tratamiento térmico previo alguno, bajo la única acción de su propio peso.

Diseño
Para diseñar un vidrio que va a ser curvado en frío in-situ, se requieren una serie de condiciones que se deberán estudiar previamente.
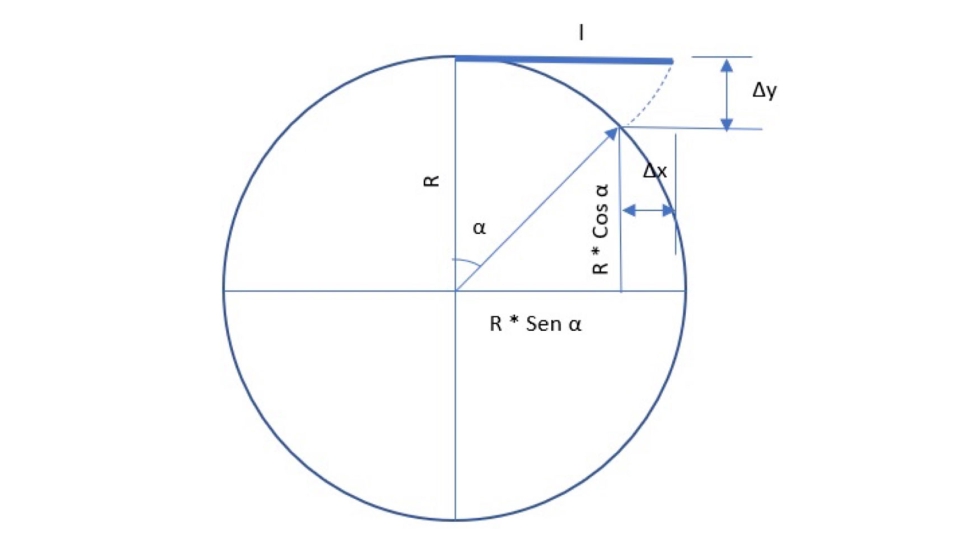
Como se puede ver en la figura, disponemos de un vidrio de longitud ‘l’, que una vez sometido a una carga o incluso por efecto su propio peso, va a adquirir una curvatura final que vendrá caracterizada por su radio de curvatura ‘R’. El extremo del vidrio que ha adoptado esta forma final se ha desplazado en los ejes x e y una cantidad Δx y Δy (ambas negativas), que no conocemos, pero que se pueden determinar a través de fórmulas trigonométricas básicas.
Sabemos que la longitud total de la circunferencia es,
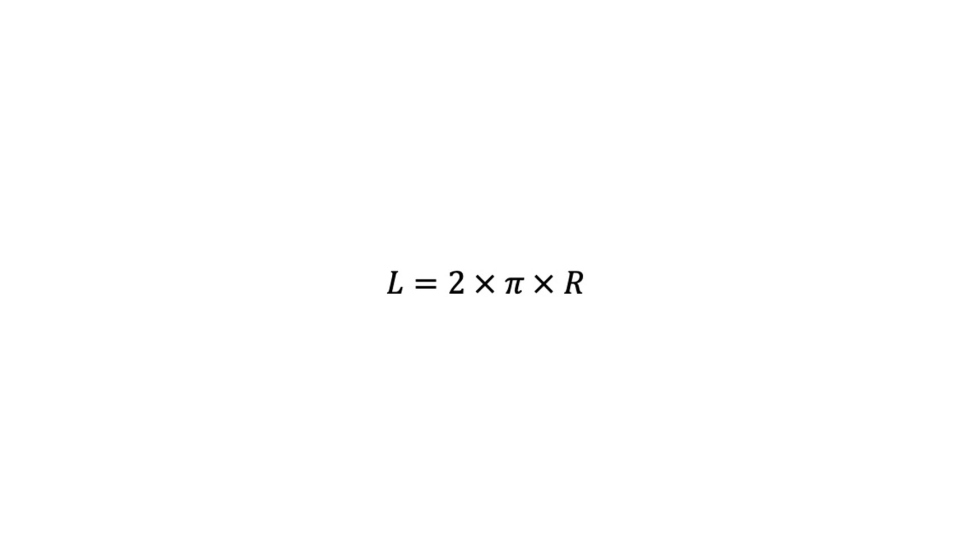
Mediante una regla de tres simple determinaremos el arco abarcado por el vidrio una vez que que adopte su forma final,
L → 360°
l → α
Donde,
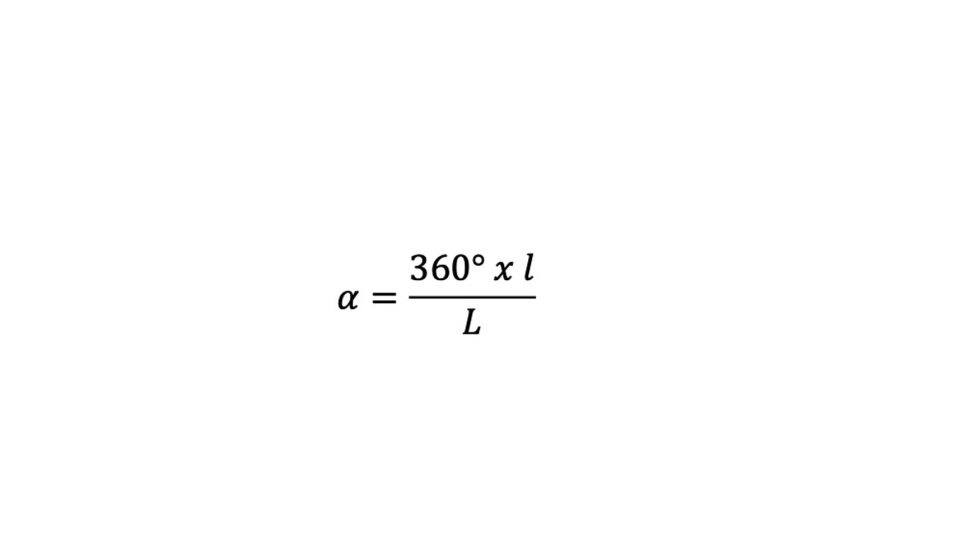
Una vez conocido el valor del ángulo α, se podrán determinar los desplazamientos del extremo del vidrio Δx y Δy con el siguiente razonamiento:
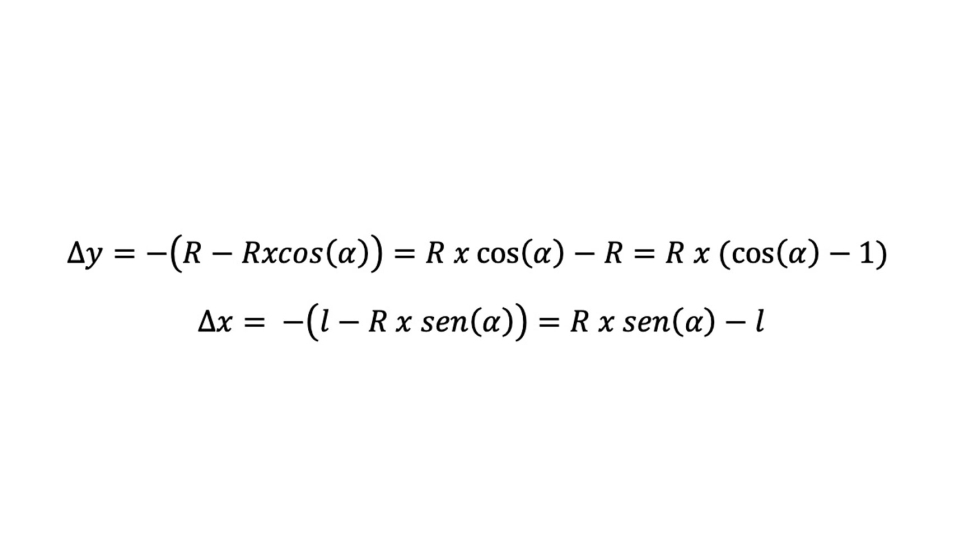
Utilizando estos valores podemos determinar las coordenadas cartesianas del extremo del vidrio siguiendo la curvatura de radio deseado, (este dato nos será de gran utilidad a la hora de determinar las coordenadas en las que posicionar el vidrio para las tensiones a las que queda sometido utilizando programas de cálculo mediante elementos finitos (ver anexo 1) y su parametrización en planos de soporte CAD.
Determinación de la tensión del vidrio una vez adoptada la forma deseada
A continuación vamos a aplicar las relaciones fundamentales de la flexión, considerando el vidrio como una viga sometida a flexión pura,
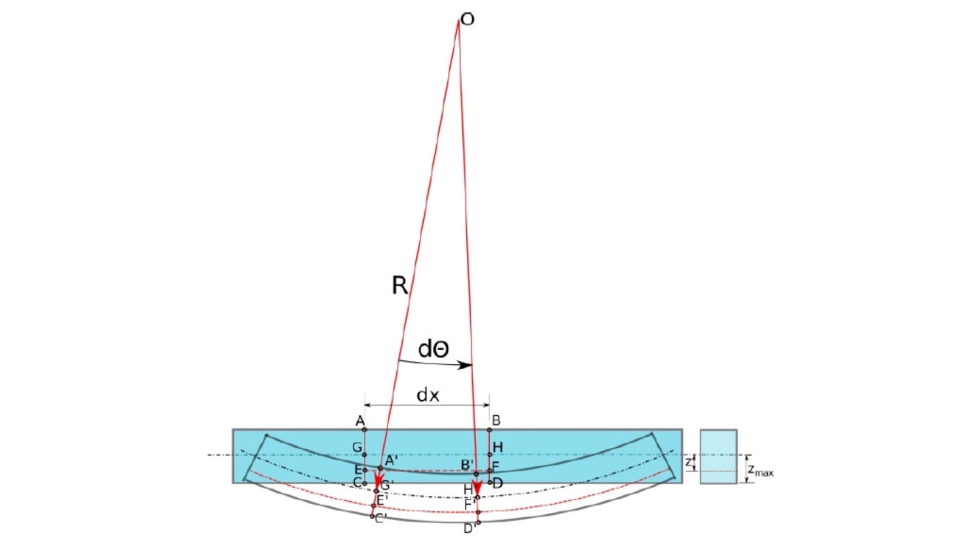
La imagen representa la deformada de una viga de sección cualquiera sometida a flexión pura. Ya que las fibras del material que deforman la superficie superior se acortan y la des la superficie inferior se alargan, debe existir un plano intermedio donde la deformación longitudinal sea nula. A este plano lo llamamos línea neutra y el eje longitudnal que pasa por este plano se llama Eje neutro.
Consideramos un elemento diferencial dx de viga entre las secciones indicadas AC y BD en el dibujo. Las fibras GH y EF son iguales ante la deformación, pero después de la deformación, la fibra EF se habrá alargado hasta E’F’ mientas que la fibra G’H’ coincidiendo con la línea neutra, quedará de la longitud original.
Por lo tanto R es el radio de curvatura de la fibra G’H’ y,
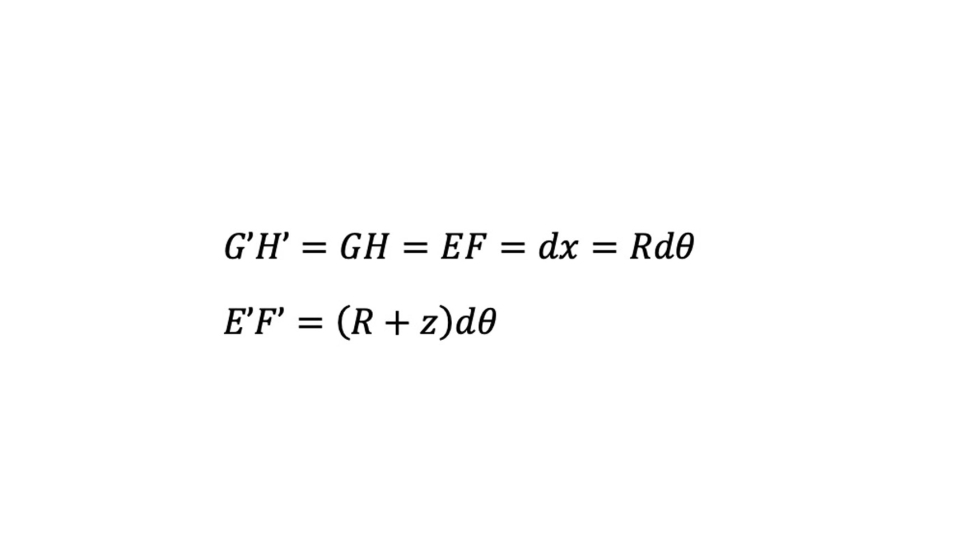
El alargamiento unitario de la fibra E’F’es,
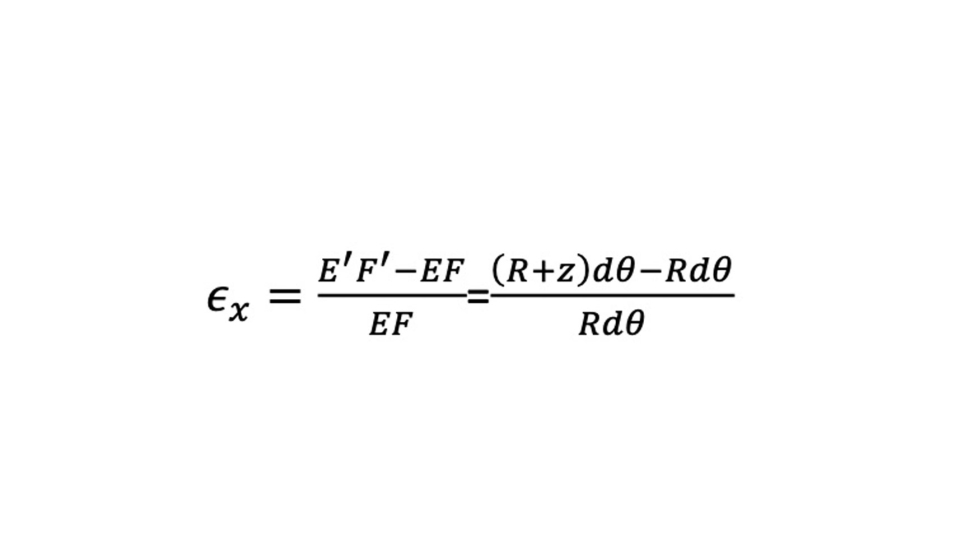
Obteniendo una relación fundamental,
?x=z/R
Y como,
R=dx/dθ
Tambien se puede expresar,
?x=z dθ/dx
De la ecuación
?x=z/R se desprende que el alargamiento unitario está distribuido linealmente a través de la sección, con los valores máximos en las superficies extremas y de valor nulo justo en el eje neutro.
Esta ecuación es totalmente independiente del tipo de material y de si su relación σ-? es lineal o no-lineal.
Si relacionamos esta ecuación con la ecuacion constitutiva procedente de la Ley de Hooke que relaciona σ y ? tal que,
σ=E?,
Donde E es el, módulo de elasticidad del material o módulo de Young (Thomas Young, 1773-1829) y es una propiedad específica de cada material.
Si relacionamos ambas ecuaciones
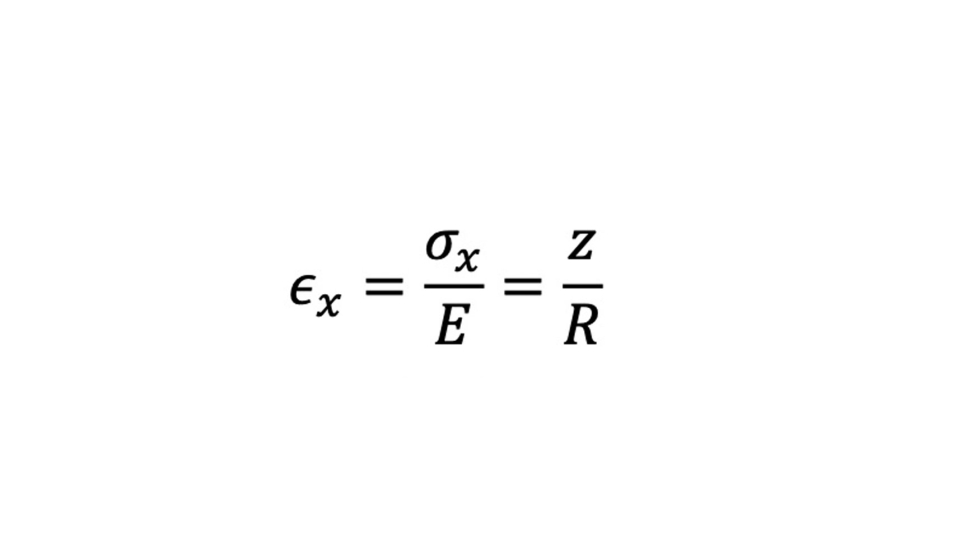
Por otro lado utilizando la relación entre σ y M donde existe una relación entre la tensión normal y el momento flector conforme a,
σ=M/I z
Obtendremos las relaciones fundamentales de la flexión,
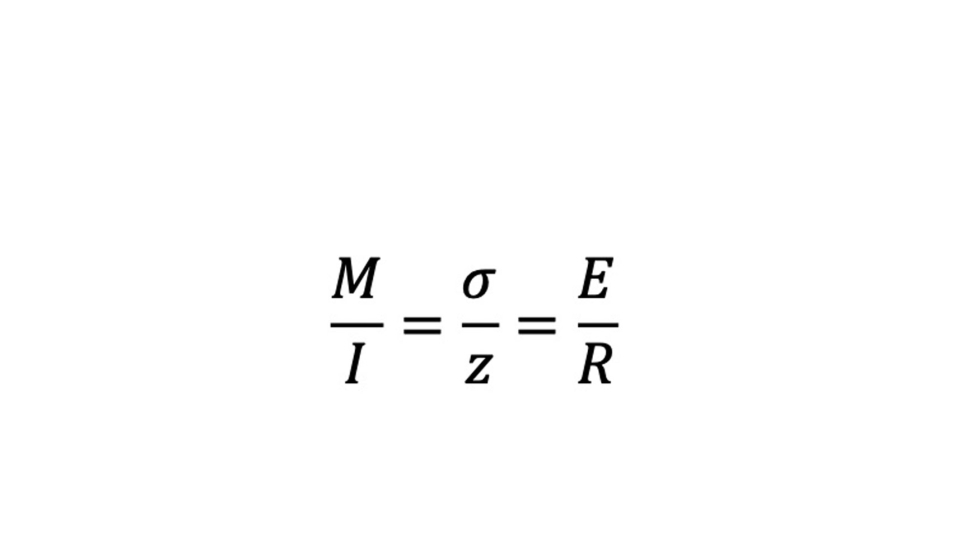
M Momento flector en Nm
I Momento de inercia en m4
σ Tensión normal en N/m2
z Distancia desde la línea neutra hasta el punto donde queremos saber la tensión en m
E Módulo elástico del material en N/m2
R Radio de curvatura de la línea neutra en m
De la ecuación de relación fundamental anterior obtenemos la siguiente igualdad:
σ/z=E/R, por lo que, σ=z E/R
Gracias a esta ecuación podremos calcular las tensiones a las que va a estar sometido el vidrio conociendo su espesor, su radio de curvatura y su módulo de elasticidad,
Debido a la incorporación de la normativa EN16612:2019, se puede determinar las tensiones maximas a las que el vidrio puede estar sometido en funcion del tratamiento de sus cantos y del tratamiento térmico, así como a las cargas a las que puede estar sometido el vidrio, llegando a las siguiente consideraciones:
Tensión de diseño para vidrio:
Vidrio recocido en posición vertical sometido a carga de viento con canto pulido industrial,
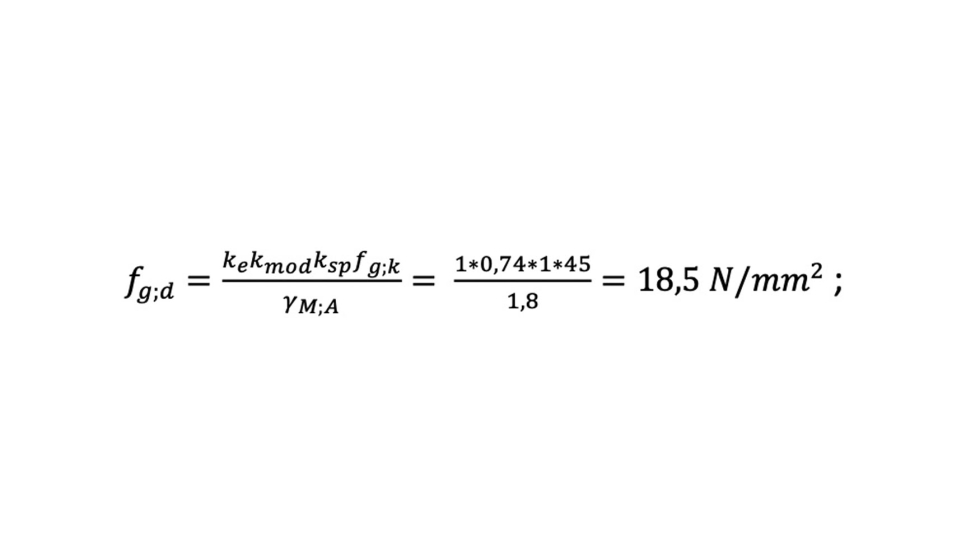
Vidrio recocido en posición vertical sometido a carga de viento con arista abatida,
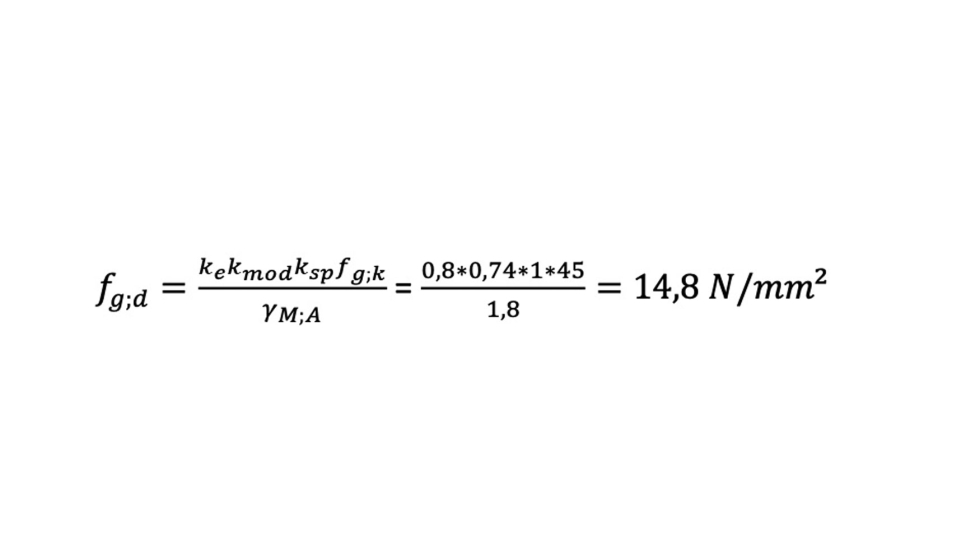
Vidrio recocido sometido a cargas permanentes con canto pulido industrial,
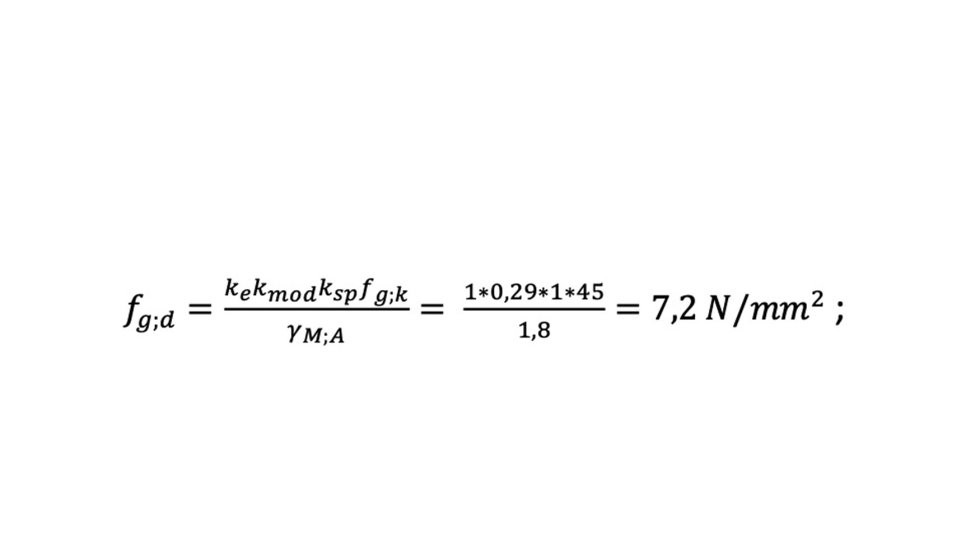
Vidrio recocido sometido a cargas permanentes con arista abatida,
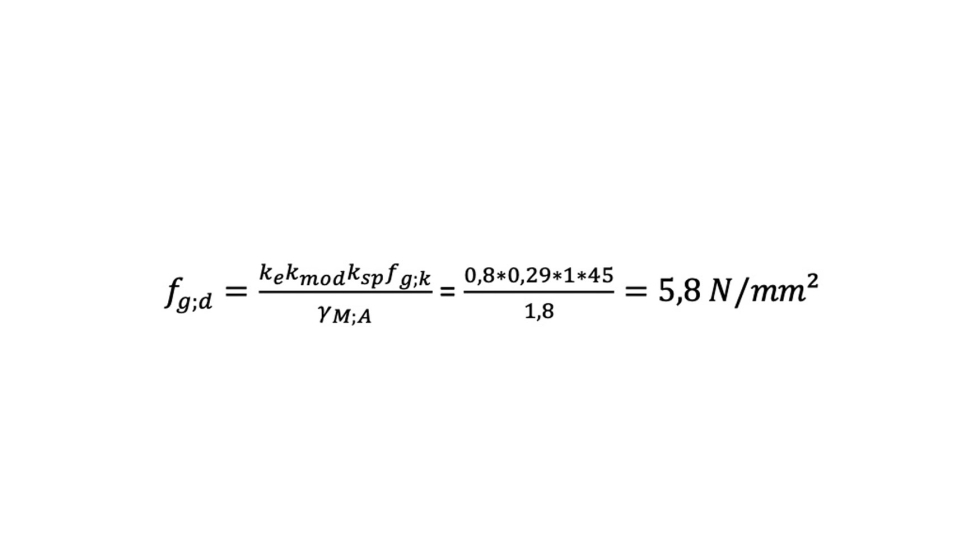
Vidrio tratado térmicamente termoendurecido en posición vertical sometido a cargas de viento

Vidrio tratado térmicamente termoendurecido sometido a cargas permanentes

Vidrio tratado térmicamente templado, sometido a cargas de viento
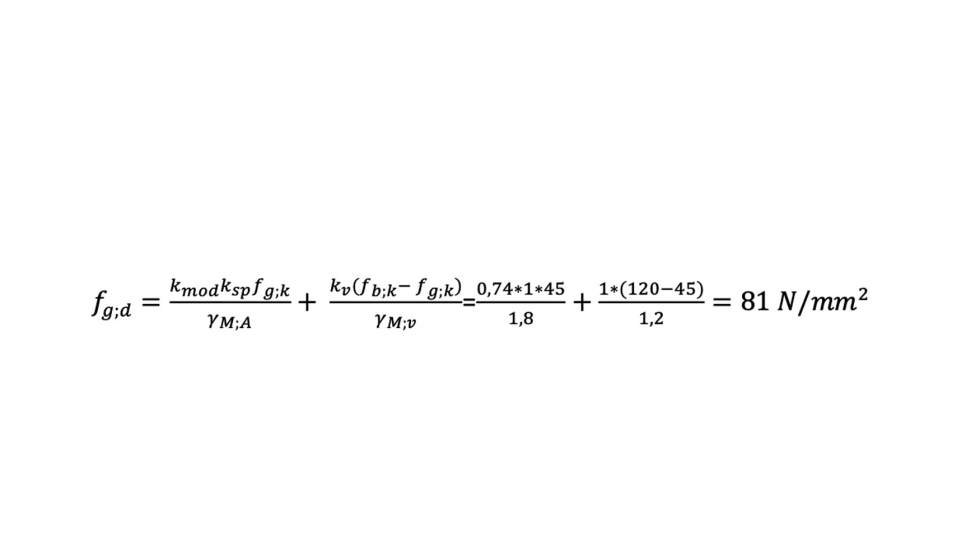
Vidrio tratado térmicamente templado sometido a cargas permanentes (esta es la resistencia que consideramos para el vidrio curvado en frío ‘in situ’)

Vidrio esmaltado tratado térmicamente templado sometido a cargas de viento

Vidrio esmaltado tratado térmicamente templado sometido a cargas permanentes

La tabla adjunta muestra la tensión a la que va a estar sometido un vidrio de un espesor determinado para un radio de curvatura dado.
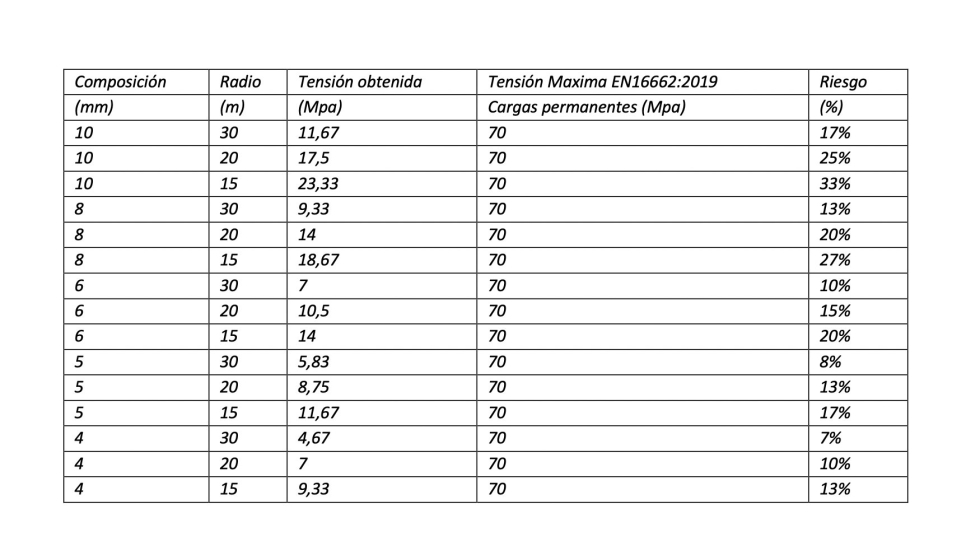
En el caso de un vidrio laminado, los valores de la tabla seguirían siendo válidos utilizando en lugar del espesor total del laminado, su espesor equivalente.
Método simplificado para el cálculo de vidrio laminado conforme a EUROCODIGO 16612:2019
El cálculo preciso de la tensión y la flecha del vidrio laminado es complejo. El intercalario es viscoelástico y su módulo de tracción y su módulo de cizalladura pueden variar considerablemente para diferentes temperaturas y cuando está en tensión para diferentes duraciones. Se requiere un detallado conocimiento de las condiciones probables de servicio y de la naturaleza de las acciones sobre el vidrio para determinar el módulo de cizalladura apropiado para usar en los cálculos de resistencia de carga. La reacción del vidrio a las acciones tambien necesita una herramienta sofisticada de análisis para determinar las reacciones de forma precisa.
No es realista realizar cálculos tan sofisticados para cada simple aplicación del vidrio. Por ello es necesario un método fácil de cálculo que facilite una selección segura del vidrio laminado para estas aplicaciones.
El método simplificado deberá usarse solo para hojas de vidrio apoyadas linealmente sometidas a cargas uniformes.
El espesor equivalente para calcular la flecha por flexión es:

Y el espesor equivalente para calcular la tensión de la capa número j del vidrio es:

ω es un coeficiente entre 0 y 1 que representa: sin transferencia de cizalladura (0) y plena transferencia de cizalladura(1).
hi Espesor nominal de la capa de un vidrio i laminado
hj Espesor nominal de la capa de un vidrio j laminado
hk Espesor nominal de la capa k de un vidrio laminado
hm;i Distancia entre el vidrio plano medio de la capa i y el plano medio del vidrio laminado
hm;j Distancia entre el vidrio plano medio de la capa j y el plano medio del vidrio laminado
hm;k Distancia entre el vidrio plano medio de la capa k y el plano medio del vidrio laminado
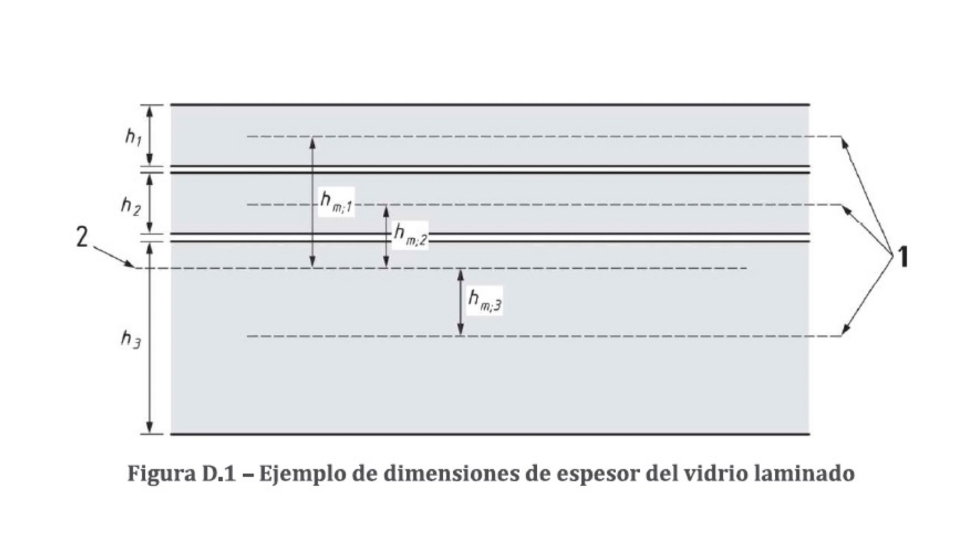
Determinación de ω
Cada intercalario tiene un coeficiente de transferencia de cizalladura asignado par aun número de diferentes conidiciones de carga según el método de ensayo y la evaluación de la Norma EN16613. Las condiciones de carga se indican en la tabla D.2
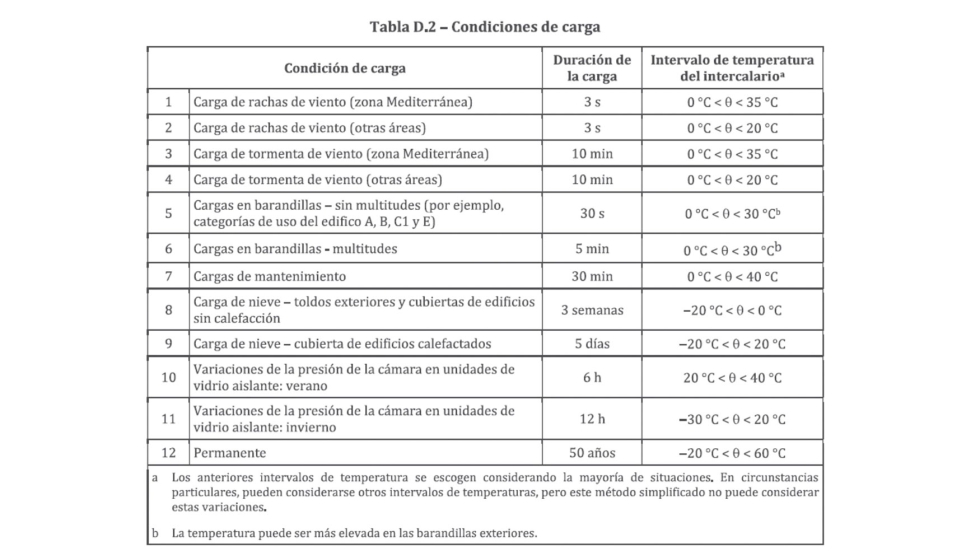
El valor de ω que se usa para un intercalario específico y una condición de carga particular depende de la rigidez de la familia del intercalario a la que pertenece para esa condición de carga particular.
La rigidez de las familias de intercalarios y los valores equivalentes de ω se indican en la tabla D.3.
Cualquier intercalario cuyas propiedades no se hayan evaluado siguiendo la Norma EN 16613 debería considerarse que pertenecen a la familia 0 de rigidez.
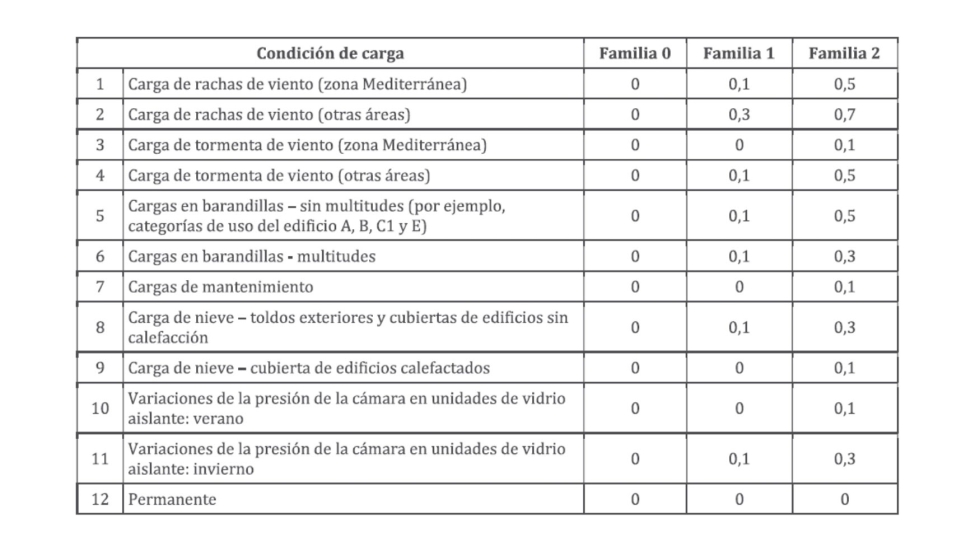
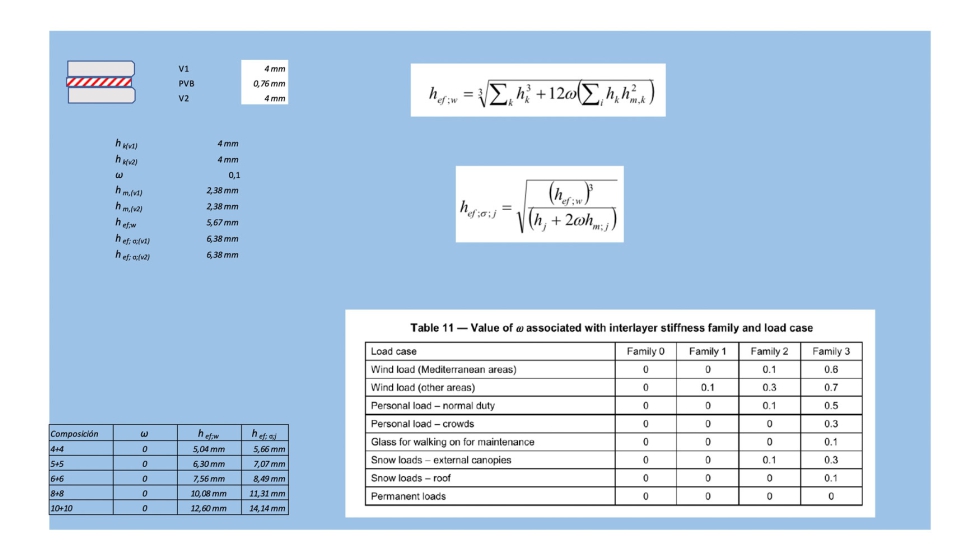
Tabla 2.3. Valor de ω asociado a la rigidez de la familia del intercalario y la condición de carga.
Cuando se usan los valores inferiores del coeficiente de transmisión de la cizalladura normalmente se producen tensiones y flechas superiores en el vidrio, por lo que se debería tener cuidado en no pasar por alto las condiciones de cargas si al usar un valor elevado del coeficiente de transferencia de la cizalladura se produce una condición de tensión más elevada. Esto suele perjudicar principalmente a las unidades de doble acristalamiento.
Para el caso que nos atañe vamos a determinar el espesor equivalente para tensiones teniendo en cuenta que el vidrio laminado de seguridad se encontrará sometido a cargas permanentes, por lo tanto ω=0.

Aplicando la fórmula de espesor equivalente de vidrio laminado para para tensiones, obtenemos que:
Por ejemplo, para un vidrio 4+4.1 (1 x 0,38mm PVB incoloro)

De estas fórmulas obtendremos los espesores equivalentes para los laminados mas comúnes, siendo:
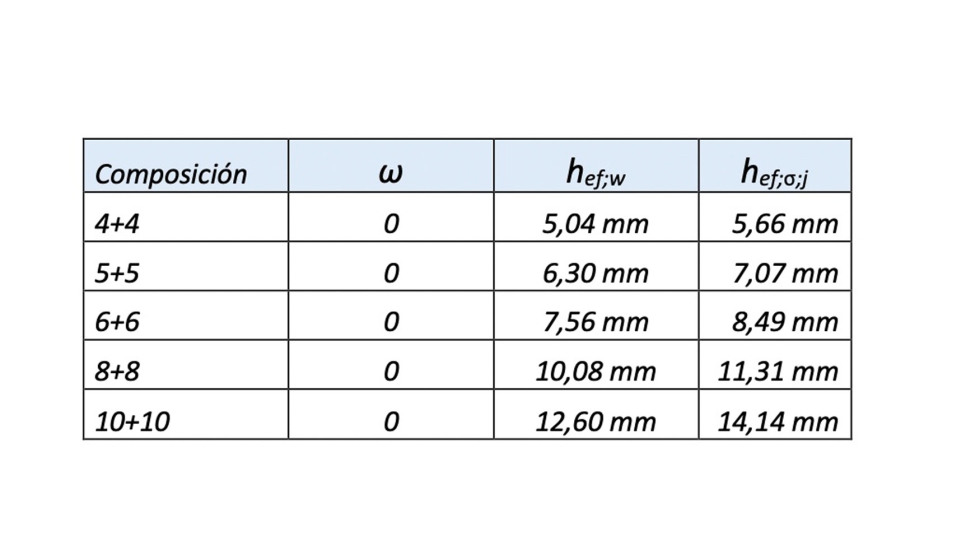
Una vez conocida la curvatura y cargas externas a las que se verá sometido el vidrio, podremos determinar el espesor óptimo necesario.
Conclusiones
El vidrio plano puede adoptar formas curvadas de diferentes radios en función de su elasticidad y su espesor.
El vidrio curvado se encuentra sometido a una carga permanente que le provoca una tensión lo que implica una pérdida en su resistencia mecánica frente a las cargas externas.
Una vez curvado en frío el vidrio, deberá soportar las cargas externas (variables y permanentes) a las que estará sometido. Por lo tanto la suma de las tensiones generadas por el curvado más las cargas externas, no podrá superar la tensión maxima admisible (para el caso de un vidrio templado sometido a cargas permantentes no puede superar los 70MPa).
BIBLIOGRAFÍA:
- UNE EN 16612:2019.
- Elementos de mecánica estructural. Francesc Arbos.
- CNR-DT 210/2013. Roma. 5/12/2013.
- Fachadas Ligeras. Manual de Producto 2015. Asefave.
Anexo 1
Imágenes de MECWAY con el modelo de estudio parametrizado,
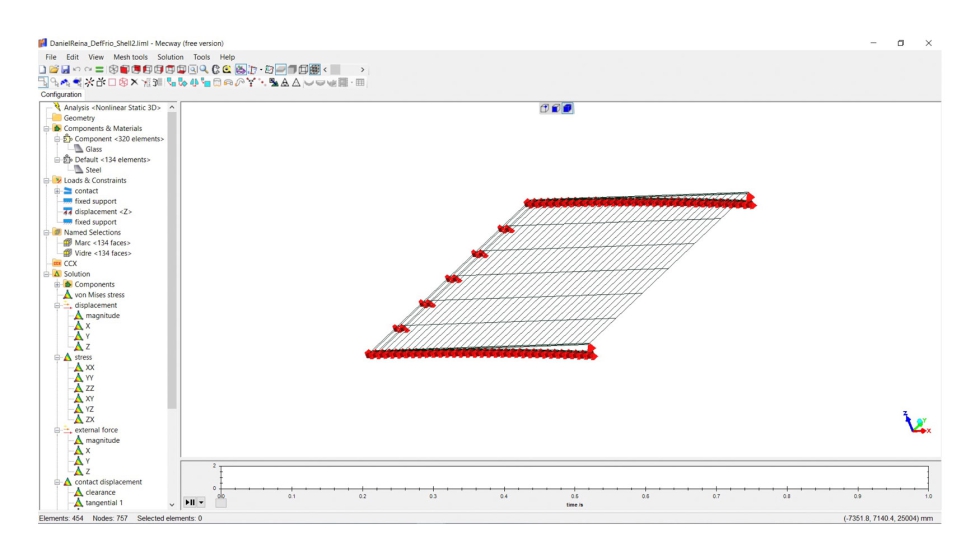
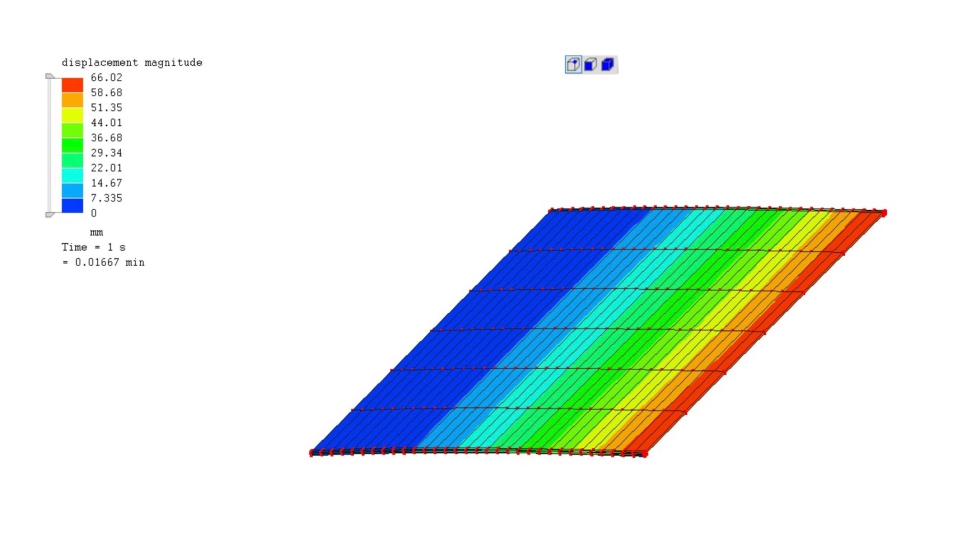
Anexo 2
La hoja de excel generada será capaz de determinar las tensiones del vidrio en función de su espesor y del radio de curvatura a adoptar.
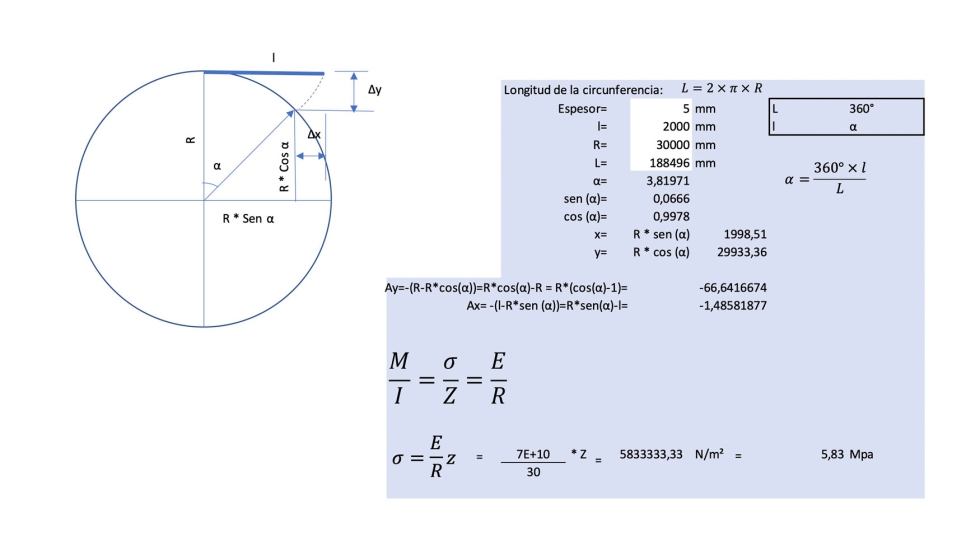
Anexo 3
Esta hoja excel permite determinar el espesor equivalente de un vidrio laminado para cálculo de tensiones.