Texturizado de superficies por medio de fresado en cinco ejes

En este artículo se desarrolla, en primer lugar, un modelo que permite predecir la geometría de las cavidades generadas a partir de unas determinadas condiciones de fresado. El método desarrollado incluye el efecto de la excentricidad radial (runout) de la fresa. En segundo lugar, se analiza la influencia de las condiciones de corte (inclinación y orientación de la fresa y avance) en la geometría de las cavidades generadas con el fin de determinar las condiciones de fresado necesarias para la obtención de cavidades con determinada geometría, sin necesidad de recurrir al método de prueba y error. Finalmente, se han llevado a cabo una serie de ensayos de fresado en cinco ejes para la validación del modelo. Se han comparado la geometría de las cavidades predichas por el modelo con cavidades generadas en los ensayos y se ha observado una buena correspondencia entre ellas.

En los últimos años, los procesos de texturizado de superficies para mejorar las propiedades superficiales de piezas están teniendo un interés creciente. En la bibliografía, se han publicado trabajos que presentan el estado del arte en el texturizado de superficies. En 2008, Bruzzone et al. [1] publicaron un artículo en el cual se presentan propiedades superficiales que pueden verse afectadas por el texturizado así como aplicaciones de las superficies funcionales. Algunos ejemplos de propiedades cuya mejora tiene interés industrial son la adhesión en piezas que deben ser recubiertas, la capacidad de repeler humedad, propiedades ópticas, propiedades hidrodinámicas, propiedades tribológicas, la disminución de la fricción entre superficies, la capacidad de almacenamiento de lubricante, etc. En este artículo [1], también se presentan tecnologías y procesos empleados en el texturizado de superficies y se clasifican en varios grupos según el principio físico en el que se basan. De entre estos grupos, se mencionan las tecnologías aditivas (procesos químicos de recubrimiento y procesos de deposición física) y las tecnologías sustractivas (láser, procesos de ataque químico selectivo o mecanizado) de material. Recientemente, teniendo en cuenta la clasificación de Bruzzone et al. [1], Coblas et al. en [2], Arslan et al. en [3] e Ibatan et al. [4] describen los procesos y tecnologías de texturizado empleados actualmente en la fabricación industrial destacando sus ventajas, inconvenientes y limitaciones.

Una aplicación del texturizado que presenta gran interés en los últimos años es el texturizado de la cara de desprendimiento de las herramientas de corte. En [3], se realiza un estudio de los trabajos de investigación llevados a cabo en el desarrollo de herramientas de corte texturizadas para torneado, fresado y taladrado. En este trabajo, se hace también referencia a la forma, profundidad y espaciado de las texturas así como a las mejoras aportadas en el rendimiento de las herramientas en cuanto a adhesión (filo recrecido), reducción de fricción en la cara de desprendimiento, desgaste de cráter, incremento de vida de la herramienta, reducción de las fuerzas de corte, etc.

Otra aplicación muy extendida de las superficies funcionales es la mejora de las propiedades tribológicas [4], [5], [6], [7]. La reducción de la fricción entre dos superficies en movimiento tiene un efecto directo en la eficiencia y en el consumo de energía y proporciona una disminución del desgaste. Normalmente, la textura superficial en este tipo de aplicaciones consiste en cavidades con una determinada profundidad, que se distribuyen de manera uniforme a lo largo de la superficie de la pieza. En el caso de texturizar superficies con cavidades, en la bibliografía se suele caracterizar la superficie a partir de la geometría, la forma, el área y la densidad de área de las cavidades en la superficie de la pieza, expresada en porcentaje. A continuación, se mencionan dos casos en los cuales las dimensiones de las cavidades son de la misma magnitud que las estudiadas en este trabajo.

En [5], se emplean micro-cavidades con formas circular y elíptica de semi-eje mayor de 732 micras y menor de 366 micras, profundidad 55 micras y densidad 40 % en discos de acero inoxidable. Se analiza la influencia en la disposición de las cavidades en la superficie del disco y se observa una disminución del coeficiente de fricción en la superficie texturizada con respecto a la superficie sin texturizar. En este trabajo, para la obtención de las cavidades se emplea un texturizado por laser. En [7], se obtienen cavidades por medio de otros procesos: en primer lugar, se realiza una operación de bruñido y posteriormente, una operación de rectificado para eliminar protuberancias creadas en la superficie. En este caso, las dimensiones de las cavidades varían entre diámetros de 160-300 micras, profundidades de 17-60 micras y densidades 3-12%. En este trabajo, se alcanza una reducción del 60% en los valores del coeficiente de fricción en un determinado rango de velocidad de trabajo.

Los procesos más empleados en el texturizado de superficies se basan en el laser (laser surface texturing), en el chorro de iones (ion beam surface texturing) y en el ataque químico selectivo (etching surface texturing) pero debido a que el equipamiento necesario es caro, estas aplicaciones se justifican en piezas de muy alto valor añadido. Recientemente, se han publicado trabajos de investigación que han mostrado la posibilidad de texturizar superficies generando cavidades por medio de procesos de mecanizado si se eligen adecuadamente los parámetros de proceso. Estos trabajos se han centrado en el texturizado vibro-mecánico (Vibro mechanical texturing) ([8], [9], [10]) y en el fresado en cinco ejes con fresa de punta esférica ([11], [12], [13], [14]).

El texturizado vibro-mecánico es un método empleado para generar micro-cavidades en superficies cilíndricas. Se basa en una operación de torneado en la cual la herramienta de corte oscila a medida que avanza a lo largo de la superficie cilíndrica de la pieza que está girando. El sistema se compone de un fast tool servo (FTS) que controla el movimiento oscilatorio de la punta de la herramienta. Este movimiento oscilatorio crea micro cavidades en la superficie de la pieza. Las cavidades generadas por este método pueden tener las siguientes dimensiones: profundidad de 2 a 50 micras y diámetro de 100 a 500 micras. Este proceso ha sido empleado para generar micro-cavidades con el propósito de reducir la fricción de piezas cilíndricas [8].

Recientemente, algunas publicaciones científicas han mostrado que el fresado con fresa de punta esférica puede ser capaz de texturizar las superficies generando cavidades si se eligen adecuadamente los parámetros de proceso. Variando la inclinación y orientación de la fresa se pueden obtener cavidades con distintas formas y orientaciones. El texturizado es muy versátil y se puede conseguir cavidades con diferentes geometrías y orientaciones. En [11] y [12], la fabricación de micro cavidades en superficies planas se realiza por medio de operaciones de micro fresado en cinco ejes. En [13], se presenta un método para la generación de micro cavidades en la superficie cilíndrica de una pieza de revolución por medio de fresado. Otros trabajos [14] se han centrado en la optimización de las estrategias de acabado en fresado de cinco ejes con objeto de generar rugosidades superficiales que mejoren la adhesión de recubrimientos. Recientemente, en [15], se estudia la disminución del coeficiente de fricción de superficies texturizadas con fresa frontal con eje inclinado. Debido a la geometría de la fresa y al proceso de fresado, la forma de las cavidades es asimétrica en lugar de las formas de cavidad más comunes: circulares o elípticas. Los resultados de los ensayos realizados en un tribómetro muestran una disminución del coeficiente de fricción.

En este artículo, se desarrolla un modelo que predice la geometría de cavidades elípticas generadas en superficies planas por medio de operaciones de fresado de cinco ejes. El modelo tiene en cuenta el efecto de la excentricidad radial de la fresa. En segundo lugar, se analiza la influencia de los parámetros de proceso (geometría de fresa, condiciones de corte y excentricidad radial) en la geometría (forma, dimensiones, orientación y densidad superficial) de las cavidades con el fin de desarrollar un procedimiento que permita definir las condiciones de fresado necesarias para texturizar una superficie con la cavidad deseada. En tercer lugar, el modelo se valida experimentalmente comparando la geometría de cavidades predichas con la de cavidades creadas en ensayos de fresado. La validación se lleva a cabo para dos valores de excentricidad radial de la fresa.

La simulación de la topografía superficial generada en operaciones de fresado, en general, y de cavidades en fresado de cinco ejes en particular, requiere deducir las ecuaciones de las trayectorias descritas por los filos de corte durante la operación de mecanizado. En este apartado, se describe el modelo desarrollado para predecir la forma y dimensiones de las cavidades generadas teniendo en cuenta la geometría de la fresa, la excentricidad radial y las condiciones de corte.

2.1. Geometría de una fresa de punta esférica

En este trabajo, la generación de texturas superficiales en forma de cavidad se lleva a cabo por medio de fresas de punta esférica. En la figura 1a, se representa de manera esquemática la geometría de uno de los filos de una fresa de punta esférica de radio nominal R y ángulo de hélice a_hx. A este filo, se denomina filo 1 y se emplea como referencia para definir el sistema de coordenadas asociado a la fresa. Sin embargo, el modelo presentado a continuación se generaliza para fresas de N_t filos.

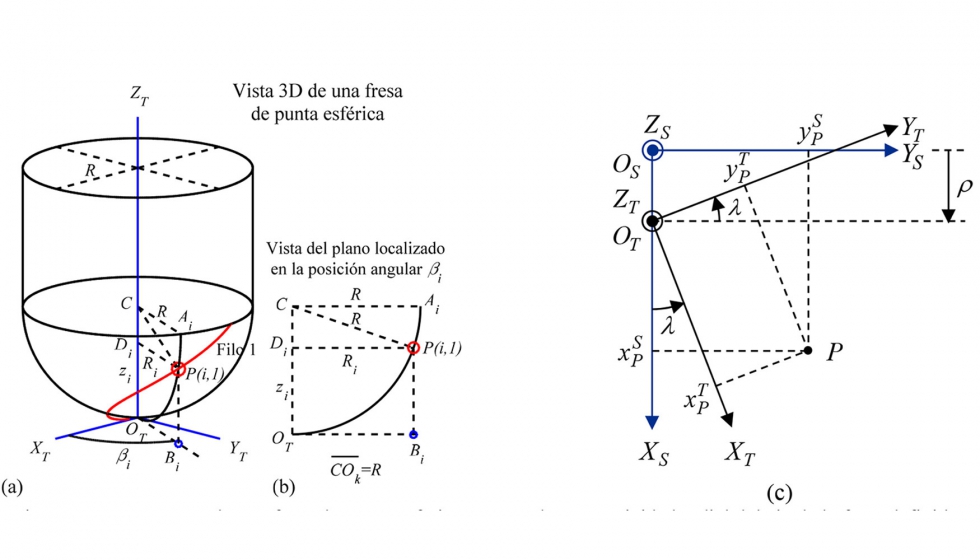
Figura 1: a) Geometría de una fresa de punta esférica en 3D y b) excentricidad radial del eje de la fresa definida por su magnitud ? y el ángulo de posición ?.

Para deducir las ecuaciones que expresan la posición de los puntos situados en los filos de corte de la fresa, se considera en primer lugar, un filo k, siendo k=1, 2, … N_t. En segundo lugar, se define un punto situado sobre el filo k a una altura z_i respecto de la punta de la fresa. En este trabajo, este punto se denomina como P(i, k). En la figura 1a, se muestra el punto P(i,1) correspondiente al filo 1 de la fresa. Para definir la posición de un punto cualquiera de la fresa, se considera un sistema de coordenadas O_TX_TY_TZ_T asociado a la fresa (figura 1a) en el cual:

• Su origen O_T se sitúa en el extremo libre de la fresa.
• El eje Z_T coincide con el eje de la fresa.
• El eje X_T tiene dirección radial y es tangente en el punto O_T a la proyección del filo 1.
• El eje Y_T es perpendicular a los ejes X_T y Z_T conformando un triedro.

La posición de un punto P(i, k), situado sobre el filo k a una altura z_i, viene determinada por los siguientes parámetros geométricos:

- La separación angular fk entre el filo k y el filo 1:

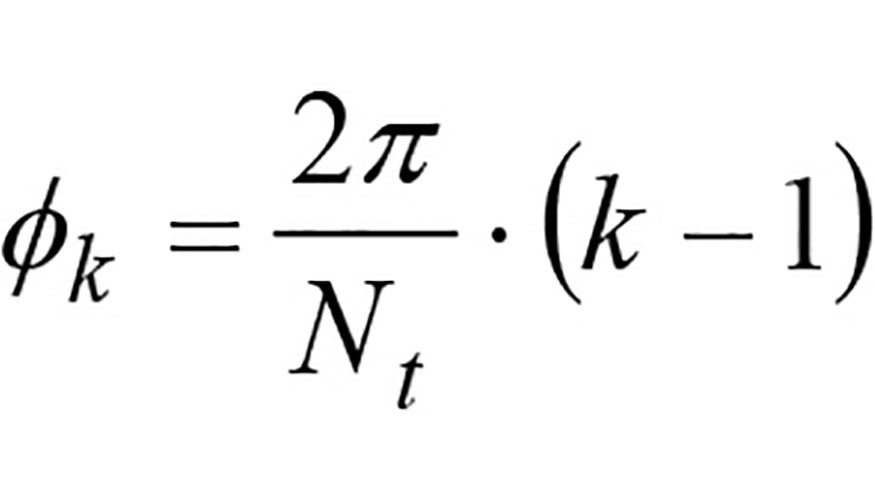
- La posición angular ß_i del punto P(i, k) respecto al punto más bajo del filo (figura 1a). Teniendo en cuenta el radio R y el ángulo de hélice a_hx, el ángulo ß_i se expresa como:

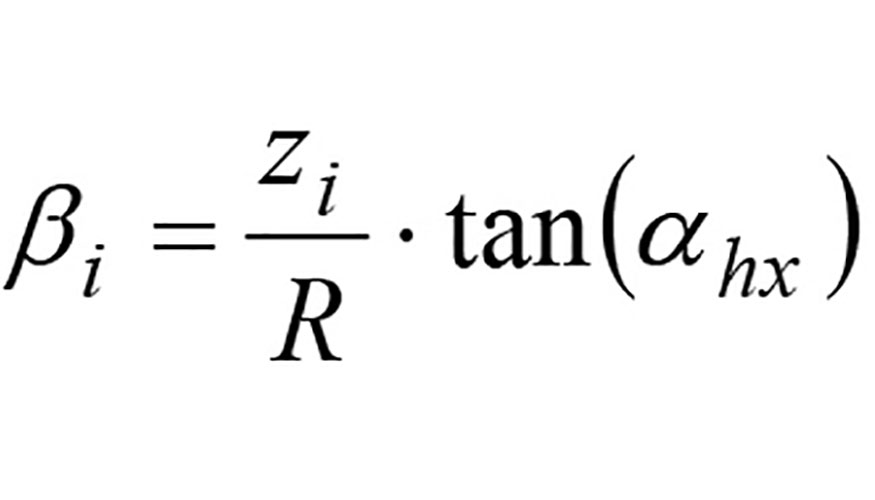
- La posición radial Ri del punto P(i, k) respecto al eje de la fresa (ver figura 1b):

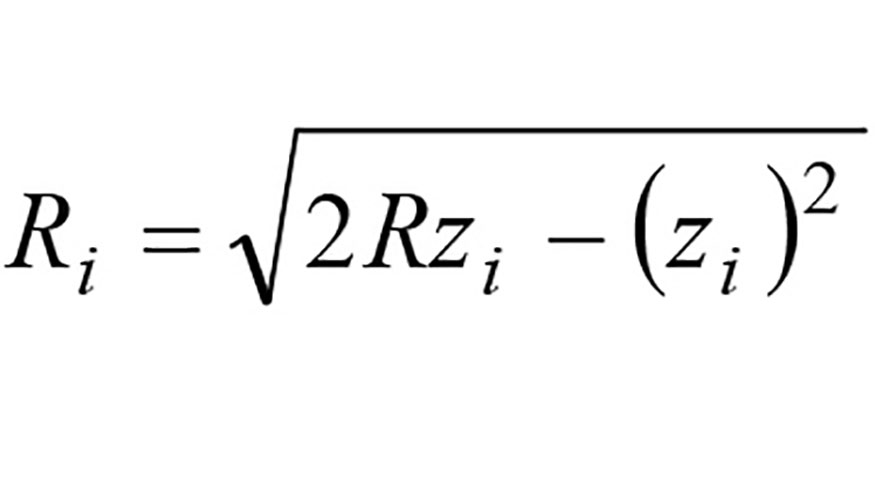
Finalmente, la posición del punto P(i, k) en el sistema de coordenadas X_TY_TZ_T se puede expresar en función de los parámetros R_i, ß_i y f_k definidos previamente como:

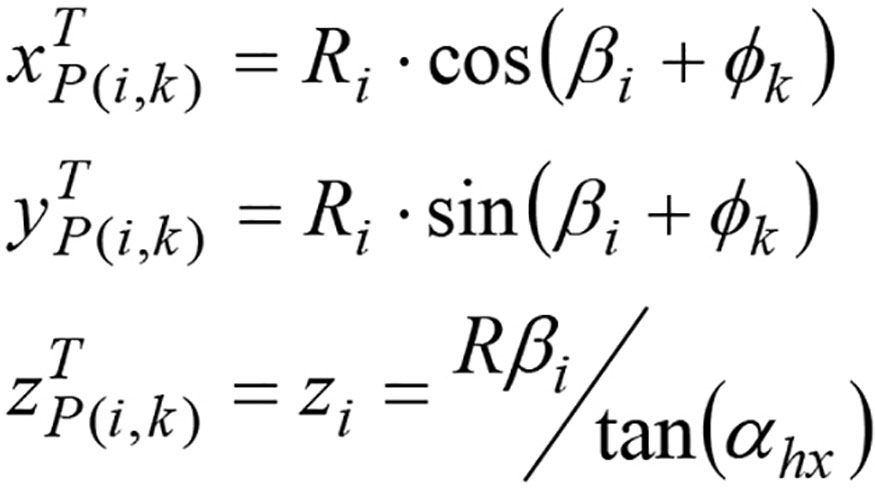
2.2. Excentricidad radial de la fresa

Al amarrar la fresa en el portaherramientas, el eje de la herramienta Z_T no coincide con el eje de giro Z_S del husillo (figura 1b). En esta comunicación, se supone que la fresa es rígida y que su eje Z_T presenta un error de excentricidad radial de valor ? con respecto al eje de giro Z_S del husillo. Debido a que los filos de corte giran con respecto al eje del husillo, la excentricidad radial influye de manera significativa en la trayectoria de los filos de corte de una fresa y por lo tanto, en la geometría de las cavidades generadas en la superficie. Por ello, se considera un sistema de coordenadas X_SY_SZ_S asociado al husillo (figura 1b) donde a) el eje Z_S coincide con el eje del husillo; b) O_S es el punto de intersección del eje Z_S con el plano X_TY_T; c) el eje X_S es la línea que une los puntos O_T y O_S y d) ? es el ángulo de posición del eje X_T con respecto al eje X_S. Las coordenadas del punto P(i, k) en el sistema asociado al husillo se puede expresar en función de la excentricidad radial ? y del ángulo ? como:

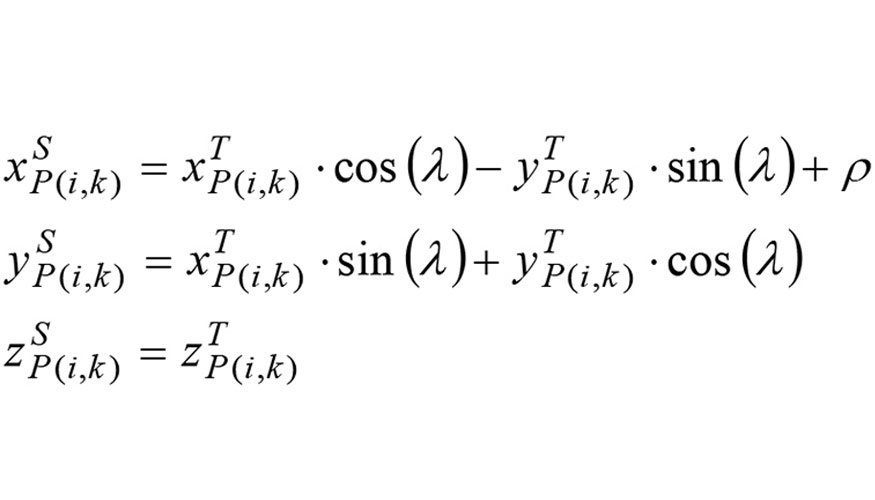
Una vez definida la posición de los filos en el sistema del husillo, se deducen las trayectorias descritas por los filos teniendo en cuenta las condiciones de corte definidas en fresado de cinco ejes.

2.3. Definición de las condiciones de corte para el fresado de cavidades

En la figura 2a, se muestra un esquema de la operación de fresado de cavidades en cinco ejes considerada en este trabajo, en el cual una fresa de punta esférica genera cavidades en la superficie plana de una pieza. Para simular la geometría de la cavidad generada, se define un sistema de referencia asociado a la pieza O_WX_WY_WZ_W (figura 2a) en el cual:

• El eje Z_W es perpendicular a la superficie plana de la pieza.
• El origen O_W está situado a una distancia a_P respecto a la superficie de la pieza. Esta distancia es la profundidad de pasada y determina la profundidad de las cavidades generadas.
• El eje X_W coincide con la dirección de avance de la fresa.
• El eje YW es perpendicular X_W y Z_W formando un triedro.

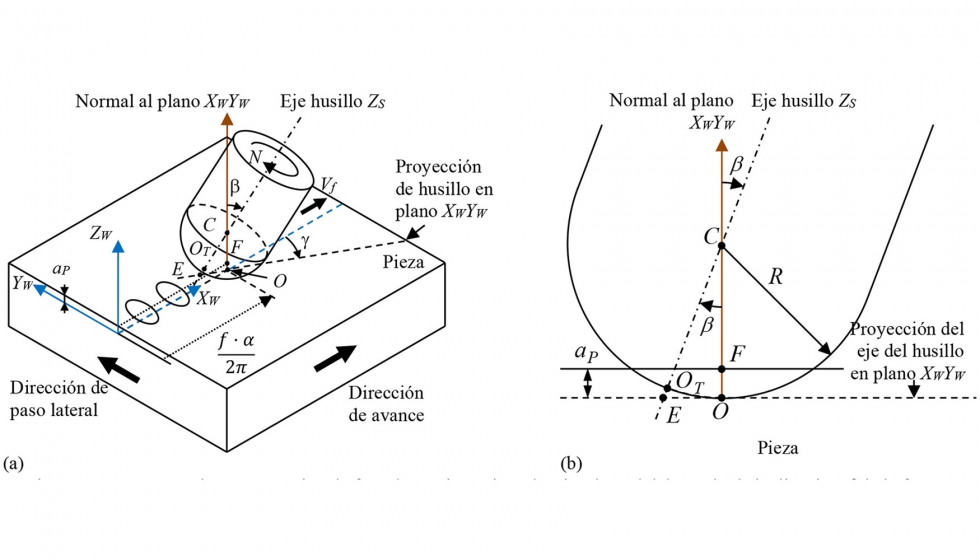
Como es sabido, durante la operación de fresado, la fresa gira con una velocidad de giro N y se desplaza con una velocidad V_f en la dirección de avance (figura 2a), avanzando una distancia f por cada revolución de la fresa. El avance por filo f_Z será igual a f/N_t. En este trabajo, se define un ángulo a, que representa el ángulo girado por el husillo. La distancia que avanza la fresa, cuando el husillo ha girado un ángulo a expresado en radianes, se puede expresar como f•a /2p.

Para la generación de estas cavidades, se emplean avances f elevados y profundidades de pasada a_P pequeñas en comparación con las condiciones de corte empleadas en las operaciones de fresado más comunes, con el fin de evitar interferencias entre cavidades generadas por diferentes filos de la fresa.

Como se puede observar en la figura 2, en la operación de fresado considerada en este trabajo, el eje del husillo no es perpendicular a la superficie de la pieza sino que a) está inclinado un determinado ángulo con respecto a la normal a la superficie (figura 2b) y b) se orienta otro determinado ángulo con respecto a la dirección de avance. Por lo tanto, la orientación del eje del husillo se define por medio de dos ángulos denominados en este trabajo como: el ángulo de inclinación ß y el ángulo de orientación ?. En la figura 2, por claridad, se supone que el eje de la fresa coincide con el eje de giro del husillo, es decir, no existe excentricidad radial en la fresa.

Para definir estos ángulos, se emplea el esquema de la operación de fresado mostrada en la figura 2a, en la cual se representan dichos ángulos ß y ?. Como se puede observar en la figura, el ángulo de inclinación ß es el ángulo formado entre el eje del husillo y la normal a la superficie de la pieza. Para facilitar la definición del ángulo de orientación ?, se considera en primer lugar la proyección del eje del husillo en el plano X_WY_W (ver figura 2a). El ángulo de orientación ? se define como el ángulo que forma dicha proyección con la dirección de avance X_W. Como se verá en los siguientes apartados, estos ángulos son parámetros que determinan la forma de las cavidades generadas. Durante la operación de fresado considerada en este trabajo, los ángulos ß y ? se fijan al inicio de la operación de fresado y se mantienen invariables a medida que avanza la fresa.

Una vez definidas las condiciones de fresado, para deducir las ecuaciones que expresan las trayectorias de los filos, es necesario transformar las coordenadas de los puntos de corte definidas en el sistema del husillo X_SY_SZ_S (ecuación (5) al sistema asociado a la pieza X_WY_WZ_W (figura 2) teniendo en cuenta la inclinación ? y orientación ß del husillo y las condiciones de corte (avance f y ángulo girado a). En esta comunicación, se emplea la transformación entre sistemas presentada con mayor detalle en [16], que se basa en el empleo de una serie de sistemas de coordenadas auxiliares y en la deducción de las matrices de transformación de coordenadas entre los sistemas. Teniendo en cuenta estas matrices de transformación, las coordenadas de un punto P(i, k) en el sistema asociado al husillo X_SY_SZ_S se puede expresar en el sistema de la pieza X_WY_WZ_W como:

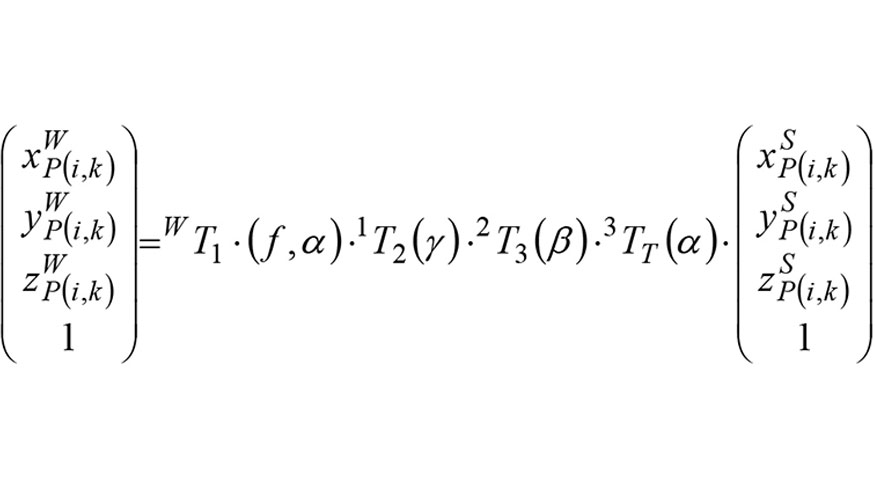
Donde las matrices de transformación se pueden expresar como:

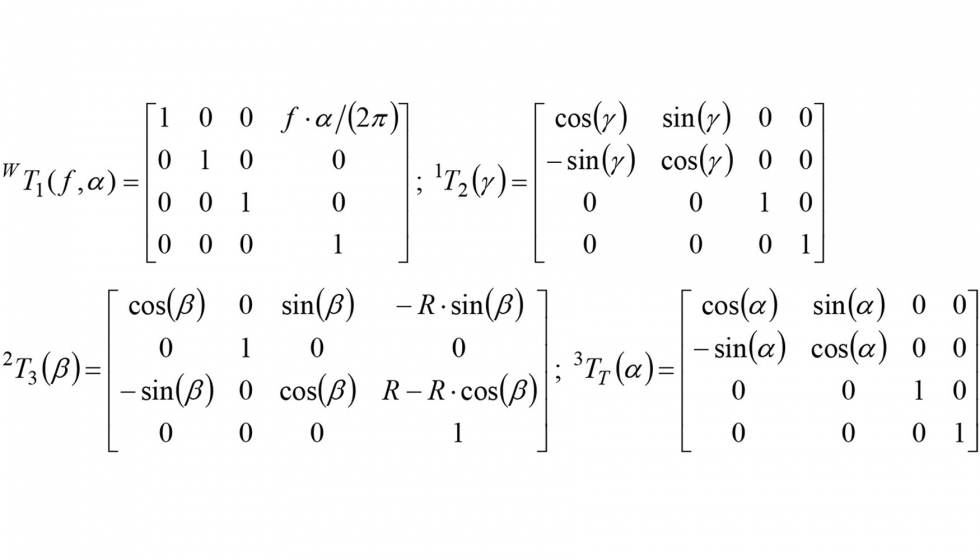
2.4. Trayectoria de los filos de corte

Sustituyendo las ecuaciones (4) en (5) y las ecuaciones (5) en (6), se obtienen las coordenadas de un punto P(i, k), situado a una altura z_i en el filo k, en el sistema de la pieza X_WY_WZ_W en función de las condiciones de corte, de la excentricidad radial y de la geometría de la fresa de punta esférica:

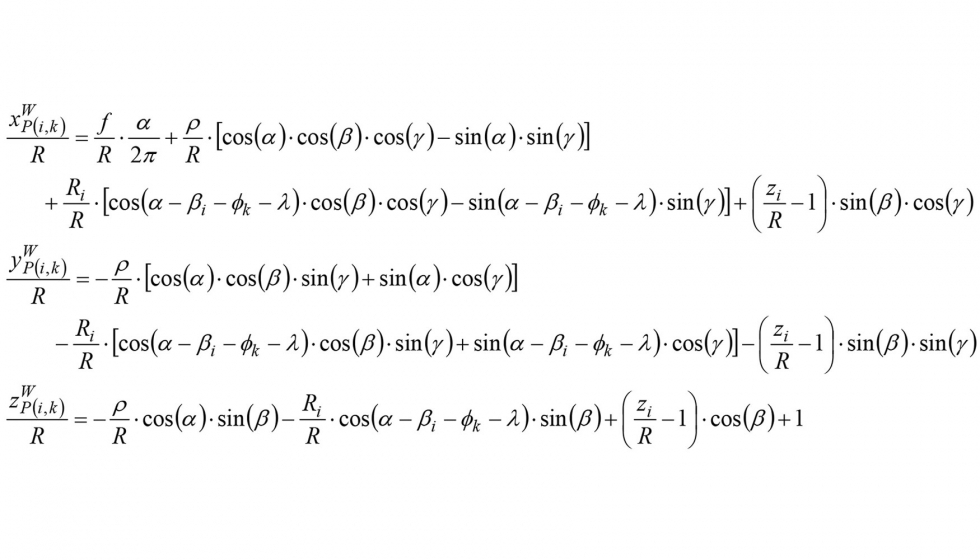
Finalmente, la trayectoria descrita por el punto P(i, k) en una operación de fresado en cinco ejes se obtiene variando el ángulo girado a en las ecuaciones (7). Por lo tanto, cuando se simula el movimiento realizado por los filos de corte, la trayectoria de un punto situado en un filo de corte de la fresa está compuesta por una serie de puntos que se calculan para distintos valores del ángulo a a lo largo del giro del husillo.

2.5. Simulación de cavidades generadas en fresado de cinco ejes

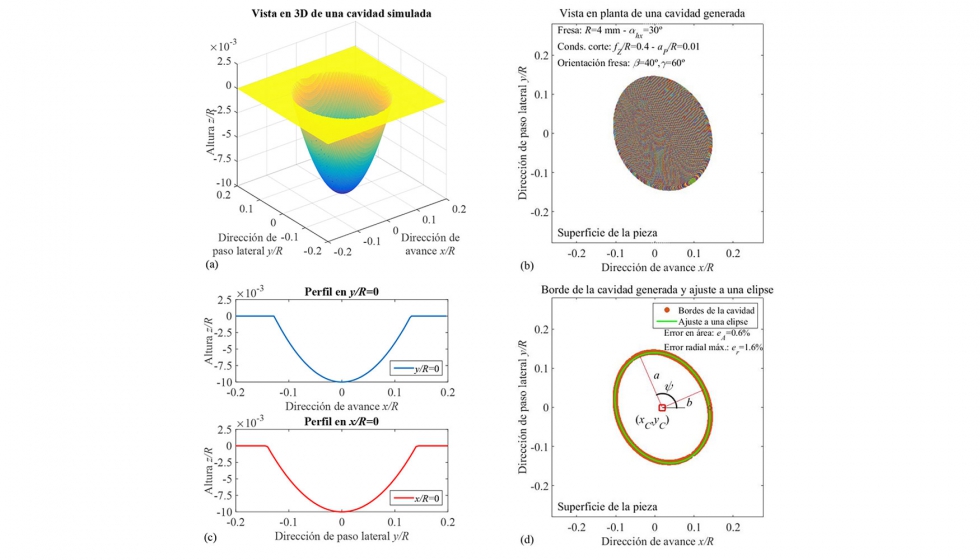
En la figura 3, se muestra la simulación de una cavidad generada en la superficie de una pieza fresada en cinco ejes. La cavidad corresponde a la huella dejada por un filo de corte de la fresa en la superficie de la pieza. Para ello, se requiere la simulación de las trayectorias descritas por diferentes puntos situados en un mismo filo de corte. Por lo tanto, para simular la cavidad, los filos de corte de la fresa se discretizan en un número finito de puntos, para los cuales se simula la trayectoria a medida que el husillo gira. Como se ha mencionado anteriormente, cada trayectoria está formada por una serie de puntos. De entre estos puntos, se seleccionan aquellos puntos de la trayectoria que están por debajo de la superficie de la pieza. Repitiendo este proceso para todos los puntos del filo discretizado, se obtiene una nube de puntos que conforma la cavidad simulada. En la figura 3b, se representan los puntos de las trayectorias de los filos de corte, que están situados por debajo de la superficie de la pieza. Estos puntos definen la forma y geometría de la cavidad simulada. Para las condiciones simuladas en la figura 3, la cavidad en la superficie de la pieza se asemeja a una forma elíptica (figura 3b). En la figura 3c, se representan los perfiles de la cavidad a lo largo de la dirección de avance en el plano (y=0) y a lo largo de la dirección de paso lateral (x=0).

Con el fin de analizar la forma y dimensiones de las cavidades generadas, a partir de los puntos que conforman la cavidad (ver figura 3b), se obtienen los puntos que definen el contorno de la cavidad en la superficie de la pieza (figura 3d). A partir de estos puntos, se ajusta el contorno a una elipse para obtener las dimensiones de la cavidad. El ajuste se realiza por medio del método de los mínimos cuadrados. El objetivo del ajuste es obtener una serie de parámetros que caracterizan la forma y dimensiones de las cavidades (figura 3d):

- (x_C, y_C): coordenadas del centro de la elipse.

- a, b: semiejes mayor y menor de la elipse.

- ?: ángulo que forma el semi-eje mayor con la dirección de avance x.

Además de estos parámetros, se calculan dos errores que miden el ajuste del contorno de la cavidad a una elipse: 1) el error radial máximo e_r entre el contorno de la cavidad y el contorno de la elipse y 2) el error e_A cometido entre el área de la cavidad y el área de la elipse.

En este apartado, se analiza la influencia de las condiciones de corte (ángulos de orientación ? e inclinación ß de la fresa, el avance por filo f_Z y la profundidad de pasada a_P) y del radio nominal R de la fresa en la forma y dimensiones de la cavidad con objeto de desarrollar un procedimiento que permita obtener las condiciones de fresado necesarias para la obtención de cavidades con determinada orientación y forma. En primer lugar, por medio de la figura 4, se analiza la influencia de los ángulos de orientación ? y de inclinación ß en la forma y geometría de las cavidades, manteniendo constante el resto de condiciones de corte.

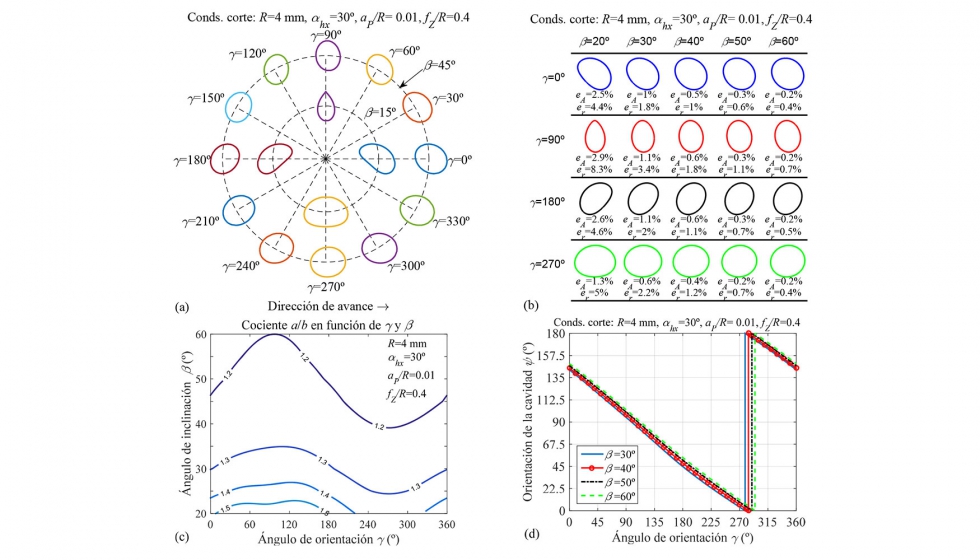
En la figura 4a, se muestra la influencia del ángulo de orientación ϒ en la geometría y orientación de las cavidades simuladas para dos ángulos de inclinación ß (15 y 45º). Para ambos ángulos de inclinación, se observa que el ángulo de orientación ϒ influye de manera significativa en la orientación de las cavidades generadas respecto a la dirección de avance (ángulo ψ en la figura 3d): para ϒ=270º, el semieje mayor de la cavidad sigue la dirección de avance mientras que para ϒ=90º, la dirección perpendicular. Respecto a la forma de las cavidades, se observa que, para ß=45º, las cavidades se asemejan a una forma elíptica independientemente del ángulo ?. En el caso de que el ángulo de inclinación fuera menor (ß=15º), las cavidades mantienen la orientación pero tienden a ser más alargadas y su forma cambia dejando de ser elípticas. Esta tendencia se puede visualizar en la figura 4b. A medida que el ángulo de inclinación ß disminuye, las cavidades dejan de tener una forma elíptica y son más irregulares, aumentando tanto el error radial máximo er como el error en el área e_A al compararlas con las elipses ajustadas por mínimos cuadrados.

En la figura 4c, se representa el cociente a/b entre los semiejes mayor a y menor b de las elipses en función de los ángulos ϒ y ß. En esta figura, se observa que, a medida que disminuye ß, el cociente a/b es cada vez mayor para cualquier ángulo ϒ, es decir, la forma de las cavidades es más ovalada. Esta tendencia es más significativa para valores de ϒ comprendidos entre 0 y 225º. Sin embargo, para ángulos ß entre 30º y 60º, el cociente a/b se mantiene prácticamente constante (alrededor de 1.2) independientemente del ángulo ϒ.

Con respecto a la orientación ψ de las cavidades, la figura 4d muestra que la orientación ψ varía de manera lineal con el ángulo ϒ pero apenas depende de la inclinación ß de la fresa. A partir de la tendencia mostrada en la figura 4d, dada una orientación ψ de cavidad deseada, se puede determinar el ángulo de orientación ϒ necesario para obtener dicha orientación en las cavidades.

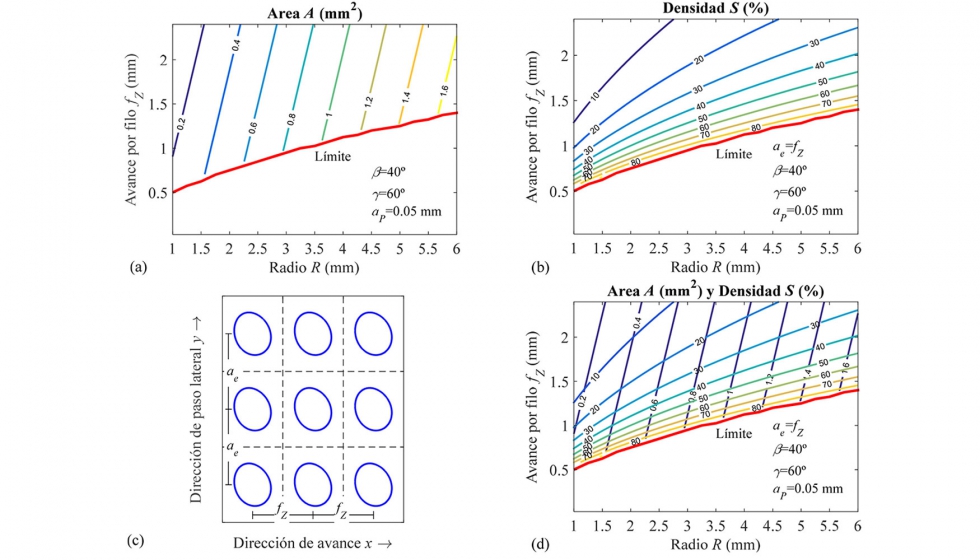
Una vez analizada la influencia de los ángulos ? y ß, se estudia la influencia del radio nominal R de la fresa y del avance por filo f_Z en el área A (figura 5a) y en la densidad superficial S (figura 5b) de las cavidades, manteniendo constante el resto de parámetros (inclinación ß, orientación ? y profundidad de la cavidad a_P). En la figura 5b, se considera que el paso lateral ae es igual al avance por filo f_Z de manera que las distancias entre cavidades en las direcciones de avance x y de paso lateral y son iguales (figura 5c).

En las figuras 5a, b, se representa una curva límite definida por combinaciones de radio R y avance por filo f_Z, para las cuales las cavidades generadas con los parámetros definidos previamente (ß, ? y a_P) no se solapan entre sí. Es decir, para cualquier combinación (R, f_Z) situada por debajo de dicha curva límite, las cavidades generadas por los filos se solapan y dejan de generarse cavidades en la superficie. Se observa que, a medida que el radio R crece, el avance por filo f_Z mínimo para evitar el solape entre cavidades crece. En dichas figuras, se representan, por encima de la curva límite, una serie de curvas de nivel correspondientes a distintas áreas y densidades de cavidad obtenidas para la profundidad de cavidad a_P. Estas curvas permiten definir la combinación (R,f_Z) para la cual se obtiene un área y una densidad determinadas con dicha a_P. Esta combinación sería aquella para la cual la curva de nivel del área A corta a la curva de nivel de la densidad S (figura 5c). De esta forma, se obtiene el radio R de la fresa y el avance por filo f_Z para los cuales, con los ángulos ß y ?, se genera una textura formada por cavidades de profundidad aP y con el área y la densidad deseadas. Si la separación entre cavidades en la dirección de paso lateral y fuera distinta, las curvas de nivel correspondientes a la densidad S cambiarían y en consecuencia, la combinación (R, f_Z). El procedimiento que permite definir las condiciones de fresado necesarias para texturizar una superficie con cavidades elípticas con una geometría (área y densidad) y profundidad aP dadas, consistiría en determinar: 1º) el ángulo de inclinación ß que asegure una forma elíptica, 2º) el ángulo de orientación ? que genera cavidades con una determinada orientación ? y 3º) la combinación de radio de fresa R y avance por filo f_Z, que garantice un área A y una densidad S de cavidades de profundidad aP en la superficie de la pieza.

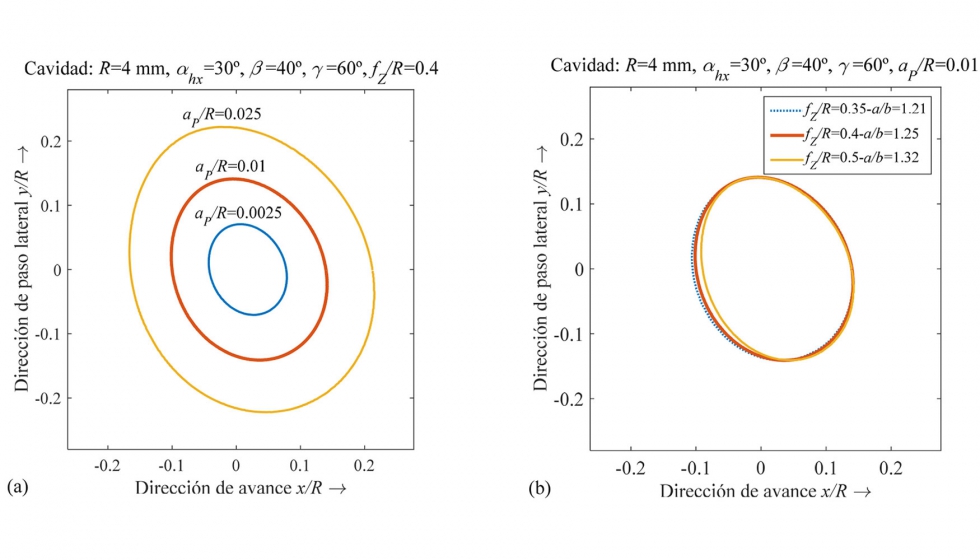
En la figura 6a, se analiza la influencia de la profundidad de pasada a_P en la geometría de la cavidad. Conforme la profundidad aP aumenta, las dimensiones de las cavidades aumentan pero su orientación y su forma (cociente entre semiejes) no cambian. En la figura 6b, se muestra la influencia del avance por filo f_Z. A medida que disminuye el avance por filo, la cavidad pasa de tener forma elíptica a una forma más circular, disminuyendo el cociente a/b entre semiejes de 1.32 a 1.21 para los avances simulados en la figura. Si el avance disminuyera, el cociente a/b tendería a 1.

La figura 7 muestra la evolución del cociente a/b y de la orientación ψ de la cavidad en función del ángulo de orientación ϒ para distintos avances por filo f_Z. En la figura 7a, se observa que: 1) para un avance f_Z, el cociente a/b no se mantiene constante conforme ϒ cambia y 2) para cualquier ángulo de orientación ϒ, el cociente a/b es mayor a medida que el avance por filo f_Z crece. Sin embargo, teniendo en cuenta la figura 7b, el avance por filo f_Z no influye en la orientación ψ de la cavidad.

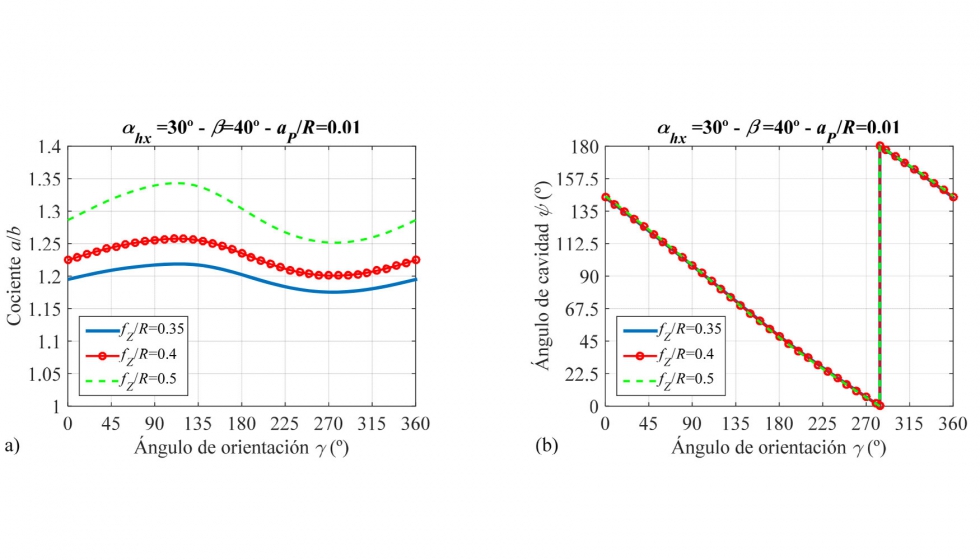
Figura 7. Influencia del avance por filo f_Z en: a) el cociente a/b entre semiejes y b) el ángulo ψ de la cavidad en función del ángulo de orientación ϒ.

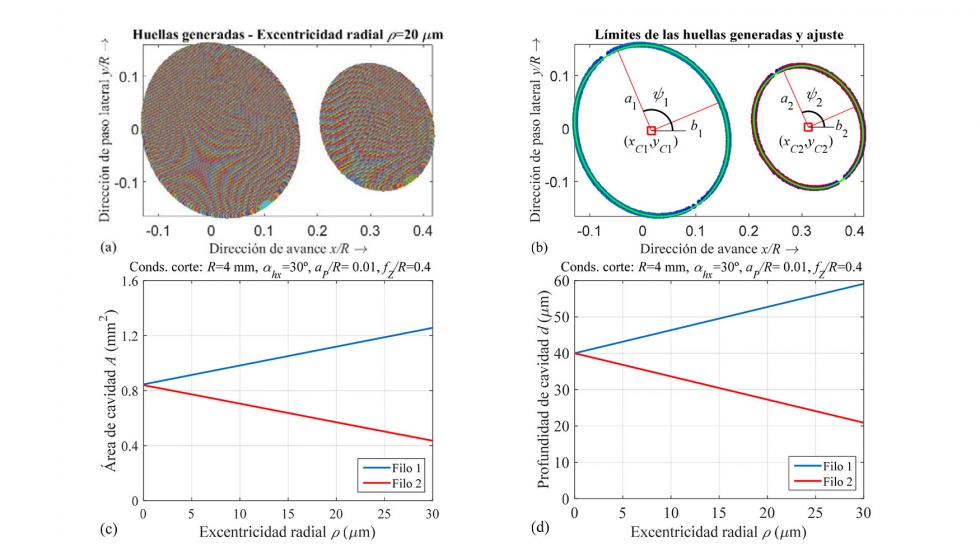
Uno de los parámetros que influye de manera significativa en la geometría de las cavidades es la excentricidad radial de la fresa. En las simulaciones anteriores, se ha supuesto que la excentricidad es nula. Sin embargo, al amarrar la fresa en el portaherramientas, la excentricidad puede dar lugar a cambios en la geometría de las cavidades. En la figura 8, se estudia el efecto de la excentricidad tanto en la forma como dimensiones de las cavidades. Al tener en cuenta la excentricidad, se observa que las cavidades generadas por cada filo de la fresa son distintas (figura 8a-b). La figura 8c-d muestra la influencia de la excentricidad en el área y en la profundidad de las cavidades generadas por cada filo de la fresa. Se observa una tendencia lineal en la variación del área y de la profundidad con la excentricidad.

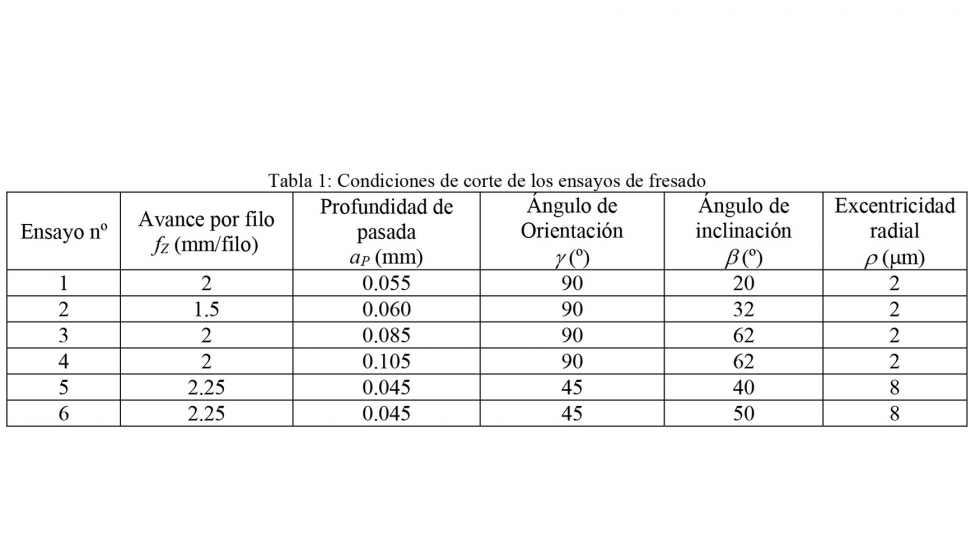
Se han realizado una serie de ensayos de fresado en un centro de mecanizado de 5 ejes para la validación experimental del modelo. Los ensayos han consistido en el fresado de cavidades en superficies planas de piezas de Al7075-T6. Para el fresado de las cavidades, se ha empleado una fresa de punta esférica de metal duro, Ø8 mm, 2 filos y ángulo de hélice 30º y una velocidad de giro de 2.000 rpm. La tabla 1 muestra las condiciones de fresado definidas para cada ensayo. Como se puede observar en la tabla 1, los ensayos se han realizado con dos valores de excentricidad radial distintos. La excentricidad radial se ha medido en el mango de la fresa por medio de un reloj comparador milesimal.

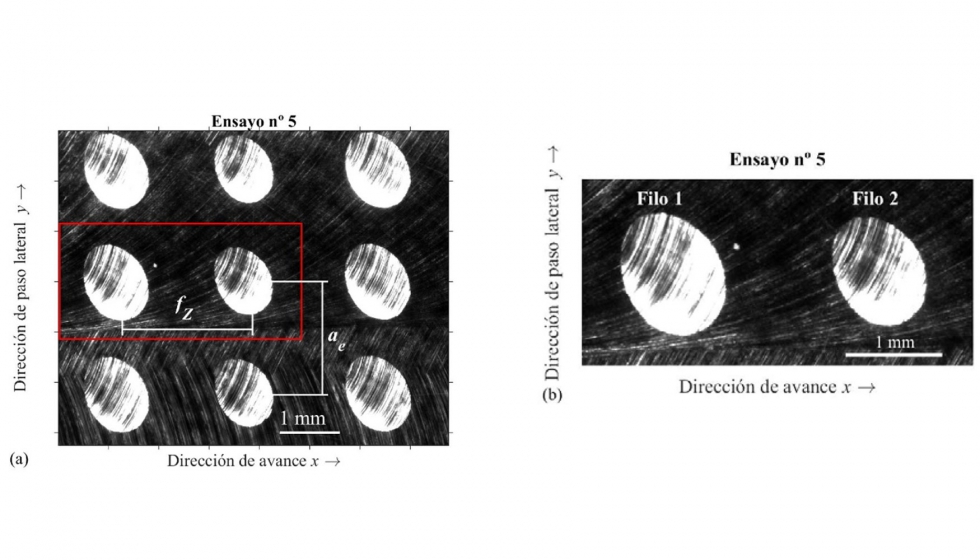
La validación de las predicciones del modelo se ha llevado a cabo por medio de la comparación de cavidades fresadas con cavidades simuladas. Para ello, tras el fresado de las cavidades, se han obtenido imágenes digitales de las cavidades (figura 9) y se han medido las cavidades por medio de un microscopio interferométrico de luz blanca (WLI) (figura 10). En la figura 9a, se muestra a modo de ejemplo, una imagen con las cavidades generadas en el ensayo 5. En la figura 9b, se representa una vista ampliada de dos cavidades. Cada cavidad está generada por un filo distinto de la fresa. En este ensayo, debido a la magnitud de la excentricidad radial de la fresa (?=8 µm), se puede apreciar una diferencia en las dimensiones de las cavidades. Cada filo deja en la superficie una huella distinta de manera que las dimensiones de las cavidades generadas por cada filo son distintas. En la figura 9b, las cavidades generadas por el filo 1 son más grandes que las generadas por el filo 2. A partir de las imágenes digitales, se ha obtenido el contorno de las cavidades aplicando un método de detección de bordes.

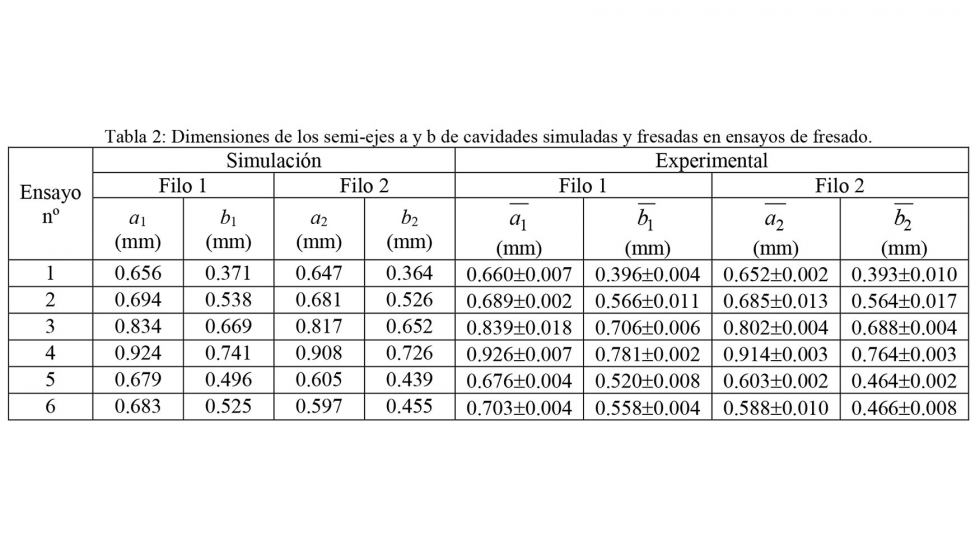
De manera semejante al procedimiento llevado a cabo con las cavidades simuladas, el contorno de las cavidades se ha ajustado a elipses por medio del método de mínimos cuadrados con el fin de obtener los semiejes mayor a y menor b de la cavidad. En la tabla 2, se comparan las dimensiones de los semiejes a y b obtenidos para cada filo en las simulaciones y en los ensayos, observándose una buena correlación entre ambos.

En la figura 10, se muestran dos cavidades obtenidas en el ensayo 5 que han sido medidas por medio del microscopio WLI. En la figura 10a-b, se representa una vista en planta de cavidades generadas por cada filo de la fresa. En dichas figuras, se visualiza el fondo y la profundidad de la cavidad. En figura 10c-d, se muestra el perfil de las cavidades en la dirección x. El perfil representado corresponde al plano medio de la cavidad a lo largo de la dirección y. En estas figuras, también se puede apreciar la forma y el fondo de las cavidades.

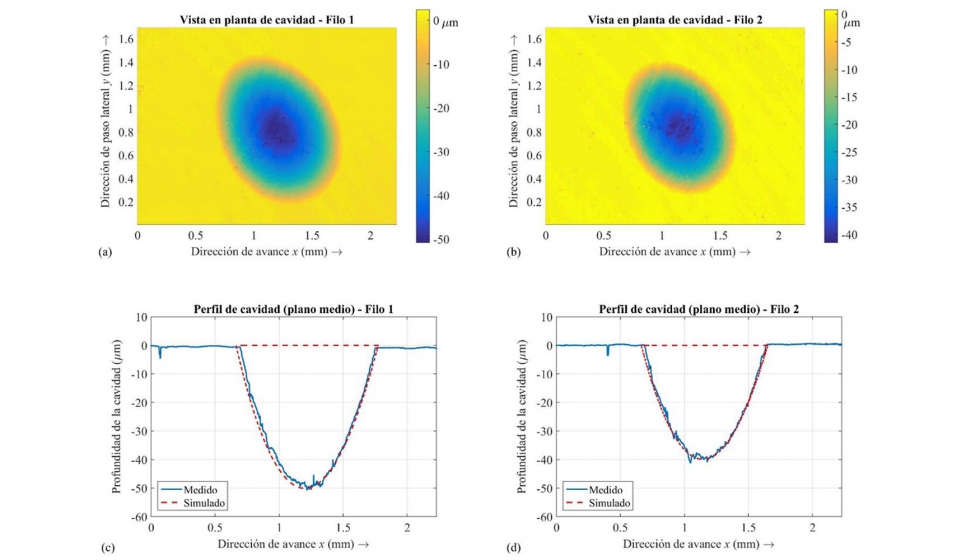
Debido a la excentricidad radial, la profundidad de las cavidades también es distinta, aproximadamente 50 micras para la cavidad generada por el filo 1 y 40 micras para la generada por el filo 2. En estas figuras, también se representan los perfiles simulados con las condiciones del ensayo 5 (tabla 1), para cada uno de los filos. Se puede observar una buena correspondencia entre los perfiles medidos y los predichos.

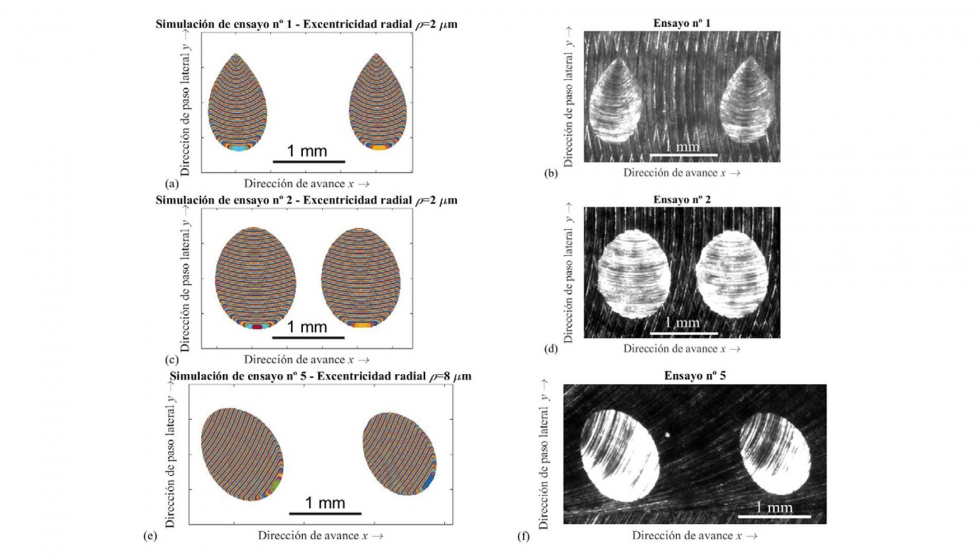
Finalmente, en la figura 11 se compara la geometría de las cavidades simuladas con las obtenidas en los ensayos 1, 2 y 5. En las figuras, se pueden distinguir las marcas dejadas por los filos de corte en su trayectoria. Estas marcas dependen del ángulo de orientación empleado en cada ensayo. Asimismo, se puede apreciar la diferencia en la forma de la cavidad generada en el ensayo 1 con respecto a la obtenida en el resto de ensayos (2 y 5). En los ensayos 2 y 5, la forma de las cavidades se asemeja a elipses mientras que en el ensayo 1, la forma de la cavidad en uno de los extremos es menos redondeada y más puntiaguda. Este cambio en la forma se puede visualizar en la figura 4b cuando el ángulo de inclinación ß es 20º y el de orientación ?, 90º. En cuanto a la orientación ? de las cavidades, se puede observar que en los ensayos 1 y 2, con ?= 90º, la dirección del semieje mayor de la cavidad forma 90º con respecto a la dirección de avance x, mientras que en el ensayo 5, el ángulo ? es 122.6º.

Se ha desarrollado un modelo que permite predecir la geometría de cavidades con forma elíptica generadas en la superficie de piezas fresadas en cinco ejes. El modelo desarrollado en este trabajo tiene en cuenta la excentricidad radial del eje de la fresa respecto al eje de giro del husillo. Debido a que los filos de corte giran respecto al eje del husillo, la excentricidad provoca que cada uno de los filos deje una huella distinta en la superficie fresada. Cuanto mayor es la excentricidad radial, mayor es la diferencia entre las cavidades generadas por cada filo. Con el fin de evitar estas diferencias, se debería emplear portaherramientas que minimicen la excentricidad radial de la fresa.

Se ha analizado la influencia de las condiciones de corte en fresado de cinco ejes (inclinación y orientación de la fresa, avance por filo, profundidad de pasada) y del radio nominal de la fresa en la geometría (forma, dimensiones, orientación, área y densidad superficial) de las cavidades. Se ha comprobado que:

• El ángulo de orientación ? de la fresa con respecto a la dirección de avance influye de manera significativa en la orientación ? de las cavidades generadas.
• El ángulo de inclinación ß del eje del husillo influye en la forma de las cavidades. Para valores de inclinación ß situados entre 30º y 60º, las cavidades tienen forma elíptica mientras que para valores menores a 30º, tienen formas más irregulares.
• A medida que aumenta el avance por filo f_Z, las cavidades tienden a ser más ovaladas de forma que el cociente a/b entre el semieje mayor a y el semieje menor b de las cavidades crece.
• Para los valores más habituales de profundidad de cavidad a_P, la forma y la orientación ? de las cavidades se mantiene constante.

Este análisis ha permitido desarrollar un procedimiento que permite definir las condiciones de fresado necesarias para texturizar una superficie con la cavidad deseada. Dada una profundidad de cavidad a_P, el procedimiento consiste en determinar: 1º) el ángulo de inclinación ß que asegure una forma elíptica, 2º) el ángulo de orientación ? que genere cavidades con una determinada orientación ? y 3º) la combinación entre radio de fresa R y avance por filo f_Z, que garantice un área A y una densidad S de cavidades de profundidad a_P en la superficie de la pieza.

Por último, se ha validado experimentalmente el modelo por medio de la comparación de cavidades simuladas con cavidades generadas en ensayos de fresado de cinco ejes. Para ello, se han comparado la forma, las dimensiones y profundidad de las cavidades y se ha observado una buena correspondencia entre las cavidades predichas y medidas.

Agradecimientos

Los autores agradecen al Ministerio de Economía y Competitividad la financiación del proyecto Turbo (DPI2013-46164-C2-2-R), gracias a la cual se ha realizado este trabajo.

Referencias

[1] A. A. G. Bruzzone, H. L. Costa, P. M. Lonardo, D. A. Lucca, Advances in engineered surfaces for functional performance, CIRP Annals-Manufacturing Technology 57 (2008) 750-769.

[2] D. G. Coblas, A. Fatu, A. Maoui and M. Hajjam, Manufacturing textured surfaces: State of art and recent developments, Proc I. Mech. E. Part J: J Engineering Tribology 2015, Vol. 229(1) 3–29.

[3] A. Arslan, H. H. Masjuki, M. A. Kalam, M. Varman, R. A. Mufti, M. H. Mosarof, L. S. Khuong, M. M. Quazi (2016): Surface Texture Manufacturing Techniques and Tribological Effect of Surface Texturing on Cutting Tool Performance: A Review, Critical Reviews in Solid State and Materials Sciences, DOI: 10.1080/10408436.2016.1186597.

[4] T. Ibatan, M.S. Uddin, M.A.K. Chowdhury, Recent development on surface texturing in enhancing tribological performance of bearing sliders, Surface & Coatings Technology 272 (2015) 102–120.

[5] Y. Qiu, M. M. Khonsari, Experimental investigation of tribological performance of laser textured stainless steel rings, Tribology International 44 (2011) 635–644.

[6] S. Wos, W. Koszela, P. Pawlus, The effect of both surfaces textured on improvement of tribological properties of sliding elements, Tribology International 113 (2017) 182–188.

[7] L. Galda, J. Sep, S. Prucnal, The effect of dimples geometry in the sliding surface on the tribological properties under starved lubrication conditions, Tribology International 99 (2016) 77–84.

[8] A. Greco, S. Raphaelson, K. Ehmann, Q. J. Wang, and C. Lin, Surface texturing of tribological interfaces using the vibromechanical texturing method, J. Manufact. Sci. Eng. 131(6), 061005 (2009).

[9] P. Guo, K. F. Ehmann, An analysis of the surface generation mechanics of the elliptical vibration texturing process, Int. J. Mach. Tools Manuf. 64 (2013) 85–95.

[10] C. Zhang, G. Shi, K. F. Ehmann, Investigation of hybrid micro-texture fabrication in elliptical vibration assisted cutting, International Journal of Machine Tools & Manufacture 120 (2017) 72–84.

[11] E. Graham, C. I. Park, and S. S. Park, Fabrication of Micro-Dimpled Surfaces through Micro Ball End Milling, Int. J. of Precision Engineering and Manufacturing, Sept. 2013, Vol.14, No. 9, pp. 1637-1646.

[12] E. Graham, C. I. Park, S. S. Park, Force modeling and applications of inclined ball end milling of micro-dimpled surfaces, Int. J. Adv. Manuf. Technol. (2014) 70:689–700.

[13] T. Matsumura, S. Takahashi, Micro dimple milling on cylinder surfaces. Journal of Manufacturing Processes 14 (2012) 135–140.

[14] A. Zabel, T. Surmann, A. Peuker, Surface Structuring and Tool Path Planning for Efficient Milling of Dies, Seventh International Conference on High Speed Machining 2008, p. 155-160.

[15] J. Resendiz, E. Graham, P. Egberts, S. S. Park, Directional friction surfaces through asymmetrically shaped dimpled surfaces patterned using inclined flat end milling, Tribology International 91 (2015) 67–73.

[16] M. Arizmendi, M. Artano, A. Jiménez, Generación de texturas superficiales por fresado en cinco ejes, XXI Congreso Nacional de Ingeniería Mecánica, Elche 2016.