Optimización topográfica del suelo para ahorrar agua en el riego superficial


Introducción y objetivos
Con diferencia, el regadío es el mayor consumidor de agua en España. Entre los diversos sistemas de riego (superficial, aspersión y goteo), el riego superficial destaca por su importante consumo de agua, tanto por la gran cantidad de hectáreas de cultivo que representa como por la ineficiencia asociada a este sistema de riego.
En el riego superficial, la principal pérdida de agua a nivel de parcela es la percolación profunda (y la escorrentía superficial si el final del campo es abierto). En general, el riego superficial no es uniforme porque las zonas más cercanas a los puntos de entrada de agua reciben más aportación de agua. En cualquier variante del riego superficial (tablar o surco, con final abierto o cerrado), la uniformidad de distribución es generalmente menor que en los sistemas de riego a presión (aspersión, goteo) (FAO, 2002; Walker y Skogerboe, 1987). La creciente necesidad de ahorrar agua (cambio climático, superpoblación) y las modernas técnicas disponibles de nivelación de parcelas de riego (láser, GPS) justifican el estudio de la influencia de la forma de la superficie campo en la uniformidad del riego superficial (Playán et al., 1996).
Para evitar en la medida de lo posible la pérdida de agua por percolación profunda y por escorrentía superficial, este estudio presenta y aplica una nueva metodología que permite encontrar la mejor forma topográfica del suelo para ayudar al agua a distribuirse uniformemente por el campo, en función de los parámetros de infiltración, el coeficiente de rugosidad de Manning, el caudal de riego, la geometría del campo y la dosis de riego.

Materiales y métodos
Para alcanzar el objetivo planteado, se ha desarrollado una nueva metodología con el fin de encontrar una forma de la superficie del suelo teóricamente perfecta en cada caso en particular. Esta metodología, a través de un proceso iterativo, conduce a un perfil de superficie de suelo curvo que obtiene teóricamente una uniformidad de distribución (DU, distribution uniformity) del 100% sin percolación profunda en cualquier variante de riego superficial.
Para la aplicación del método, es necesaria la utilización de un modelo informático de simulación hidráulica del riego superficial. En cada iteración del método, se eleva topográficamente la parte del campo que ha recibido más agua en la simulación anterior, y se baja topográficamente la parte del campo que ha recibido menos agua en la simulación anterior. Hechas ambas modificaciones del perfil del suelo, se realiza una nueva simulación hidráulica ajustando el tiempo de riego para que la infiltración mínima (zmin) coincida con la infiltración requerida o dosis de riego (zreq). La repetición iterativa de estas operaciones conduce a una evolución de la forma del perfil del suelo hasta conseguir una uniformidad de distribución del agua teóricamente perfecta.
Resultados
Se analiza el caso de un campo de riego superficial con final cerrado, extraído de Dholakia et al. (1998). El campo tiene una longitud de 185,9 metros y se riega con un caudal de 10,93 litros por segundo por metro de ancho. La dosis de riego es de 100 milímetros y el coeficiente de Manning es de 0,10 s/m1/3. La cantidad de agua que se infiltra en el suelo en relación con el tiempo se puede representar mediante la siguiente función de infiltración:
z(mm)=73,72•t(h)0,6
La aplicación del método de optimización topográfica descrito anteriormente hace “evolucionar” teóricamente el suelo del campo hacia formas cada vez más eficientes. Se ha realizado un video que muestra esta evolución a lo largo del proceso iterativo, partiendo del suelo horizontal y llegando hasta el perfil optimizado. Este vídeo se encuentra disponible en la URL http://www.youtube.com/watch?v=mNozM1rTDMk.
La figura 1 muestra los resultados obtenidos mediante tres gráficos diferentes: el primero de ellos muestra la evolución de la uniformidad de distribución (DUabs), el tiempo de corte (el tiempo de aplicación del agua, cutoff time, Tco) y la percolación profunda (DP, deep percolation) a lo largo del proceso iterativo de la metodología; el segundo gráfico muestra el diagrama de avance y receso para las situaciones inicial y final del proceso; el tercer gráfico muestra la forma final del campo optimizado topográficamente, así como el proceso de infiltración del agua de riego con el perfil optimizado, junto con la infiltración final del campo sin pendiente.
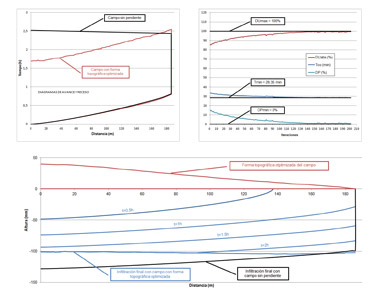
Nótese el paralelismo existente entre la curva de avance y la de receso del perfil optimizado. Esto indica que los tiempos de oportunidad (los tiempos durante los cuales hay infiltración) de todos los puntos del campo son similares. Ello conduce al perfil final de infiltración prácticamente horizontal y coincidente con la dosis de riego que se observa en el tercer gráfico de la figura 1. El riego ha sido teóricamente perfecto, con una uniformidad de distribución del 99,4%.
En la tabla 1 se muestra cómo se modifican DU, DP, el tiempo de riego y el volumen de agua de riego entre las situaciones inicial (campo sin pendiente) y final (campo con forma topográfica optimizada).

La última columna de la tabla ilustra el ahorro del 13,1% de agua y de tiempo de riego que se alcanza en el caso estudiado, debido a la eliminación de la percolación profunda.
Discusión y conclusiones
La metodología presentada ofrece como resultado una forma topográfica curva del campo. Resulta técnicamente más complejo dotar a un campo de una forma curva que de una forma plana (con o sin pendiente). Por ello, la forma óptima que se obtiene podría ser útil a la hora de decidir la pendiente única o el conjunto de pendientes del campo, para proceder a su conformación mediante técnicas láser o GPS.
Desde un punto de vista estrictamente teórico, la principal conclusión es que el método consigue un riego superficial uniforme optimizando la forma del campo.
Desde un punto de vista práctico, se puede añadir que los resultados pueden ser útiles cuando la disponibilidad de agua es un factor limitante, porque podría lograrse un ahorro de agua sustancial en tales casos a través de la conformación cuidadosa de la topografía de los campos de riego. En otros casos, los resultados pueden servir de guía para decidir una pendiente apropiada para el campo, o un conjunto de dos o tres pendientes que acerquen la forma topográfica del campo a su forma topográfica óptima.
Referencias
Dholakia, M., Misra R., Zaman, M.S. 1998. Simulation of border irrigation system using explicit MacCormack finite difference method. Agricultural Water Management 36, 181-200.
FAO. 2002. Irrigation manual – planning, development, monitoring and evaluation of irrigated agriculture with farmer participation. Food and Agriculture Organization of the United Nations. Harare, Zimbabwe.
Playán, E., Faci, J. M., and Serreta, A. 1996. Characterizing microtopographical effects on level-basin irrigation performance. Agricultural Water Management 29, 129-145.
Walker, W. R. y Skogerboe, G. V. 1987. Surface irrigation. Theory and practice. Prentice-Hall, Englewood Cliffs, N.J., EE UU.