Efecto materno y edad en la madre en vacuno de carne en la Raza Pirenaica
Anna Ruzzon, David López-Carbonell, Juan Altarriba, Carlos Hervás-Rivero, Houssemeddine Srihi, Luis Varona.
Grupo de Genética Cuantitativa y Mejora Animal. Universidad de Zaragoza. Instituto Agroalimentario de Aragón (IA2). 50013. Zaragoza.
04/12/2023Los programas de mejora genética de vacuno de carne definen habitualmente un índice compuesto para carne y otro para vida. El índice compuesto para carne se centra en los caracteres de crecimiento y conformación ya que su objetivo es detectar a los mejores reproductores para enviar sus descendientes al sacrificio, bien en raza pura o en cruce industrial. Por otra parte, el índice compuesto para vida pretende identificar aquellos machos y hembras cuyo destino reproductivo es proporcionar a los futuros reproductores de la raza. Entre los caracteres incluidos en los índices para vida cobran importancia los caracteres relacionados con la reproducción y las características maternas de las hembras que incluyen la capacidad lechera y los cuidados en las primeras fases de vida de los terneros.
El peso de los terneros en las primeras fases de vida se ve afectado por dos efectos de origen genético: el efecto atribuible a su propio genoma o efecto genético directo y el efecto atribuible al genoma de su madre o efecto genético materno (Willham, 1963; Koch, 1972). La predicción del mérito genético para estas características maternas se realiza mediante el siguiente modelo lineal (Crews and Wang, 2007):
y=Xb+Zu+Wm+Tp+e
donde y es el vector de datos fenotípicos (peso al destete, peso a los 90 o 120 días), b es el vector de efectos fijos (sexo, edad de la madre, rebaño-año-estación, etc), u es el vector de efectos genéticos directo, m es el vector de efectos genéticos materno, p es el vector de efectos permanentes maternos y e es el vector de residuos. Además, X, Z, W y T son las correspondientes matrices de incidencia que relacionan los datos fenotípicos con b, u, m y p, respectivamente. La implementación de este modelo permite estimar la variabilidad genética que tiene como origen la variabilidad en la configuración genética de los terneros (σ_u^2) o varianza genética directa, y la variabilidad genética atribuible a la variabilidad en configuración genética de las madres (σ_m^2) o varianza genética materna.

Sin embargo, este modelo postula que los efectos maternos tanto genéticos como ambientales ejercen un efecto constante a lo largo de la vida productiva de la vaca. Sin embargo, es razonable pensar que la influencia de las madres en el crecimiento de los tenernos se modifique en función de la edad de las mismas, ya que no todas las madres tienen el mismo patrón de producción de leche a lo largo de su vida. Algunas vacas pueden tener un buen nivel de producción de leche cuando son jóvenes y sufrir una importante reducción al envejecer, mientras que otras pueden mantener la producción de leche en abundancia hasta que son más mayores. Además, este patrón puede tener causas genéticas.
Por este motivo, el objetivo de este trabajo es describir un procedimiento que permita valorar la evolución del efecto genético materno a lo largo de la vida productiva del animal. Para ello, se ha utilizado una base de datos del carácter peso a los 90 días de la raza vacuno Pirenaica. En concreto se dispone de 58,158 pesos entre los 46 y los 135 días con una media de 134,9 kg. y una desviación típica de 39,3 kg.
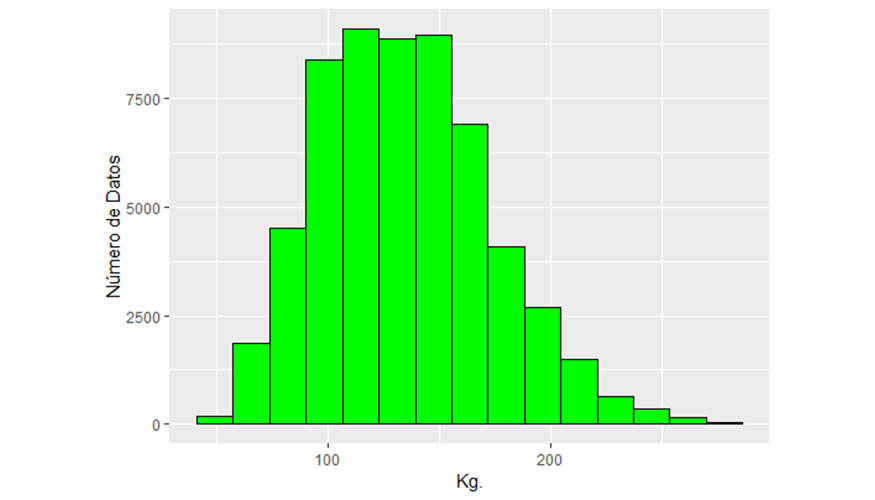
Se seleccionaron aquellos datos procedentes de madres entre los 600 y 6000 días. La edad media de las madres fue de 2.606,96 días (7,14 años) y su desviación típica fue de 1297,87 días (3,56 años). La distribución de las edades de las madres en años se presenta en la Figura 2.
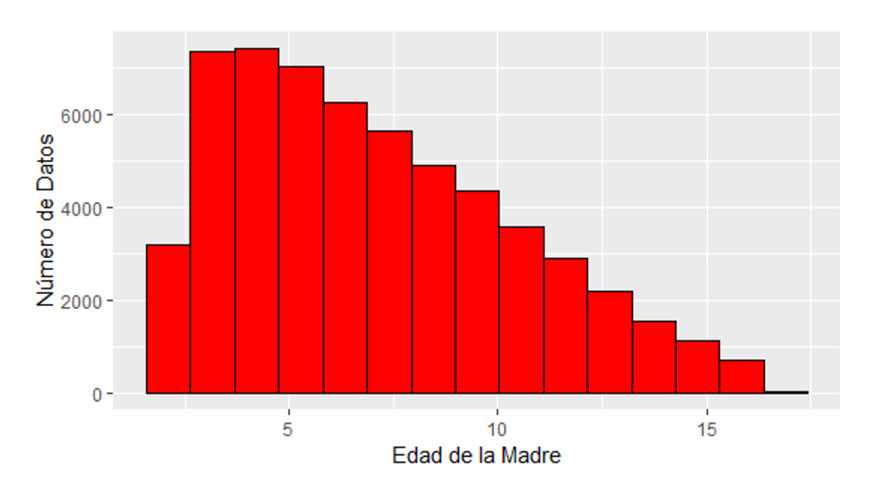
El análisis propuesto utiliza modelos de regresión aleatoria (Schaeffer, 2004; Oliveira et al., 2019), y postula que el efecto de la edad de la madre, el efecto genético materno y el efecto permanente materno están asociados a una trayectoria definida por cinco polinomios ortogonales de Legendre. El modelo estadístico es:
y=Xb+w'r+Z_1 h+Z_2 p+Z_3 m+Z_4 u+e
donde y es el vector de datos fenotípicos, b es el vector de efectos sistemáticos que incluye la edad del ternero y el efecto sexo, r es un vector de coeficientes de regresión asociados con cada polinomio ortogonal, h es un vector de efectos del rebaño-año-estación (9,689 niveles), p es un vector de coeficientes de regresión aleatoria para los efectos permanentes maternos (21.673 niveles x 5 polinomios ortogonales), m es un vector de coeficientes de regresión aleatoria para los efectos genéticos maternos (85.670 niveles x 5 polinomios ortogonales), u es un vector de efectos genéticos aditivos directos (85.670 niveles) y e es el vector de residuos. Además, X, w’, Z1, Z2, Z3 y Z4 son las correspondientes matrices y vectores de incidencia.
La estimación de componentes de varianza y estimación de los efectos genéticos y ambientales se realizó mediante el procedimiento aireml (Gilmour et al., 1995) y utilizando el programa blupf90+ (Misztal et al., 2018). Los resultados de los componentes de varianza y de los efectos genéticos y ambientales para los coeficientes de regresión aleatoria se han utilizado para obtener los siguientes resultados.
En la Figura 3 se presenta la evolución del efecto de edad de la madre en el peso de los terneros a los 90 días.
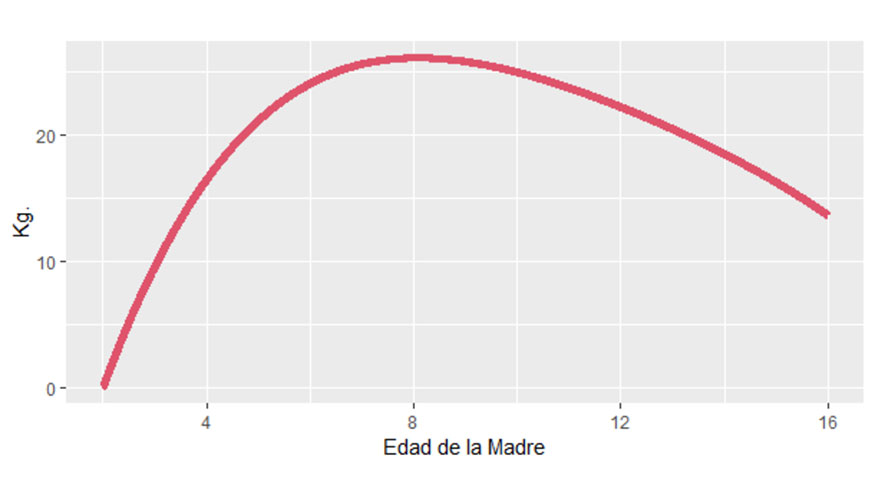
La Figura 3 revela que el efecto de la edad de la madre es menor en hembras muy jóvenes y aumenta rápidamente hasta alcanzar un máximo alrededor de los 8 años, seguido de una disminución gradual. Los resultados de nuestro estudio se alinean con estudios previos en el campo (Gregory et al., 1978; Morales et al., 2013) y con las estimaciones de la evolución de la producción de leche a lo largo de la vida de las vacas (Lubritz et al., 1989; Williams et al., 2022).
A partir de las estimaciones de los componentes de varianza asociados a los polinomios ortogonales, la varianza genética directa y la varianza residual se ha calculado la evolución de la evolución de la heredabilidad directa (atribuible al ternero) y materna (atribuible a la madre) que se presentan en la Figura 4.
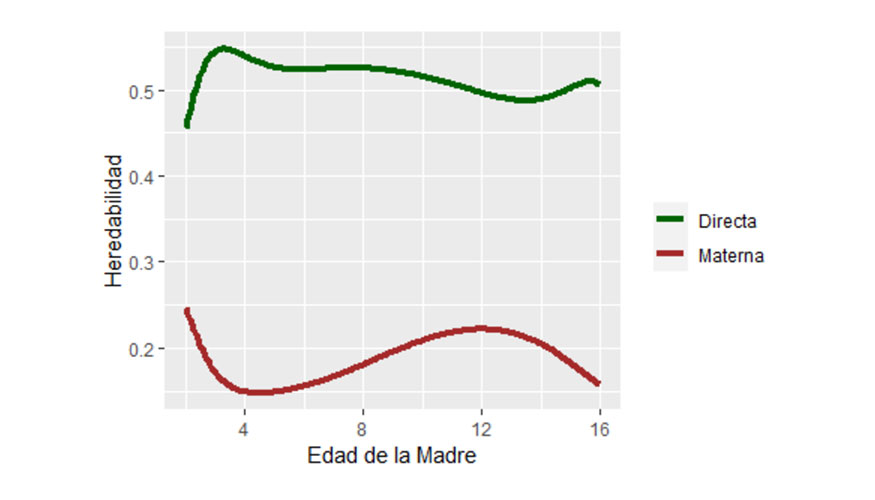
La heredabilidad materna promedio fue de alrededor de 0,20, y osciló entre 0,15 a 0,25 con un aumento constante entre 4,5 a 13 años aproximadamente. Estas estimaciones fueron consistentes con los resultados de estudios previos en ganado vacuno (Meyer, 1992; Gutiérrez et al., 2007). La Figura 5 también presenta la evolución de la heredabilidad directa que sigue un patrón complementario y fluctúa entre 0,45 a 0,55, en el rango superior de estimaciones previas de heredabilidad directa para peso al destete (Utrera and Van Vleck, 2004).
Además, y a partir de estos mismos componentes de la varianza se pueden calcular las correlaciones genéticas entre los efectos maternos asociados con distintas edades de la madre que se presentan en la Tabla 1.
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | |
| 2 | 1 | 0,740 | 0,580 | 0,598 | 0,610 | 0,579 | 0,564 | 0,727 |
| 4 | 1 | 0,958 | 0,907 | 0,858 | 0,823 | 0,808 | 0,789 | |
| 6 | 1 | 0,974 | 0,924 | 0,878 | 0,838 | 0,755 | ||
| 8 | 1 | 0,982 | 0,938 | 0,883 | 0,791 | |||
| 10 | 1 | 0,981 | 0,934 | 0,827 | ||||
| 12 | 1 | 0,982 | 0,852 | |||||
| 14 | 1 | 0,894 | ||||||
| 16 | 1 |
En la tabla se observa que las correlaciones adyacentes son más elevadas y cercanas a la correlación total (1.00). Sin embargo, las correlaciones se reducen a medida que hay más diferencia en las edades y, por otra parte, es destacable que la correlación entre los efectos maternos a edades muy tempranas (2 años) y edades posteriores es más baja (0.5-0.7 aprox.). Este resultado indica que los genes implicados en la variabilidad genética en el efecto materno cuando las vacas son muy jóvenes son parcialmente distintos que los genes que regulan los efectos maternos a edades más avanzadas, ya que el estado fisiológico de los animales es distinto.
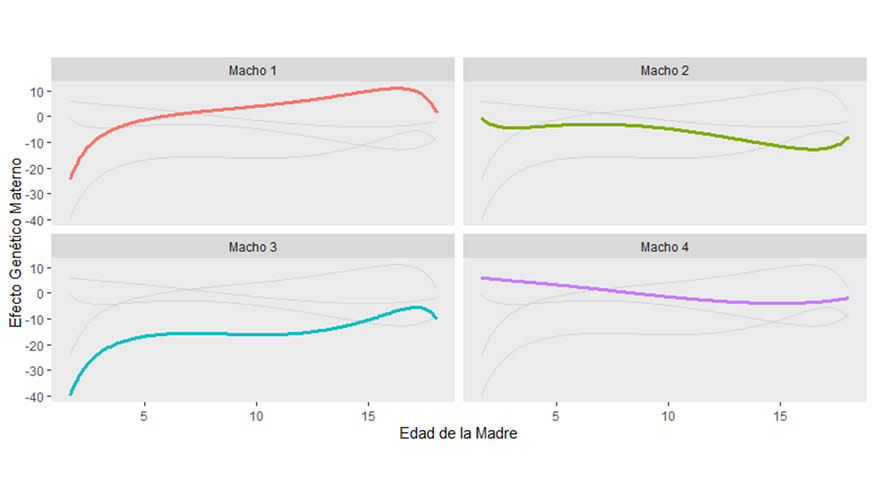
A nivel práctico, la consecuencia más importante de este trabajo es que los valores genéticos para el efecto materno pueden variar a lo largo de la vida productiva de las vacas. En este sentido, la Figura 5 presenta la predicción del mérito genético materno para cuatro machos específicos.
Referencias bibliográficas
- Crews DH and Wang Z 2007. Illustration of the maternal animal model used for genetic evaluation of beef cattle. Journal of Animal Science 85, 1842–1848.
- Gilmour AR, Thompson R and Cullis BR 1995. Average Information REML: An Efficient Algorithm for Variance Parameter Estimation in Linear Mixed Models. Biometrics 51, 1440.
- Gregory KE, Cundiff L V., Koch RM, Laster DB and Smith GM 1978. Heterosis and Breed Maternal and Transmitted Effects in Beef Cattle I. Preweaning Traits2,3,7. Journal of Animal Science 47.
- Gutiérrez JP, Goyache F, Fernández I, Alvarez I and Royo LJ 2007. Genetic relationships among calving ease, calving interval, birth weight and weaning weight in the Asturiana de los Valles beef cattle breed. Journal of Animal Science 85.
- Koch RM 1972. The role of maternal effects in animal breeding. VI. Maternal effects in beef cattle. Journal of animal science 35, 1316–1323.
- Lubritz DL, Forrest K and Robison OW 1989. Age of cow and age of dam effects on milk production of Hereford cows. Journal of animal science 67, 2544–2549.
- Meyer K 1992. Variance components due to direct and maternal effects for growth traits of Australian beef cattle. Livestock Production Science 31, 179–204.
- Misztal I, Tsuruta S, Lourenco D, Aguilar I, Legarra A and Vitezica Z 2018. Manual for BLUPF90 family of programs. University of Georgia, Athens, GA (USA).
- Morales R, Menéndez-Buxadera A, Avilés C and Molina A 2013. Direct and maternal genetic effects for preweaning growth in Retinta cattle estimated by a longitudinal approach throughout the calving trajectory of the cow. Journal of Animal Breeding and Genetics 130, 425–434.
- Oliveira HR, Brito LF, Lourenco DAL, Silva FF, Jamrozik J, Schaeffer LR and Schenkel FS 2019. Invited review: Advances and applications of random regression models: From quantitative genetics to genomics. Journal of Dairy Science 102, 7664–7683.
- Schaeffer LR 2004. Application of random regression models in animal breeding. Livestock Production Science 86, 35–45.
- Utrera AR and Van Vleck LD 2004. Heritability estimates for carcass traits of cattle: a review. Genetics and molecular research : GMR 3, 380–394.
- Willham RL 1963. The Covariance between Relatives for Characters Composed of Components Contributed by Related Individuals. Biometrics 19, 18.
- Williams M, Sleator RD, Murphy CP, McCarthy J and Berry DP 2022. Exploiting genetic variability in the trajectory of lactation yield and somatic cell score with each progressing parity. Journal of Dairy Science 105.






