¡Ponga un modelo en el taller!
Tendencias en modelización de los procesos de mecanizado
En sectores como el aeronáutico, aeroespacial, eólico o médico, generar un producto final de alta calidad y a la primera es fundamental. Para ello, es necesario utilizar técnicas avanzadas de diseño, modelos predictivos del proceso de corte, así como técnicas de monitorización online para detección y corrección de errores que ayuden a obtener una producción estable y libre de defectos. A continuación se presenta una visión global de las necesidades y tendencias actuales relacionadas con la simulación, desde la modelización necesaria en la propia concepción de las máquinas-herramienta hasta la modelización de los procesos de mecanizado.
Durante las últimas décadas ha habido un progreso significativo en el desarrollo de modelos predictivos para la predicción de las operaciones de mecanizado y poder hacer frente a los nuevos avances en tecnologías de máquinas-herramienta, herramientas de corte y desarrollo de materiales avanzados, todos ellos orientados a mejorar la productividad de los procesos de fabricación, la calidad del producto y la reducción de costes. Sin embargo, la adopción de estos modelos por la industria depende de la capacidad de los mismos para predecir el rendimiento de mecanizado, obteniendo resultados de estabilidad del proceso, fuerzas de corte, potencia y par de corte, formación de viruta, desgaste de herramientas, integridad superficial y precisión de las piezas obtenidas.
1. Introducción
La utilización de la modelización para predecir el comportamiento en el mecanizado de un material no es algo nuevo. De hecho, se viene estudiando desde hace muchos años cuando los pioneros Ernst y Merchat realizaron en 1945 los primeros estudios de la mecánica de corte.
En los últimos 50 años, se ha avanzado en esta línea y se han desarrollado diferentes modelos para los procesos de mecanizado, los cuales se pueden clasificar en cinco categorías genéricas: modelos empíricos, analíticos, mecanísticos, numéricos e híbridos [1].
Los modelos empíricos son relaciones entre diferentes variables del proceso obtenidas a partir de ensayos experimentales, obteniendo así ecuaciones de fuerzas de corte, temperaturas de corte, vida de herramienta y rugosidad superficial a partir de variables como material de la pieza, geometría y material de la herramienta y condiciones de corte. Estos modelos suponen un consumo de tiempo y coste muy elevado, más aún cuando en estas ecuaciones es necesario introducir el material de pieza y cuando pequeñas desviaciones en la composición del material causan grandes cambios en las características del mecanizado.
Un enfoque mucho más preciso que los métodos puramente empíricos son los modelos mecanísticos que permiten un cálculo rápido y eficiente de las fuerzas de corte. Este tipo de modelos tienen una parte empírica, ya que emplean unos coeficientes específicos que dependen del binomio de material herramienta-pieza y de la geometría de la herramienta, que normalmente se obtienen a partir de unos ensayos experimentales, y es por ello que a este tipo de modelos también se les conoce como semi-empíricos. Este tipo de modelos se pueden emplear en operaciones complejas de mecanizado, tales como fresado con herramientas de geometría compleja, donde se considera el filo de corte como una sucesión de elementos diferenciales. A cada uno de estos elementos diferenciales se le aplica el modelo propuesto para posteriormente pasar a realizar su integración a lo largo de todo el filo de corte. La integración del modelo diferencial a lo largo del filo se realiza atendiendo a la inmersión de la herramienta en el material, calculada de forma exacta, para obtener las resultantes de la fuerza.
Por otra parte, desde los años 40 se han realizado esfuerzos en estudiar de una forma detallada la denominada mecánica del corte, buscando relacionar la geometría de operaciones sencillas con el comportamiento del material, obteniéndose así valores característicos de la operación como la tensión de cizalladura, el ángulo de cizalladura y el coeficiente de fricción. Actualmente los modelos analíticos, representados por diferentes soluciones de la teoría del plano de cizalladura, pueden predecir directamente las fuerzas de corte, la fricción en las zonas de corte locales, las tensiones, las deformaciones, las tasas de deformación y las temperaturas. Sin embargo, la complejidad de los procesos industriales aún dificulta la predicción de todos los resultados relevantes de la industria de forma analítica. Además, estos modelos analíticos son bastante controvertidos ya que hasta la fecha no existe un modelo universalmente aceptado o empleado.
Dentro de los modelos que estudian la mecánica de corte también destacan los denominados métodos numéricos, que permiten el estudio de campos de tensiones, temperaturas en la zona de corte y deformaciones entre otros. Dentro de los modelos numéricos podemos distinguir tres técnicas diferentes: el Método de Elementos Finitos (MEF), el Método de Diferencias Finitas (MDF) y el Método de Elemento de Frontera (BEM, por sus siglas en inglés).
En los últimos años, el MEF se ha convertido en la principal herramienta para simular los procesos de corte. Se usa para calcular las distribuciones de tensiones, deformaciones, tasas de deformación y temperaturas en las zonas de corte primaria, secundaria y terciaria. Como consecuencia, se pueden obtener las temperaturas en la herramienta, viruta y pieza, así como las fuerzas de corte, deformaciones plásticas (ángulo de cizalladura y espesor de viruta), formación de viruta y su posible rotura de una forma más rápida que usando los costosos y tediosos ensayos experimentales.
Para estos Métodos de Elementos Finitos las aproximaciones típicas son las formulaciones Lagrangiana y Euleriana, así como la combinación de ambas llamada formulación arbitraria Lagrangiana-Euleriana (ALE). La característica principal de la formulación Lagrangiana es el hecho de que la malla está en todo momento fija al material. Esta formulación es la más utilizada para resolver problemas de la mecánica de sólidos, porque las deformaciones que van a sufrir los cuerpos van a ser pequeñas. Sin embargo, este método no es apropiado cuando se producen grandes deformaciones ya que se producen una fuerte distorsión de la malla, lo que amplifica el error numérico y hace que los resultados obtenidos sean incorrectos. La característica fundamental que define al método Euleriano radica en que el mallado permanece fijo en el espacio y es el material el que fluye a través de él. El hecho de que la malla no se deforme es la gran ventaja del método Euleriano frente al Lagrangiano, pues lo hace idóneo para ser aplicado en problemas con grandes deformaciones como impactos de sólidos o interacciones con fluidos. En contra, como punto negativo de este método hay que destacar que a causa de la separación entre el movimiento del material y la malla, el sistema tiene una mayor complejidad y un mayor coste computacional. La formulación arbitraria Lagrangiana-Euleriana (ALE) surge para tratar de sobreponerse a las carencias de los dos métodos anteriores combinando los beneficios de ambos. Esto es, capacidad de simular problemas expuestos a grandes deformaciones con un coste computacional adecuado, siendo por ello muy utilizado para modelizar los procesos de corte.
Entre los mayores inconvenientes que presentan estos modelos numéricos está la dificultad de caracterizar adecuadamente el comportamiento del material a las altas temperaturas y tasas de deformación que se dan en el mecanizado, así como la dificultad de representar adecuadamente el rozamiento que se produce entre la herramienta y pieza. Otra importante desventaja de estos modelos numéricos es su elevado tiempo computacional, sobre todo en aquellos modelos en 3D.
En cuanto a los modelos híbridos, el objetivo de los mismos es combinar las fortalezas de los diferentes modelos. Así, se pueden encontrar, entre otros, modelos analíticos/numéricos o empíricos/numéricos. De esta manera, por ejemplo, esos modelos analíticos proporcionan una entrada útil para optimizar los modelos numéricos, y así ofrecer una predicción realista de resultados relevantes para la industria. Este enfoque híbrido no se ha implementado completamente, pero es probable que sea un objetivo importante de la investigación futura.
2. Modelos para máquinas y procesos
A continuación se presenta una visión global de los modelos que existen actualmente tanto para la optimización del diseño de las máquinas-herramientas como los procesos de mecanizado. En la figura 1 se muestra un esquema que resume quién o quiénes pueden ser un usuario de estos modelos, qué y para qué se utilizan las diferentes técnicas de simulación y finalmente se muestras algunos software comerciales que aplican dichas técnicas.
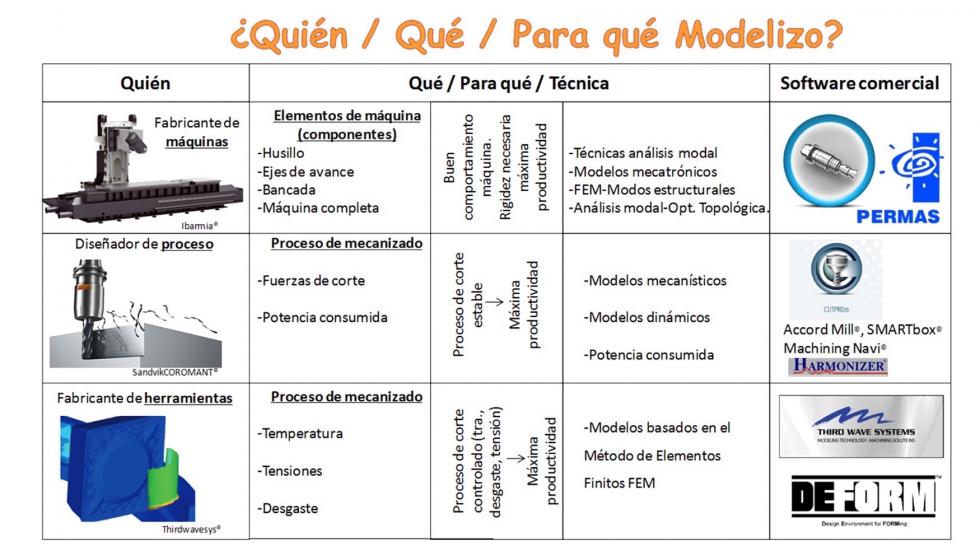
2.1. Modelización componentes máquina
- Máquina-herramienta: caracterización y optimización topológica
Los fabricantes de máquina-herramienta buscan el diseño de máquinas robustas para resistir con facilidad las tensiones generadas durante el proceso de corte así como las cargas térmicas, que deben ser derivadas para evitar puntos calientes. Todo ello debe realizarse gastando la mínima cantidad de material y energía posible. Estos objetivos son en sí contradictorios ya que para buscar robustez, rigidez y aumento de inercia térmica se tiende a incrementar la masa de la máquina incrementándose así el consumo de energía de la máquina. Por tanto, buscar un compromiso entre todas estas variables constituye un reto.
En los últimos años, la sostenibilidad ambiental ha ganado un interés cada vez mayor entre las capacidades exigibles a una máquina. Esto influye no sólo en economía de costes y en la fabricación de un producto competitivo sino en una mejor imagen de la empresa por parte de clientes y sociedad. Por ello, muchas empresas llevan a cabos modelos macroscópicos que permitan visualizar y reducir el impacto de sus máquinas. Así, estudios realizados por el centro tecnológico Tecnalia y la universidad del País Vasco (UPV/EHU) sobre una máquina fresadora estándar dieron como resultado que el período de uso de la maquina afecta en el 90% del impacto total. La figura 2 muestra los resultados del mencionado estudio de ciclo de vida o LCA (Life Cycle Assessment): una gran parte de la energía consumida en el período de uso, sobre el 50% para un gran grupo de máquinas-herramienta, se asocia con los elementos móviles de la estructura.
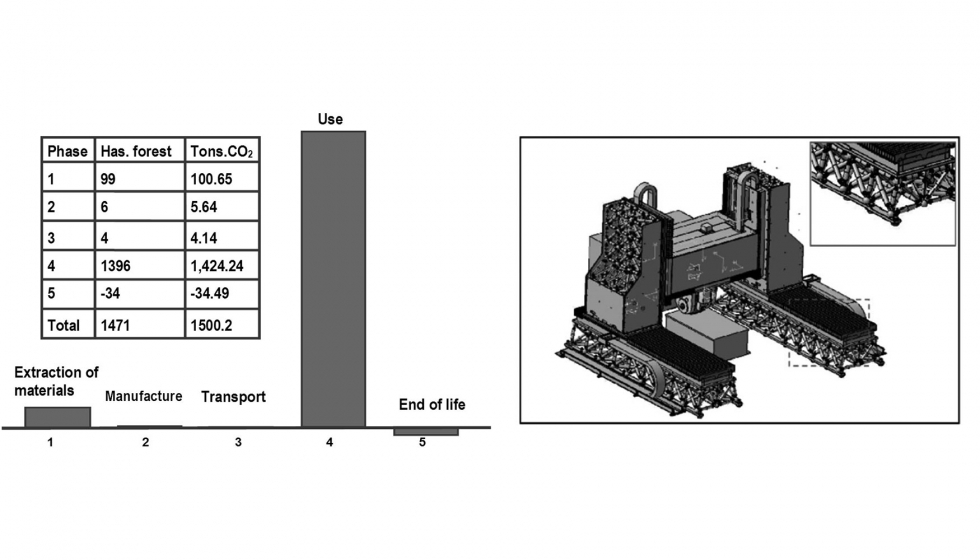
La realidad hoy día es que modelos verdaderamente completos de máquina-herramienta resultan costosos de ejecutar y muy difíciles de poner a punto (ajustar) al involucrar gran cantidad de detalles del diseño mecánico: valores de rigidez de los rodamientos (tolerancias de ensamblaje), amortiguamiento (diferentes mecanismos de disipación del calor y localizaciones), influencias de los elementos removibles (cómo afectan portaherramientas de diferentes diámetros y voladizos sobre los aspectos anteriores).
Existe no obstante una búsqueda o preocupación en la optimización de morfologías de máquina-herramienta o en su redefinición. Para ello, el uso de programas basados en elementos finitos (FEM) es muy común. Hoy día, existen algunas plataformas comerciales con algoritmos llamados de optimización topológica. Por ejemplo, la Universidad de Stuttgart ofrece el programa PERMAS [2] para análisis de componentes mecánicos de cierta complejidad. La técnica consiste básicamente en eliminar material de una estructura-máquina de partida hasta que ya no es posible continuar sin deteriorar las propiedades estáticas y dinámicas de la máquina. Además, esos programas deben proporcionar también una solución viable desde el punto de vista del coste de fabricación.
![Figura 3. Paquete comercial PERMAS para modelización de elementos básicos de máquina-herramienta [2] Figura 3. Paquete comercial PERMAS para modelización de elementos básicos de máquina-herramienta [2]](https://img.interempresas.net/fotos/1459703.jpeg)
Puesto que el descenso de rigidez lleva consigo la redefinición de valores umbrales de rigidez, estática y dinámica, deben identificarse los modos estructurales más restrictivos. Para ello, se lleva a cabo la caracterización modal de la máquina mediante ensayos de impacto con martillo instrumentado. La idea es identificar los modos estructurales de la máquina desnuda, sin portaherramientas, piezas ni amarres. De esta forma la propia empresa es capaz de corroborar o retroalimentar los valores del modelo FEM de la máquina, principalmente, en lo que tiene que ver con las uniones entre elementos fijos y móviles. En máquinas grandes, deberá seleccionarse una pauta adecuada de selección de puntos en todo el rango de trabajo posible de la máquina. Por ejemplo, la figura muestra el rango de variación de los modos de flexión para distintas posiciones del plato. En este caso, el plato divisor contiene el movimiento Y transversal de la pieza.
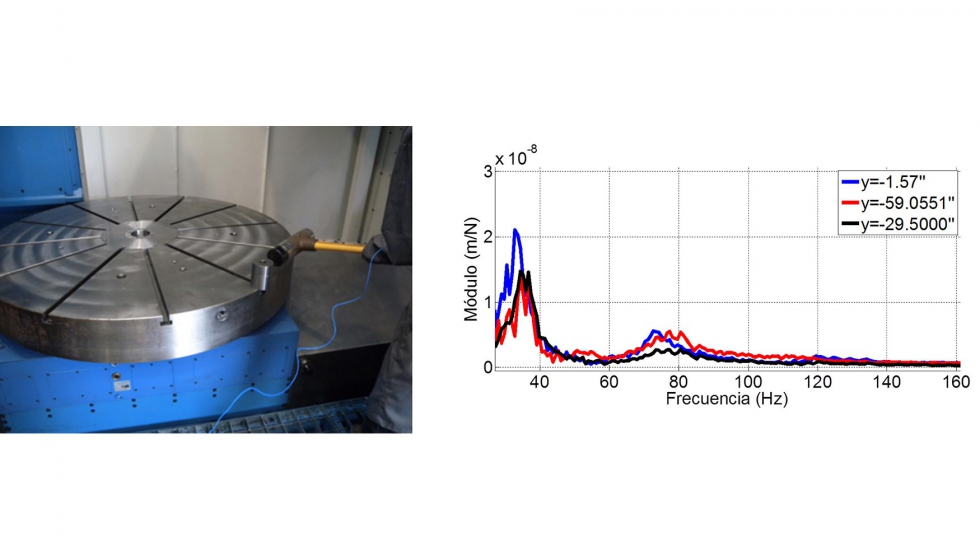
En este sentido los diagramas de lóbulos son una buena manera de evaluar la productividad de diferentes arquitecturas, ya que proporcionan la profundidad de corte en función de la velocidad de giro del cabezal. Estos lóbulos son función de múltiples factores como: material pieza, rigidez dinámica en punta de herramienta, geometría de herramienta, inmersión radial, tipo de amarres, etc. Introduciendo estos datos junto a las características modales de la máquina, puede tenerse una idea de las profundidades de corte alcanzables por la máquina.
- Husillo principal
El cabezal principal representa el corazón de la máquina: debe reunir condiciones de potencia y velocidad junto con altas prestaciones de concentricidad, coaxialidad y equilibrio de giro. Los modelos normalmente atienden a dos conceptos: modelos mecánicos, para el estudio de la rigidez, y modelos térmicos. Mediante los mismos se trata de obtener un cabezal rígido, robusto y con una conducción adecuada del calor.
Los modelos mecánicos suelen considerar conexiones rígidas entre herramienta-porta-eje husillo modelizándolos como vigas de diferente sección (viga según Timoshenko, por ejemplo). También, modelizan los rodamientos como simples muelles con sus rigideces radial y axial. Estas hipótesis no son del todo correctas. Por ello, se recurre a modelos más complejos y complicados de implementar, que incluyan las fuerzas centrifugas y momentos giroscópicos en los rodamientos.
Nuevamente, los elementos finitos son fundamentales para determinar a priori el futuro comportamiento del cabezal. En la figura 5, se muestra el modelo adoptado por el paquete comercial SpindlePro de la Universidad British Columbia [3]. En él se sigue un modelo de viga de Timshenko, donde los puntos negros representan los nodos del sistema. En cada uno de ellos, se dispone de tres desplazamientos posibles y de dos rotaciones. La polea se modeliza como un disco rígido y el espaciador de los rodamientos como un elemento barra. El husillo tiene dos rodamientos frontales en tándem y otros tres también en tándem atrás. Se asume un cabezal axisimétrico (para considerarlo 2D) con posibilidad de tener en cuenta las deformaciones axiales, flectoras y torsionales del sistema. También se permite la incorporación de rodamientos y otros elementos accesorios sobre el husillo.
A partir del software, se puede analizar la respuesta estática y dinámica del husillo de alta velocidad al realizar modificaciones constructivas o asumir nuevas hipótesis. La figura 5 muestra las respuesta en frecuencia del cabezal (es decir, su incremento teórico de rigidez) tras la optimización. Lógicamente, si el husillo ya está fabricado, se puede optar por la caracterización modal para obtener las FRFs del sistema por vía experimental y comparar si el modelo FEM se ajusta a la realidad.
![Figura 5. Spindle Pro de la UBC: corazón de un modelo FEM posible e interfaz de usuario, y optimización de las prestaciones del husillo [3]... Figura 5. Spindle Pro de la UBC: corazón de un modelo FEM posible e interfaz de usuario, y optimización de las prestaciones del husillo [3]...](https://img.interempresas.net/fotos/1459706.jpeg)
Asimismo, tampoco debe despreciarse en general el error de origen térmico del cabezal. Las principales fuentes de este error vienen de variaciones de temperatura de los motores y de los rodamientos y se han llegado a totalizar entre un 50-80% de los errores totales de origen térmico en una máquina. Mientras que el movimiento de los ejes de avance es pequeño o intermitente, puede considerarse que el cabezal siempre está girando. Los errores debidos a la temperatura se dividen en axiales (ATGE, axial thermal growth error) y radiales (RTDE, radial thermal drift error) al husillo. Para solucionar estos problemas, no sólo existen los ya conocidos modelos térmicos en paquetes comerciales como Abaqus o Ansy©. Modelos de tipo físico pueden predecir las elongaciones o distorsiones térmicas en el husillo una vez conocidas las variaciones de temperatura detectadas por los sensores. Los resultados pueden ser corroborados de forma experimental mediante sensores de desplazamiento [4]. Una vez conocidas estas desviaciones pueden corregirse por compensación.
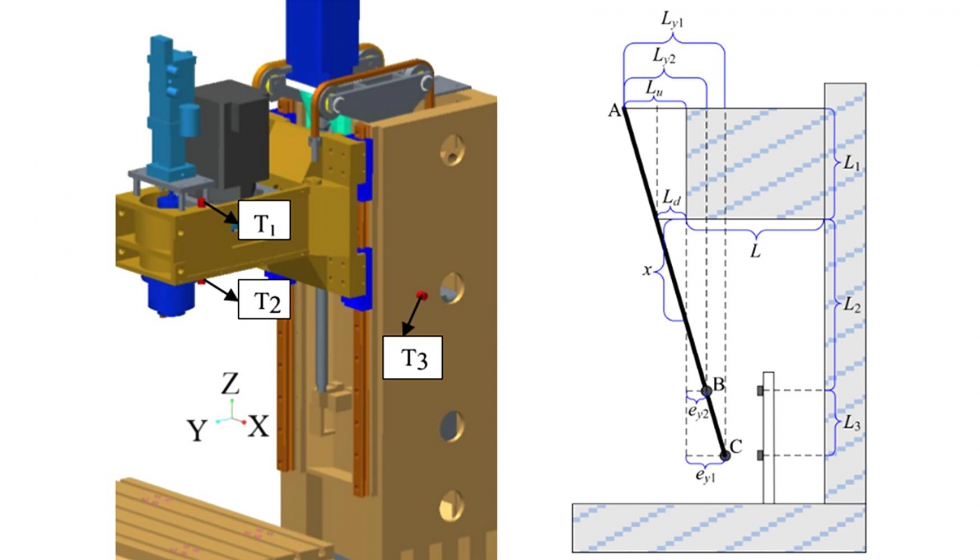
- Modelización conjunto máquina-portaherramientas-herramienta
Ya se ha comentado anteriormente lo interesante que es el ensayo con martillo instrumentado para la obtención de las características dinámicas de un sistema. El inconveniente que presenta es que se requiere un set de mediciones diferente cada vez que se cambie el portaherramientas y/o herramienta sobre el cabezal. Es decir, si existen 25 herramientas en el carrusel de nuestra máquina y suponiendo que los desplazamientos en Z sean despreciables, entonces se requerirá un mínimo de 50 mediciones para los ejes X e Y. Lo mismo ocurrirá si se desea trabajar con una herramienta en concreto pero modificando el portaherramientas.
La aproximación que va ganando terreno en los últimos años es la técnica llamada de acoplamiento de receptancias o RC (Receptance Coupling), donde se trata de modelizar los dos elementos más sencillos, herramienta y porta, mediante modelos de viga sencillos, mientras que el resto, es decir, toda la máquina hasta el cabezal, se obtiene por vía experimental, por ser bastante más problemático de modelizar. Mediante esta técnica de superposición, pueden obtenerse las FRF principales de todas las máquinas de arranque de viruta de un taller quedando almacenadas en una biblioteca de datos. En este caso es recomendable realizar nuevas medidas al de cierto tiempo para reactualizar los datos de la máquina ya que al ser más vieja va a tener mayores holguras. De esta manera, puede incorporarse fácilmente toda una familia de herramientas a usar en una máquina, sin necesidad de nuevas tandas de mediciones experimentales. La figura muestra la plataforma desarrollada por la UPV/EHU para la generación de FRFs de conjuntos máquina-porta-herramienta, basadas en técnicas RC.
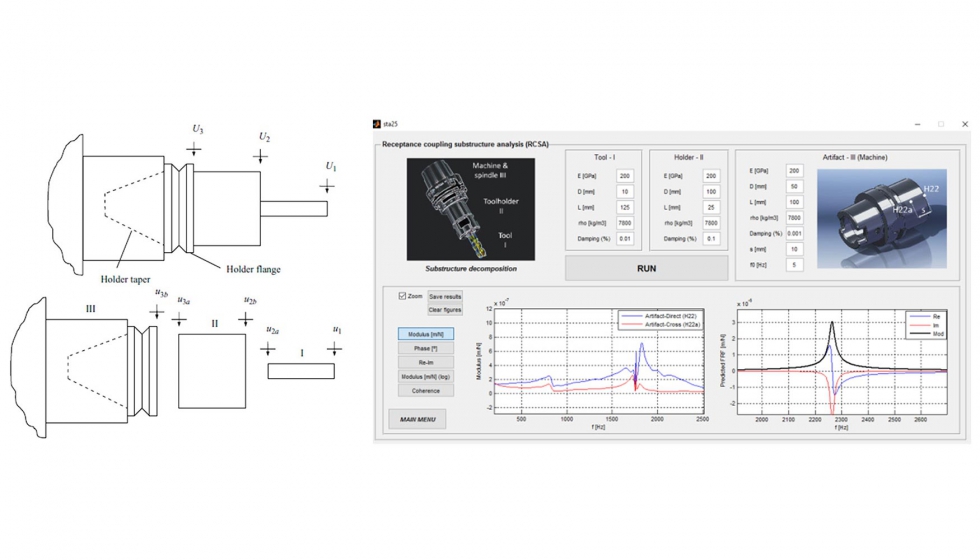
2.2. Desarrollos en el entorno de producción
Todo fabricante, cada vez que diseña una nueva pieza, se enfrenta a un ciclo ‘experiencia-prueba-error’ para resolver aspectos tales como la obtención de las mejores condiciones de corte, determinación de las zonas críticas donde es necesario utilizar avances reducidos, elección de las herramientas que sean capaces de soportar las condiciones de corte establecidas, elección del fluido de corte más adecuado y cálculo de la potencia requerida en la operación entre otros factores.
En estas fases previas a la ejecución del mecanizado, la simulación se presenta como una herramienta útil, permitiendo optimizar el proceso, evitando los costosos ensayos de prueba y error. Esto se traduce en una ahorro de tiempo y recursos y por tanto, en una reducción de costes del proceso productivo.
En cuanto a los modelos empleados para la simulación del proceso de corte, los más utilizados tanto a nivel de investigación como a nivel de aplicación industrial son los basados en modelos mecanísticos, modelos dinámicos y en el método de elementos finitos.
- Modelos mecanísticos y dinámicos
Los modelos mecanísticos permiten calcular las fuerzas de corte de una forma rápida y eficiente, incluso en operaciones complejas como el fresado. El conocimiento de estas fuerzas de corte tiene una gran importancia puesto que influye en aspectos relacionados con la productividad, la estabilidad del proceso y la calidad de los componentes fabricados [6], [7].
Son muchos los autores dedicados al estudio de las fuerzas de corte y al desarrollo de modelos mecanísticos de mecanizado con el objetivo de predecir las fuerzas de corte que tendrán lugar en pos de evitar esfuerzos excesivos o inadecuados que den lugar a errores en el mecanizado. Sin embargo, uno de los mayores retos de los modelos es la transferencia industrial. La mayoría de los desarrollos no llegan a transferirse a la producción debido a la dificultad de generalización de los procesos, variedad de materiales, herramientas, etc. En este sentido, destaca el caso de éxito del software Cutpro desarrollado por MAL (Manufacturing Automation Laboratories). El software está orientado a la obtención de las mayores tasas de arranque de material maximizando la vida de la herramienta y del husillo a través del control de los esfuerzos de corte. El software de uso general abarca procesos de fresado, torneado, mandrinado y taladrado tanto en tres como en cinco ejes y es de aplicación en mecanizados de alta velocidad en materiales ‘blandos’ y en mecanizados de baja velocidad en materiales ‘duros’. Consta de seis módulos diferentes: fresado, torneado/mandrinado, taladrado, análisis modal, medida de la función de transferencia y adquisición de datos.
![Figura 8. Módulos integrados en Cutpro [8] Figura 8. Módulos integrados en Cutpro [8]](https://img.interempresas.net/fotos/1459710.jpeg)
Por otro lado, existen modelos dinámicos que surgen con el objetivo de dar solución a la problemática de chatter. En este sentido destacan en el mercado aplicaciones comerciales basadas en el análisis acústico como Accord Mill. El software analiza la señal acústica grabada durante el proceso de mecanizado, para detectar las frecuencias de chatter y determinar las condiciones optimas de mecanizado a partir de este criterio. En esta línea acústica trabaja también Harmonizer, que a partir de la señal acústica proporciona la velocidad de giro estable en función de la profundidad de corte.
Este tipo de modelos requiere de equipamiento necesario para la adquisición de datos y el análisis de frecuencia. Con este objetivo, se desarrolla SMARTbox, que permite analizar las diferentes frecuencias de corte y armónicos del husillo de la máquina y así poder establecer un criterio predictivo contra condiciones desfavorables de mecanizado.
Otro ejemplo comercial de aplicación de modelos dinámicos es Machining Navi, que presenta un control de chatter online integrado en el control de la máquina y que permite variar las condiciones de mecanizado para evitar condiciones de corte inestables.
- Modelos basados en el Método de Elementos Finitos
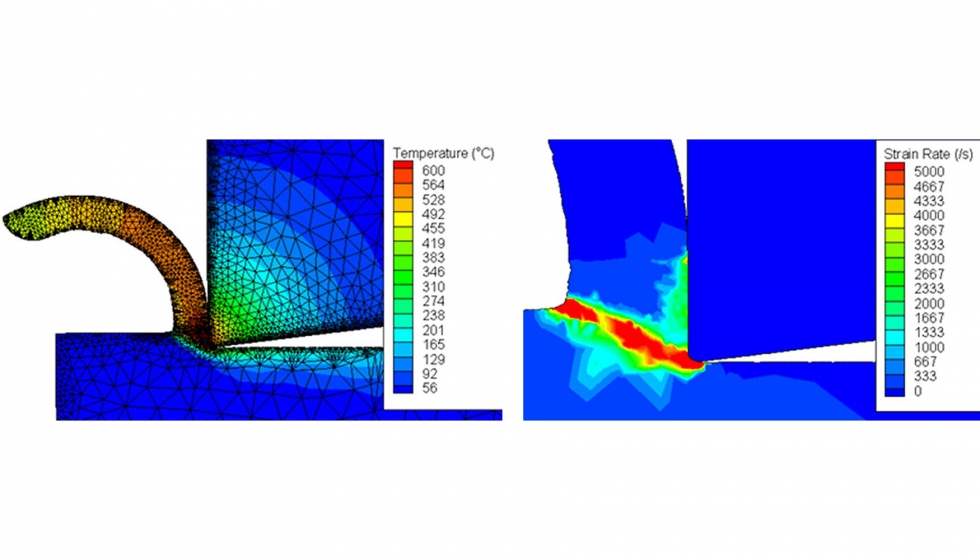
En las últimas décadas, la simulación mediante el Método de Elementos Finitos (MEF) ha tenido un gran auge y son muchos los trabajos que utilizan estos modelos para simular el proceso de corte y predecir la formación de viruta, fuerzas de corte, tensiones, deformaciones, tasas de deformación y temperaturas que se dan en el corte. Es especialmente importante que el análisis mediante el Método de Elementos Finitos puede ayudar a investigar algunos efectos termodinámicos que ocurren en la zona de corte que, de otra manera, no podrían ser medidos directamente. Un ejemplo de dichos efectos es la influencia de los recubrimientos de las herramientas de corte en la transferencia de calor y fricción, y la distribución de la temperatura resultante en la viruta y herramienta.
Para realizar un modelo realista del proceso de corte mediante este método es necesario realizar la formulación del modelo, aplicar la estrategia a emplear en la generación de mallado, determinar las condiciones de contorno y modelizar el material de la pieza y herramienta. La selección más apropiada de estas características a menudo determina la calidad del análisis que se lleva a cabo. En función de la elección de los ‘correctos’ parámetros algunas características se ven influenciadas y determinadas, tales como, las fuerzas de corte, temperaturas y la morfología de la viruta obtenida en la simulación. Por ejemplo, los modelos del material de la pieza y de fricción en la interface herramienta-viruta que se emplean se consideran de gran importancia en los resultados obtenidos en el análisis. Actualmente podemos decir que aún no existen esos parámetros ‘correctos’ ya que se sigue investigando en los parámetros que den los mejores resultados consiguiendo la mínima discrepancia entre las simulaciones y los resultados experimentales [9].
De la misma manera que ocurre con los modelos mecanísticos, la mayoría de estos desarrollos no llegan a transferirse a la producción por las dificultades antes mencionadas. Sin embargo, cabe destacar que actualmente existen algunos paquetes de elementos finitos comerciales de mecanizado de fácil uso, como el AdvantEdge y Deform. Estos paquetes, están orientados al mecanizado para simular tanto en 2D como en 3D operaciones tales como torneado, fresado y taladrado entre otros.
Por ejemplo, el AdvantEdge utiliza un código Lagrangiano, explícito y dinámico que realiza un análisis termo-mecánico acoplado. Aplica un mallado adaptativo automático y remalla de forma continua. El inconveniente de este software es que algunos parámetros son fijos y el usuario no puede intervenir. Así, por ejemplo, el coeficiente de fricción es constante en la intercara herramienta-viruta no siendo muy adecuado para proporcionar buenas aproximaciones de las fuerzas. Por otro lado, Deform utiliza códigos implícitos y para la separación de la viruta se aplica un criterio de daño y eliminación de elementos. Otras diferencias se refieren al modelo de fricción, los tipos de elementos y el modelo de material.
Comparando los resultados obtenidos de estos modelos de elementos finitos con los resultados experimentales, se ve que hay algunas discrepancias en ciertos parámetros. Estas diferencias son debidas principalmente a que los datos que emplean para modelizar el comportamiento del material deben ser mejorados ya que normalmente no se obtienen para tasas de deformación tan elevadas como las encontradas en el mecanizado. La modelización de la fricción también necesita ser ajustada para proporcionar resultados más adecuados, ya que aunque las fuerzas de corte se ajustan bastante bien a las obtenidas experimentalmente las fuerzas de empuje están normalmente subestimadas.
Por tanto, podemos concluir que aunque cuantitativamente estos modelos no den unos resultados del todo exactos con los obtenidos experimentalmente, cualitativamente resultan ser una herramienta muy útil ya que permiten predecir la forma de la viruta, fuerzas de corte, temperaturas de la pieza y herramienta, desgaste de herramienta y tensiones residuales ensayando diferentes condiciones de corte de partida y así reducir en gran medida los costosos ensayos de prueba y error.
Un ejemplo claro de aplicación es el caso de los fabricantes de herramienta, que utilizan programas como el AdvantEdge en el desarrollo de sus prototipos. Estos programas les permiten realizar las primeras tareas de optimización de sus diseños de herramientas minimizando iteraciones con ensayos de prueba y error. Así, pueden identificar a priori el diseño más eficiente, optimizar los rompevirutas u obtener un mayor conocimiento de los mejores grados de herramienta, recubrimientos, geometrías y condiciones de corte.
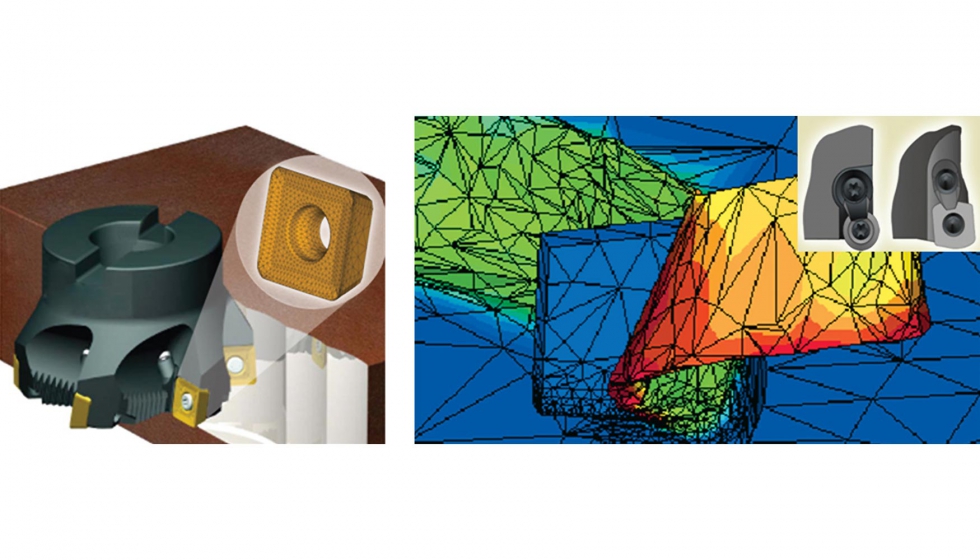
Figura 10. Izq.: Geometria de herramienta de Kennametal para simular mediante AdvantEdge FEM 3D. Dcha: Análisis de diferentes geometrías de insertos realizada por Hitachi Tool Engineering mediante AdvantEdge FEM 3D. [10].
Referencias
[1] Grzesik, ‘Advanced Machining Processes of Metallic Materials (Second Edition), Theory, Modelling, and Applications’, ISBN: 978-0-444-63711-6, Elsevier, 2016
[2] www.intes.de
[3] http://www.malinc.com
[4] K. Liu, M. Sun, T. Zhu, Y. Wu, Yu Liu, ‘Modeling and compensation for spindle's radial thermal drift error on a vertical machining center’, International Journal of Machine Tools and Manufacture, 105 (2016) 58–67.
[5] T. Schmitz, B. Mann, ‘Closed Form Solutions for Surface Location Error in Milling’, International Journal of Machine Tools and Manufacture, 46 (2006) 1369-1377.
[6] A. Lamikiz, L.N. López de Lacalle, J.A. Sánchez, U. Bravo. Calculation of the specific cutting coefficients and geometrical aspects in sculptured surface machining. Machining Science and Technology, 9 (3), 411-436.
[7] M. Arizmendi, J. Fernández, L.N. López de Lacalle, A. Lamikiz, A. Gil, J.A. Sánchez. Model development for the prediction of surface topography generated by ball-end mills taking into account the tool parallel axis offset. Experimental validation. CIRP Annals-Manufacturing Technology, 57 (1), 101-104.
[8] http://www.malinc.com/products/cutpro/
[9] Markopoulos, ‘Finite Element Method in Machining Processes’, ISBN 978-1-4471-4329-1, Springer, 2013.
[10] http://www.thirdwavesys.com/success-stories/








