La modelización como elemento de mejora de los procesos de arranque de viruta
Los fenómenos a reproducir son los relativos a la deformación del material en el proceso, a la fricción en las zonas de contacto con la herramienta y a la distribución del calor generado entre la herramienta, viruta y pieza.
La modelización de los procesos permite calcular y evaluar las mejores condiciones de mecanizado, sin realizar costosas pruebas de ensayo y error. Es por tanto una útil herramienta para llegar a optimizar los procesos obteniendo su máximo rendimiento y para mejorar el diseño de las herramientas de corte.
A fecha de hoy existen dos grandes grupos de modelos, que buscan estudiar distintos problemas y poseen diferente motivación:
- Numéricos basados en la técnica de los elementos finitos (FEM, Finite Elements Method): son simulaciones largas y costosas computacionalmente, de un solo virutazo. Buscan obtener las fuerzas de mecanizado, y especialmente los mapas térmicos en la herramienta de corte. Están encaminados a mejorar el diseño de las herramientas y obtener mucha información del propio proceso de arranque de viruta. Son la llave para el óptimo diseño de las herramientas de corte.
- Empíricos o mecanísticos, que caracterizan el binomio material/herramienta por unos coeficientes específicos de corte, que luego se introducen en unas expresiones matemáticas que los relacionan con la sección de viruta y la longitud del filo de corte. Se ejecutan en muy pocos segundos. Solo obtienen las fuerzas de corte durante el mecanizado, no las temperaturas. Son de utilidad para el cálculo de la potencia consumida, para el dimensionamiento de cabezales y máquinas y para la definición de formas de mecanizado que disminuyan errores dimensionales.
Por supuesto además de los anteriores siguen vigentes los modelos básicos y clásicos del corte, de tipo analítico.
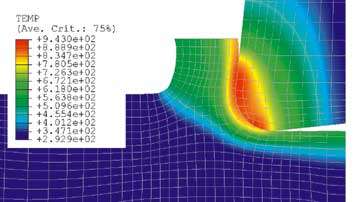
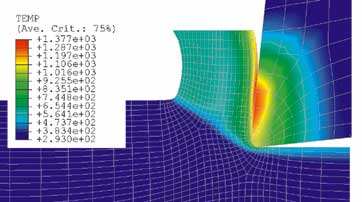
Simulación numérica del proceso de formación de la viruta
Al contrario que los modelos analíticos, permite tener en cuenta los efectos no lineales del contacto en la intercara de la viruta y herramienta, así como el comportamiento del material en fluencia.
Aparte de un modelo numérico en el que se deberán especificar la topología de la malla, dimensiones del modelo, condiciones de contorno, se necesitarán además al menos un total de hasta una veintena de parámetros de entrada relativos al material y contacto que deben ser adecuadamente identificados: ley de comportamiento en fluencia, rozamiento entre viruta y herramienta, resistencia térmica de contacto...
Es importante señalar que, de manera generalizada el comportamiento del material y el contacto son analizados desde un punto de vista macroscópico, siendo el material considerado como homogéneo e isotrópico, lo que supone una limitación.
La figura 1 muestra dos ejemplos realizados por Margune del campo de temperaturas obtenido con el modelo numérico en 2D, cuando se hace pasar el valor del espesor de viruta (avance) de 0,05 a 0,3 mm. La velocidad de corte es de 300 m/min, el ángulo de desprendimiento es de +6º y el radio de acabado de la arista de corte tiene un valor de 50 mm, siendo el material pieza un 42CrMoS4 y el material herramienta carburo metálico calidad P10.
Como se puede observar en las figuras el incremento del avance de 0,05 mm a 0,30 mm (aumento de 6 veces) produce un aumento de del valor máximo de la temperatura en 388 K (51 %). Asimismo se produce un aumento de la fuerza de corte en 445 N (332 %) y de la fuerza de avance en 68 N (78 %).
Dichos resultados muestran una coincidencia a nivel cualitativo con los resultados experimentales: Trent (1977) observó que el aumento del avance de 0,125 mm/v a 0,5 mm/v (en cuatro veces) provoca el aumento en la temperatura en 190 K, es decir un 25%. Conclusiones similares pueden ser extraídas sobre la validación de otras variables como las fuerzas de corte y de avance.
En definitiva, que del trabajo realizado hasta la actualidad se concluye que aunque es importante que el modelo numérico necesario sea correcto el rigor de los datos correspondientes a los parámetros de entrada, principalmente relativos al material y contacto, son fundamentales. Mientras tanto, la modelización numérica del proceso de corte deberá ser considerada como una herramienta robusta que aporte datos a nivel cualitativo, que permite en consecuencia la reducción del coste experimental.
Por otro lado y de cara a aportar un mayor valor industrial en el futuro, será necesario realizar una integración multiescala (micro-meso-macro) y mutifísica, tal y como lo señalan diversas prospectivas (www.imti21.org).

Simulación mecanística
Dentro de Margune se ha realizado un modelo de fuerzas de corte aplicable a fresa de geometría compleja. Con él se llega a obtener la fuerza de corte en el proceso de fresado, tal como se puede ver en la figura 2.
El valor de las fuerzas de corte es clave para definir las formas de trabajo que minimicen los errores debidos a la flexión de las herramientas. Por este motivo el modelo desarrollado se ha integrado en un CAM con objeto de llegar a definir trayectorias de mecanizado que impliquen una precisión y rugosidad final adecuadas, dentro de las tolerancias de la aplicación.
Las tres líneas de desarrollo son:
- Disminuir los errores debido a la flexión de las herramientas, interesante para fresado de moldes, matrices y microfresado.
- Reducir la deformación en el mecanizado de paredes delgadas, presentes en los componentes aeronáuticos.
- Establecer la estabilidad del fresado de componentes de rigidez reducida, de interés para fuselajes y satélites.



