Info

Verne - Un centro de mecanizado de cinemática paralela de 5 ejes

Myriam Terrier (a), Marta Giménez (b), Jean-Yves Hascoët (a) (a) Institut de Recherche en Communications et Cybernétiques de Nantes (IRCCyN), 1 rue de la Noë, BP 92101, 44321 Nantes Cedex03, France - (b) FATRONIK, Pol.Ind. Ibaitarte, 1, P.O.Box 160, 20870 Elgoibar (Gipuzkoa)-Spain15/11/2004
4389
Hace diez años, se presentó en Chicago un nuevo modelo de máquinas herramienta, basado en arquitecturas de cinemática paralela. Desde entonces, se han desarrollado en todo el mundo muchas máquinas de cinemática paralela (PKMs). Su mayor interés recae en las características de alta dinámica que podrían ayudar a agilizar el mecanizado de alta velocidad. Con el fin de desarrollar el mecanizado de alta velocidad en máquinas herramienta de cinemática paralela, y de poner en relieve su potencial, el laboratorio francés IRCCyN se ha equipado con VERNE, un centro de mecanizado de cinemática paralela desarrollado por el Centro Tecnológico FATRONIK. Sin embargo, el proceso del mecanizado a alta velocidad es una tarea compleja, en la cual un gran número de parámetros influye en la precisión de la pieza final y en la productividad de la máquina. Así, los parámetros NC y CAM (feed forward, estrategias de mecanizado,...), la geometría de la pieza, la estructura de la máquina, la herramienta,.... tienen una influencia directa en la pieza final. Por lo tanto, se ha desarrollado un método que, mediante dos aproximaciones, permite determinar la capacidad de la máquina (tanto serie como paralela) para mecanizar. La primera es la aproximación experimental (mediante el uso de una máquina de medición por coordenadas, o mediante la adquisición de la lectura de los encoders de los ejes); la segunda es una aproximación simulada. Inicialmente se presentará la cinemática de VERNE y, a continuación, se analizarán los resultados de los ensayos experimentales realizados hasta la fecha.
Desde la presentación de la primera máquina herramienta de cinemática paralela (PKM) en 1994 en Chicago, se carece de información específica de estas máquinas en mecanizado. Además, su “aparente complejidad” no ayuda a su implantación en la industria. Por lo tanto, se considera importante y urgente estudiar el comportamiento real de estas máquinas en mecanizado. En un estudio previo [1] se ha demostrado que las PKMs tienen potencial para el mecanizado de superficies libres de forma y, por lo tanto, para el mecanizado de alta velocidad. De hecho, algunas de las PKMs estudiadas demostraron alcanzar el mismo nivel de calidad que las máquinas herramientas de cinemática serie (SKMs). Sin embargo, deberán realizarse más experimentos para probar su comportamiento en todo tipo de operaciones de mecanizado (superficies libres de forma, taladrado, de 2 a 5 ejes,...).

Esta es la razón por la cual el IRCCyN [2] ha adquirido una máquina de cinemática paralela desarrollada por Fatronik [3]. El objetivo de este artículo es, en primer lugar, presentar la nueva máquina de Fatronik y, en segundo lugar, mostrar los primeros resultados en mecanizado, especialmente en el mecanizado de superficies libres de forma.

Verne una nueva máquina híbrida de mecanizado en 5 ejes

El mecanismo de Verne

Verne es un centro de mecanizado de cinemática paralela de 5 ejes que ha sido desarrollado por el Centro Tecnológico Fatronik. Su característica principal es que combina cinemática paralela y serie, perteneciendo así a la familia de máquinas híbridas. El módulo paralelo proporciona las traslaciones X, Y y Z; el módulo serie es una mesa basculante (tilting) que proporciona los ángulos B y C tal y como se muestra en la Figura 1. El eje del cabezal está inclinado 30º respecto de la vertical y, el volumen de trabajo está libre de singularidades.

Figura 1: Vista esquemática de VERNE
Figura 1: Vista esquemática de VERNE
El modulo paralelo se compone de seis brazos de longitud fija, siendo dos de ellos más cortos (brazo 1 [B1A1] y brazo 4 [B4A4] de la Figura 2). Los brazos unen la plataforma móvil con la estructura a través de tres guías lineales.
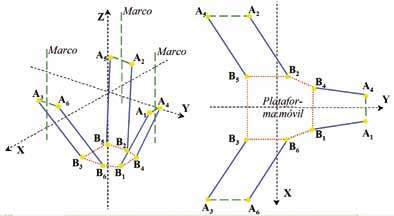
Figura 2: Módulo paralelo de VERNE
Figura 2: Módulo paralelo de VERNE
La cinemática de Verne

En esta sección, se explican las transformadas cinemáticas. Las coordenadas cartesianas (pieza) se denominan como [X, Y, Z, B, C] y las de la máquina como {V1, V2, V3, Ba, Ca}.

Con el fin de definir el movimiento de la máquina, se han utilizado tres conjuntos de sistemas de coordenadas, tal y como se muestra en la Figura 3. El primero es el sistema de coordenadas absoluto R0 , que está ligado a la estructura de la máquina. El segundo es el sistema de coordenadas de programación RM de 5 ejes, vinculado a la mesa basculante (tilting). El último es el sistema de coordenadas del cabezal RT.

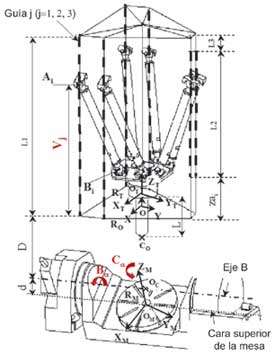
* D, d, L1, L2, L3, y zai son parámetros de diseño y L es la longitud de la herramienta. Figure 3: Geometría de VERNE
* D, d, L1, L2, L3, y zai son parámetros de diseño y L es la longitud de la herramienta. Figure 3: Geometría de VERNE
La transformada cinemática se consigue mediante un conjunto de seis ecuaciones, que representan la distancia en coordenadas cartesianas entre las articulaciones Bi de la plataforma y las articulaciones Ai del carro:
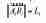
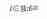
Imagen
donde Li es la longitud del brazo i
Imagen
Nota:
Imagen
(número de brazos) y
Imagen
número de guías)

Las seis ecuaciones son:

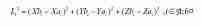
Imagen
En las cuales:
Imagen
Nota: L es la longitud de la herramienta.

En estas ecuaciones, los vectores {xbi, ybi, zbi} y {xai, yai, zai} son parámetros de diseño conocidos.

Cuando el problema considerado es la transformada inversa, los valores conocidos son {X, Y, Z, B, C} y las incógnitas son {V1, V2, V3, Ba, Ca}. Sin embargo, en lo que a la transformada directa se refiere, los valores conocidos son {V1, V2, V3, Ba, Ca} y las incógnitas son {X, Y, Z, B, C}. Como el sistema es no lineal y, está compuesto por seis ecuaciones para solamente cinco incógnitas [X, Y, Z, B, C], se utiliza un método numérico (algoritmo de Newton-Raphson) para resolverlo. Por consiguiente, con esta transformada se puede controlar Verne.

Estos modelos cinemáticos (principalmente la transformada directa) son de gran importancia para la transformación de los datos de los encoders en coordenadas cartesianas, tal y como se explica en el apartado 3.3.

Los primeros resultados de mecanizado en Verne

Geometría de la pieza test

Las primeras pruebas se han realizado con la pieza test de la Figura 4, que contiene las principales superficies libres de forma que pueden encontrarse en la industria del molde y matriz [1]

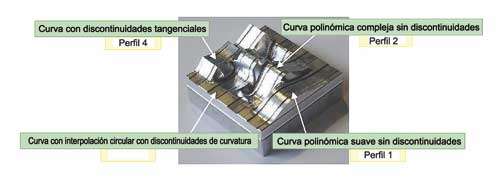
Figure 4: Geometría de la pieza test P1100
Figure 4: Geometría de la pieza test P1100
Máquina de Medir por Coordenadas

Las piezas se han mecanizado en bloques de aleación de aluminio. En un primer paso las mediciones se han realizado en una Máquina de Medir por Coordenadas (CMM), ya que la pieza test está compuesta por superficies libres de forma (Figura 5).

Figura 5: Máquina de Medición por Coordenadas
Figura 5: Máquina de Medición por Coordenadas
Se han realizado varias pruebas con el fin de analizar la influencia de la calibración, de la posición de la pieza en el área de trabajo, del método de interpolación de la trayectoria de la herramienta y, finalmente, de la velocidad de avance programada. Es importante mencionar que los resultados aquí presentados reflejan las potencialidades de Verne en el momento en que se han llevado a cabo las pruebas.

En un segundo paso, tal y como se explica en el apartado 3.3, se han realizado mediciones a partir de la lectura de los encoders.

Imagen
La calibración consiste en ajustar los parámetros cinemáticos del módulo paralelo. En VERNE existen un total de 42 parámetros cinemáticos que definen la cinemática de su módulo paralelo ([“12 articulaciones” x “3 coordenadas cartesianas x, y, z”] + “6 longitudes de brazos”). Para calibrar Verne, Fatronik utiliza un doble BallBar [4] y una pieza con tres esferas que forman un triedro, como se muestra en la figura 6 [5]. Para cada esfera, se realizan interpolaciones circulares paso a paso. Para cada una de la posiciones, se mide la longitud del BallBar y se introduce el dato en un algoritmo de optimización que determina los valores de los 42 parámetros cinemáticos.

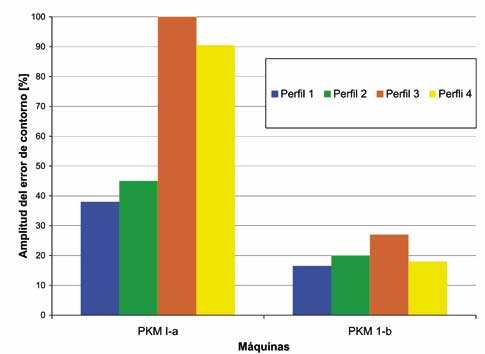
Con el fin de analizar la influencia de la calibración, se mecanizó una pieza antes de la primera calibración de la máquina (PKM I-a) y, otra justo después (PKM I-b). En la Figura 6 se representa la amplitud del error de contorno (expresado en porcentaje) para los cuatro perfiles y las dos configuraciones de máquina (antes y después de calibrar). El error de contorno es el error de componente, ortogonal a la trayectoria deseada (es decir, la desviación mínima de la trayectoria real respecto de la deseada, según la normal).

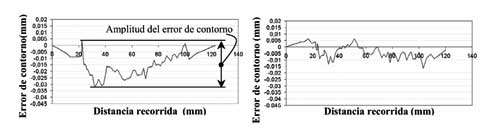
Nota: La amplitud del error de contorno se define como la diferencia entre el error de contorno máximo y el mínimo, medidos en la CMM (Figura 9).

La primera calibración permite reducir aproximadamente tres veces la amplitud del error de contorno. Por lo tanto, queda de manifiesto la gran importancia de la calibración para la precisión de la máquina. Verne volverá a ser calibrada de nuevo en unos meses, por lo que, probablemente, mejorará de nuevo su precisión.

Todos los resultados que se exponen en los siguientes párrafos corresponden a la configuración tras la calibración, PKM I-b.

Figura 6: Influencia de la calibración
Figura 6: Influencia de la calibración
Influencia de la orientación de la pieza

Las piezas PKM I-a y PKM I-b (también denominada en esta sección PKMI-b_0) se han colocado paralelamente al eje X (q=0°, ver Figura 8). Con el fin de determinar la influencia de la orientación de la pieza en la mesa, se han mecanizado dos piezas más; así, PKM I-b_90 corresponde a una colocación paralela al eje Y (q=90°), y PKM I-b_45 a un posicionamiento a 45° (q=45°).

Figura 7: Orientación de la pieza en la mesa
Figura 7: Orientación de la pieza en la mesa
La Figura 9 muestra la amplitud del error de contorno, medido en la CMM, para cada perfil y cada orientación.

Se demuestra que la orientación de la pieza paralela al eje Y (PKM I-b_90) proporciona la mejor precisión, cualquiera que sea el perfil considerado. Este resultado puede explicarse por la cinemática de la propia máquina. En realidad, debido al diseño del modulo paralelo, existe un grado de libertad extra (además de las tres translaciones X, Y, Z)

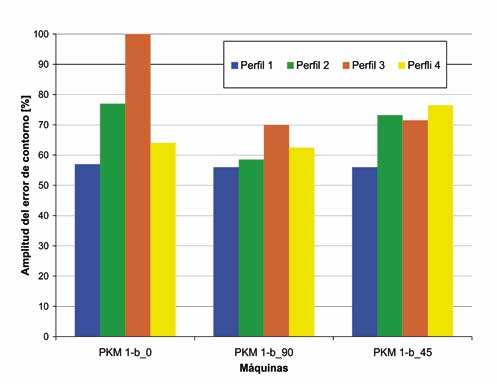
Figura 8: Influencia de la orientación de la pieza en la mesa
Figura 8: Influencia de la orientación de la pieza en la mesa
ue es el movimiento rotativo alrededor del eje Y. Por lo tanto, la mesa basculante debe compensar este grado de libertad extra. En consecuencia, para una trayectoria paralela al eje X se mueven el modulo paralelo y la mesa basculante (eje B), mientras que para una trayectoria paralela al eje Y se mueve sólo el módulo paralelo. Esta es la razón por la que la orientación paralela al eje Y se realiza con una precisión mayor, ya que sólo mueve el módulo paralelo.

Sin embargo, para la velocidad de avance programada (6m/min) la diferencia entre las tres orientaciones es limitada. Se están realizando más ensayos con el fin de estudiar la influencia de la velocidad de avance en la orientación de la pieza sobre la mesa.

Todos los resultados que se dan en los siguientes párrafos corresponden a la configuración de orientación paralela al eje Y (q=90°).

Influencia del método de interpolación de la trayectoria de herramienta

Con el fin de analizar este parámetro CAM, se ha mecanizado una pieza (colocada paralela al eje Y) usando un método de interpolación B-Spline (PKM I-c).

La Figura 9 indica el error de contorno medido en la CMM para el perfil 1. La escala es la misma para los dos gráficos. Considerando el perfil 1, se tarda 2.24s en realizar una pasada con un método de interpolación lineal (G1) y, 2.2s con una interpolación tipo B-Spline. Por consiguiente, para la velocidad de avance programada de 6m/min, la interpolación con B-Spline permite reducir el tiempo de mecanizado, a la vez que mejora la precisión.

Figura 9: Error de contorno para una interpolación tipo G1 (izquierda) y B-Spline (derecha)
Figura 9: Error de contorno para una interpolación tipo G1 (izquierda) y B-Spline (derecha).
La Figura 10 muestra que la interpolación con B-spline reduce la amplitud del error del contorno en todos los perfiles.
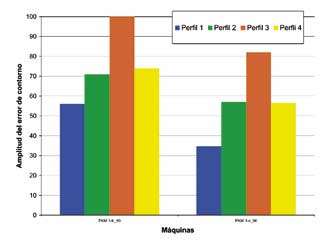
Figura 10: Influencia del método de interpolación de la trayectoria de herramienta
Figura 10: Influencia del método de interpolación de la trayectoria de herramienta
Influencia de la velocidad de avance programada

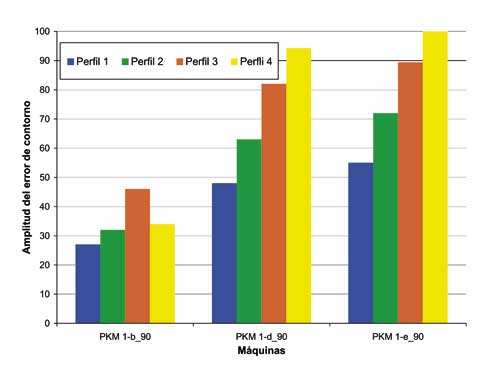
Los ensayos realizados hasta ahora se han llevado a cabo a una velocidad de avance programada de 6m/min, con una velocidad de cabezal de 18.000rpm (de PKM I-a a PKM I-c). Con el fin de estudiar el comportamiento de la máquina a diferentes velocidades de avance, en un primer paso se estableció una velocidad de avance de 7,7 m/min a 24.000 rpm (PKM I-d_90). En un segundo paso, la velocidad de avance programada se incrementó a 14.4m/min para una velocidad del cabezal de 24.000 rpm (PKM I-e_90). Como se ha mencionado anteriormente, la pieza se colocó paralela al eje Y (q=90°). En la Figura 11 se representa la amplitud del error de contorno medido en la CMM.

Es importante recordar que la máquina no se encuentra en su estado óptimo aún y que, por lo tanto, no se han optimizado todavía todos los parámetros de control. Este hecho puede explicar el distinto comportamiento a diferentes velocidades de avance programadas. Tan pronto como la máquina esté optimizada, se realizarán más pruebas y los datos obtenidos se compararán con los actuales. De cualquier forma, este análisis es de gran relevancia para mostrar la influencia de la velocidad de avance en la precisión, cuando la máquina no está bien ajustada.

Figura 11: La influencia de la velocidad de avance programada
Figura 11: La influencia de la velocidad de avance programada
Conclusiones de los ensayos

Estas primeras pruebas han demostrado la importancia de tener en cuenta todos los parámetros que influyen en el proceso de producción, con el objetivo de mejorar la precisión de las máquinas-herramienta (tanto de arquitectura serie como paralela). Comparando los resultados obtenidos en Verne con los del conjunto de máquinas-herramienta analizadas por el IRCCyN [1], se demuestra que esta máquina alcanza el mismo nivel de precisión que algunas SKM.

Sin embargo, debido al gran número de parámetros de mecanizado, su optimización no es lo suficientemente sencilla y rápida a la hora de mecanizar una pieza. Por consiguiente, una solución para ganar tiempo es analizar la lectura de los encoders, tal y como se explica en el próximo apartado.

Medidas con los encoders

En investigaciones previas en el IRCCyN, se ha desarrollado una nueva técnica para caracterizar una fresadora (es decir, para determinar la capacidad de una máquina para realizar una pieza con una tolerancia dada) [6], [7]. El objetivo principal es obtener las posiciones reales de la herramienta para cada eje, mediante la adquisición de la lectura de los encoders de los ejes durante el mecanizado, como se muestra en la Figura 13.

Figura 12: Adquisición de la lectura de los encoders en una PKM
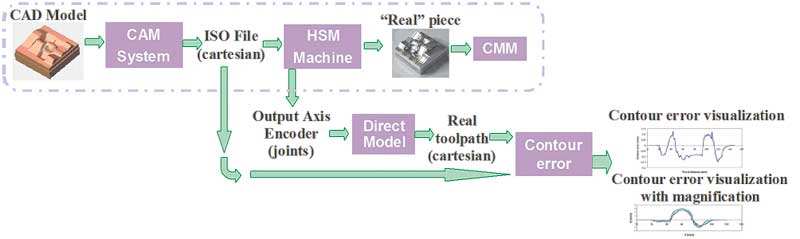
Imagen
Con el fin de transformar la información de los encoders, que corresponde a las posiciones de las articulaciones de la máquina (para Verne: {V1, V2, V3, Ba, Ca}), en las correspondientes coordenadas cartesianas, se utiliza la transformada directa presentada en el apartado 2.2. Así, se puede deducir la trayectoria real de la herramienta tal y como se realiza con las maquinas serie, comparándola con el programa ISO.

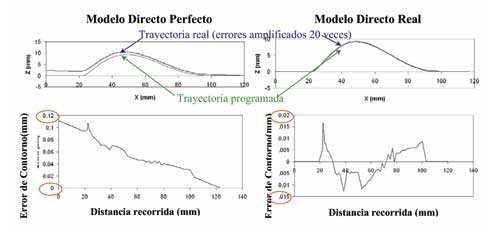
Nota: en lo que a la máquina Verne se refiere, el error máximo de transformada (directa o inversa) establecido en la pieza P1100 para los 4 perfiles (Figure 4) es de 3.5E-5mm. Así, estos errores son despreciables en la transformada directa, con la que se deduce la trayectoria real de la herramienta. (Figura 12).

Es importante tener en cuenta que para esta transformada se debe usar el modelo directo “real”. En realidad, en Verne se implementa un modelo en el Control Numérico para compensar los defectos de rectitud y paralelismo de los ejes. La Figure 13 muestra dos visualizaciones del error de contorno obtenidas a partir de los datos de los encoders.

Figure 13: Influencia del modelo directo
Figure 13: Influencia del modelo directo
El gráfico de la izquierda está generado a partir de un modelo directo perfecto, mientras que el de la derecha está generado a partir de un modelo directo real, que tiene en cuenta los defectos geométricos de la máquina. Resulta evidente que el modelo directo es de gran importancia en la interpretación de la lectura de los encoders. De hecho, el principal interés de la lectura de los encoders es que reproducen la trayectoria real de la herramienta. Por lo tanto, incluso si existe una pequeña diferencia entre los encoders y la realidad, (ya que la medida no ocurre a un mismo nivel, como se muestra en la Figura 13), la ventaja es que no necesitamos mecanizar una pieza para determinar el comportamiento de la máquina. Así, es posible optimizar, por ejemplo el CN, adquiriendo la información de los encoders, y luego mecanizar una pieza para confirmar que se consigue lo esperado. Este método está siendo aplicado actualmente en Verne.
Figura 14: Una superficie plana fresada en VERNE
Figura 14: Una superficie plana fresada en VERNE
Al mismo tiempo, se han llevado a cabo algunos tests de planeado de una superficie (Figura 15). Es realmente sencillo mecanizar este tipo de superficies en una máquina herramienta de arquitectura serie: siendo la trayectoria paralela a uno de los tres ejes, sólo el eje considerado es el que se mueve. Sin embargo, el planeado de una superficie en una máquina herramienta de cinemática paralela como Verne no es tan sencillo como en una máquina herramienta serie. De hecho, el control de la máquina será más complejo (casi todas las articulaciones se moverán para mecanizar esta superficie simple), y la trayectoria tendrá una gran influencia en la pieza final (como se dice en la sección 3.2.2, Verne tiene un grado de libertad extra que se compensa con la mesa basculante). Así, con el fin de estudiar este fenómeno, se ha recogido la lectura de los encoders para esta pieza test.

La visualización se ha realizado utilizando el interfaz de simulador de gráficos HSM [7] para obtener una visión realista de la pieza final. La Figura 15[a] corresponde a los datos de los encoders en el caso de Verne, mientras que la Figura 15[b] corresponde a los datos de los encoders en el caso de una máquina herramienta de arquitectura serie de 3 ejes.

Se constata la influencia de la arquitectura de la máquina en los resultados finales. Sin embargo, es importante recordar que la ventaja principal de las máquinas herramienta de cinemática paralela es su dinámica, que resulta más elevada que en las máquinas herramientas de arquitectura serie. Por lo tanto, se realizarán nuevas pruebas con el fin de determinar el campo de aplicación de las PKM.

Figura 15: Visualización de la información de los encoders en el caso de una superficie plana
Figura 15: Visualización de la información de los encoders en el caso de una superficie plana

Conclusión

Diez años después de la primera presentación de una PKM en Chicago, algunas de estas máquinas están mecanizando hoy en día piezas con una buena precisión. El objetivo de este artículo no es el de comparar Verne con otras máquinas, puesto que todavía no está optimizada. Si embargo, las primeras pruebas han permitido demostrar que la calibración es de gran importancia para la precisión final de la máquina. Además, dependiendo de la arquitectura paralela, la orientación de la pieza final puede también mejorar en gran medida su precisión. Con respecto a los parámetros CAM, como el método de interpolación de la trayectoria de la herramienta, se ha demostrado en un estudio previo [1] que la interpolación mediante B-Spline reduce el error de contorno en las PKM, igual que en las SKM. Las pruebas llevadas a cabo en Verne confirman esta tendencia. Finalmente, y debido a que la ventaja principal de las PKM reside en sus características dinámicas, se han realizado una serie de experimentos con diferentes velocidades de avance programadas. Es importante recordar una vez más, que los resultados proporcionados en este estudio no representan la capacidad real de Verne, ya que ésta no se encuentra todavía completamente optimizada. Se va a realizar una nueva calibración, que debería mejorar su rendimiento, y se llevarán a cabo más pruebas para demostrar el potencial de Verne en el mecanizado de todo tipo de superficies.

Por el momento, se concluye que Verne puede alcanzar el mismo nivel de productividad que algunas SKM.

Referencias

[1] TERRIER M., DUGAS A., HASCOËT J.Y., Qualification of parallel kinematics machines in high-speed milling on free form surfaces, International Journal of Machine Tools and Manufacture, Vol 44, pp 865-877, 2004

[2] Institut de Recherche en Communications et Cybernétiques de Nantes (IRCCyN), 1 rue de la Noë, BP 92101, 44321 Nantes Cedex03, France

[3] FATRONIK, Pol.Ind. Ibaitarte, 1, P.O.Box 160, 20870 Elgoibar (Gipuzkoa)-Spain, http://www.fatronik.com, Access July 2004

[4] RENISHAW, http://www.renishaw.com, Access July 2004

[5] MARTINEZ L., COLLADO V., Calibration of a Hybrid Serial/Parallel 5-Axes Milling Machine Using a Double BallBar Probe, 4th Chemnitz Parallel Kinematics Seminar, pp 137-150, Chemnitz, Germany, April 2004

[6] HASCOET J.Y., DUGAS A., LEE J.J., “Simulation des opérations d’usinage”, Rapport final du projet “Saut technologique UGV”, Institut de Recherche en Communications et Cybernétique de Nantes (IRCCyN), France, June, 2001, 161p

[7] DUGAS A., "CFAO et UGV - Simulation d’usinage de formes complexes", Thèse de Doctorat, Université de Nantes, Ecole Centrale de Nantes, France, 13 December, 2002

Empresas o entidades relacionadas

Fundación Fatronik, S.A. (Tecnalia)
Ver stand virtual
Renishaw Ibérica, S.A.U.
Ver stand virtual