Gestión integral del proceso de verificación volumétrica en máquina-herramienta mediante láser tracker
En este trabajo se presenta una herramienta versátil que permite realizar la verificación de cualquier tipo de máquina-herramienta mediante soluciones de nueva generación a través de la incorporación de nuevos procedimientos y modelos de verificación. Esta dota al sector de fabricantes de máquina-herramienta y empresas relacionadas con metrología industrial de las técnicas necesarias que permitan de una manera trazable identificar los errores cinemáticos y geométricos; teniendo en consideración las influencias que afectan a la precisión, tanto del sistema de medida como del propio sistema de fabricación. Lo que permite dar un salto cualitativo y cuantitativo en términos de reducción de tiempos de inspección, y con ello, un incremento en la productividad de los procesos de fabricación manteniendo, si no mejorando, la precisión y fiabilidad en los procesos asociados.
El software desarrollado permite realizar de manera íntegra todo el proceso de verificación tanto en máquinas con ejes lineales como giratorios, desde la generación del programa de control numérico con los puntos empleados en la verificación, hasta la generación de un nuevo programa de control numérico con la compensación de los errores geométricos de la máquina. Como no solamente es importante disponer de una herramienta que permita realizar la verificación aplicada a un determinado proceso de verificación, sino que resulta fundamental la flexibilidad del mismo, la aplicación se ha realizado teniendo siempre presente la generación de la ecuación de movimiento que define el modelo cinemático de la máquina a verificar, diferentes funciones de regresión a utilizar en función del tipo de eje de movimiento a caracterizar (lineal o giratorio), estrategias y secuencias de optimización así como los criterios de convergencia del proceso iterativo de identificación.
1. Introducción
La alta competitividad existente en un sector como el de la máquina-herramienta (MH), consecuencia de la gran cantidad de fabricantes y variedad disponible, presenta la precisión y la posibilidad de compensación de los errores como una diferencia competitiva entre máquinas y fabricantes.
Las distintas fuentes de error que afectan a la precisión de una máquina-herramienta se dividen en dos grandes grupos, errores cuasi-estáticos y errores dinámicos (figura 1).
Los errores cuasi-estáticos [1] son aquellos que afectan de manera relativamente lenta a la precisión de la máquina. Estos errores están formados por errores geométricos, errores cinemáticos, errores inducidos por las fuerzas de corte, etc. De estas fuentes de error, los errores geométricos son consecuencia de los elementos estructurales que conforman la máquina afectando a la repetibilidad y a la precisión cinemática de ésta [2]. Los errores cinemáticos son el resultado de la desalineación de los diferentes componentes estructurales que constituyen la máquina, determinando sus grados de libertad y secuencia de movimiento. Los errores térmicos son inducidos por las deformaciones termo-elásticas que sufren los diferentes componentes de la máquina como consecuencia de las fuentes de calor internas y externas de la misma [3, 4].
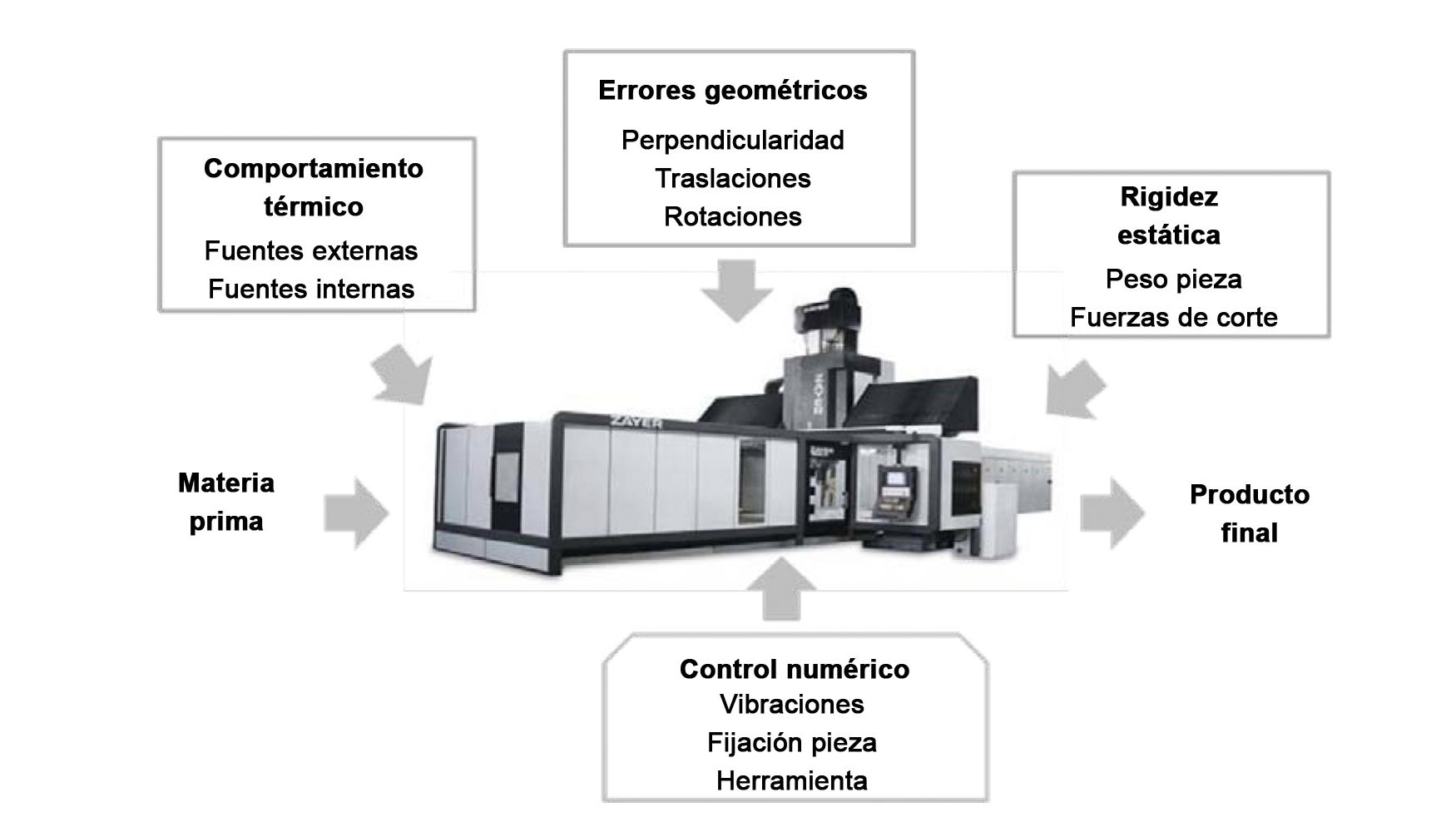
Sin embargo, los errores dinámicos [5] están causados por vibraciones de la máquina, error de movimiento de los husillos, errores del control, etc. Estos errores son particulares del funcionamiento de cada máquina y presentan fuertes variaciones en pequeños espacios de tiempo. En cómputo general, la influencia de los errores cuasi-estáticos en el error total de la máquina es mucho mayor que la influencia de los errores dinámicos, alcanzando valores en torno al 70%.
La mejora en la precisión de una máquina-herramienta se puede afrontar desde dos enfoques: evitar la aparición de errores y/o compensar el efecto de los errores ya existentes [6]. El correcto diseño y montaje de la máquina, junto con un ambiente controlado en condiciones de trabajo es considerado como la mejor manera de evitar la aparición de errores en la misma. Sin embargo, los costes de mecanizado aumentan exponencialmente a medida que aumenta la precisión requerida. La compensación presenta como ventaja fundamental una mayor libertad de diseño y una fuerte reducción de coste frente al diseño de precisión; siendo considerado al mismo tiempo como un método eficiente en la recuperación parcial de parte de la precisión inicial mediante la verificación periódica de la máquina.
La verificación mediante medición directa de los errores, también denominada verificación geométrica, ha sido tradicionalmente utilizada en verificación de máquina-herramienta y máquinas de medir por coordenadas. Esta técnica se basa en la caracterización de los errores de cada eje por separado, independientemente del modelo cinemático de la máquina y del movimiento del resto de los ejes. Los principales inconvenientes de esta técnica radican tanto en el tiempo necesario para la verificación, como en la corrección local de los errores. Este inconveniente es subsanado mediante la medición indirecta de los errores que permite, a partir de técnicas de verificación volumétrica, realizar una corrección de la influencia conjunta de los errores geométricos y cinemáticos de la máquina en todo su volumen de trabajo basándose en el movimiento multieje de la misma.
2. Principio de funcionamiento de la verificación volumétrica
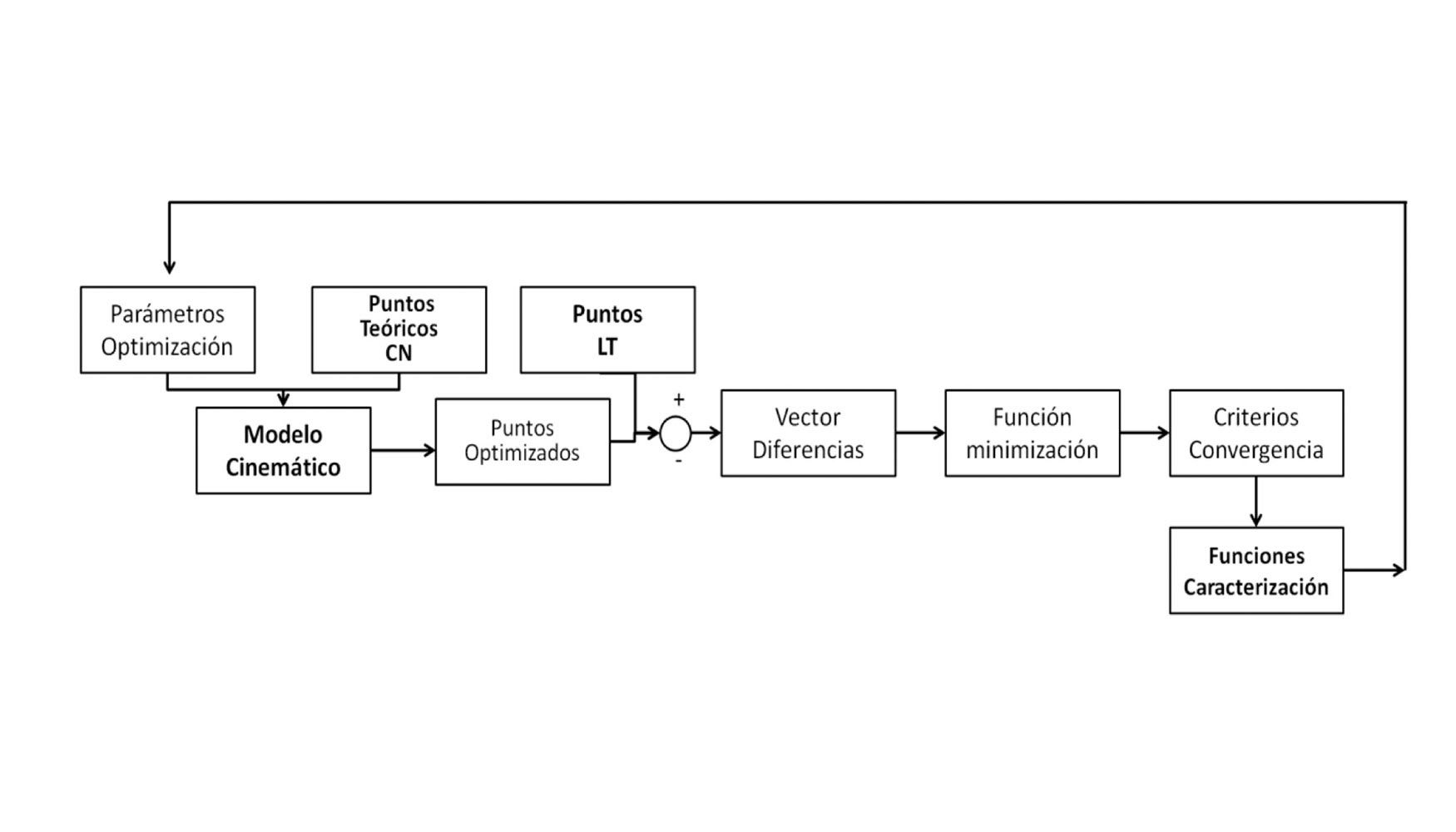
La verificación volumétrica se basa en la minimización de la diferencia entre puntos reales (medidos con laser tracker) y nominales (CN), que mostrará la influencia conjunta de todos los errores a partir del modelo cinemático de la máquina mediante el error volumétrico de la misma (ev) [7, 8].
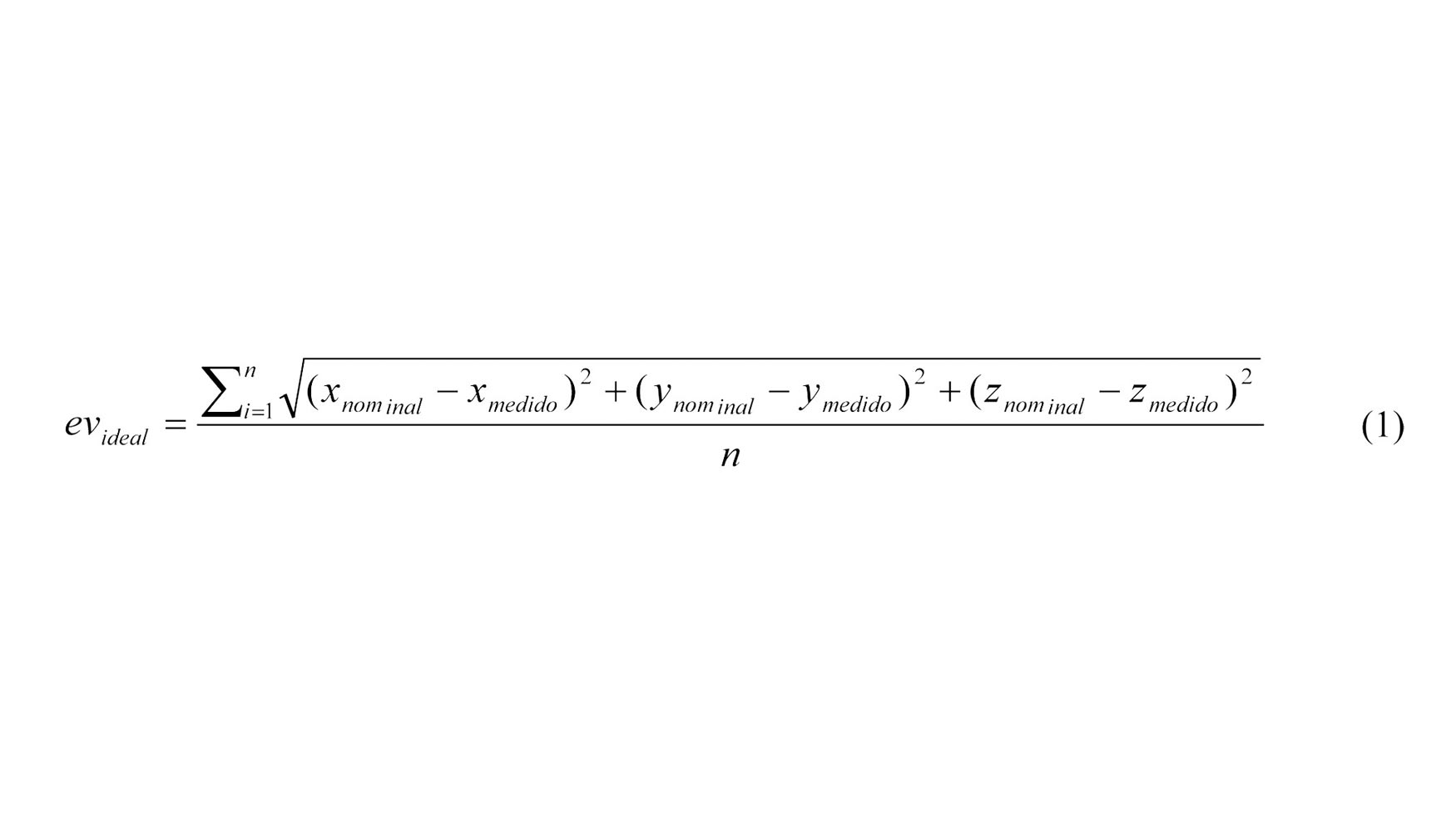
El error volumétrico ideal viene determinado por el error de posicionamiento de la máquina dentro de su volumen de trabajo consecuencia de los errores geométricos de la misma. Sin embargo, tanto la máquina-herramienta como el sistema de medida influyen en el error volumétrico obtenido mediante la medición de los puntos de verificación. El modelo cinemático de la máquina es inalterable ante la presencia de factores externos, sin embargo los componentes estructurales que definen la cadena cinemática a partir de los cuales se obtiene la ecuación de movimiento sí que modifican sus dimensiones como consecuencia de gradientes de temperatura. Del mismo modo, la incertidumbre de medida del sistema de medición utilizado afecta a la precisión de los puntos medidos. La diferencia de los puntos medidos con ruidos de medida se compara con los puntos nominales por lo que el error volumétrico obtenido está afectado a demás por este error.
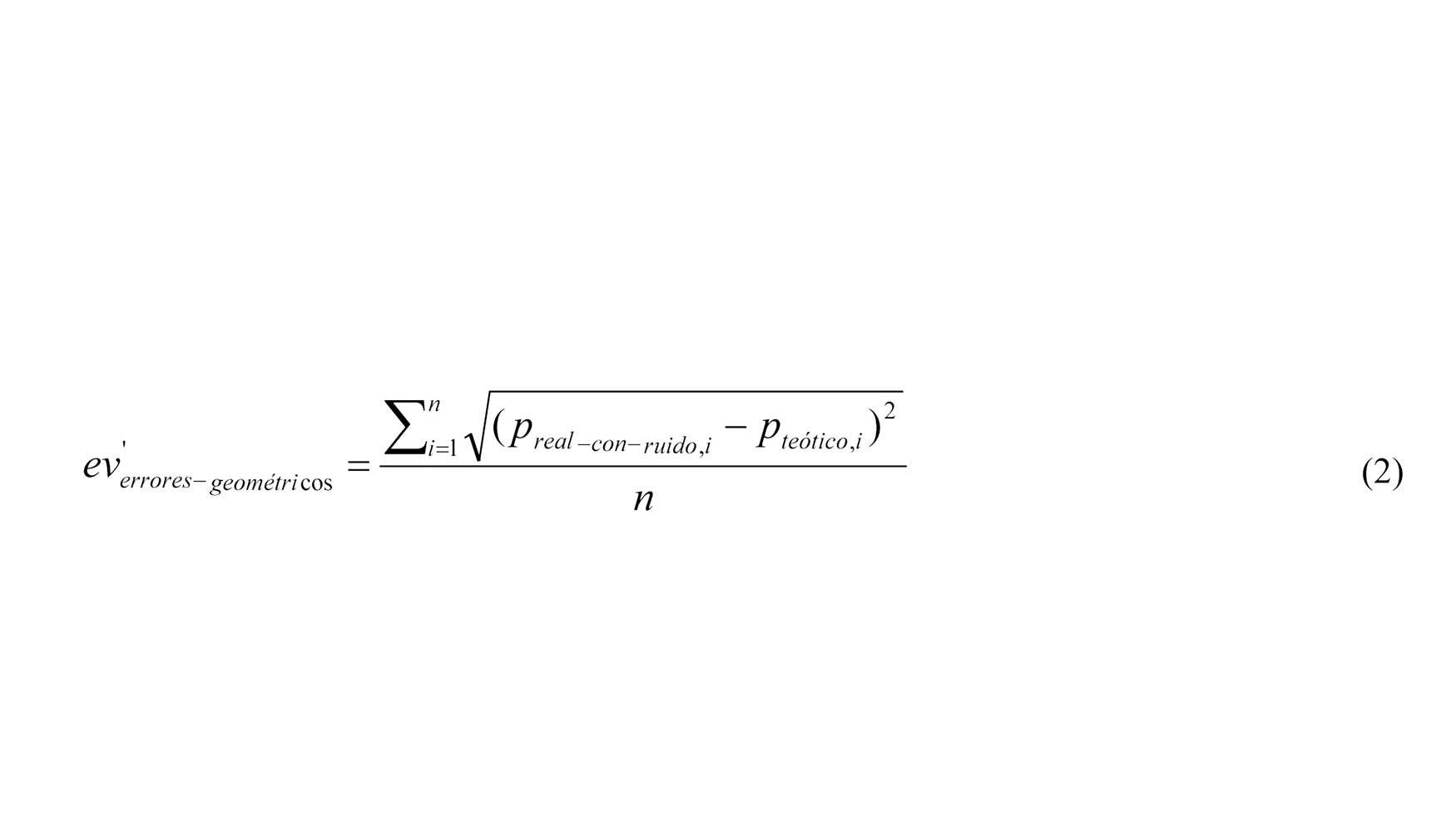
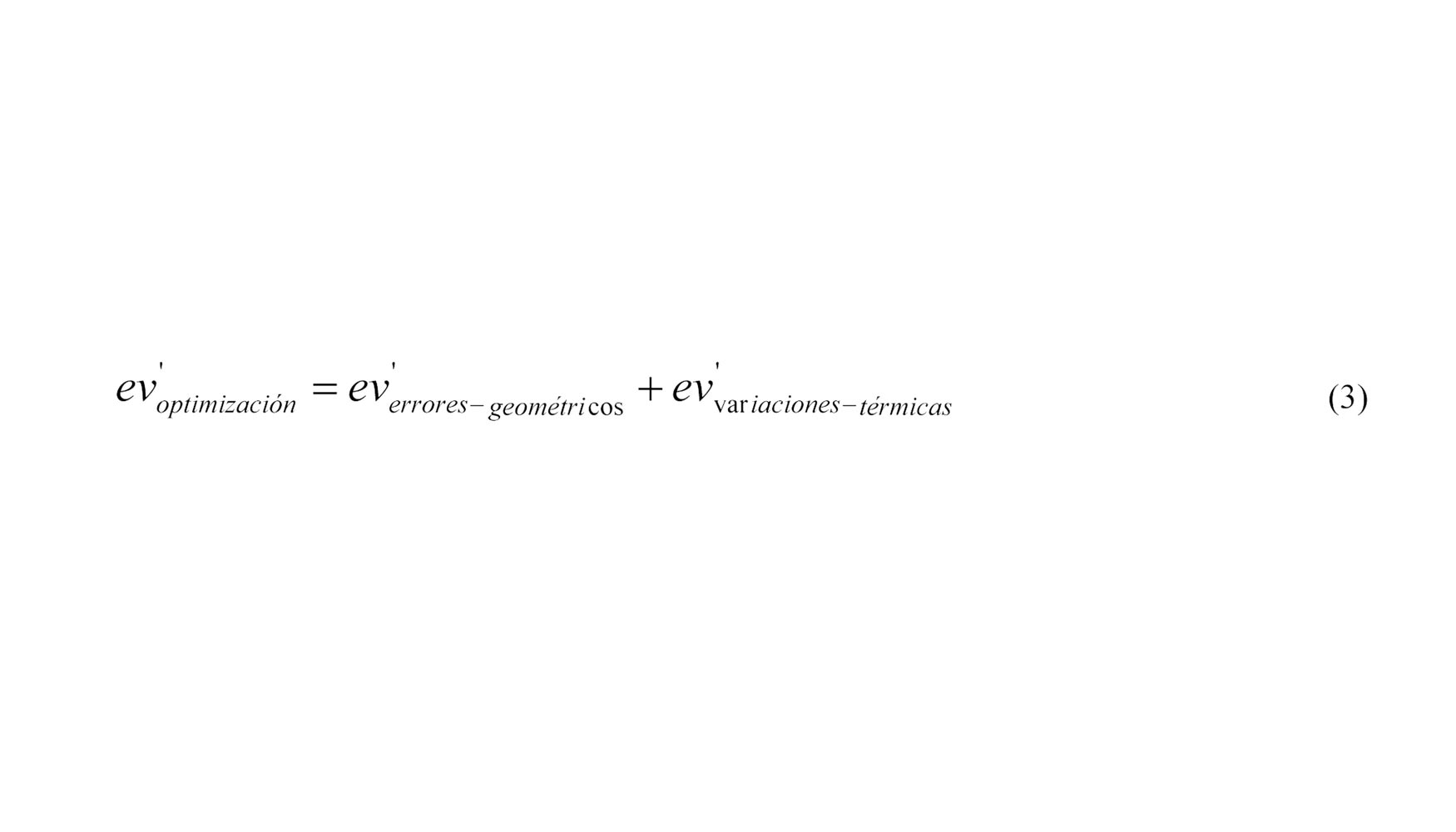
La aplicación de técnicas de multilateración y auto-calibración permiten conocer la posición de LT respecto a la máquina y reducir la influencia del ruido de medida angular este [9, 10]. Estas técnicas pretenden mejorar la precisión de los puntos capturados mediante la utilización de la información radial que proporciona la medición de un punto desde un mínimo de tres posiciones diferentes, a partir de las cuales determinar las coordenadas del punto medido sin información de la componente angular del LT.
A partir del error medido en dichos puntos y el modelo cinemático de la máquina afectados por todos los errores individuales de los ejes y por el sistema de medida empleado, es posible plantear un método iterativo de cálculo que permita minimizar el error de la máquina; obteniendo los valores de los errores individuales que hacen mínimo el efecto conjunto de todos ellos a partir del error volumétrico de la máquina. Para dotar de significado físico a las funciones de caracterización obtenidas es necesario introducir una serie de restricciones a la optimización; obteniéndose en cualquier caso una compensación precisa del error volumétrico [8].
3. Gestión integral del proceso de verificación volumétrica mediante láser tracker
A la hora de afrontar la verificación volumétrica en cualquier tipo de máquina es necesario definir cada una de las acciones que se deben llevar a cabo en función de las características y significado de las mismas:
- Adecuación y preparación de la máquina
- Medición y recopilación de información
- Tratamiento de datos y obtención de resultados
- Análisis de los resultados
- Acciones de mejora en la precisión de la máquina
El proceso de verificación define el orden en el que deben realizarse cada una de las acciones; siendo necesario para la realización de todas ellas una herramienta que permita una gestión integral del proceso de verificación de manera intuitiva.
3.1 Errores no geométricos con influencia en el error volumétrico de la máquina
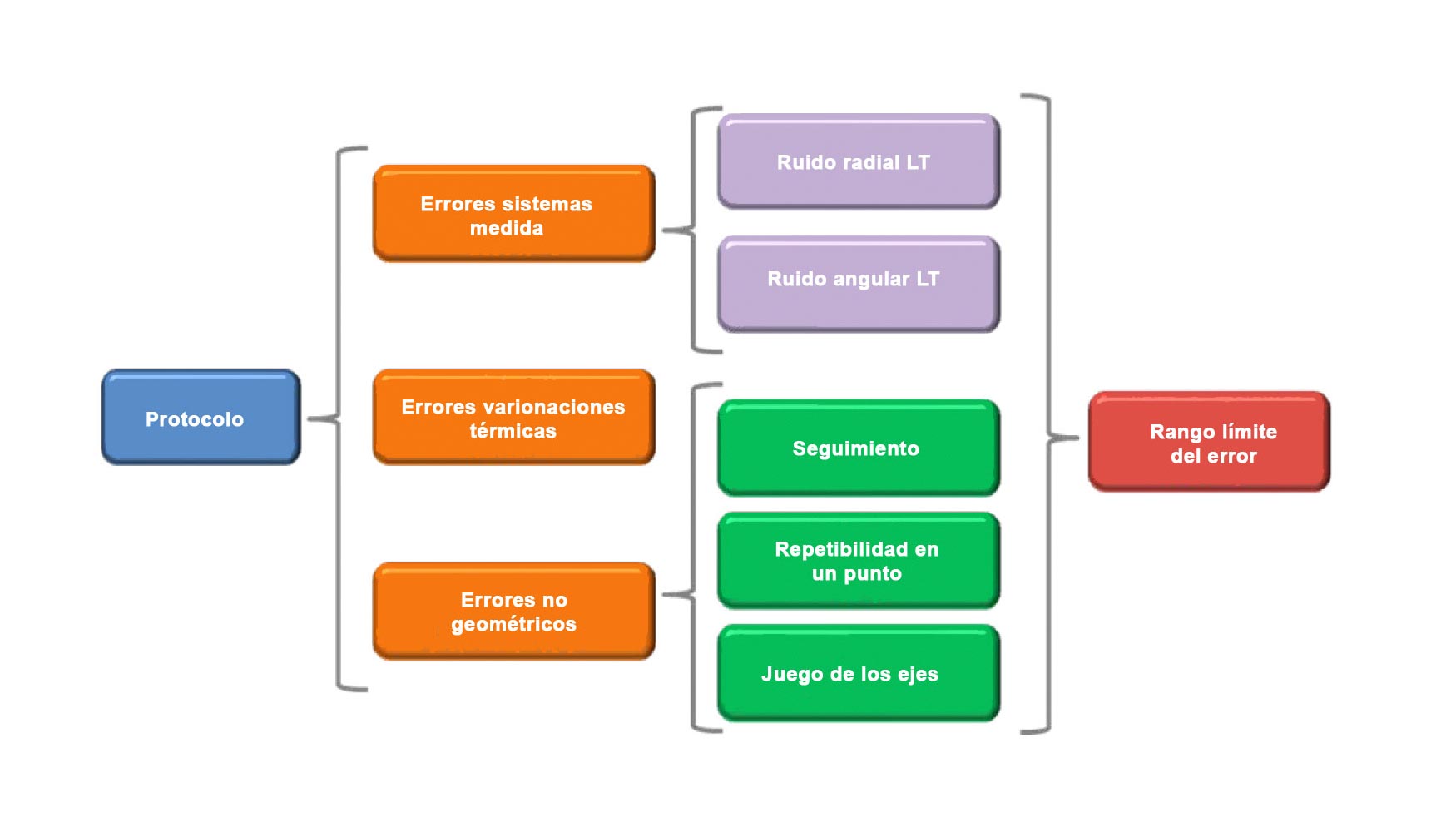
De todas las fuentes de error de una máquina-herramienta (MH) el proceso de identificación de parámetros, base de la verificación volumétrica, minimiza la influencia de los errores geométricos y cinemáticos de la máquina; siendo necesario estimar la influencia del resto de errores con objeto de evitar problemas de overfitting. La estimación de este valor se obtiene a partir de la aplicación de un protocolo de verificación en el que se estudia la influencia de los errores provenientes del sistema de medida, los errores no geométricos y el tiempo de calentamiento y medición mínimo y máximo admisible como consecuencia de las variaciones térmicas [11].
El software desarrollado posee una interfaz de uso intuitivo para el usuario a partir de la cual introducir la información del ensayo y calcular los errores de: repetibilidad, seguimiento y juego de la máquina. Este también permite la representación la evolución de la temperatura a lo largo del tiempo en el que se ha realizado la captura de datos utilizados en la verificación. La captura de datos se realiza con el propio laser utilizado para la verificación con ayuda de un generador de código CNC que permite en lenguaje ISO generar la distribución de puntos con la que determinar cada uno de estos errores.
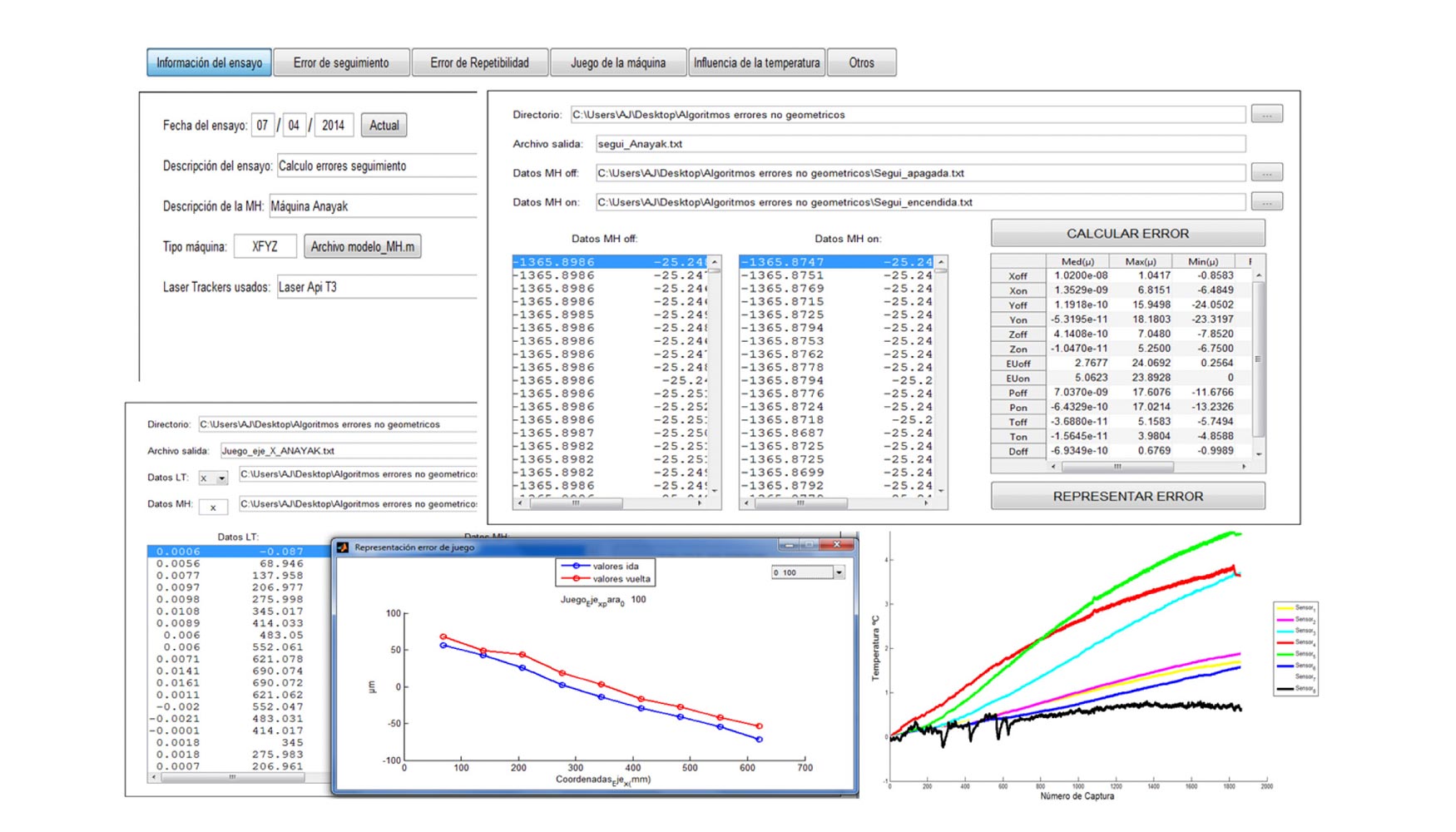
Tras el análisis de los resultados que esta herramienta proporciona se obtiene el tiempo de calentamiento de la máquina, se estima la variación máxima admisible de temperatura durante la medición, junto con el error de juego de la máquina y la influencia del error de seguimiento y repetibilidad. De esta manera se obtiene un rango de error; a partir del cual se considera que el proceso de optimización con el que se obtienen las funciones de aproximación de cada uno de los errores está introduciendo en las mismas la influencia de fuentes de error no geométricos. Del mismo modo, también se obtienen las condiciones de medición más favorables para la captura de datos.
3.2 Caracterización y compensación de los errores geométricos de una máquina-herramienta
El software desarrollado permite realizar el cálculo de los errores en función de la secuencia de medición que mejor se adecue a la técnica de identificación [8, 12]. Este está formado por un conjunto de seis módulos independientes cuyas salidas se integran con el resto de funciones del programa de verificación; formando un conjunto de algoritmos robusto y a la vez flexible que permiten realizar la verificación volumétrica de los errores geométricos tanto de los ejes lineales como giratorios de una MH:
- Módulo generación programas control numérico.
- Módulo generador modelos cinemáticos.
- Módulo generación archivo configuración.
- Módulo verificación volumétrica.
- Módulo representación resultados.
- Módulo compensación.
El primer módulo está formado por un conjunto de algoritmos que permite discretizar el volumen de trabajo en función de los errores a caracterizar en forma de malla uniformemente distribuida, nube aleatoria de puntos, zonas de concentración de puntos y diagonales. Del mismo modo, el software define la secuencia de medición en función de la consideración o no del error de juego en la verificación, extensión de programa CNC que admite el control de la máquina, tiempo de parada entre puntos necesario para su correcta medición, etc.
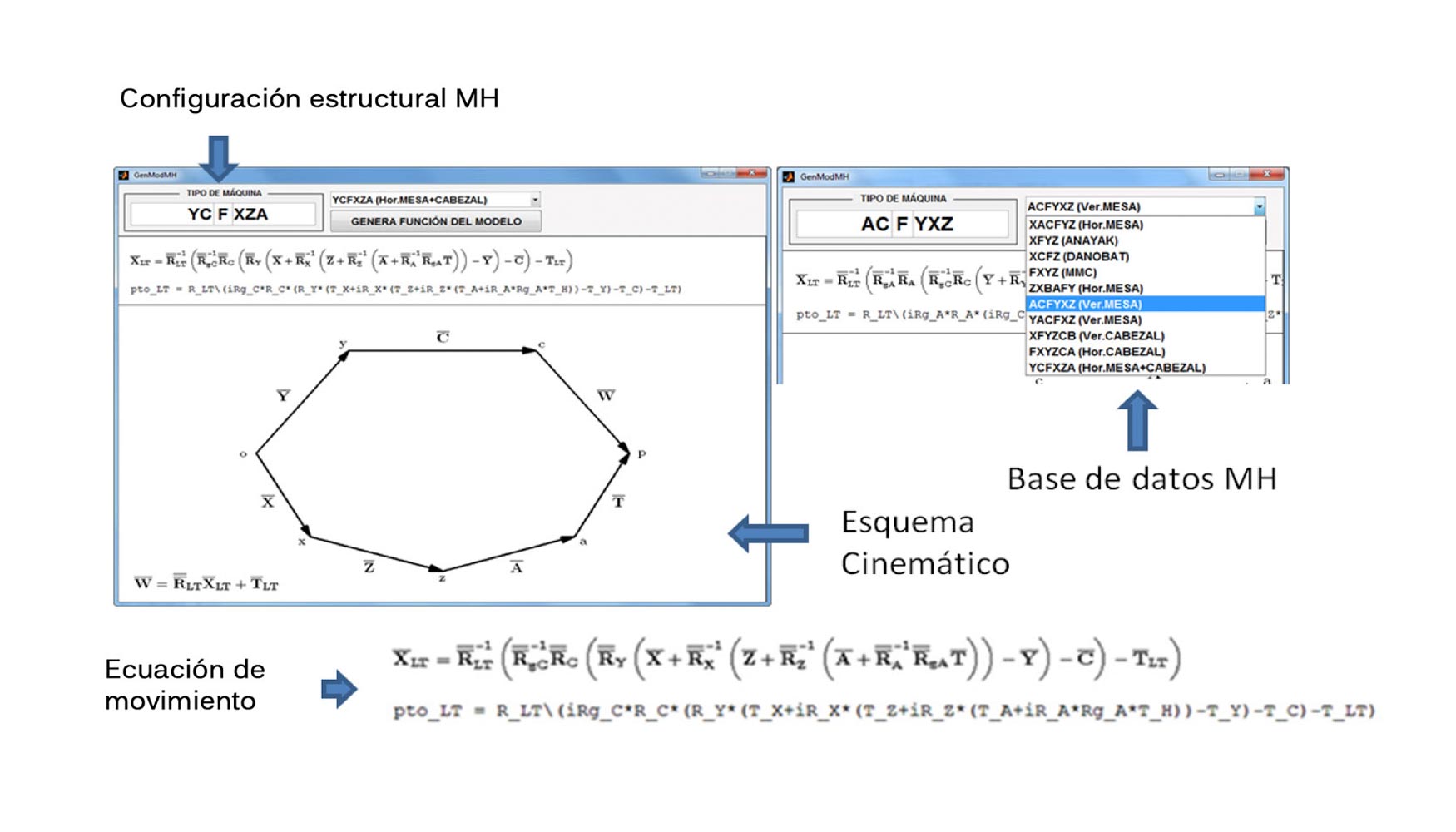
El segundo módulo, el módulo generador de modelos cinemáticos, se encarga de obtener a partir de la configuración estructural de la máquina el modelo cinemático de la misma. La estructura de la máquina quedará determinada por la combinación de los diferentes elementos estructurales guías, articulaciones, husillos, etc. La estructura cinemática que conforman estos componentes se puede modelar mediante una cadena cinemática que simboliza su flujo de movimientos a través de un esquema cinemático, y un modelo matemático que relaciona a través de la ecuación de movimiento de la máquina los diferentes elementos estructurales entre sí. De esta manera es posible obtener la posición en coordenadas cartesianas de la punta de la herramienta con respecto a la pieza (LT) en función de varios factores: la posición nominal programada, la posición de la punta de la herramienta con respecto al sistema de referencia de la máquina (offsets) y los errores geométricos de los ejes; ocupando durante la verificación el laser tracker el lugar correspondiente a la pieza y el reto-reflector el lugar correspondiente a la herramienta.
La obtención del modelo cinemático y ecuación de movimiento de cada MH requiero de un proceso detallado y complejo para realizarse de manera manual. La aplicación desarrollada permite al usuario obtener el modelo cinemático de cualquier MH, así como la ecuación de movimiento de esta con la incorporación del sistema de medida.
Tras obtener el modelo cinemático de la máquina y definir qué zonas del volumen de trabajo de la misma se van a analizar, el siguiente paso viene definido por la determinación de la estrategia de medición de la máquina. Esta vendrá determinada por la configuración estructural, control y tipos de ejes de movimiento de la máquina, espacio disponible para la distribución del laser tracker y secuencias de identificación (caracterización) de los errores definida por el usuario. Las diferentes estrategias de medición a utilizar están directamente relacionadas con las estrategias de verificación a utilizar. Los diferentes métodos y estrategias de verificación se basan en la optimización por fases en función de:
- Fases de optimización que constituyen el proceso completo de identificación de errores.
- Ejes de movimiento al que pertenecen los errores geométricos a identificar en cada fase.
- Tipos de errores geométricos y cinemáticos a identificar provenientes de cada uno de los ejes de movimiento incluidos en cada fase de la verificación.
- Funciones de regresión, grado y valores iniciales a emplear en la identificación de los errores en función de su comportamiento físico.
- Características propias del modelo cinemático de cada máquina: offsets MH, offset herramienta, etc.
- Técnicas de mejora de precisión de los puntos capturados mediante multilateración y auto-calibración de LTs.
- Criterios de convergencia del proceso de identificación utilizados.
Como ejemplo de las diferentes secuencias de medición en función de la estrategia seleccionada, se muestra en la figura 6 la captura de datos para la verificación de una máquina con configuración XCFZ. En la imagen de la izquierda se observa como el laser tracker rota en torno al eje del plato giratorio 360º; mientras que en la imagen de la derecha el giro en torno a C se encuentra limitada por el cadenado de la máquina. Del mismo modo, en el primer caso (figura 6 izquierda) los recorridos de los ejes lineales son reducidos, a diferencia de lo que ocurre en el segundo caso (figura 6 derecha). Esta figura muestra como la estrategia de verificación y requerimientos del cliente determinarán los montaje a realizar y estrategias de medición a utilizar [12].
Por ejemplo, el montaje de la derecha permite calcular la influencia de los errores geométricos provenientes de los ejes lineales en mayor rango XZ y menor C, mientras que el montaje de la izquierda permite la caracterización de los errores en todo el rango del eje de rotación C y menor rango XZ. Del mismo modo, el montaje de la izquierda puede utilizarse para obtener solamente los errores del eje de rotación C y el montaje de la derecha para obtener los errores de los ejes lineales; para conseguir una mayor rango volumen de verificación en todo el volumen de la máquina sería necesario realizar una caracterización-identificación combinada empleando ambos montajes [12].

Las diferentes alternativas que constituyen las posibles estrategias de verificación se han unificado en una única herramienta Módulo generación archivo configuración. Lo que permite al usuario realizar la caracterización-identificación de los errores geométricos de una misma máquina desde diferentes enfoques gracias a la gran flexibilidad de la aplicación.
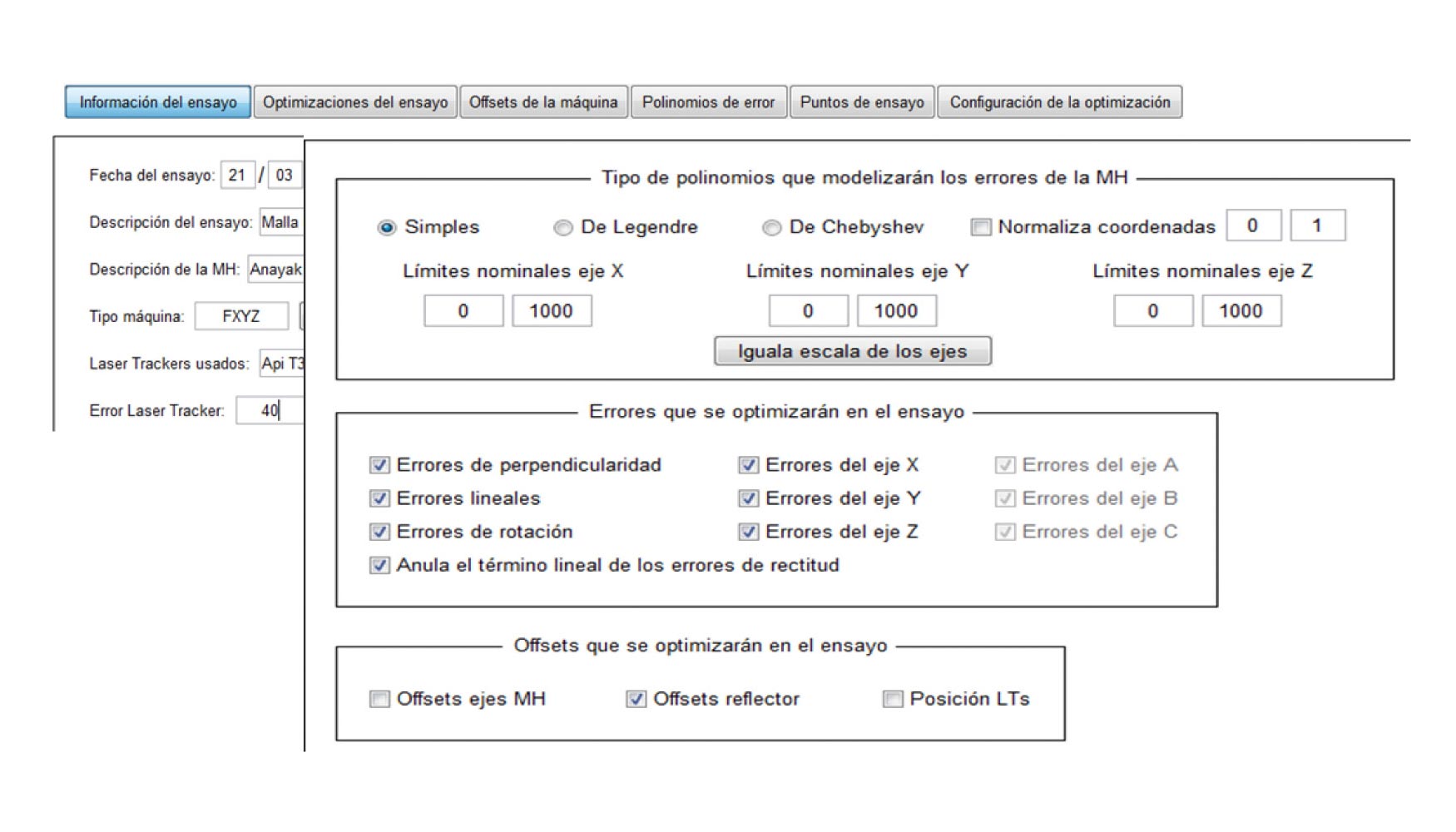
Una vez configurada por el usuario la estrategia de verificación el módulo 4, Modulo verificación volumétrica, es el encargado de transcribir e introducir esta información en los diferentes algoritmos encargados de realizar la identificación y caracterización de cada uno de los errores geométricos presentes en cada una de las fases que constituyen la estrategia de verificación.
El conjunto de algoritmos utilizados para caracterizar-identificar cada uno de los errores utiliza técnicas de optimización mediante el uso de los algoritmos de Levenberg-Marquardt. El proceso de identificación se basa en la variación de los coeficientes de un vector de parámetros a partir de una función objetivo. Este está formado por los coeficientes de cada error a caracterizar en función de las estrategias definidas (figura 8).
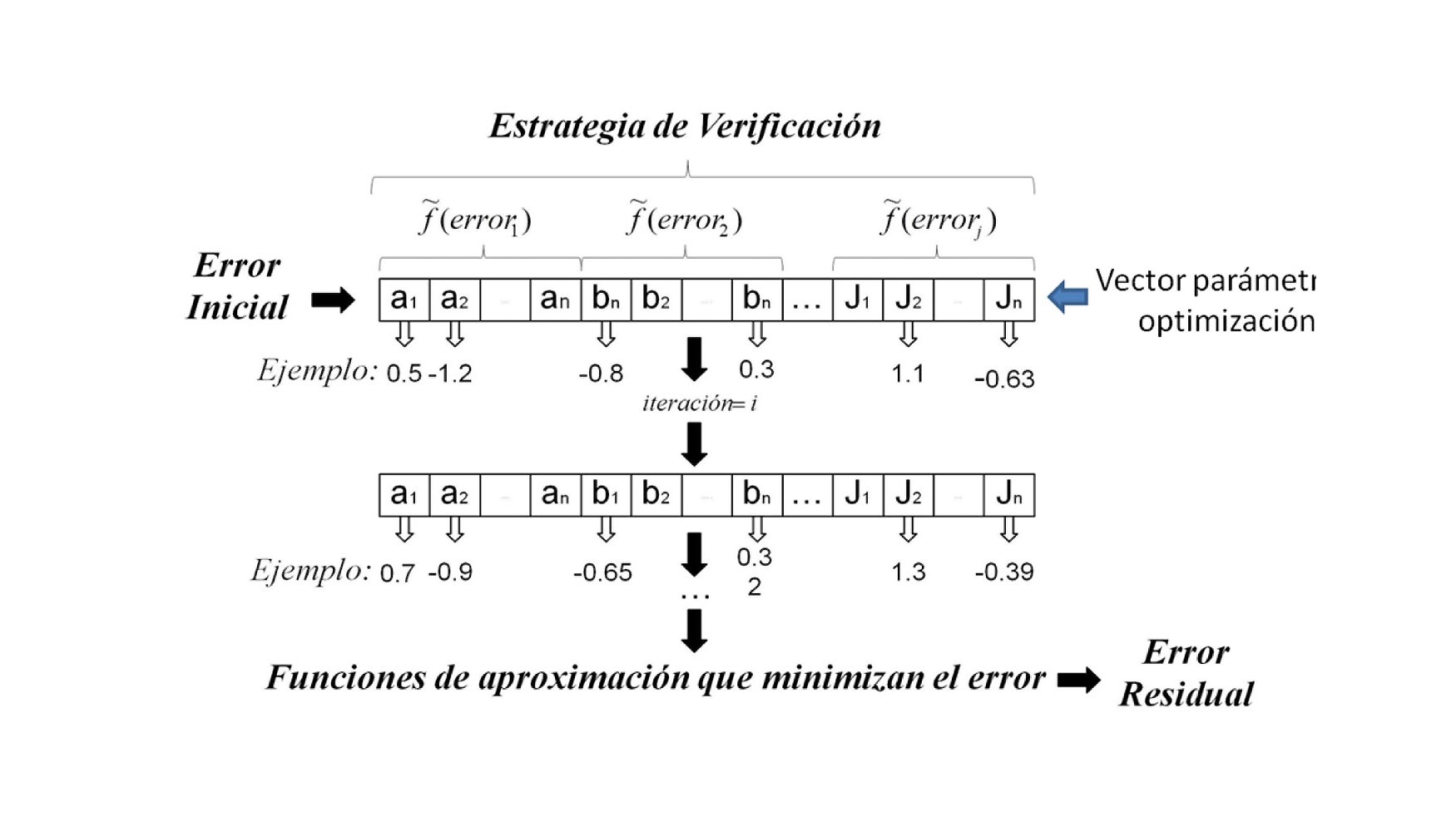
Cada uno de los coeficientes ai..an, bi…bn, etc son evaluados en cada iteración a través de las funciones de regresión de cada uno de los errores; al final del proceso de optimización se obtiene para cada error analizado una función ͠ƒ(j)≈ƒ(j) con j = x, y, z, a, b, c variables de dependencia del error geométrico.
Las funciones de regresión a emplear en la caracterización-identificación de los errores geométricos están relacionadas con el comportamiento físico de los mismos [7, 8]. En el caso de los errores geométricos provenientes de un eje lineal las funciones de regresión a emplear son:

Siendo n el grado de la función aproximada, θi el peso asociado a cada polinomio de Chebyshev de orden i y Ti(x) el polinomio de Chebyshev de orden i. Los polinomios de Chebyshev tienen la forma:
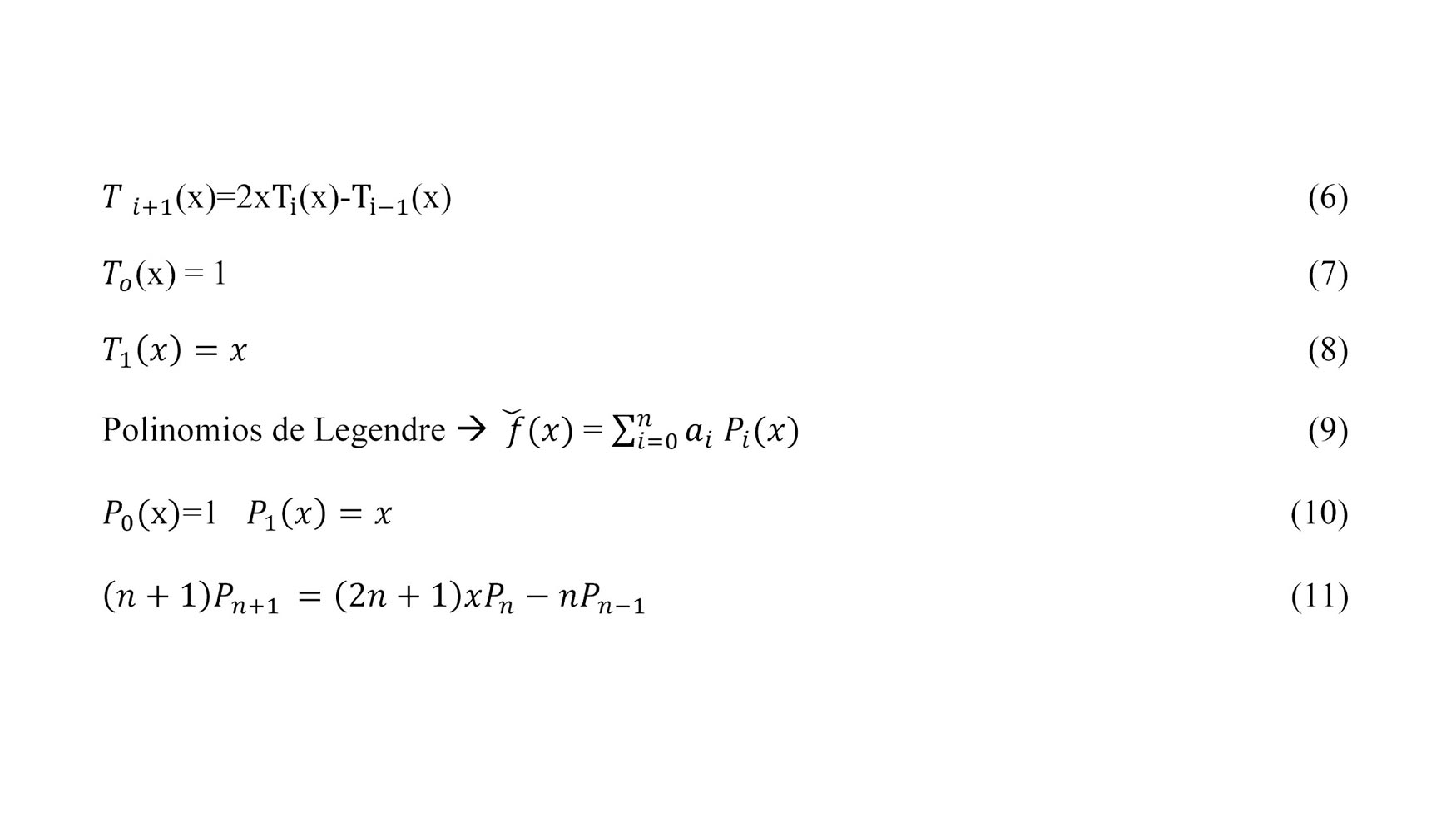
En el caso de los errores geométricos provenientes de un eje de rotación [12], el comportamiento periódico de los mismos no puede ser caracterizado mediante las funciones de los ejes lineales. Por lo que es necesario utilizar funciones de regresión que permitan caracterizar este comportamiento periódico, series de Fourier.
Series de Fourier.
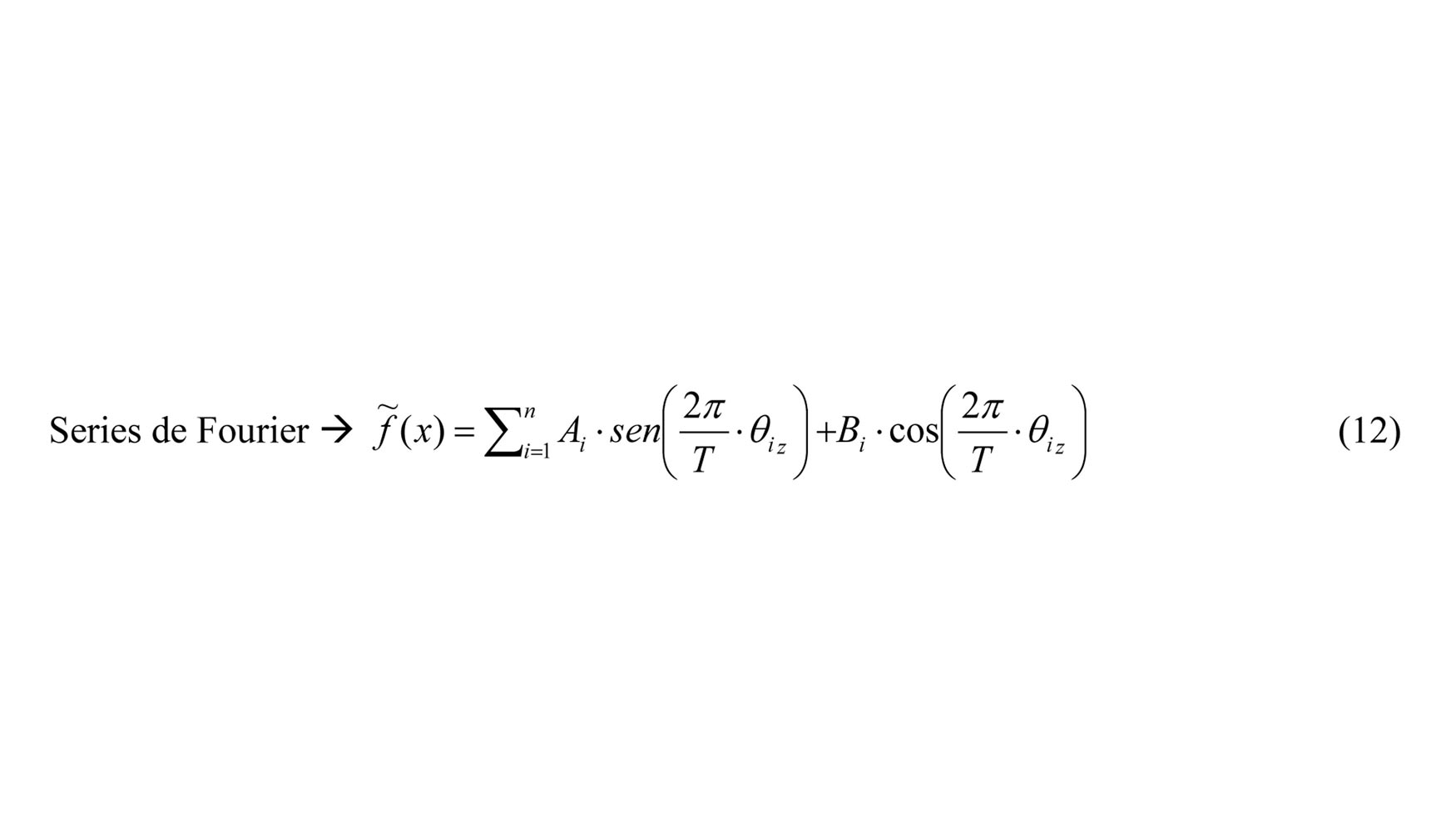
Donde los coeficientes a caracterizar son A1… An, B1…Bn y la variable de dependencia es θ.
La adecuación de las funciones de aproximación obtenidas está directamente relacionada con la precisión de los puntos capturados y la precisión de la matriz de roto-traslación entre sistema de coordenadas MH y sistema de coordenadas de referencia (LT). La mejora en la precisión de los puntos capturados se consigue mediante la aplicación de técnicas de multilateración, mientras que el ajuste entre los distintos sistemas de coordenadas se obtiene mediante la aplicación de técnicas de auto-calibración.
El modulo de verificación volumétrica permite la utilización de ambas técnicas de mejora de precisión como fase previa a la obtención de los errores geométricos de la máquina. Las técnicas de auto calibración y multilateración implementadas son:
- Intersección de esferas mediante ajuste por mínimos cuadrados.
- Trilateración.
- Tetralateración.
La técnica de intersección de esferas se basa en la resolución analítica [9]. El laser tracker proporciona las coordenadas de un punto medido en coordenadas esféricas (r, θ, Φ). La mayor contribución a la incertidumbre de medida la realizan las coordenadas θ y Φ de los puntos medidos. Al despreciar esta información solamente nos quedamos con la componente radial r por lo sabemos que el punto medido se encuentra en la superficie de una esfera con centro el sistema de coordenadas del laser tracker y radio r. Si medimos este punto desde tres posiciones de laser tracker más obtenemos un sistema de ecuaciones con la forma:
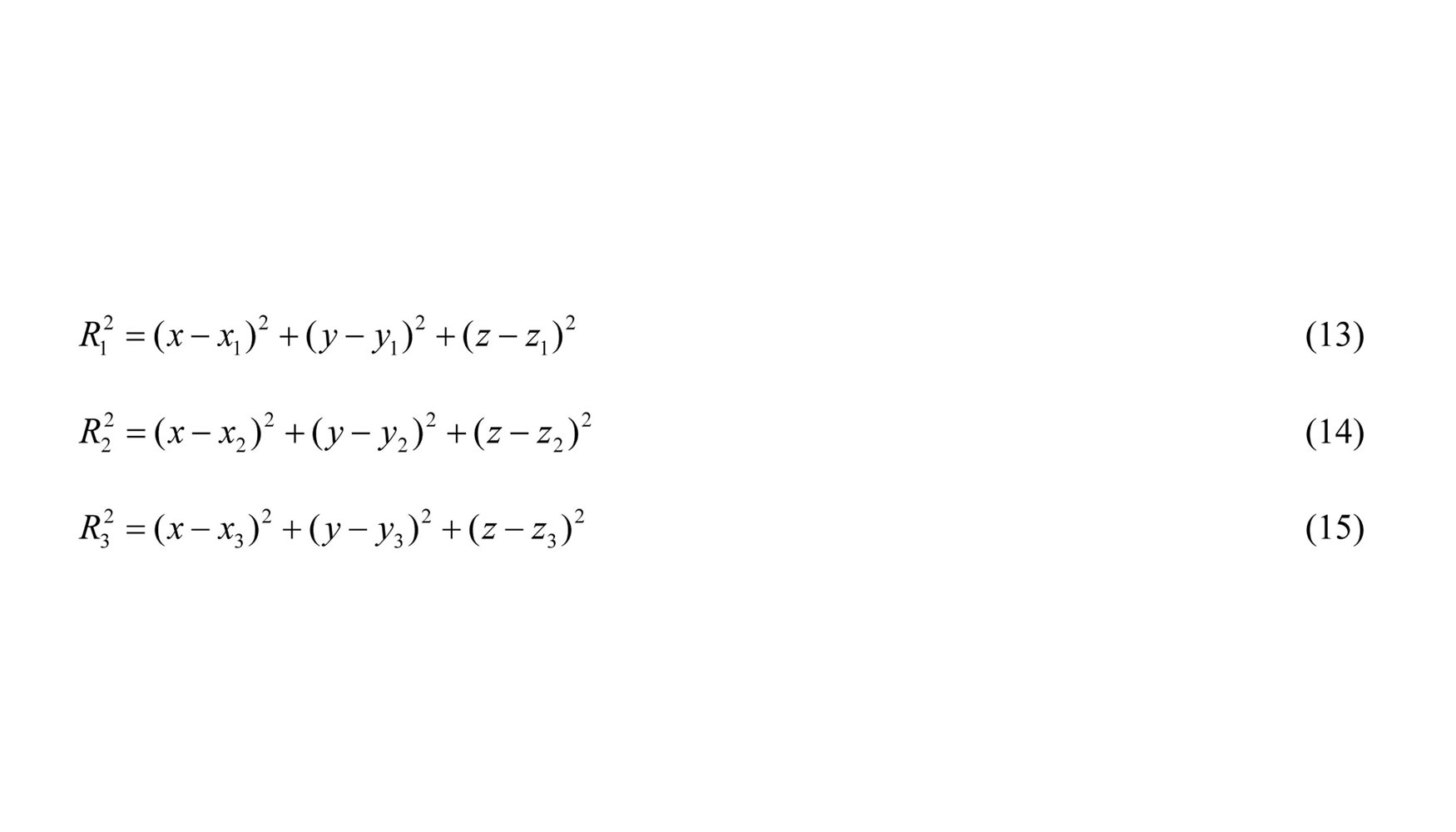
A diferencia de la multilateración mediante intersección de esferas, la multilateración mediante la técnica de trilateración obtiene de manera conjunta el posicionamiento relativo de los LTs, autocalibración, y los coordenadas de los puntos multilaterados [9, 10]. Esta técnica se basa en un proceso iterativo de identificación de parámetros mediante la minimización de la diferencia entre las distancias medidas por cada uno de los LTs. Siendo (Xi Yi Zi) las coordenadas de posicionamiento del láser ith y di la distancia entre laser y reflector, los puntos multilaterados (xj, yj, zj) y posición LTs se obtiene mediante la minimización de ecuación 16.
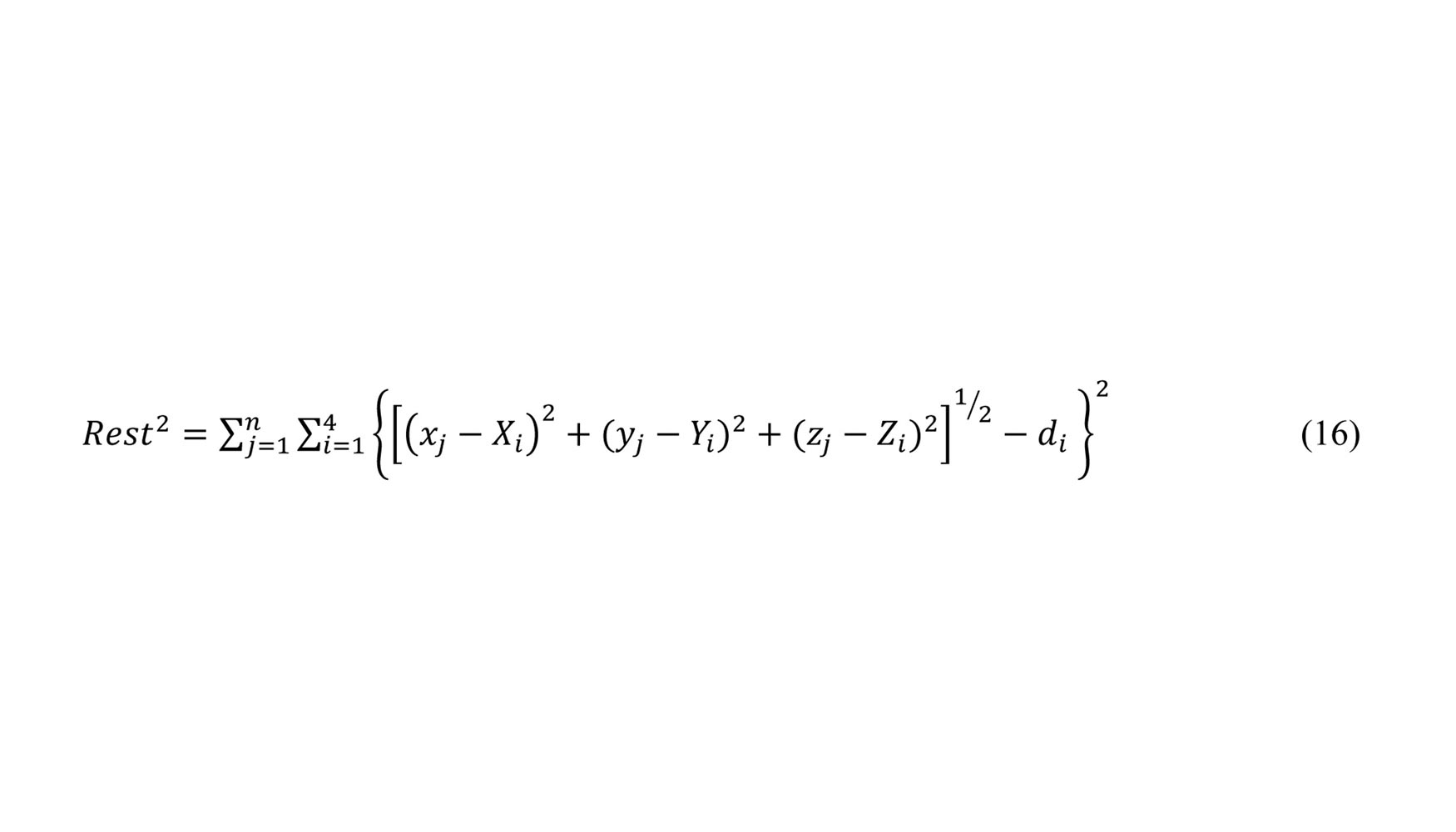
Una vez obtenidas las funciones de aproximación de los diferentes errores geométricos junto con toda la información que proporciona el módulo de verificación, se desarrollan una serie de algoritmos que constituyen el Módulo de Representación de esta aplicación. Estos algoritmos son los encargados de proporcionar información del proceso de caracterización de errores, evolución de la caracterización, funciones de aproximación obtenidas, diagrama vectorial y mapa de colores anterior y posterior a la compensación de errores, etc.
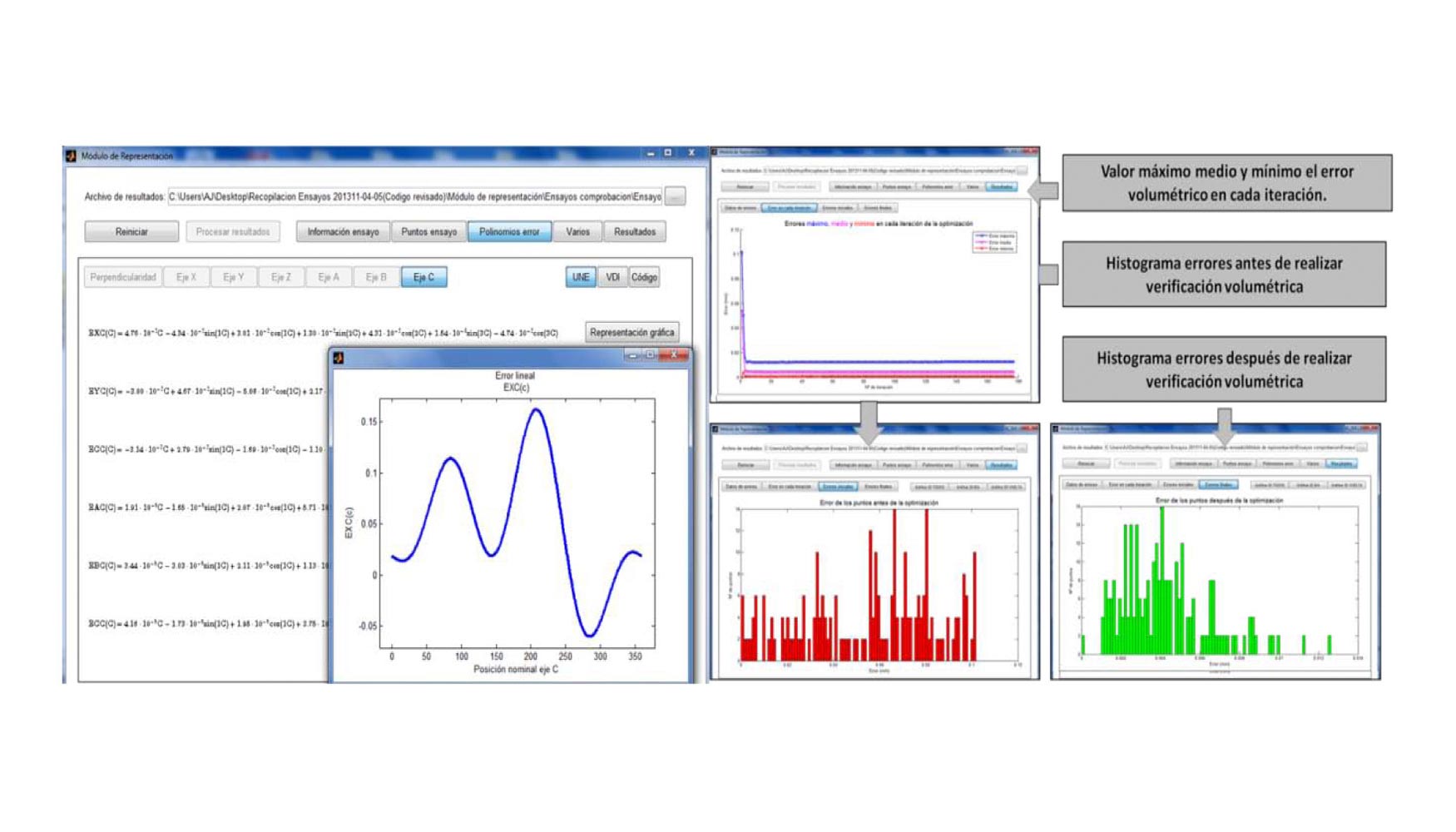
El último módulo que forma parte de la aplicación desarrollada es el Módulo Compensación. Este módulo está formado por un conjunto de algoritmos encargados de obtener un nuevo programa de CN a partir las funciones de caracterización, obtenidas en la verificación, y el modelo cinemático de la máquina. Los puntos nominales son afectados en el modelo por las funciones de regresión obtenidas en la verificación; este proporciona como salida otros puntos diferentes los cuales llevan asociados otro error diferentes a los nominales. Mediante un proceso de minimización a través de Levenberg Marquard se obtienen las nuevas coordenadas que minimizan el error en el punto. Esta herramienta permite validar mediante la utilización de sistemas de medida externos como el interferómetro laser, o bien mediante la remedición mediante LT de los puntos utilizados en la verificación u otros puntos de control la adecuación de las funciones de aproximación obtenidas mediante las funciones de regresión.
4. Ensayos
Las distintas opciones proporcionadas por el software desarrollado han sido evaluadas y validadas tanto mediante la realización de ensayos sintéticos como reales. En este artículo se presentan los resultados de verificación de un centro de mecanizado Zayer TB 5000 con configuración XFYZCB, donde la pieza se mueve asociada con el eje X respecto de la bancada F, y la herramienta se mueve asociado a los ejes lineales YZ y los ejes de rotación C (giro respecto Z) y B (giro respecto Y).
Las necesidades del cliente se centraban en la mejora de precisión de los ejes linéales; por lo que el modelo cinemático de la máquina se reduce a una MH con configuración estructural XFYZ. El esquema cinemático y ecuación de movimiento de la estructura de la máquina a verificar se obtuvo mediante el Módulo generador modelos cinemáticos; relacionando las coordenadas de los puntos medidos con el laser tracker y las coordenadas nominales de la máquina a través de los errores geométricos de la misma.
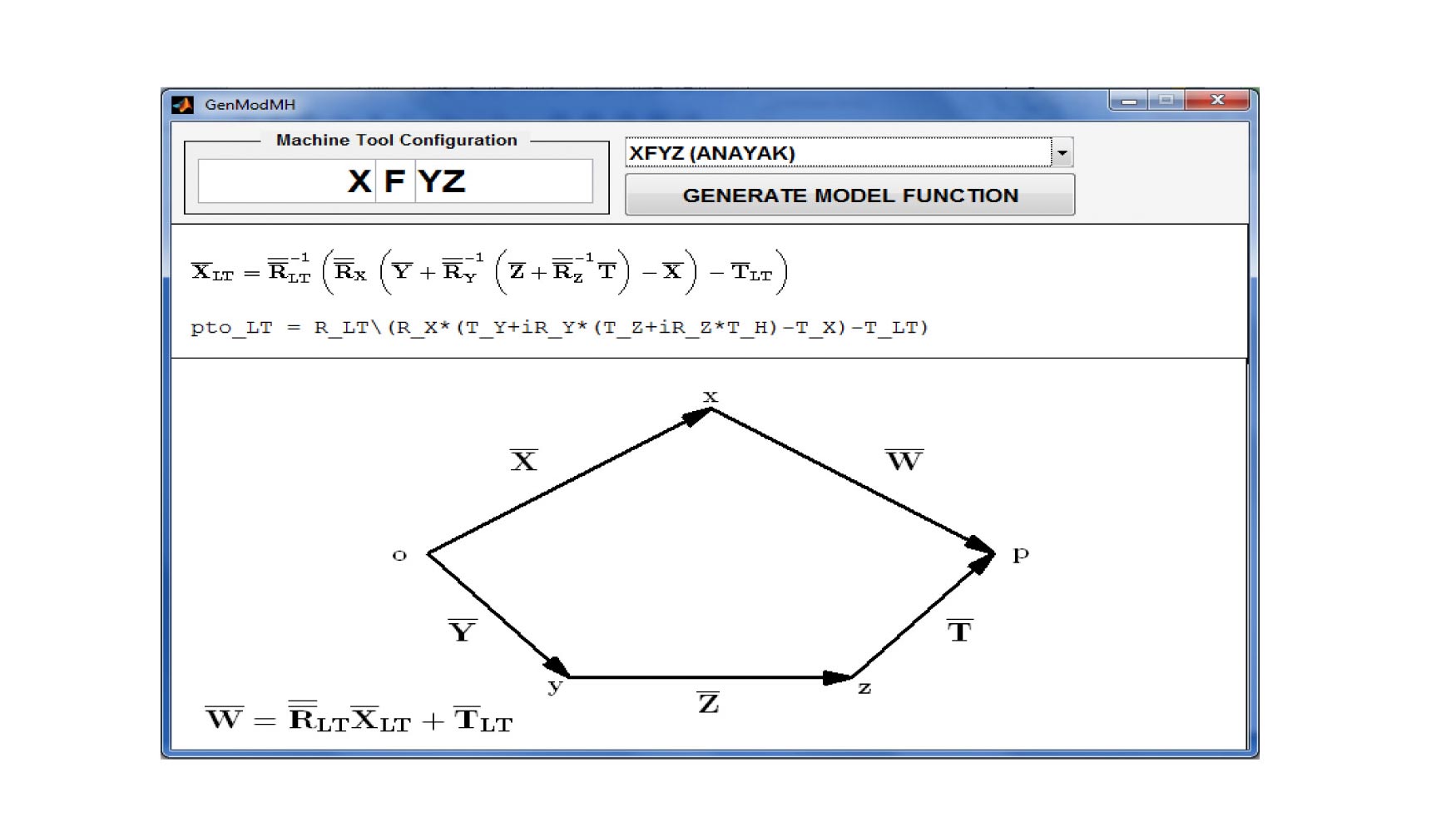
El vector X̅LT representa las coordenadas de un punto nominal P (x, y, z) medido con el laser en función de la posición del LT y errores geométricos de la máquina.

Donde εx(k), εy(K) y εz(k) son los errores de rotación del eje k = x, y, z; δk(k) es el error de posición del eje k = x, y, z; δk(j) con k ≠ j es el error de rectitud en la dirección k; y εxy, εxz, εyz son los errores de perpendicularidad. ̅TTL y ̅RTL representan el vector de traslación y matriz de rotación que relacionan LT con MH.

Uno de los principales objetivos del cliente era conocer y compensar el mayor volumen de trabajo de la máquina posible. Motivo por el cual se desecho la utilización de un retro reflector SMR tradicional; sustituyendo este por la utilización de un retro reflector motorizado Active Target. Mediante la utilización de este nuevo reto reflector se consiguieron distribuir puntos para la verificación en el 96,59% del volumen de trabajo de la máquina.
Otra de los inquietudes del cliente era conocer la calidad del la compensación actual introducida en el control de la máquina en cada eje y la capacidad de mejora de la misma en todo su volumen de trabajo. Al poder proporcionar la verificación volumétrica una compensación matemática, no física, de los errores geométricos de la máquina, esta puede aplicarse sobre una máquina ya compensada. Sin embargo, el comportamiento y alcance del proceso de identificación quedará supeditado a la forma del error residual proporcionada por la corrección anterior.
Las características del ensayo realizado quedan reflejadas en un ficha tipo, complementada a partir de los resultados del Módulo de representación que permite de manera rápida conocer el estado inicial y final del proceso de verificación. Un extracto de esta ficha se presenta a continuación:
- Configuración estructural verificada: XFYZ.
- Volumen de trabajo XFYZ: 0 ≤ X ≤ 5050, 0 ≤ Y ≤ 2050, 0≤ Z ≤ 750, C = 0, B = 0;
- Volumen de trabajo verificación: 0 ≤ X ≤ 5000, 0 ≤ Y ≤ 2000, 0 ≤ Z ≤ 750, C = 0, B = 0;
- Discretización volumen de trabajo: Malla ida-vuelta con sobre-pasamiento.
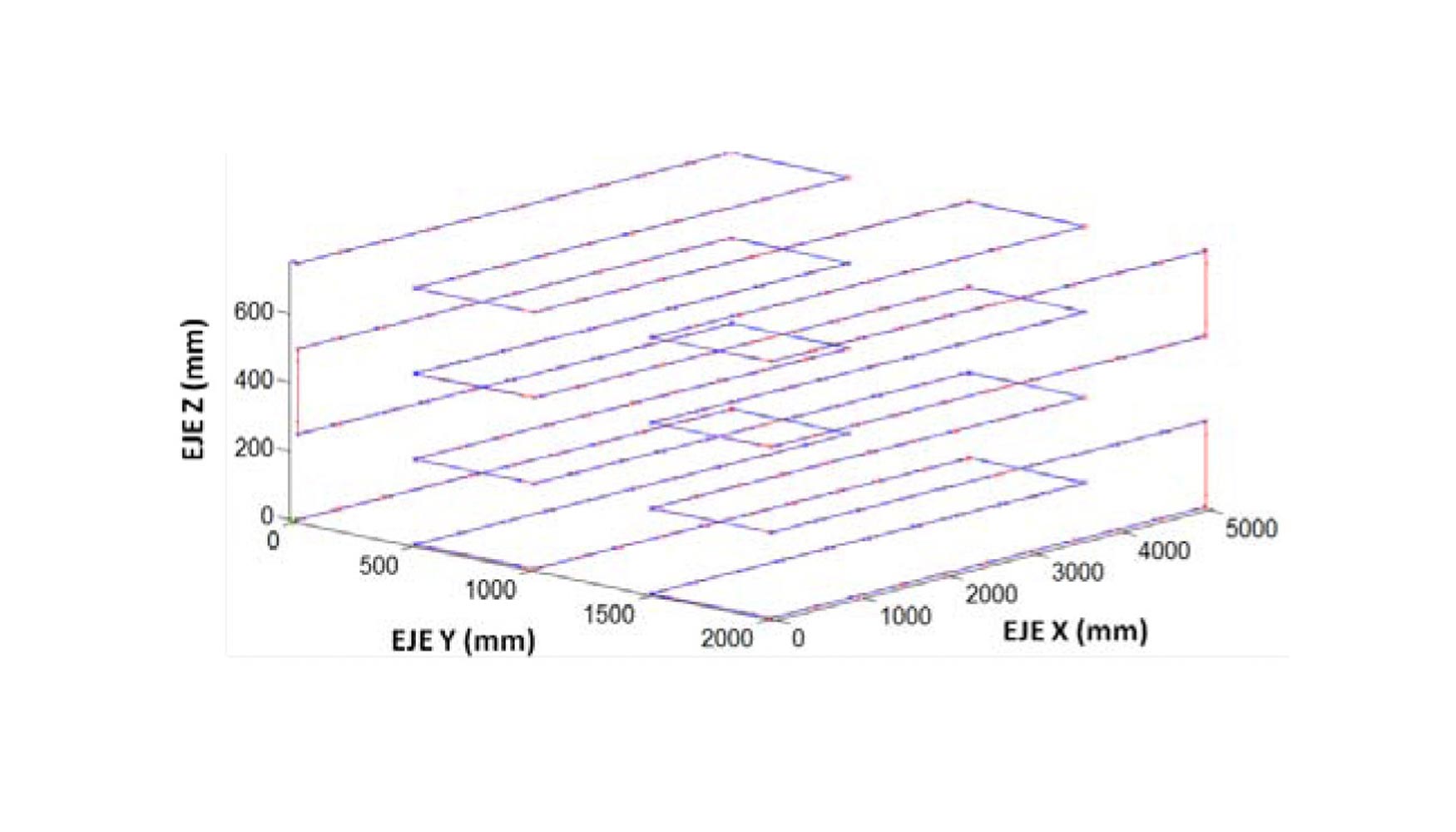
Malla verificación utilizada.
- Número puntos medición: 483.
- Número puntos verificación: 438 (219 de ida y 219 de vuelta)
- Sistema de medida utilizado: Laser Tracker Api T3 con reflector Active Target.
- Tiempo de parada en punto estable: 4 segundos.
- Extensión fichero CNC generado: *.i
- Tabla compensación máquina-herramienta: ON.
- Decalaje sistema verificación: x = -916,053 mm, y = 4262,3777 mm, z = 1726,4019 mm.
- Tiempo captura de datos: 1 hora 30 minutos.
La estrategia de verificación utilizada en el proceso de verificación se basó en un proceso de caracterización en 2 fases. La primera fase se encargó de la caracterización de los errores de perpendicularidad y rectitud de los tres ejes lineales; mientas que el segundo se centro en la caracterización de los errores de rotación. El análisis de los datos capturados para la verificación (figura 11) muestra en error volumétrico medio de 83 μm, un error máximo en módulo de 197 μm y un error mínimo de 10 μm. La representación de los errores de la máquina en forma de mapa de colores permite observar las zonas de concentración de errores. En este mapa se observa como las zonas de mayor concentración de errores se encuentran en los extremos de la máquina; siendo la zona central (la más utilizada) la que menor error presenta.
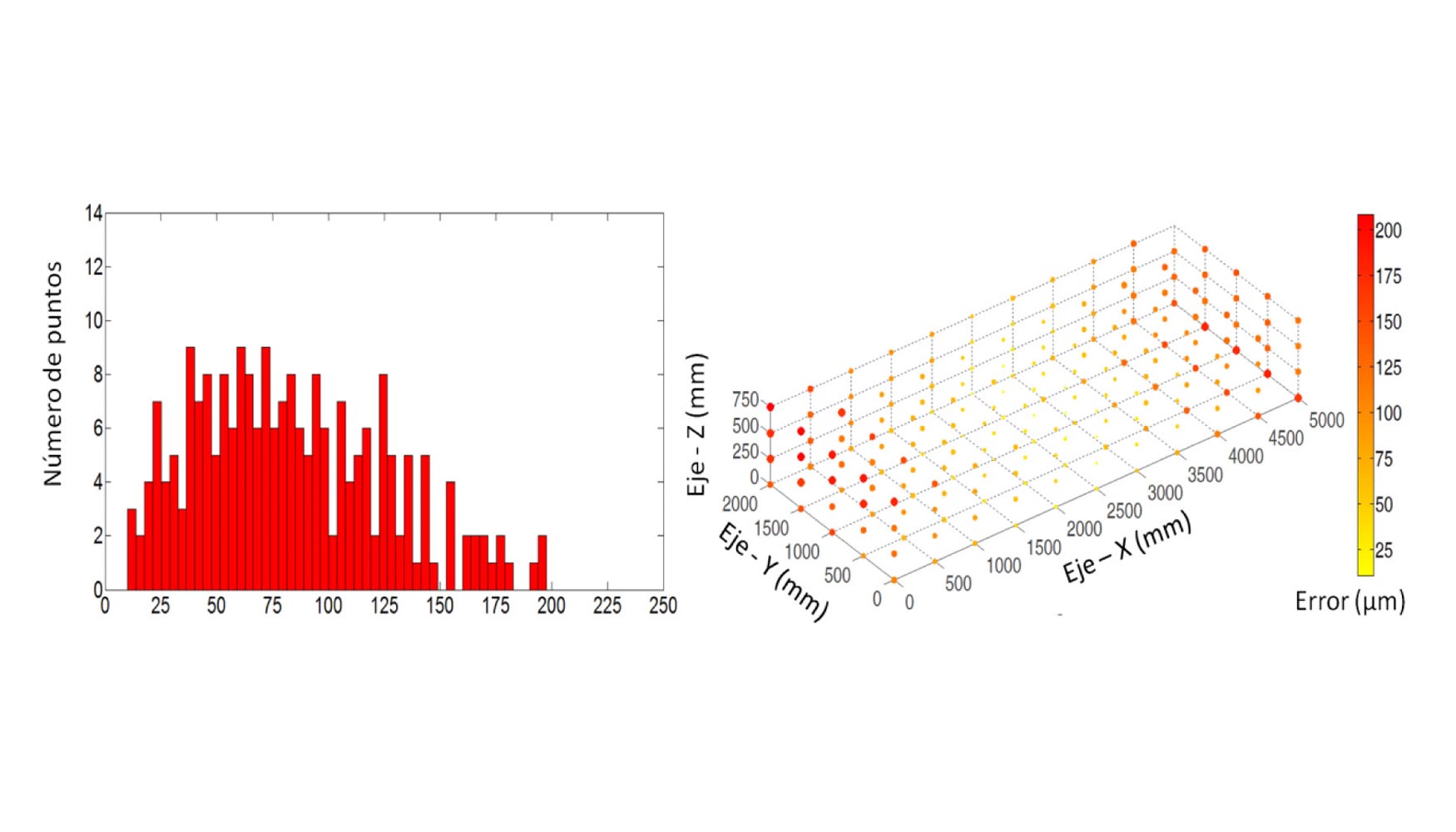
A partir de los resultados obtenidos mediante el módulo de verificación y tras la realización del post-procesado y remedición del programa de CN mediante el módulo de compensación. Los resultados muestran un reducción del error volumétrico medio a 47,1 μm, un error máximo en módulo de 105,4 μm y un error mínimo de 4,5 μm; consiguiendo una reducción del error volumétrico medio del 43,25%. La variación de temperatura ambiente durante la captura de datos y la medición de la malla de verificación una vez compensada ha sido controlada; observándose una variación máxima de 1 °C durante ambos procesos.
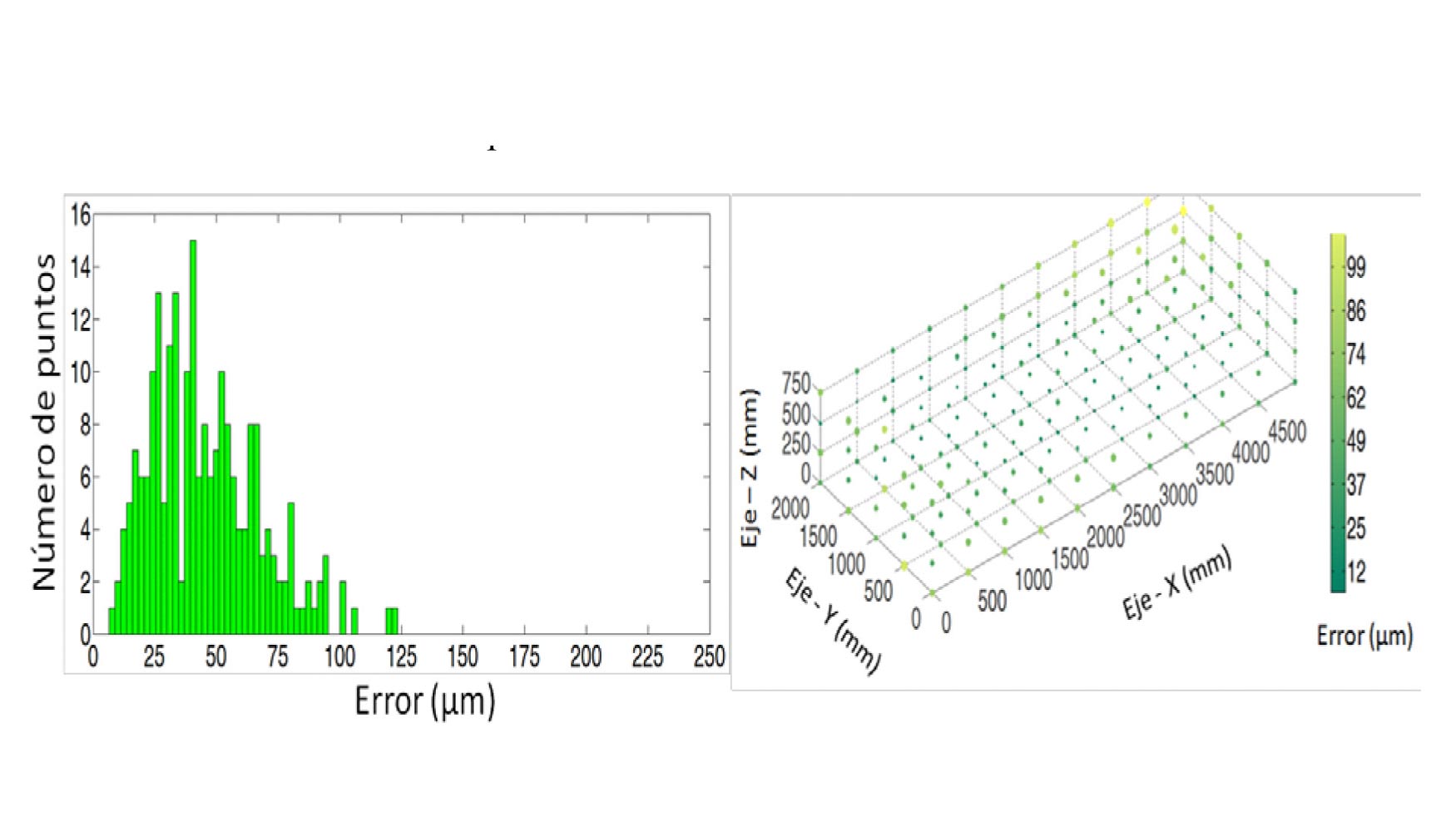
Esta misma máquina también fue verificada manteniendo la misma estrategia de verificación con la compensación de la máquina desactivada. Lo que generó que el error volumétrico de la máquina ascendiera de 83 a 113 μm, el error máximo 197 μm a 246 μm y el error mínimo asciende de 10 a 15 μm. Tras realizar la compensación de la máquina a partir de las funciones de aproximación obtenidas durante la verificación el error volumétrico de la máquina se reduce un 49,1%.
Otra de las estrategias utilizadas en la verificación de esta máquina fue la utilización de técnicas de multilateración mediante trilateración simultánea como paso previo a la verificación y la multilateración mediante multi-posición con un solo LT.
Los tres laser tracker se encuentran midiendo simultáneamente el mismo reto-reflector SMR. Por lo que el volumen de trabajo a verificar con este retro-reflector está limitado por el ángulo de visión que tiene cada uno de los LT con el ángulo de ±30º del reflector. El comportamiento de la multilateración viene dado por la distribución espacial de los LT, características de medición, etc, [9, 10]. La verificación realizada mediante esta estrategia consigue reducir el error volumétrico medio de la zona verificada un 44%; porcentaje superior al conseguido con la utilización de un solo LT.

Conclusiones
A partir de las técnicas y procedimientos desarrollados se puede realizar una compensación del efecto conjunto de los errores geométricos en función de la estrategia de verificación a definir por el usuario, la configuración estructural de la máquina, tipo y comportamientos de los errores geométricos de la misma.
Los ensayos realizados muestra que la reducción del error volumétrico medio entorno al 50%; consiguiendo verificar casi el 97% del volumen de trabajo de la máquina mediante un solo laser tracker con retro-reflecto motorizado. La utilización de tres laser tracker permite la aplicación de técnicas de multilateración; estando el alcance de las mismas relacionadas con la distribución y características de los equipo.
Bibliografía
[1] Slocum, A., (1992), Precision Machine Design, Prentice Hall.
[2] Schwenke, H.; Knapp, W.; Haitjema, H.; Weckenmann, A.; Schmitt, R.; Delbressine, F. (2008). “Geometric error measurement and compensation of machines – An update”. CIRP Annals-Manufacturing Technology. vol. 57, p.p. 660-675.
[3] Ramesh, R.; Mannan, M.A., Poo, A.N; (2000). ‘Error compensation in machine tools—a review Part II: thermal errors’. International Journal of Machine Tool & Manufacture. vol. 40, p.p. 1257-1284.
[4] Delbressine, F.L.M.; Florussen, G.H.J.; Schijvenaars, L.A.; Schellekens, P.H.J, (2006) ‘Modelling thermomechanical behavior of multi-axis machine tools’. Precision Engineering. vol.30, p.p. 47-53.
[5] Bryan, J., (1990), ‘International Status of Thermal Error Research (1990)’, CIRP Annals, Vol. 39, No. 2, pp. 645-656.
[6] Ni, J., (1997), ‘CNC Machine Accuracy Enhancement through Real-Time Error Compensation’, Journal of Manufacturing Science and Engineering, Vol. 119, No. 4B, pp. 717-725.
[7] Aguado, S.; Samper, D.; Santolaria, J.; Aguilar, J.J. Identification strategy of error parameter in volumetric error compensation of machine tool based on laser tracker measurements. International Journal of Machine Tools & Manufacture, (2012), Vol. 53, p.p. 160-169.
[8] Aguado, S.; Samper, D.; Santolaria, J.; Aguilar, J.J. Towards an effective identification strategy in volumetric error compensation of machine tools. Measurement Science and Technology, (2012), Vol.23, 12 pp.
[9] Aguado S, Santolatira J, Samper D, Aguilar J. J. Influence of measurement noise and laser arrangement on measurement uncertainty of laser tracker multilateration in machine tool volumetric verification. Precision Engineering. 2013 37, 929-943.
[10]Aguado, S.; Santolatira, J.; Samper, D.; Aguilar, J.J. Study of self-calibration and multilateration in machine tool volumetric verification for laser tracker error reductions. Part B: Journal of Engineering Manufacture 2013.
[11] Aguado, S.; Samper, D.; Santolaria, J.; Aguilar, J.J. Protocol for machine tool volumetric verification using a commercial laser tracker. The international Journal of Advanced Manufacturing Technology. (2014) DOI 10.1007/s00170-014-6055-5.
[12] Aguado, S.; Samper, D.; Santolaria, J.; Aguilar, J.J. Volumetric Verification of Multiaxis Machine Tool Using Laser Tracker. The Scientific World Journal (2014). ID 959510, 16 page.


