Predicción de la capa templada en el 'grind-hardening' de piezas cilíndricas mediante un modelo FEM 3D
El rectificado cilíndrico es un proceso de mecanizado de elevada precisión ampliamente empleado en piezas de revolución (en torno a un 75% de las piezas rectificadas utilizan esta aplicación). Muchas de las piezas rectificadas son endurecidas superficialmente mediante procesos que son difíciles de integrar en las líneas de producción. El 'grind-hardening' es un proceso novedoso que pretende llevar a cabo el endurecimiento y acabado de la pieza mediante un único proceso de mecanizado. Con el objetivo de estudiar la generación excesiva de calor y su repercusión sobre las piezas rectificadas, en anteriores trabajos se desarrolló un modelo térmico de elementos finitos 3D para rectificado cilíndrico en traverse. En este trabajo se evaluará la validez del modelo para predecir la capa templada en pruebas experimentales de grind-hardening en piezas de acero AISI 1045. Además, se ha evaluado la posibilidad de utilizar el método de ruido Barkhausen como ensayo no destructivo para predicción de la capa templada en la pieza.
1. Introducción
El rectificado cilíndrico en traverse es un proceso industrialmente utilizado para el acabado de superficies de revolución. En etapas anteriores del proceso de fabricación, muchos componentes mecánicos han sido endurecidos superficialmente mediante tratamientos térmicos como el temple por inducción. Sin embargo, este tipo de procesos son muy difíciles de integrar en las líneas de producción y, además, presentan un coste elevado. Ante esto, en las últimas décadas, se han desarrollado procesos innovadores como el ‘grind-hardening’ que pretenden llevar a cabo el endurecimiento y el acabado de la pieza mediante un único proceso de mecanizado [1, 2, 3]. Este proceso aprovecha el calor generado en la interacción de los granos de abrasivo con la pieza para elevar la temperatura por encima de la de austenización en un periodo de tiempo muy corto. Debido, por un lado, a los exigentes requisitos de acabado, integridad superficial y tolerancias dimensionales y, por otro lado, al elevado número de variables que influyen en el proceso, la selección de los parámetros de mecanizado para la puesta a punto de este proceso requiere de un elevado número de ensayos experimentales. Por ello, se han desarrollado modelos matemáticos para 'grind-hardening' en rectificado plano [4, 5, 6] y para 'grind-hardening' en rectificado cilíndrico [7,8] que pretenden reducir esa fuerte componente experimental.
Un aspecto importante a tener en cuenta es el estado tensional de la pieza tras el proceso de acabado. La deformación plástica no homogénea (debido a las elevadas variaciones de temperatura y esfuerzos mecánicos en la superficie) y los cambios de volumen generados por cambios en la micro-estructura del material, pueden provocar tensiones residuales indeseadas que afecten a la vida a fatiga de la pieza.
Sin embargo, la detección de este tipo de estados tensionales requiere de técnicas destructivas o semi-destructivas como 'hole-drilling', la eliminación de capas o la difracción de rayos X. En las últimas décadas se ha hecho un importante esfuerzo por desarrollar técnicas no destructivas como, por ejemplo, la basada en el ruido de Barkhasuen, que permitan predecir el estado tensiona de la pieza, así como los cambios en la estructura metalúrgica que haya podido sufrir el material durante el mecanizado.
La señal de ruido Barkhausense atribuye al movimiento irreversible de los domuinios magnéticos durante un proceso de magnetización cíclica. Este movimiento está fuertemente influenciado por la microestructura del material y por el estado tensional de la pieza [10]. Hasta el momento, este método únicamente permite compara dos estados de lapieza de firma cualitativa. Sin embargo, recientes trabajos han intentado prededir de forma cuantitativa la distribución de tensiones residuales [11, 12, 13] o la evolución de la dureza del material bajo la superficie [14, 15].
El objetivo de este trabajo es desarrollar un modelo FM 3D para rectificado cilíndrico en traverse que permita prefecir la profundidad de capa templada en el proceso de grind-hardening. Asimismo, se evaluará la posibilidad de utilizar el método de ruido Barkhausen como ensayo no destructivo para predicción de la profundidad de la capa templada generada en la pieza.
2. Descripción del modelo FM
La simulación mediante elementos finitos del proceso de grind-hardening tiene como objetivo la preducción del espesor de la capa templada. Los modelos térmicos de rectificado sustituyen la acción de la muela sobre la pieza por una fuente de calor que se mueve sobre ésta con un movimiento igual al relativo entre la muela y la pieza. Para ello, resulta imprescibndible definir correctamente la zona de contacto sobre la que se aplica la fuente, la distribuciónd el calor sobre ésta as como la cantidad del calor total generado que se evacúa a través de la pieza.
2.1. Estimación de la zona de contacto
Tal y como se observa en la figura 1, la zona de contacto se ha considerado como una superficie cilíndrica. En los ensayos experimentales, que se comentarán posteriormente, se observó que el desgaste de la muela era irregular. Al existir un tipo de contacto diferente (ver figura 4) en cada zona de la muela, sería necesario definir varias fuente s de calor. Esto complicaría excesivamente el modelo y, por ello, se ha optado considerar una única fuente de calor sobre una anchura de muela efectiva (bseff).
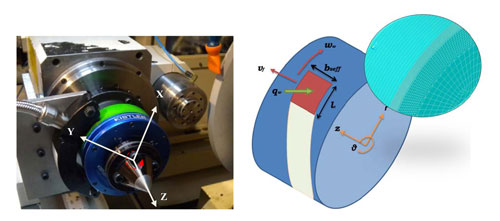
En cuanto a la longitud de la zona de contacto (lc) se ha considerado que ésta puede aproximarse a partir de la expresión proporcionada por Rowe et. al. [15]:
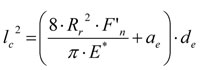
Donde:
• F’n: fuerza específica de rectificado que puede obtenerse a partir de la siguiente expresión:
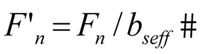
Donde Fn es la fuerza normal en la zona de contacto entre la muela y la pieza y bseff el ancho muela efectivo comprometido en el corte. El valor de la fuerza normal ha sido medido mediante un dinamómetro rotativo Kistler 9123C colocado en el cabezal pieza. Este dinamómetro es capaz de medir tres fuerzas (Fx, Fy, y Fz) en las direcciones de los ejes de un sistema de coordenadas móvil (ver figura 1).
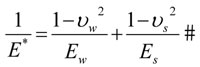
- E*: representa las propiedades elásticas de la muela y la pieza.
Teniendo en cuenta los siguientes valores aproximados de las propiedades elásticas del acero y de la muela:
o Módulo de elasticidad del acero: 210 GPa.
o Módulo de elasticidad de la muela: 50 GPa.
o Coeficiente de Poisson del acero: 0,29.
o Coeficiente de Poisson de la muela: 0,22.
Se obtiene un valor de dicho coeficiente de 42,75 GPa.
- Rr: factor de rugosidad. Según Rowe [15] un valor de Rr=5 proporciona valores de longitud de contacto adecuados cuando la muela se encuentra embotada (ver apartado 3.1).
- ae: profundidad de pasada radial real.
- de: diámetro equivalente. Su valor puede obtenerse a partir del diámetro de la muela (ds) y de la pieza (dw) a partir de la siguiente expresión:
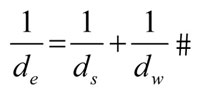
2.2. Cantidad de calor evacuada hacia la pieza y distribución de calor
La energía consumida durante el proceso de rectificado en se transforma, prácticamente en su totalidad, en calor en la zona de contacto entre la muela y la pieza. Su valor puede aproximarse a partir de la siguiente expresión:
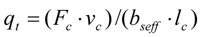
Donde Fc es la fuerza de corte, vc es la velocidad periférica de la muela, bseff es el ancho de la muela efectivo comprometido en el corte y lc es la longitud de contacto real. Esta energía calorífica es evacuada a través de la pieza, la muela, la viruta y el fluido refrigerante. La fracción de calor evacuada hacia la pieza puede obtenerse a través del parámetro Rw (fracción de la energía total que se deriva hacia la pieza).
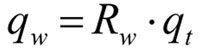
3. Validación del modelo mediante ensayos experimentales
3.1. Ensayos planteados
Los ensayos fueron realizados en una rectificadora cilíndrica de exteriores Danobat FG-600-S utilizando una muela de alúmina blanca Tyrolit CS33A802HH4VK1 de diámetro 400 mm y anchura 18,5 mm. En cuanto al material utilizado en las probetas de los ensayos, se eligió un acero medio en carbono (AISI 1045), y éstas fueron cilindradas y posteriormente rectificadas hasta un diámetro exterior de 50 mm. Por otro lado, durante los ensayos se tomaron medidas de la potencia consumida por el cabezal muela y de las fuerzas generadas durante el proceso.

Se llevaron a cabo tres ensayos en los que se realizó una pasada en seco con los parámetros indicados en la tabla 1. Antes de cada uno de los ensayos, la muela fue diamantada con una loseta de diamante multipunta, utilizando para ello una velocidad de muela de 35 m/s, una velocidad de avance de 200 mm/min y una profundidad de pasada radial de 10 μm. Durante los ensayos, no se utilizó ningún tipo de refrigerante, ya que se ha pretendido favorecer el aumento de la temperatura del material por encima de la de cambio de fase. Sin embargo, el calentamiento de la muela podría acelerar su desgaste. Danobat propone (mediante un sistema patentado con referencia ES2315064B1) refrigerar la muela en un punto alejado de la zona de contacto evitando así el enfriamiento de la pieza.

En las figuras 4 y 5 se observa el aspecto de la pieza y el estado de la muela tras la pasada de rectificado en seco para los ensayos 1 y 2 respectivamente.


El aspecto de las muelas después de cada uno de los ensayos indica que el desgaste producido a lo largo del ancho de la muela no ha sido uniforme. En la figura 4, se observa que aproximadamente un tercio de la muela se encuentra embotada. En esta zona, la fricción entre la muela y la pieza será más fuerte y se generarán elevadas cantidades de calor (durante el ensayo se observó que en esta zona se concentraba la viruta incandescente). A continuación, se presenta otra zona gris (característica del proceso de rectificado) y por último una zona blanca que apenas ha mecanizado material.
En el ensayo 2, sin embargo, la zona embotada se encuentra en el centro de la muela. En este caso, durante el ensayo, se observó aproximadamente en la zona central de la pieza la viruta incandescente se desplazaba hacia el centro de la muela. Este efecto puede deberse a que un aumento excesivo de las fuerza normal en el primer segmento (provocando por un embotamiento excesivo de la muela) haya provocado la rotura de los puentes de aglomerante, generando, por lo tanto, un desgaste severo de la muela. Por esta razón, se ha decido considerar la hipótesis de que, en cada instante del ensayo, la anchura de muela comprometida en el corte (bseff) es 2/3 de la anchura total de ésta. Esta hipótesis intenta simplificar el hecho de emplear tres fuentes independientes en el modelo al suponer una única fuente con un ancho activo de 2/3 del ancho de la muela y que sea representativa de lo que sucede en toda ella.
3.2. Validación del modelo FEM
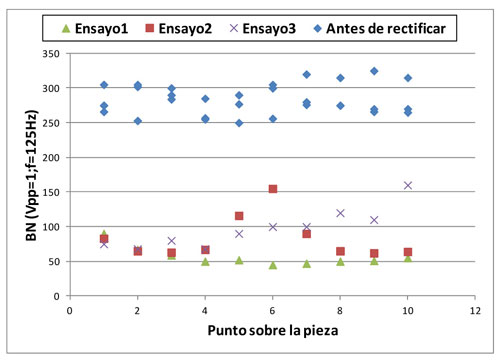
La validación del modelo de elementos finitos se ha realizando comparando la capa templada en cada probeta con la profundidad del modelo a la cual se alcanza la temperatura de cambio de fase. Con el objetivo de obtener información a cerca de la existencia de dicha capa templada mediante un ensayo no destructivo, se ha se han medido valores de ruido Barkhausen utilizando un equipo Rollscan 300 de Stresstech Group. En la figura 6 se observan los valores de BN antes y después de los tres ensayos en 10 puntos de la pieza espaciados 20 mm. Tal y como se ha comentado anteriormente, aunque existen trabajos en los que se intenta relacionar los valores absolutos de nivel de ruido Barkhausen con la microestructura y el estado tensional del material, actualmente, estas medidas aportan únicamente información cualitativa. Por lo tanto, es necesario tomar medidas de BN de la pieza sin capa templada antes de rectificar como valor de referencia a comparar.
Tal y como se observa en la figura 6, el nivel de ruido Barkhausen no es uniforme a lo largo de la probeta. Este efecto se debe a que el desgaste irregular de la muela ha provocado que el rozamiento generado en la intercara muela-pieza (y por lo tanto la cantidad de calor generada en el proceso y la profundidad de capa templada) varíe a lo largo de la longitud de la pieza rectificada.
A continuación se ha estudiado la profundidad de capa templada en las probetas en la izquierda, centro y derecha de éstas. En la figura 7 se muestran tres micrografías donde se observa la profundidad de capa templada en cada uno de los tres ensayios en el extremo derecho de la pieza. Las profundidades obtenidas son de 140 µm para el ensayo 1, 80 µm para el ensayo 2 y 36 µm para el ensayo 3 respectivamente.

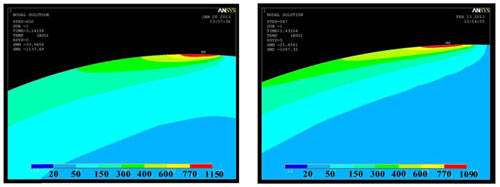
Partiendo de la hipótesis de que el ancho de muela comprometido en el corte se corresponde con 2/3 de la anchura total de la muela, se han llevado a cabo varias simulaciones para cada uno de los tres ensayos. El modelo representa una correlación excelente con la realidad para valores del parámetro Rw de 0,65 (ensayo 1), 0,675 (ensayo 2) y 0,8 (ensayo 3). Estos valores de la fracción de energía evacuada hacia la pieza están de acuerdo con los obtenidos por autores para rectificado con muelas de alúmina [16, 17, 18, 19].
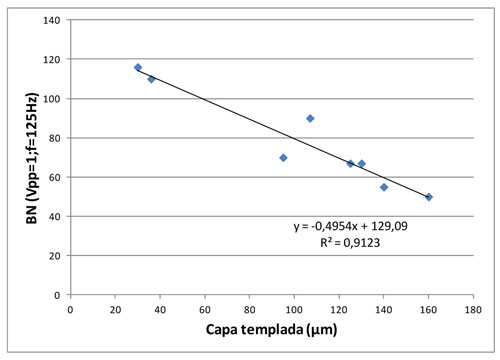
Por otro lado, en la figura 8 se muestran los valores de ruido Barkhausen correspondientes a cada una de las profundidades de capa templada. Se observa que la relación es aproximadamente lineal, por lo tanto, este método puede ser utilizado para obtener una estimación de la profundidad de capa templada en el material. Sin embargo, ha de tenerse en cuenta que el estado tensional de la pieza también afecta también al nivel de ruido Barkhausen registrado, por lo que sería conveniente llevar a cabo un estudio de las distribución de las tensiones residuales en la pieza.
Un parámetro importante a tener en cuenta en la toma de medidas de BN es la profundidad asociada a ésta (en la práctica la profundidad de la medida suele variar entre 0,01 y 2 mm). El espectro de potencia de la señal de ruido Barkhausen emitida a una determinada profundidad se ve amortiguado por el material que se encuentra sobre éste. Los principales factores que determinan la intensidad del amortiguamiento son la conductividad eléctrica y la permeabilidad magnética del material. La profundidad asociada a la señal para un ancho de banda determinado puede estimarse a partir de la expresión 7.
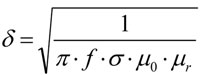
Donde ƒ es la frecuencia de la señal de ruido BN, σ la conductividad eléctrica del material, μr la permeabilidad magnética relativa del material y μ0 la permeabilidad magnética del vacío.
Los valores de BN proporcionados por el equipo y mostrados en las figuras 6 y 8 corresponden al valor eficaz de la señal (valor cuadrático medio o RMS) para el ancho de banda de 70-200 kHz. Teniendo en cuenta que la conductividad de la martensita para el acero AISI 1045 es aproximadamente 0,41•107Ω-1m-1 y la permeabilidad relativa 75 [20], la profundidad máxima asociada a la señal analizada corresponde a 110 μm. Esta profundidad es adecuada para comparar capas templadas con profundidad inferior o próxima a este valor. Por lo tanto, se debe adecuar este valor a la profundidad de capa estimada, ya que en caso contrario no es posible su predicción mediante ruido BN.
4. Conclusiones
En este trabajo se ha presentado un modelo que permite predecir la profundidad de capa templada en el proceso de grind-hardnening. El análisis del estado de la muela tras el rectificado sugiere que los mecanismos de arranque son distintos en cada zona de ésta. Ante la dificultad de introducir varias fuentes de calor en cada zona de la muela en el modelo, se ha considerado una anchura de muela comprometida en el corte efectiva (bseff) sobre la que se ha dispuesto una única fuente de calor. Para los ensayos realizados, la consideración de un ancho de muela efectivo de 2/3 del ancho de muela total junto con el ajuste de la fracción de calor evacuada hacia la pieza permite predecir correctamente la profundidad de capa templada.
Por otro lado, se ha observado que existe una correlación entre el valor cuadrático medio (RMS) de la señal de ruido Barkhausen y la profundidad de capa templada en la pieza.
Por lo tanto, podría utilizarse este método como un ensayo no destructivo para predicción aproximada de la capa templada en la pieza.
5. Agradecimientos
Se agradece la contribución del Ministerio de Ciencia e Innovación (MICINN) por la subvención del Proyecto de Investigación ‘Integración de modelos numéricos y técnicas experimentales para el aumento del valor añadido en el rectificado de componentes de precisión’ de código DPI-2010-21652-C02-00.
Bibliografía
[1] Brinksmeier E, Brockhoff T. Randschicht-Wärmebehandlung durch Schleifen. HTM J. Heat Treatm. Mat., Vol. 49, No. 5, 1994, pag. 327-330.
[2] E. Brinksmeier and T. Brockhoff, ‘Utilization of Grinding Heat as a New Heat Treatment Process’, CIRP Annals - Manufacturing Technology, vol. 45, no. 1, pag. 283-286, 1996.
[3] E. Brinksmeier and T. Brockhoff, ‘Advanced grinding processes for surface strengthening of structural parts’, Machining Science and Technology, vol. 1, no. 2, pag. 299- 309, 1997.
[4] M. F. Zäh, E. Brinksmeier, C. Heinzel, J.-W. Huntemann, and T. Föckerer, ‘Experimental and numerical identification of process parameters of grind-hardening and resulting part distortions’, Production Engineering, vol. 3, no. 3, pag. 271-279, 2009.
[5] T. Nguyen and L. C. Zhang, ‘Grinding–hardening using dry air and liquid nitrogen: Prediction and verification of temperature fields and hardened layer thickness’, International Journal of Machine Tools and Manufacture, vol. 50, no. 10, pag. 901-910, 2010.
[6] T. Foeckerer, M. F. Zaeh, and O. B. Zhang, ‘A three-dimensional analytical model to predict the thermo-metallurgical effects within the surface layer during grinding and grindhardening’, International Journal of Heat and Mass Transfer, vol. 56, pag. 223-237, 2013.
[7] V. S. K. Venkatachalapathy and B. Rajmohan, ‘Experimental Studies on the Grind-Hardening Effect in Cylindrical Grinding’, Materials and Manufacturing Processes, vol. 18, no. 2, pag. 245-259, 2003. 9
[8] T. Nguyen and L. C. Zhang, ‘Realisation of grinding-hardening in workpieces of curved surfaces—Part 1: Plunge cylindrical grinding’, International Journal of Machine Tools and Manufacture, pag. 1-11, 2010.
[9] G. Totten, M. Howes y T. Inoue. Handbook of Residual Stress and Deformation of Steel. 1ª ed. ASM International, 2002.
[10] D. Jiles, ‘Review of magnetic methods for nondestructive evaluation’, NDT & E International, vol. 21, no. 5, pag. 311-319, 1988.
[11] O. Kypris, I. C. Nlebedim, and D. C. Jiles, ‘Mapping Stress as a Function of Depth at the Surface of Steel Structures Using a Frequency Dependent Magnetic Barkhausen Noise Technique’, IEEE Transactions on Magnetics, vol. 48, no. 11, pag. 4428-4431, 2012.
[12] N. S. Prabhu, J. Joseyphus, T. S. N. Sankaranarayanan, B. R. Kumar, a. Mitra, and a. K. Panda, ‘Residual Stress Analysis in Surface Mechanical Attrition Treated (SMAT) Iron and Steel Component Materials by Magnetic Barkhausen Emission Technique’, IEEE Transactions on Magnetics, vol. 48, no. 12, pag. 4713-4717, 2012.
[13] L. Mierczak, D. C. Jiles, and G. Fantoni, ‘A New Method for Evaluation of Mechanical Stress Using the Reciprocal Amplitude of Magnetic Barkhausen Noise’, IEEE Transactions on Magnetics, vol. 47, no. 2, pag. 459-465, 2011.
[14] P. Zerovnik, J. Grum, and G. Zerovnik, ‘Determination of Hardness and Residual- Stress Variations in Hardened Surface Layers With Magnetic Barkhausen Noise’, IEEE Transactions on Magnetics, vol. 46, no. 3, pag. 899-904, 2010.
[15] W.B. Rowe, M.N. Morgan, H. S. Qi, H. W. Zheng. ‘The effect of deformation on the contact area in grinding’. Annals of the CIRP, 42, pag. 409–412,1993.
[16] AM. O. Mohamed, A. Warketin, R. Bauer. ‘Use of surface roughness measurements to improve the estimation of the heat partition in grinding’. Journal of Materials Processing Technology, 211, pag. 566-572, 2011.
[17] Z. B. Hou, R Komanduri. ‘On the mechanics of the grinding process, PartII-Thermal analysis of fine grinding’. Int. Journal of Machine Tools & Manufacture, vol. 44, pag. 247- 270, 2004.
[18] W. Brian Rowe. ‘Thermal analysis of high efficiency deep grinding’. Int. Journal of Machine Tools and Manufacture, vol. 4, 1/1-19, 2001.
[19] S. Malkin and C. Guo, ‘Thermal Analysis of Grinding’, Annals of the CIRP, vol. 56, no. 2, pag. 760-782, 2007.
[20] S. Kahrobaee and M. Kashefi, ‘Hardness profile plotting using multi-frequency multioutput electromagnetic sensor’, NDT & E International, vol. 44, no. 4, pag. 335-338, Jul.












