Análisis de la capacidad de medición de una MH evaluando su incertidumbre con el método Monte Carlo
El aumento de la precisión dimensional requerida, las tolerancias geométricas y otras tareas, especialmente en el sector del mecanizado de piezas de gran valor añadido, ha ido desplazando a los instrumentos de medición tradicionales de las tareas de calibración. Las principales limitaciones que presentan estos son la precisión de los sistemas, el rango de trabajo y el tiempo necesario. La calibración de máquina herramienta (MH) se define como el proceso a partir del cual determinar la influencia de los errores geométricos de la máquina, con objeto de corregir el comportamiento sistemático de estos mediante una posterior compensación.
Los errores geométricos de la MH son la diferencia entre la respuesta real de una máquina a un comando emitido de acuerdo con el protocolo aceptado del funcionamiento de esa máquina y la respuesta a ese comando anticipado por ese protocolo [1]. Actualmente existen dos técnicas de identificación de los errores geométricos de MH. Medición directa [2, 3], que trata de medir cada uno de los errores geométricos de los ejes de movimiento individualmente, y medición indirecta [2], basada en la medición del efecto conjunto de todos ellos.
Los resultados proporcionados por el proceso de calibración llevan asociados una incertidumbre que caracteriza la dispersión de los resultados obtenidos en función de las diferentes fuentes de error que afectan al proceso. La organización internacional para la estandarización (ISO) ha desarrollado y publicado diferentes guías para la representación de la incertidumbre de medición (GUM), como la norma UNE-ISO/TR 230-9 [4] encargada de la estimación de la incertidumbre de medida para los ensayos de máquina-herramienta, o ISO/TS 14253-2 [5]. Esta combina la estimación de las distintas fuentes de error y sus incertidumbres típicas asociadas para determinar la incertidumbre típica asociada al proceso global. En procesos tan complejos como la calibración de MH mediante VV las limitaciones de la GUM hacen recomendable la utilización del Método de Montecarlo [6]. De las distintas fuentes de incertidumbre, este artículo se centra en la influencia del error que genera el ruido del sistema de medida (láser tracker), al considerarse este un parámetro con gran influencia en la incertidumbre global del proceso que, sin embargo, no suele tenerse en consideración.
Principios de la verificación volumétrica
La verificación volumétrica consiste en un proceso intensivo de identificación de parámetros del modelo cinemático de la MH a partir de una función objetivo. Esta se basa en la minimización de la diferencia entre pares de puntos teóricos y reales a través del modelo cinemático de la máquina. La diferencia entre puntos reales y puntos teóricos mostrará la influencia conjunta de los errores para cada punto, a partir de los cuales obtener el error volumétrico cuadrático medio de la máquina (Ev) [7].
A diferencia de un interferómetro láser, el láser tracker proporciona información de la influencia conjunta de todos los errores geométricos. Por lo tanto, la diferencia entre las series de puntos nominales y medidos, tal como se define en la ecuación 1, puede ser utilizada como error volumétrico para obtener las funciones de aproximación de los errores geométricos de la MH.

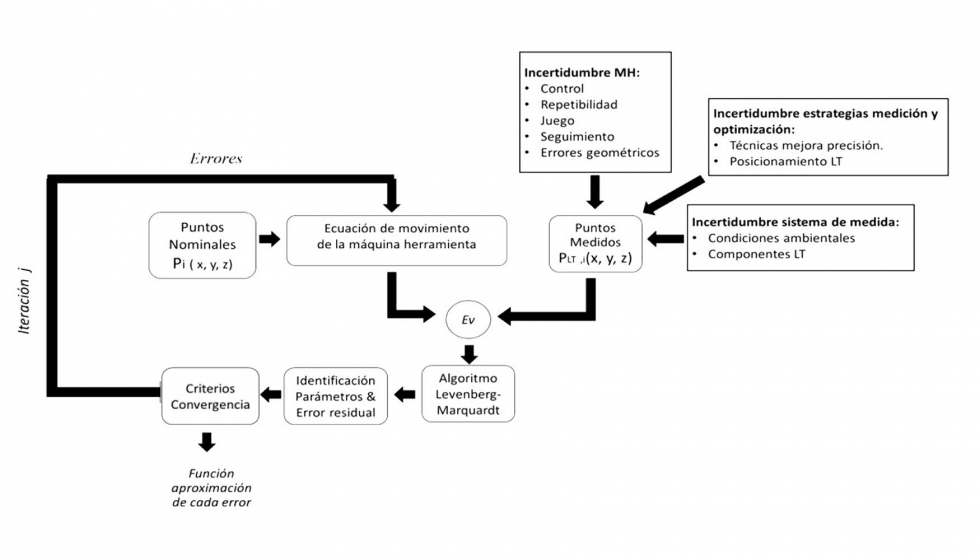
En el Ev está incorporada, además de la influencia de los errores geométricos, la influencia de otras fuentes de incertidumbre como el ruido de medición, variaciones atmosféricas, errores no geométricos, etc. En la figura 1 se presenta un esquema tanto del proceso de identificación de parámetros, con el que se obtienen las diferentes funciones de regresión con las que se aproximan los geométricos de la máquina, como las distintas fuentes de incertidumbre que afectan a la precisión de los puntos capturados.
Metodología
La norma ISO / TS 15530-3: 2011 [8] proporciona una técnica experimental para la evaluación de la incertidumbre de las mediciones con MMC. La norma mencionada describe el procedimiento de evaluación de incertidumbre tanto para la parte experimental como para el cálculo. La incertidumbre expandida se calcula como:
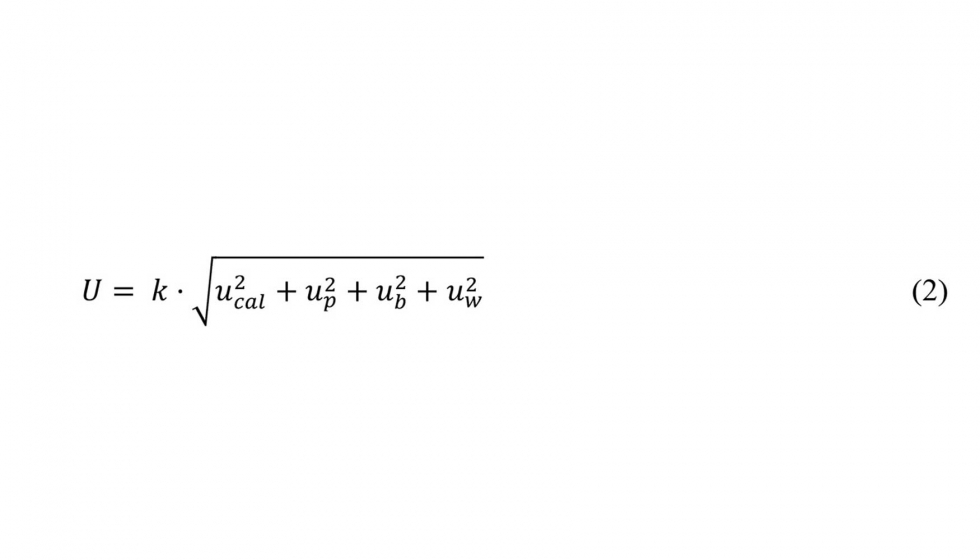
Donde 𝑢𝑐𝑎𝑙 es la incertidumbre estándar asociada con la incertidumbre de calibración de la pieza, 𝑢𝑝 es la incertidumbre estándar resultante del procedimiento de medición del objeto de referencia, 𝑢𝑏 es la incertidumbre estándar asociada con el error sistemático 𝑏, 𝑢𝑤 es la incertidumbre estándar resultante de variaciones del material y (Debido a variaciones del coeficiente de expansión, errores de forma, rugosidad y elasticidad) y 𝑘=2 representa un factor de cobertura del 95%.
El primer término, 𝑢𝑐𝑎𝑙, viene dado en el certificado de calibración de la pieza. También se podría estimar con el error máximo permisible del CMM utilizado en la calibración de la placa y la incertidumbre derivada de la expansión del artefacto de referencia debido a desviaciones térmicas:
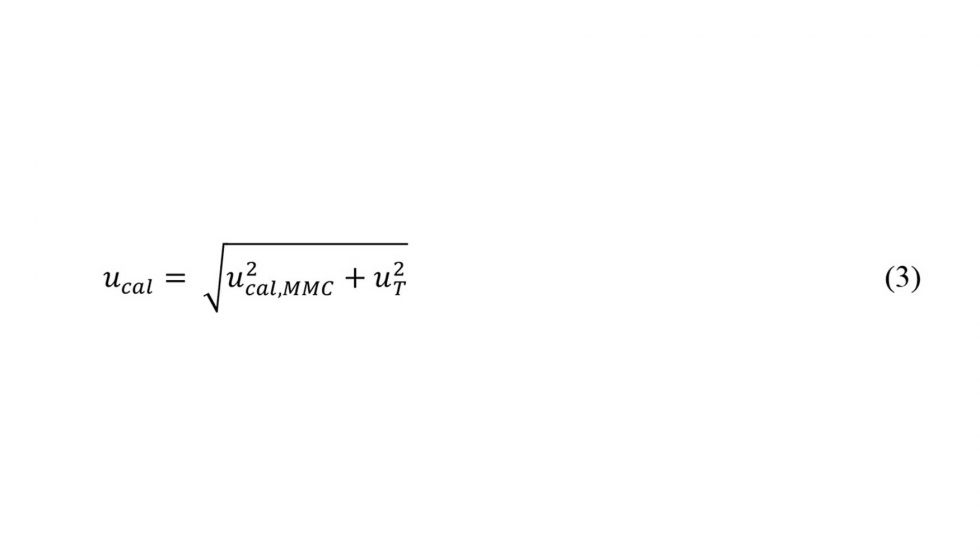
El valor de 𝑢𝑝 se puede calcular en cada posición del espacio de trabajo como dos veces la desviación estándar de la malla simulada de puntos en esa posición. En nuestro caso, este valor se calculará en la sección siguiente: resultados.
De acuerdo con la Guía para la expresión de incertidumbre en la medición (GUM) [9], 𝑢𝑏 se calcula como una incertidumbre de tipo A, por lo tanto:

Donde σ es la desviación estándar del error sistemático b y n es el número de valores simulados. El valor de 𝑢𝑏 podría ser despreciado ya que σ tiene un valor pequeño y n = 1.000.
El valor de 𝑢𝑤 debe ser estimado. Para reducir este término, la expansión térmica ha sido compensada. De este modo, la incertidumbre 𝑢𝑤 está directamente relacionada con la precisión del sensor que mide la temperatura de la placa de agujeros:

Resultados
La ecuación de movimiento que define el modelo cinemático de la máquina, viene determinada por la ecuación 5. Donde el vector 𝑋𝐿𝑇 representa las coordenadas de un punto nominal P (x, y, z) medido con el LT, en función de la posición del LT y errores geométricos de la máquina [7].
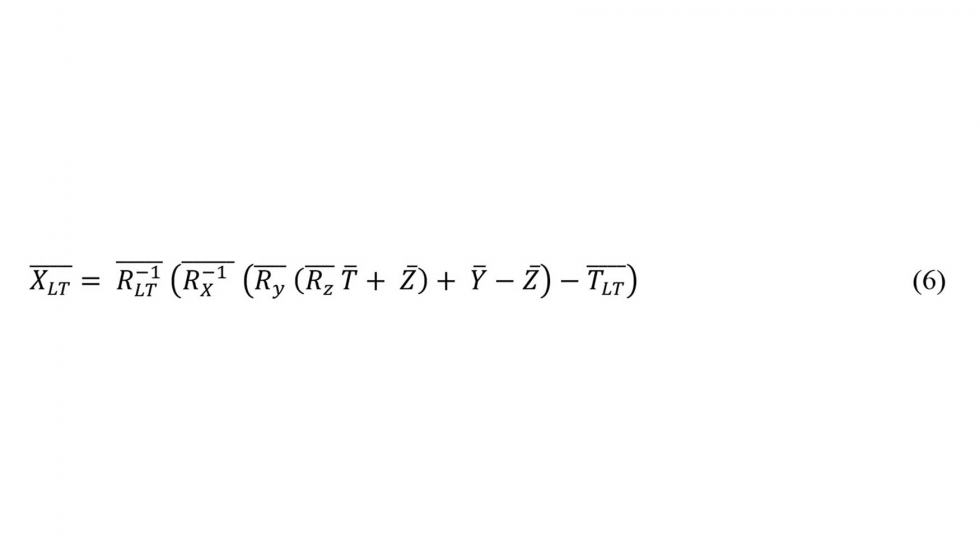
Los algoritmos implementados permiten, a partir del modelo cinemático de la máquina, tener en consideración el proceso de verificación completo junto con las diferentes fuentes de incertidumbre que afectan al mismo. Los diferentes algoritmos que forman el software desarrollado, base de la generación de ensayos a ser analizados por el método de Monte Carlo son:
A. Características de la máquina. Dimensiones del volumen de trabajo, secuencia de movimientos, errores geométricos, etc.
B. Localización del sistema de media respecto al volumen de la máquina a verificar. Algoritmo encargado en función de las características del ruido de medida y el volumen a verificar de encontrar la posición óptima.
C. Técnicas y estrategias utilizadas para la identificación de los errores geométricos. Diferentes polinomios a utilizar, grado, criterios y secuencia de identificación, etc.
D. Factores de incertidumbre considerados en el estudio. Elección de los parámetros que se desean analizar.
E. Generación de ensayos en función de los factores de incertidumbre a analizar, funciones de distribución que los modelan y características de definidas en los puntos anteriores.
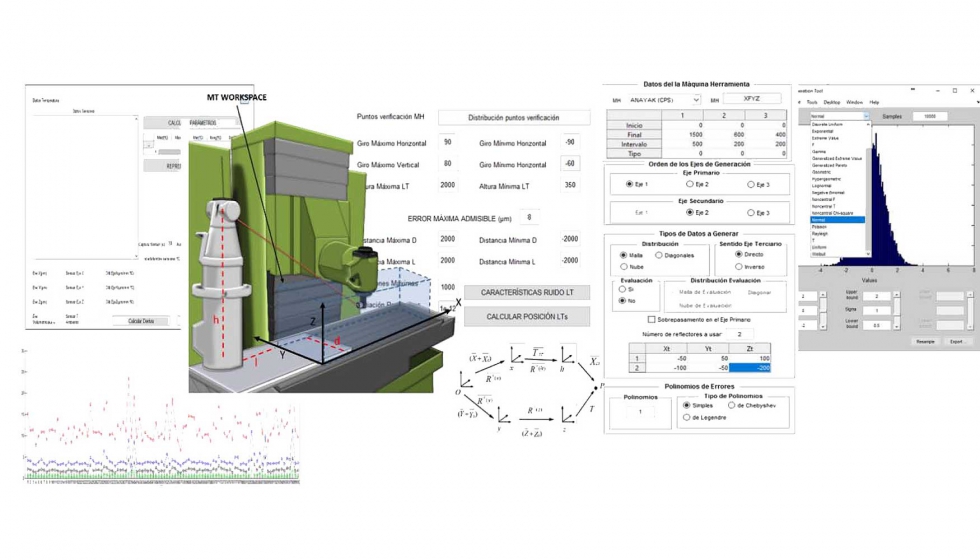
Utilizando el software desarrollado se introduce la incertidumbre de medida consecuencia de los componentes (interferómetro y encoders angulares) del láser tracker. Estos se modelan mediante una distribución normal de 24 μrad para los encóderes angulares y 4 +/- 0,8 μm/m para el error radial. Esta influencia afecta al error volumétrico y por lo tanto a las funciones de aproximación obtenidas en función de: distribución espacial del láser tracker respecto a sistema de coordenadas de la máquina, y la incertidumbre que se introduce en cada punto medido.
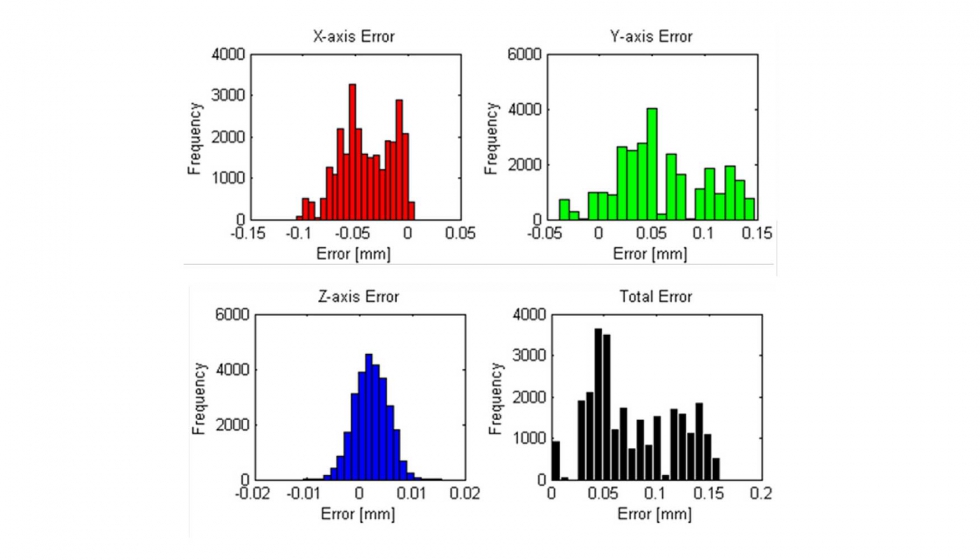
El valor de cada uno de los errores se introduce en las ecuaciones anteriores a través de una serie de funciones de generación. Se realiza una optimización del mismo modo que se realizaría al llevar a cabo una verificación volumétrica, quedando la siguiente distribución de error volumétrico residual:
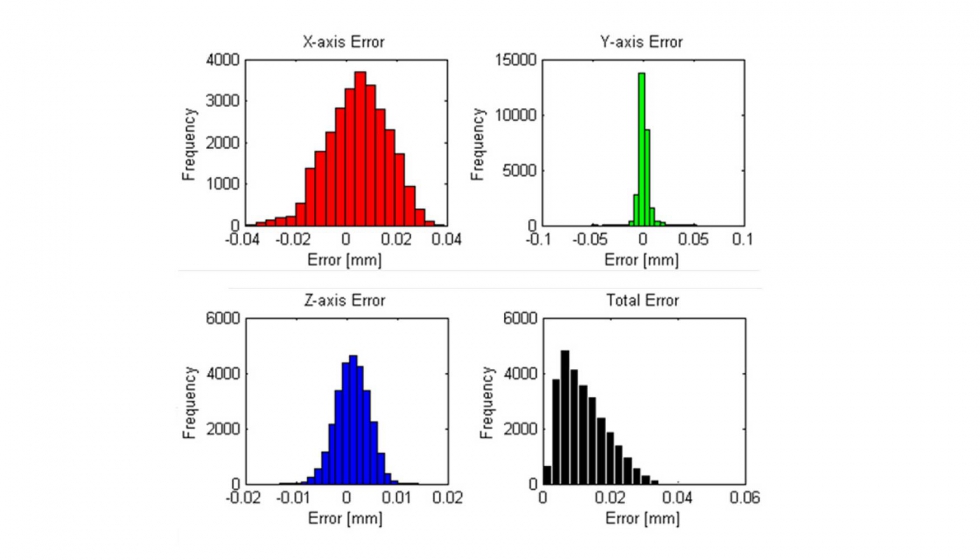
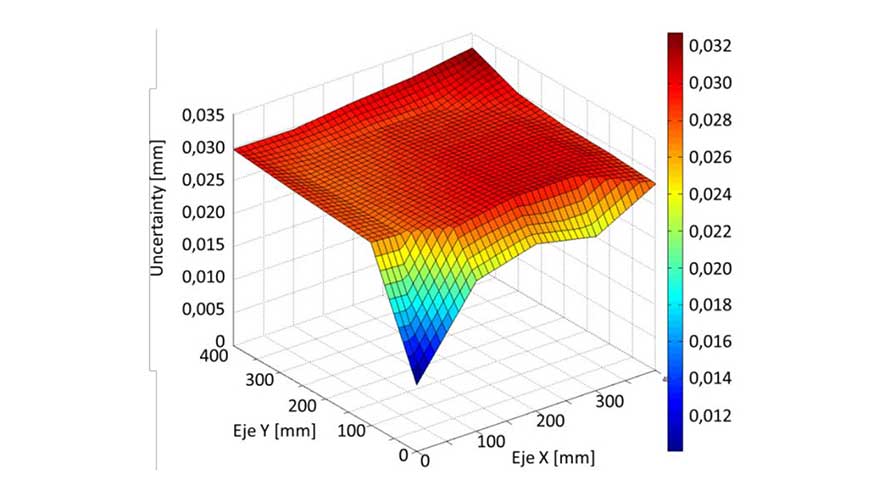
Al estar cada uno de los puntos de cada uno de los ensayos afectado por diferente valor del ruido de medida del LT, se observa como esta influencia en los errores en cada una de las coordenadas tiene una distribución normal, tres primeras gráficas de la figura 4. Si observamos el valor en distancia, notar que al calcular el error en distancias y en función de la ecuación 1, no tenemos errores negativos ya que estos se están tomando en modulo, véase la última gráfica de la figura 4. Al tener en cuenta estas consideraciones, el error residual medio en distancia tiene una distribución de probabilidad con forma de normal sesgada de 12,34 μm de valor medio y 7.06 μm de desviación típica. El valor de esta desviación típica para cada punto del espacio de trabajo es usado como incertidumbre del proceso, 𝑢𝑝, mencionada en la ecuación 2. El valor de 𝑢𝑏 se calcula con la ecuación 4, dándole los valores de 𝜎=7.06 μ𝑚 y 𝑛=1000, dando como resultado 𝑢𝑏=0.223 μ𝑚. De este modo, la incertidumbre expandida resultante puede verse en la figura 5.
Conclusiones
La determinación de la incertidumbre de calibración de MH mediante técnicas de verificación volumétrica mediante LT no puede obtenerse mediante la ley de propagación de errores (GUM). Para ello es necesaria la aplicación del método de Montecarlo.
El método de Montecarlo se beneficia de la gran capacidad computacional de los ordenadores actuales para generar números aleatorios dentro de diferentes funciones de distribución de error. A la influencia de los errores geométricos de los ejes de movimiento de la máquina, obtenida a partir de su modelo cinemático, el software desarrollado permite introducir la influencia de los factores de influencia de la máquina, equipo de medida utilizado, y la incertidumbre de las estrategias de medición y optimización. La determinación de la incertidumbre del proceso de calibración resulta esencial a la hora de conocer la capacidad real de nuestra máquina. Los ensayos presentados se centran en la influencia de la incertidumbre de medición de un LT, punto inicial del proceso de verificación, al considerarse este uno de los parámetros más influyentes.
Agradecimientos
Este trabajo ha sido financiado por el Gobierno Español (Ministerio de Economía y Competitividad) a través del proyecto de investigación METRAP - Desarrollo de nuevas técnicas de verificación y compensación de los sistemas de fabricación y trazabilidad en proceso (DPI2013-46979-C2-1-P), dentro del Programa Estatal de Fomento de la Investigación Científica y Técnica de Excelencia, y por el Gobierno de Aragon (Departamento de Industria e Innovación) a partir de subvenciones a la actividad investigadora de los grupos de investigación reconocidos por el Gobierno de Aragon (2014-T62 Grupo de Ingeniería de Fabricación y Metrología Avanzada).
Bibliografía
[1] ASME B5.54-2005 Methods for Performance Evaluation of Computer Numerically Controlled Machining Centers.
[2] Schwenke, W.Knapp, H.Haitjema, A.Weckenmann, R.Schmitt, F.Delbressine. Geometric error measurement and compensation of machines. Manufacturing Technology, 57, (2008) 660-675.
[3] UNE/ISO-230-1:2014 Máquinas-herramienta. Código de verificación de máquinas-herramienta. Parte 1: Precisión geométrica de las máquinas funcionando en vacío o en condiciones cuasi-estáticas.
[4] ISO/TR 230-9:2005 Estimation of measurement uncertainty for machine tool tests according to series ISO 230, basic equations.
[5] ISO 14253-2-2011 Inspection by measurement of workpieces and measuring equipment — Part 2: Guidance for the estimation of uncertainty in GPS measurement, in calibration of measuring equipment and in product verification.
[6] Evaluación de datos de medición. Suplemento 1 de la Guía para la expresión de la incertidumbre de medida. Propagación de incertidumbres utilizando el método de Montecarlo. http://www.cem.es/sites/default/files /suplemento20120de20gum.pdf
[7] S.Aguado, D.Samper, J.Santolaria, J.J.Aguilar.Improving a real milling machine accuracy through an indirect measurement of its geometric errors. Journal of Manufacturing Systems. Vol 40. 2016. p.p. 26-36.
[8] ISO/TR 15530-3:2011 Coordinate measuring machines (CMM): Technique for determining the uncertainty of measurement – Part 3: Use of calibrated workpieces or measurement standards.
[9] Evaluación de datos de medición. Guía para la expresión de la incertidumbre de medida. Edición digital. http://www.cem.es/sites/default/files/gum20digital1202010.pdf.







