Influencia de las solicitaciones estáticas en el comportamiento de una barrera dinámica de protección contra desprendimientos
Roberto Luis Fonseca, Ing. Caminos, Canales y Puertos, PhD. Grupo Geobrugg
Miguel León García, Ing. Caminos, Canales y Puertos. LDH Ingenieros
Ricardo De Stefano Pérez, Ing. Civil, MBA. Grupo Geobrugg
Rolando Romero Rojas, Ing. Politécnico. Grupo Geobrugg
04/05/2021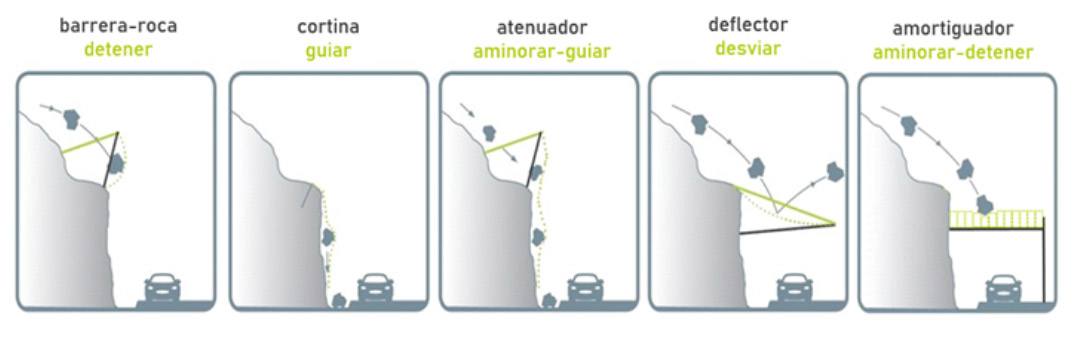
Fig. 1. Sistemas de protección contra desprendimientos rocosos.
La idea de los sistemas flexibles de protección contra desprendimientos rocosos nació en los Alpes suizos como sistematización de la lección aprendida, en los ya existentes sistemas flexibles para el control de la generación de avalanchas producto de la acumulación de nieve en las cornisas. En una primera instancia, solo la experiencia era la herramienta de valoración de las soluciones. Durante muchos años esta tecnología se ha desarrollado, alcanzando el actual límite en 2017 cuando se diseñó, ensayó y posteriormente se instaló la primera barrera que superó el umbral de los 10MJ, una barrera dinámica flexible tipo RXE-10.000 de Geobrugg.
Enfoque energético
Para comprender con facilidad la terminología a la que se hace referencia en este tipo de estudios, es necesario hacer algunos apuntes al respecto, que ayuden a comprender el proceso de balance energético, que se produce durante la detección de un impacto. Con independencia de la rigidez del elemento de interposición (sistema de protección contra desprendimientos), la detención de la roca se produce cuando se alcanza la condición de equilibrio entre la energía que trae la roca y el trabajo que realizan las fuerzas resistentes de reacción de la estructura unido a la deformación o desplazamiento de esta. La energía se transforma en trabajo de las fuerzas de reacción en una distancia.
E = W W = ∫ F. d
donde:
E: energía, J
W: trabajo de las fuerzas de reacción, J
R: fuerza de reacción, N
d: desplazamiento, m
Los elementos dinámicos garantizan mediante el desplazamiento (deflexión) que se alcancen mayores elongaciones con menores fuerzas de reacción y por tanto, mayor absorción de energía. El análisis de la expresión conduce a que para el caso de soluciones rígidas o estáticas, debido al desplazamiento nulo o casi nulo que ofrecen, las fuerzas de reacción o soporte son muy elevadas, mientras que para elementos de intercepción flexibles, se neutraliza la fuerza del impacto de una forma más racional debido al desplazamiento que garantiza dicha estructura, absorbiéndose la misma energía con fuerzas de reacción de menor magnitud.
En la figura 2 se puede observar cómo los sistemas dinámicos garantizan mediante la deformación (desplazamiento del punto de impacto D1) que se consiga igualar el trabajo (absorción de energía A1), que realiza una estructura rígida, cuya deformación es baja (en realidad casi nula D2) y requiere mucha capacidad de reacción (fuerza R2). Bajo ambas curvas el área es igual (A1 = A2), luego ambas soluciones, teóricamente equivalen al mismo nivel de energía.
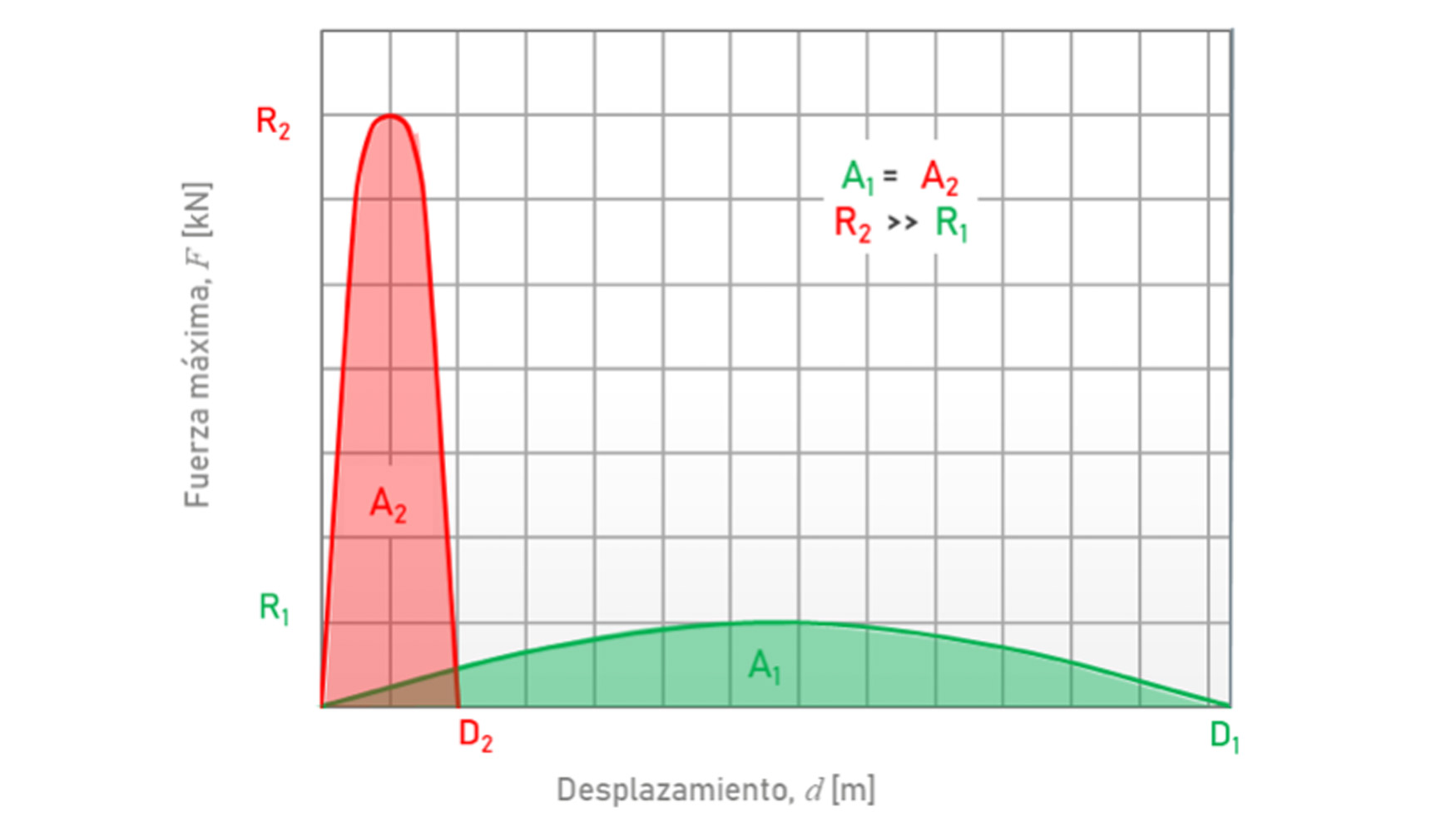
Fig. 2. Balance energético.
Influencia de las solicitaciones estáticas
En una primera instancia la tarea fundamental consistió en resolver técnicamente los valores de solicitaciones dinámicas que se generan sobre todos los elementos del sistema, haciendo que actúen de forma racional, garantizando que las altísimas solicitaciones dinámicas que se producen en un tiempo muy pequeño (< 1 segundo) puedan se transmitidas de forma íntegra a la zona estable del terreno mediante un óptimo sistema de anclajes. Esta ha sido quizá, la tarea más difícil de los especialistas durante años.
Si bien es cierto que estas solicitaciones dinámicas son extremadamente importantes y sin duda son la clave del funcionamiento de los potentes sistemas conseguidos, también es verdad que no se debe dejar a un lado el análisis, las posibles solicitaciones estáticas que se puedan generar básicamente en dos escenarios clave: en primer lugar el impacto de un bloque de grandes dimensiones a una velocidad muy baja, que durante su detención pudiese generar solicitaciones por encima de las consideradas en condiciones estándares y en segundo lugar las cargas que se puedan generar producto del relleno paulatino del trasdós (carga distribuida) de una barrera dinámica (fig. 3).
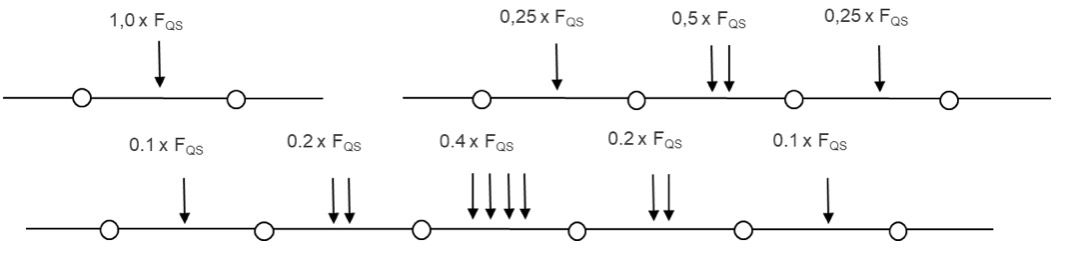
Fig. 3. Diferencia aproximada de la distribución de solicitaciones en el trasdós de la barrera en función del caso de carga.
Esta última combinación es bastante frecuente en instalaciones mineras a cielo abierto, en las que las barreras dinámicas se utilizan con mucho éxito y donde las tareas de limpieza se deben limitar al momento en que las defensas se encuentren completamente llenas (fig. 4).
Este artículo analiza la aplicabilidad y las limitaciones de un enfoque para el diseño de estados límite de barrera flexible, exponiendo el procedimiento de revisión de una barrera dinámica ante el caso especial de carga, en el cual se esperen dichas solicitaciones estáticas.

Fig. 4. Impacto puntual estándar e impacto múltiple que genera acumulación y carga estática. Mandai. Singapur.
A continuación (Tabla 1) se muestra las principales diferencias desde el punto de vista conceptual entre el procedimiento de solución para impactos puntuales donde predomina las cargas dinámicas en comparación con el proceso de llenado paulatino en el que predomina las solicitaciones estáticas.

Determinación de la carga estática
La carga estática del material acumulado se puede calcular utilizando el empuje de tierra activo (Wendeler 2016) tal y como se indica en la siguiente ecuación. La carga estática (peso total de los bloques desprendidos acumulados en el trasdós de la barrera), es en general menor que las altas solicitaciones dinámicas, y muchas veces no relevante (fig. 5).
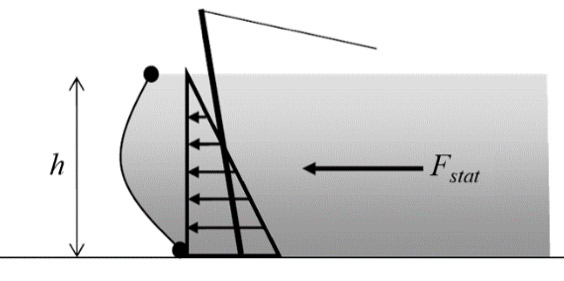
Fig. 5. Fuerza estática en el trasdós de la barrera.
Fstat = ½. γ. h2. Ka. b
donde:
Fstat: carga estática en el trasdós de la barrera, [kN]
γ: densidad del material acumulado, [kN/m3]
h: espesor del material acumulado (altura), [m]
b: longitud sobre la cual se produce la acumulación (longitud de barrera rellena), [m]
Ka: factor de empuje activo (fig. 6)
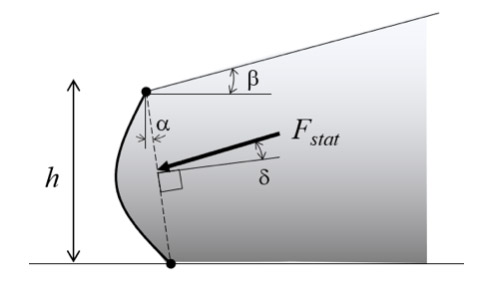
Fig. 6. Evaluación de Ka según Coulomb.
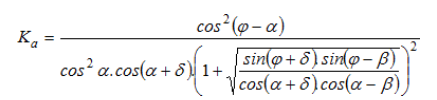
Ka factor de empuje activo
β inclinación del material acumulado en el trasdós respecto a la horizontal, [º]
δ rozamiento entre el material y trasdós, inclinación de Fstat respecto a la normal, [º]
α inclinación de la barrera respecto a la vertical, [º]
Φ ángulo de fricción interna del material, [º]
Siguiendo la simplificación de Rankine, el factor de empuje activo lateral, considerando β, δ yα = 0, el factor de empuje activo solo depende del ángulo de fricción interna del material Φ, quedando:
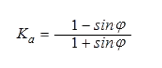
Cables de soporte perimetral
Las fuerzas se trasmiten de la malla o red de interposición (anillos o rombos) a los cables de soporte perimetral y se dividen en los diferentes cables de forma proporcional al área neta limítrofe (Roth 2003). Además, son repartidas al 50% en los cables de soporte perimetral, si hay presentes dos de ellos. La fuerza total sobre el cable se transforma en una fuerza q distribuida uniformemente por metro lineal (fig. 7).
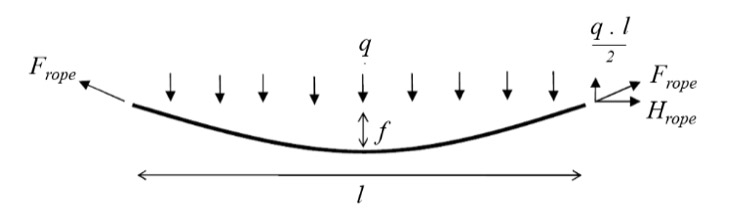
Fig. 7. Carga q uniformemente distribuida.
En primer lugar, se determina la longitud de instalación del cable S0, que depende de la longitud del tramo l y de la máxima flecha en el cable f (Palkowski 1990), cuyos valores típicos para el proceso de llenado están entre de 1/50 a 1/30 del tramo l [m].
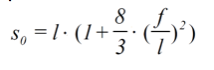
La deformación del cable se puede despreciar porque es muy pequeña (~2,5‰) en comparación con la elongación o alargamiento de este, como resultado del empleo de los elementos de frenado (los frenos pueden ser de anillos tubulares o en U). La longitud del cable deformada se determina de la siguiente manera:
S1 = S0 + n. bu
donde:
n: número de frenos involucrados
bu: es la elongación máxima de freno [m]
Posteriormente, se puede calcular la fuerza en el cable mediante la cual la carga q es distribuida en [N/m] (Palkowski 1990). Hrope se refiere a la componente de la fuerza del cable Frope en dirección del eje inicial del cable.
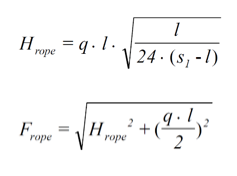
Los cables de soporte inferior se desplazan principalmente en dirección horizontal, mientras que el cable de soporte superior también se desplaza verticalmente. En consecuencia, la fuerza en el cable de soporte superior tiene que incrementarse para considerar este efecto. Finalmente, las fuerzas de los cables se comparan con las cargas mínimas de frenado de los cables considerando un factor de seguridad. Hay que tener en cuenta que también los elementos de frenado deben ser capaces de soportar las fuerzas esperadas en los cables.
Cables de retención al monte
Las fuerzas en los cables de retención se pueden determinar utilizando un equilibrio estático en las cabezas de los postes (fig. 8). Al hacerlo, solo se deben considerar las componentes horizontales, porque las verticales son soportadas por los postes (axil actuante, a revisar según 6). Las solicitaciones de mayor entidad ocurren en los postes extremos.
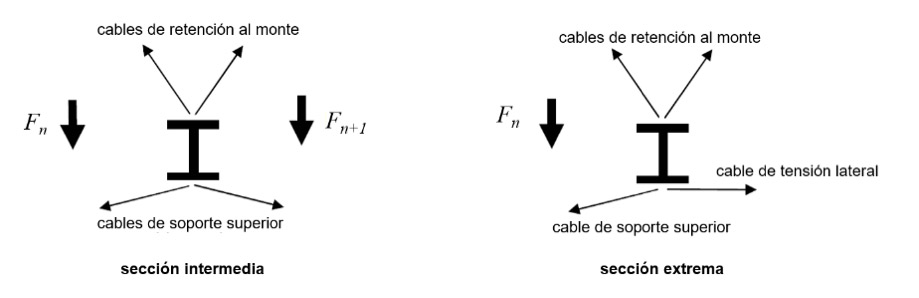
Fig. 8. Distribución de cargas en las cabezas de los postes (secciones intermedia y extrema).
Utilizando las fuerzas en los cables que actúan sobre la cabeza del poste, es posible calcular las fuerzas actuantes en los cables de retención al monte (fig. 8). Hay que tener en cuenta que los cables de retención están inclinados en dos direcciones.
Anclajes flexibles
Con el dimensionamiento del anclaje, se debe demostrar que las fuerzas en los cables se pueden transferir al terreno. Con las fuerzas en los cables de soporte y bajo la consideración de factores de seguridad, se pueden elegir anclajes adecuados. Los ensayos de campo desarrollados demuestran que las solicitaciones dinámicas en los anclajes son superiores a las estáticas. Por lo tanto, los anclajes deben estar equipados con cabezales de anclaje flexibles con un rango de ±30º (fig. 9).
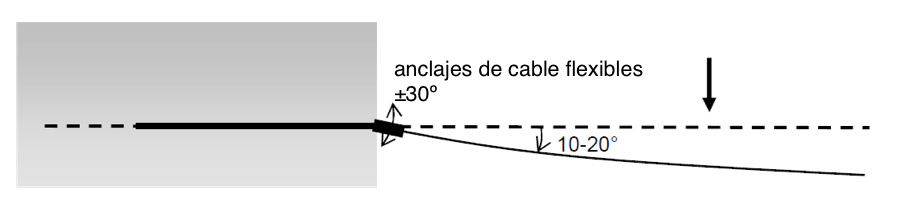
Fig. 9. Anclajes de cable flexibles.
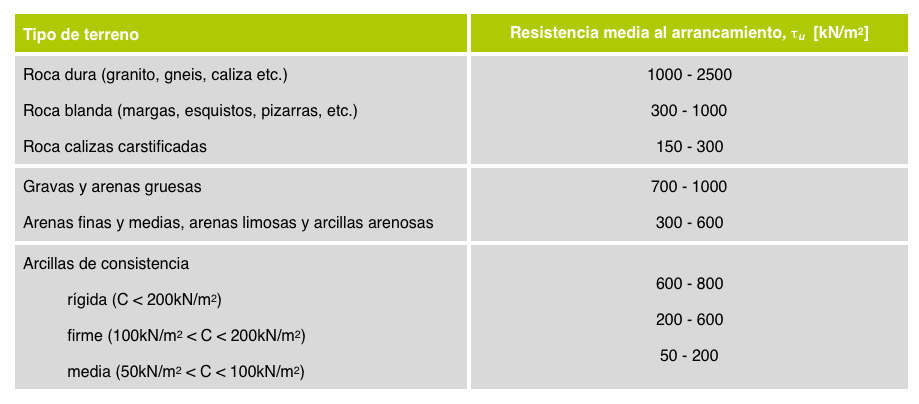
Debe asegurarse que el terreno pueda soportar las solicitaciones, para las adherencias mínimas, se sugiere utilizar la recomendación del Manual de Anclajes en Ingeniería Civil (Ucar 2005). En caso de duda, se deben realizar ensayos de arrancamiento (Tabla 2).
Membrana de interposición
La fuerza más alta en la red o malla de interposición (anillos o rombos) ocurre en el centro de la barrera, donde presuntamente el conjunto de rocas golpea primero. La fuerza estática Fstat se transforma en una carga q1 distribuida verticalmente de manera uniforme de acuerdo con el ensamblaje de cables (fig. 10).
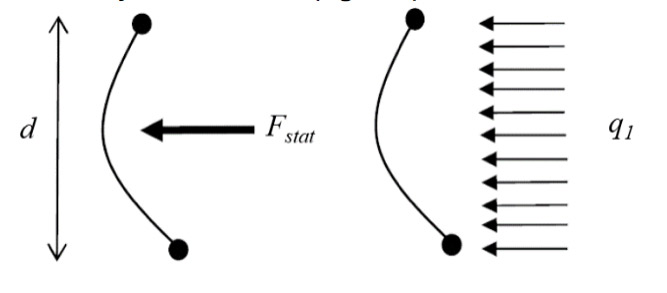
Fig. 10. Carga distribuida tras la red (sección transversal).
Para facilitar los cálculos, se asume que las membranas durante el proceso de frenado de una carga distribuida se deforman elásticamente entre un 20%-30% (Luis 2011).
d1 = 1,2-1,3. d
Posteriormente, la carga en la red se puede determinar de la siguiente manera, donde q1 se refiere a la carga distribuida uniformemente en la red en [N/m] (Palkowski 1990).
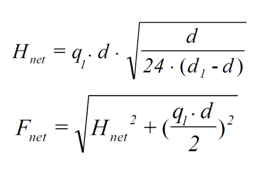
Con el valor de la carga, es posible dimensionar la membrana de interposición y los grilletes con los que esta está unida a los cables de soporte perimetral. Para este propósito, la carga actuante se compara con el valor de rotura y la capacidad de los grilletes, con un factor de seguridad.
Revisión por pandeo de los postes (SE-A 2008 / NBE EA-95)
Se denomina esbeltez reducida a la raíz cuadrada del cociente entre la resistencia plástica de la sección de cálculo y la compresión crítica por pandeo (González 2007), de valor:
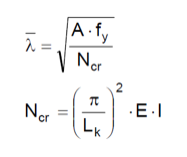
donde:
A: área de la sección transversal, [mm2]
fy: límite elástico del acero, [MPa]
Ncr: axil crítico, [kN]
E: módulo de elasticidad, [MPa]
I: momento de inercia del área de la sección para flexión en el plano considerado, [mm4]
Lk: longitud de pandeo (altura del poste), equivalente a la distancia entre puntos de inflexión de la deformación de pandeo, [m]
El coeficiente χ de reducción por pandeo, para valores de la esbeltez reducida ≥ 0,2 se obtiene de:
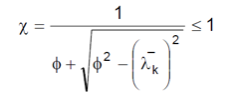
donde
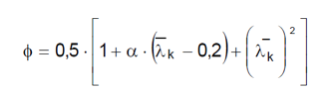
α: es el coeficiente de imperfección elástica, que adopta los valores de la Figura 9 en función de la curva de pandeo (tabla 1). Esta representa la sensibilidad al fenómeno dependiendo del tipo de sección, plano de pandeo y tipo de acero, de acuerdo con la tabla 1.
Los valores del coeficiente χ se pueden obtener directamente de la Figura 11 o en función de la esbeltez reducida y del coeficiente de imperfección, respectivamente.
Luego el máximo axil absorbido por el soporte será:
Nb = χ. A. fyd
fyd = fy. γM1
siendo:
γM1 coeficiente de seguridad
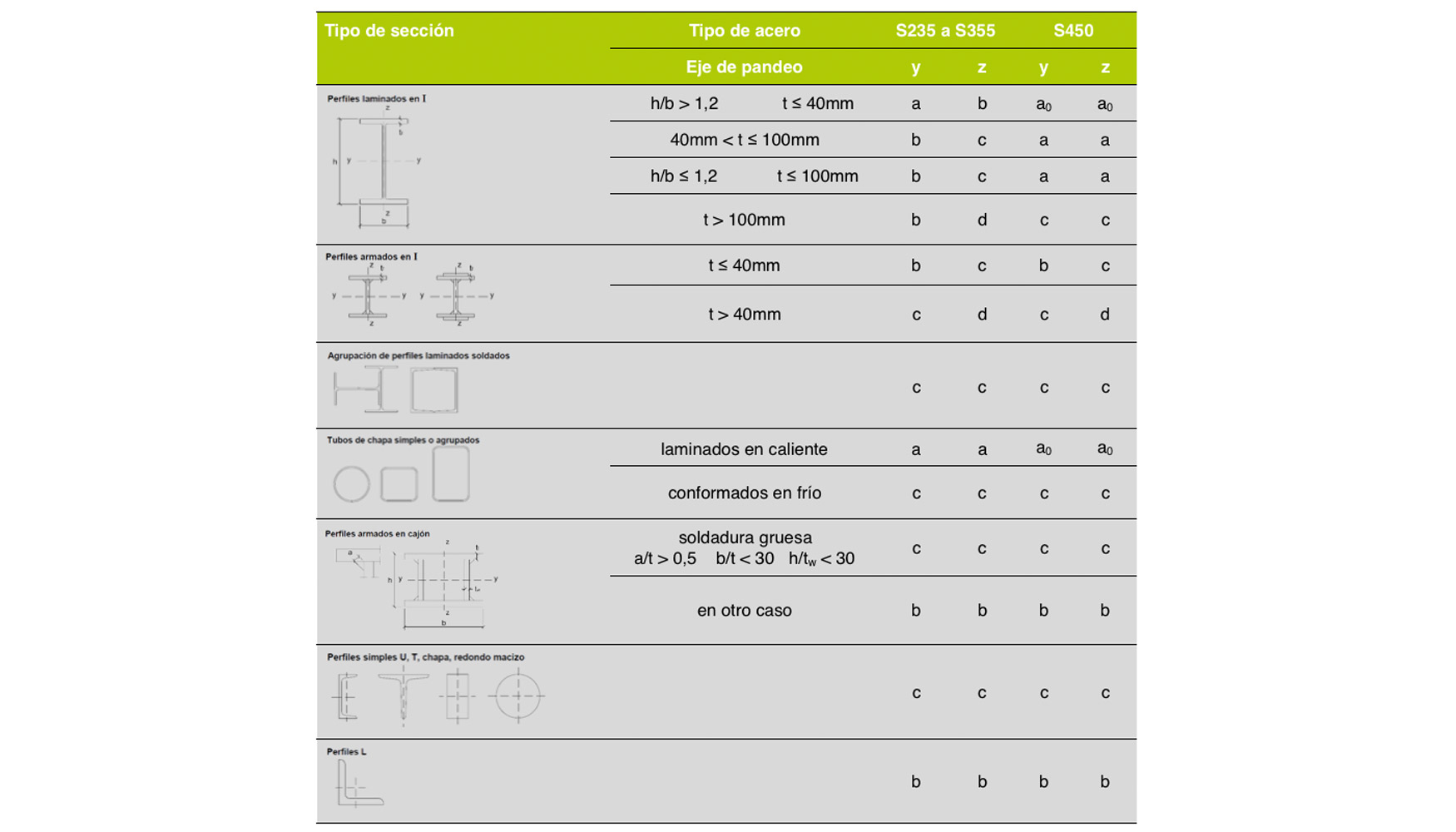
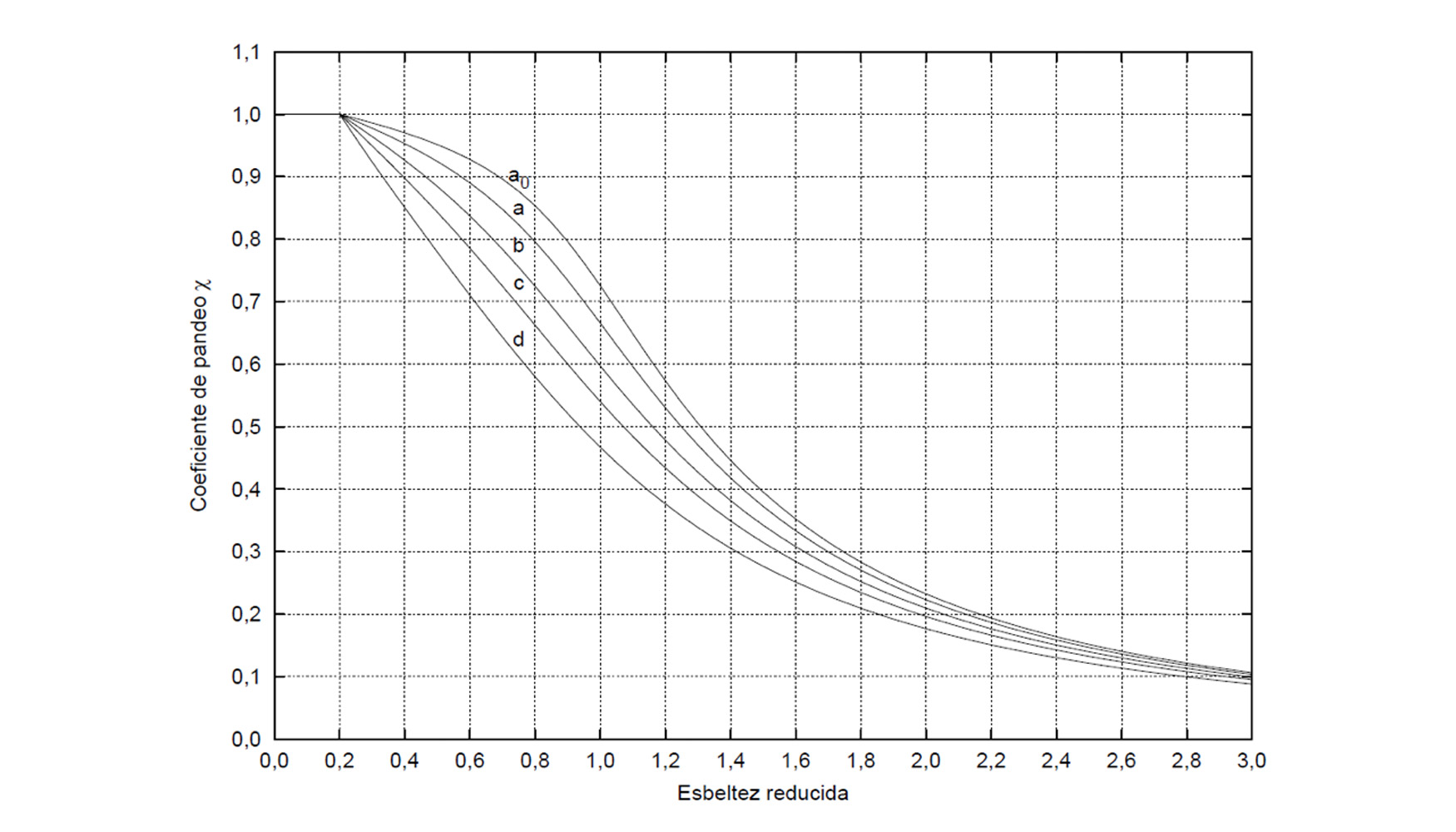
Fig. 11. Curvas de pandeo.
Conclusiones
Las barreras flexibles de protección contra desprendimientos son una solución extremadamente eficiente desde el punto de vista técnico-económico, a problemas de inestabilidad en bloques que se desprenden de las zonas altas de taludes o laderas. Esta solución no es solo efectiva ante importantes cargas dinámicas, sino que también puede ser extremadamente útil en casos donde se produzcan combinaciones de carga o predomine la carga estática, por razones de explotación. Resulta importante en el proceso de diseño tener claras la hipótesis de partida y en caso necesario hacer una revisión de las solicitaciones estáticas, a partir de las necesidades del proyecto en concreto. La metodología explicada, permite de forma simple poder realizar el proceso de dimensionamiento de los principales componentes de las barreras flexibles, consiguiendo que sean también efectivas ante las solicitaciones estáticas.
Referencias
- González, A. (2007) Soportes simple de acero sometidos a compresión centrada.
- Luis, R., Prieto, J., Raïmat, C., y Sanz, A. (2011) Efecto negativo del empleo de redes ASM de anillos de alambre de acero en la estabilización de taludes. Ingeopres 184. Madrid
- Muraishi, H., Sano, S. (1997) Full scale rockfall testing of ring net barrier and component. Japan
- NBE EA-95 (1995) Estructuras de acero en edificación. MOPTMA
- Palkowski, S. (1990), Statics of rope constructions, Springer, Berlin
- Roth, A., Wartmann, S. (2003) Protection system against Debris Flow. Design concept. Suiza
- SE-A (2008) Seguridad estructural del Acero. BOE 25/01/2008
- Ucar, R. (2005) Manual de anclajes en Ingeniería Civil. Madrid
- Wendeler, C. (2016) Debris-Flow Protection System for Mountain Torrents. WSL. Suiza