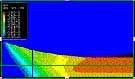
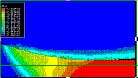
Analizada en la laminación plana en frío del aluminio AA 3004-H19

El grado de homogeneidad de la deformación inducida en el material durante la laminación tiene una notable influencia en la evolución del propio proceso, así como en las propiedades finales del producto. La falta de homogeneidad en la deformación se manifiesta, por ejemplo, en la distribución de presiones en el contacto rodillo-lámina, presentando una evolución totalmente diferente a la observada bajo condiciones homogéneas. De esta evolución dependen las tensiones residuales que aparecen finalmente en la lámina metálica, las cuales afectan decisivamente tanto a las propiedades en servicio como a la integridad del producto. El presente trabajo muestra un análisis termo-mecánico 2D mediante el Método de los Elementos Finitos (MEF) del proceso de laminación plana en frío del aluminio AA 3004-H19. Dicho trabajo se centra en analizar las distribuciones de tensión en el contacto rodillo-lámina, así como las tensiones residuales en la lámina, para diferentes grados de homogeneidad de la deformación

Dada la especial relevancia que el proceso de laminación plana tiene a nivel industrial, el estudio de la influencia de los parámetros y variables del proceso ha recibido una especial atención y esfuerzo investigador durante el último medio siglo. Dichos trabajos ponen de manifiesto la existencia de diferentes patrones en la evolución de las presiones en el contacto rodillo-lámina durante la laminación plana, dependiendo de la homogeneidad de la deformación inducida en el material [1-5].

Cuando la deformación es homogénea, las presiones de contacto muestran un único máximo debido al efecto de la fricción y localizado en el punto neutro (Figura 1 a). Esta evolución se corresponde con la predicha por las teorías clásicas, por ejemplo las de Orowan [1] y Bland y Ford [2] entre otros, las cuales permiten una estimación razonable de las variables del proceso. El grado de homogeneidad de la deformación puede cuantificarse mediante el parámetro H propuesto por Li y Kobayashi [5] como H = R / h0 * r siendo h0 el espesor inicial de la lámina, R el radio de los rodillos y r la reducción de espesor (r = Dh / h0). En los casos de deformación homogénea el parámetro H toma valores superiores a 3 [5]. Sin embargo, cuando las condiciones de laminación son tales que la deformación impuesta en el material deja de ser homogénea, esto es, H < 3, la distribución de presiones presenta dos máximos, situados próximos a las zonas de entrada y salida respectivamente (Figura 1 b), como ponen de manifiesto los trabajos experimentales de MacGregor y Palme [3] y Al-Salehi et al. [4]. Finalmente, los resultados de MacGregor y Palme [3] muestran que a medida que la deformación se hace menos homogénea las presiones pasan a mostrar de nuevo una distribución de un sólo máximo, pero esta vez situado muy próximo a la zona de entrada. En estas últimas situaciones, el uso de las teorías clásicas, deducidas en su mayoría bajo la hipótesis de deformación homogénea, no son a priori adecuadas para analizar el proceso de laminación, siendo necesario recurrir a otras técnicas, entre ellas las numéricas, e.g. el MEF.

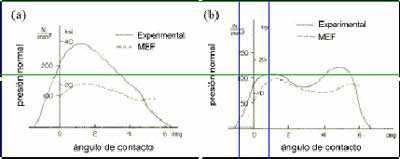
Figura 1. Distribución de presiones en el contacto: (a) Deformación homogénea (H=13,1) y (b) Deformación no-homogénea (H=1,79) [resultados experimentales de Al-Salehi et al. (1973) [4] y resultados numéricos (MEF) de Li y Kobayashi (1982) [5].

El número de trabajos existentes en la literatura dedicados al estudio del proceso de laminación y las características del producto en condiciones de deformación no homogénea es relativamente escaso. El presente trabajo intenta ahondar en el conocimiento de esta última situación, presentando un estudio numérico sobre el proceso de laminación plana en frío en el rango de H < 3 y bajo condiciones de fricción moderadas. Se han obtenido y analizado las distribuciones de tensiones normales y tangenciales en el contacto rodillo-lámina, así como la evolución de las tensiones residuales que aparecen en el producto laminado, para diferentes valores del parámetro H. El material modelado ha sido la aleación de aluminio AA 3004-H19, de extendido uso industrial, especialmente en piezas embutidas.

Haciendo uso del paquete comercial de elementos finitos ABAQUS [6], se ha realizado un modelo 2D del conjunto rodillo-lámina, bajo la hipótesis de deformación plana. Ambos elementos se consideran deformables, empleándose para su análisis la teoría de grandes deformaciones. Así mismo, se ha supuesto el proceso de laminación como un proceso cuasi-estático, resolviendo el problema termo-mecánico acoplado en forma incremental, desde la entrada de la lámina entre los rodillos hasta alcanzar el régimen estacionario, para diferentes reducciones (i.e. diferentes valores de H). Los parámetros geométricos y condiciones iniciales empleados han sido: espesor inicial de la lámina (h0) de 20 mm, rodillos de 70 mm de radio, velocidad de giro de 30 rpm y temperatura inicial del conjunto 20ºC.

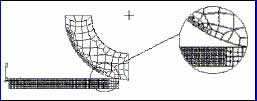
Figura 2. Malla de elementos finitos empleada.

El material de trabajo modelado ha sido la aleación de Aluminio AA 3004-H19. Para dicho material se ha supuesto un comportamiento elasto-plástico con endurecimiento isotrópico. Dado el rango de temperaturas esperables en procesos de laminación en frío, se ha considerado despreciable la influencia de la velocidad de la deformación. Las propiedades mecánicas y térmicas adoptadas se resumen en la Tabla 1 [7,8]. Los rodillos se han supuesto de acero, con comportamiento elástico lineal. Las propiedades mecánicas y térmicas empleadas han sido las siguientes (E=210 GPa, n=0,3, Cp=460,5 J/kgK, k=52 W/mK, a=1,2·10-5 m/mK).

La Figura 2 muestra la malla empleada en las simulaciones. Dada la simetría del conjunto sólo se ha modelado la mitad del mismo. Se han empleado elementos cuadriláteros de 4 nodos, lineales en desplazamientos y en temperatura (tipo CPE4T en notación de ABAQUS). Para reducir el volumen del modelo, el centro del rodillo se ha considerado rígido y sólo se ha discretizado una corona exterior de espesor 30 mm (véase Figura 2).

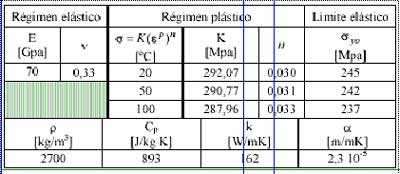
Tabla 1. Propiedades mecánicas y térmicas para el AA 3004-H19.

En la zona de contacto rodillo-lámina se ha supuesto una ley de rozamiento del tipo Coulomb. El coeficiente de fricción empleado ha sido µ = 0,3. Se ha tenido en cuenta tanto el calor generado por deformación plástica como el generado por fricción. Como es habitual, se ha considerado que el 95% del trabajo plástico se transforma en calor. Así mismo, se ha supuesto que el trabajo de rozamiento se transforma íntegramente en calor y que éste se distribuye equitativamente entre las superficies en contacto. Finalmente, se ha tenido en cuenta en los cálculos la conducción de calor a través de las superficies de contacto rodillo-lámina. No obstante, el intercambio de calor con el ambiente no se ha incluido.

A continuación se muestran los resultados obtenidos con el modelo numérico descrito anteriormente, destacando las diferencias más relevantes respecto a las situaciones de deformación homogénea. En la Tabla 2 se recogen las reducciones r analizadas y sus correspondientes valores del parámetro H.

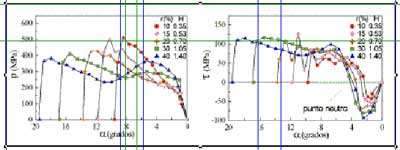
La Figura 3 muestra la distribución de presión (p) y de tensión tangencial (t) en la zona de contacto para valores de H de 0,35; 0,53; 0,70; 1,05 y 1,40. En la citada figura se puede observar que, para H igual a 1,40 y 1,05, la distribución de presión muestra claramente dos máximos, de acuerdo con los resultados experimentales de MacGregor y Palme [3] y Al-Salehi et al. [4], así como con la cota propuesta por Li y Kobayashi [5] (H > 3). El trabajo de MacGregor y Palme [3] muestra que el primer máximo (zona de entrada) es debido a la restricción a la deformación plástica impuesta por el material en régimen elástico circundante a la entrada de los rodillos. Dicha restricción hace que la presión necesaria para deformar el material aumente, análogamente a lo que ocurre en la indentación de un material (e.g. en un ensayo de dureza). Dicho efecto ha sido referido por Orowan como "peening effect". El máximo a la salida en cambio parece ser consecuencia del endurecimiento por deformación que exhibe el material. No obstante, esta configuración de dos máximos desaparece a medida que H decrece por debajo de la unidad. En el rango de H < 1 , se observa que a medida que H decrece el máximo de la zona de entrada comienza a aumentar, mientras que el máximo de la zona de salida disminuye, apareciendo así un único pico en la distribución de presiones situado claramente a la entrada. En dichas situaciones, como se observa en las distribuciones de tensión tangencial (véase Figura 3), la posición del punto neutro no se corresponde con la posición de ninguno de los máximos de la presión de contacto, al contrario de lo que ocurre cuando la deformación es homogénea (H > 3). Esta transición entre la configuración con dos máximos a la de un solo máximo a la entrada encontrada en la presión de contacto puede observarse también en los resultados experimentales de MacGregor y Palme [3], obtenidos para diferentes materiales, tales como aluminio (99,54% Al), cobre (99,92% Cu), acero (SAE 1020). Como se verá en lo que sigue, dicha transición de dos picos a uno solo parece tener una importante repercusión en la evolución de las tensiones residuales que aparecen en la lámina.

Tabla 2. Reducciones r (%) y valores de H analizados.

Figura 3. Evolución de la presión (p) y la tensión tangencial (t) en el contacto rodillo-lámina para diferentes reducciones vs. el ángulo de contacto a

(a = 0º ’ salida).

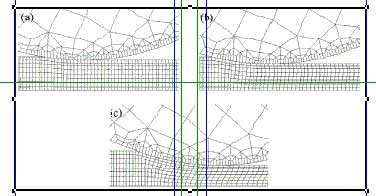
Figura 4. Deformación de la malla:

(a) r=10% (H=0,35)

(b) r=20% (H=0,70)

(c) r=40% (H=1,40)

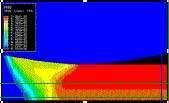
La Figura 4 presenta la deformación sufrida por la malla para las reducciones del 10, 20 y 40% respectivamente. Asimismo, las Figuras 5, 6 y 7 muestran las distribuciones de deformación plástica equivalente y de temperatura existentes en la lámina para estas mismas reducciones. Como se puede apreciar, la deformación plástica se concentra predominantemente en la región superficial y subsuperficial de la lámina, lo cual es característico en las situaciones de deformación no homogénea (H < 3). En particular, se observa que, para el 40% de reducción (H = 1,40), la mayor deformación plástica se produce claramente en la superficie. Mientras que para las reducciones del 20% (H = 0,70) y 10% (H = 0,35) es la región subsuperficial la que presenta una mayor deformación plástica. Esto es debido a que al disminuir la reducción crece la importancia relativa de la restricción a la deformación debida a la fricción en las superficies en contacto. Dicho patrón de deformación influye directamente en la evolución de las tensiones residuales.

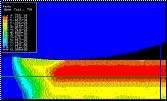
Figura 5a. Distribución de la deformación plástica equivalente (epeq) para r =10% (H=0,35).

Valor máximo: epeq ≈ 17%

Figura 5b. Distribución de temperaturas (T) para r =10% (H=0,35).

Valor máximo: T ≈ 34 ºC

Figura 6a. Distribución de la deformación plástica equivalente (epeq) para r =20% (H=0,70).

Valor máximo: epeq ≈ 30%

Figura 6b. Distribución de temperaturas (T) para r =20% (H=0,70).

Valor máximo: T ≈ 46 ºC

Figura 7a. Distribución de la deformación plástica equivalente (epeq) para r =40% (H=1,40).

Valor máximo: epeq ≈ 75%

Figura 7b. Distribución de temperaturas (T) para r =40% (H=1,40).

Valor máximo: T ≈ 79 ºC

La Figura 8 muestra la evolución de los valores máximos y valores en la superficie de las tensiones residuales normales sxx en la lámina (x=dirección de laminación) en función de H. Se observa que a medida que H disminuye el valor de las tensiones residuales aumenta, hasta alcanzar un máximo para H entre 0,07 - 0,18 (2% < r < 5%). Este comportamiento se justifica atendiendo al hecho de que al disminuir H se induce en la lámina una deformación cada vez menos homogénea y, por tanto, para compatibilizar dicha deformación deben aparecer localmente tensiones residuales más elevadas. No obstante, para valores de H muy bajos, es decir, reducciones muy pequeñas, aún siendo la deformación menos homogénea, los niveles de deformación son tan bajos que las tensiones residuales disminuyen paulatinamente hasta anularse para r igual a cero como es de esperar (véase Figura 8). Otro hecho que es importante destacar es que, para H ≥ 1,05 (r ≥ 30%) las tensiones residuales en la superficie son de compresión, mientras que el máximo de estas, de tracción obviamente, se produce en la subsuperficie. Este patrón en las tensiones residuales es consecuencia directa de que las máximas deformaciones plásticas se concentren en la superficie de la lámina, como se ha comentado anteriormente. Por otro lado, para valores de H ≤ 0,7 (r ≤ 20%), se observa que las tensiones residuales en la superficie pasan a ser de tracción, encontrándose la máxima tensión residual en la zona subsuperficial o en la propia superficie dependiendo del valor de H. Como se apuntó anteriormente, este cambio de signo en las tensiones residuales de la superficie coincide exactamente con el paso de la configuración de dos máximos a la de un único máximo a la entrada observada en la distribución de las presiones de contacto. Predecir el valor y distribución de las tensiones residuales es un aspecto de gran importancia práctica, ya que éstas influyen decisivamente en la aparición de defectos superficiales en la lámina (e.g. agrietamiento), en el comportamiento de la lámina frente a posteriores procesos de fabricación y en el comportamiento en servicio del producto laminado (e.g. comportamiento a fatiga, corrosión, etc.).

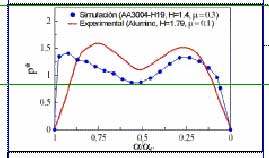
Figura 9. Presión adimensional p* vs. ángulo de contacto normalizado:

• simulación con H =1,4 (ac ≈ 19,44º)

ensayos de Al-Salehi et al. [4] (H =1,79, ac ≈ 7,6º)

Finalmente, dada la falta de resultados experimentales específicos sobre la laminación del aluminio AA 3004-H19, para validar el modelo empleado se han comparado algunos de los resultados de las simulaciones con resultados experimentales existentes en la literatura para materiales y situaciones parecidas. Para que tal comparación sea factible esta se debe hacer empleando variables adimensionales. La Figura 9 muestra una comparación de los resultados obtenidos con la simulación para H = 1,4 y los resultados experimentales obtenidos por Al-Salehi et al. [4] para Aluminio con un valor de H similar, H = 1,79. En dicha figura se muestra la distribución de presiones adimensionalizada, p* = p /s–Y, frente al ángulo a normalizado por el ángulo total de contacto (ac). En la expresión anterior, s–Y es la tensión de flujo promedio en el material, la cual representa la resistencia media a la deformación plástica interpuesta por el material durante el proceso de laminación. Para el material y condiciones de la simulación, s–Y tiene un valor de 273 MPa¸ mientras que para los ensayos de Al-Salehi et al. el valor fue estimado de las gráficas de los propios autores en 78 MPa [4]. Como se puede observar en la Figura 9, la evolución de p* presenta una excelente coincidencia tanto en la posición y como en los valores de los máximos, especialmente a la salida. La máxima diferencia entre ambas curvas es inferior a un 14%. Dicha comparativa pone de manifiesto dos hechos de interés. Por un lado muestra la probada independencia de las presiones de contacto respecto del valor del coeficiente de fricción en el rango de deformación no homogénea [3, 9]. Nótese que el coeficiente de fricción empleado en las simulaciones de este trabajo ha sido µ = 0,3, mientras que el medido por Al-Salehi et al. en sus ensayos fue de µ ≈ 0,1. Por otro lado, dichos resultados sugieren la existencia de cierto grado de escalabilidad entre los resultados obtenidos con diferentes aleaciones de Aluminio, siempre que los valores de H, al menos en el rango de H < 3. No obstante, esta última afirmación debe ser objeto de un estudio más detallado.

El presente trabajo presenta un estudio bidimensional mediante el MEF del proceso de laminación plana en frío del aluminio AA 3004-H19, bajo condiciones de deformación no homogénea (H < 3) y fricción moderada (µ = 0,3). En particular se analizan los efectos que una deformación no homogénea en el material induce tanto en las distribución de tensiones en el contacto como en las tensiones residuales que aparecen en la lámina. Las conclusiones que se extraen de este trabajo se pueden resumir como sigue:

• En aquellas situaciones en las que 1 < H < 3, las presiones en el contacto presentan dos claros máximos situados a la entrada y la salida respectivamente, de acuerdo con los ensayos experimentales de MacGregor y Palme [3] y de Al-Salehi et al. [4].

• Para valores de H entorno a la unidad se observa que el máximo situado en la zona de la entrada comienza a predominar. Así, para H < 1, la distribución de presiones presenta un único máximo situado en la zona de entrada, lo cual está en perfecto acuerdo con los resultados experimentales de MacGregor y Palme [3].

• En las situaciones de deformación homogénea (H << 3), donde existe un único máximo en las presiones de contacto, la posición del punto neutro está determinada por la posición de dicho máximo. No obstante, esto no sigue siendo válido cuando la deformación deja de ser homogénea. En particular, para H < 1, la posición del máximo a la entrada no está definida por la posición de punto neutro.

• El valor de las tensiones residuales sxx aumenta al disminuir H, alcanzando un máximo de tracción para H entre 0,07 - 0,18 (2% < r < 5%).

• Se observa un cambio de signo en las tensiones residuales superficiales, de compresión a tracción, que coincide con el paso de la configuración de dos máximos a la de un solo máximo a la entrada observada en las presiones de contacto.

Los autores desean expresar su agradecimiento a D. Ramón A. Ortiz Vargas-Machuca por su colaboración en las tareas de simulación numérica del presente trabajo

[1] E. Orowan, The Calculation of Roll Pressure in Hot and Cold Flat Rolling, Proc. I. Mech. E., Vol. 150 (1943), p. 140.

[2] D.R. Bland and H. Ford, The Calculation of Roll Force and Torque in Cold Strip Rolling with Tension, Proc. I. Mech. E., Vol. 159 (1948), p. 144.

[3] MacGregor C. W. and Palme R. B., The Distribution of Contact Pressures in the Rolling of Metals, Trans. ASME, J. Basic Engng., Vol. 81 (1959) p. 669.

[4] F.A.R. Al-Salehi, T.C. Firbank and P.R. Lancaster, An Experimental Determination for the Roll Pressure Distributions in Cold Rolling, Int. J. Mech. Sci., Vol. 15 (1973) p. 693.

[5] G. Li and S. Kobayashi, Rigid-Plastic Finite-Element Analysis of Plane Strain Rolling, J. Eng. Ind., Vol. 104 (1982), p. 55.

[6] ABAQUS/ Standard. Hibbitt, Karlsson and Sorensen, Inc., Providence, (1998).

[7] D. Park and J.G. Morris, The Tensile Deformation Behavior of AA3004 Aluminum Alloy, Metall. Trans. A, Vol. 25 (1994), p. 357.

[8] Metals Handbook Ninth Edition, Vol. 2, ASM, Ohio (1978).

[9] G.E. Dieter, Mechanical Metalurgy (SI Metric Edition), McGraw-Hill Series in Materials and Engineering, UK (2001).