Ajuste óptimo de controladores para la compensación de no-linealidades en servomecanismos

El nivel de competitividad en el campo de la fabricación impone el desarrollo de controles numéricos con mejores prestaciones, mayores precisiones, más flexibles y con mayor valor añadido como vía para la diferenciación en el mercado. La mejoría en la precisión de los servomecanismos pasa ineludiblemente por una mejor compensación de las no linealidades inherentes a estos sistemas. Gana importancia, por tanto, el modelado de no linealidades duras como la fricción, como base para el desarrollo ulterior de sistemas de compensación que se traduzcan en un mejor comportamiento del sistema de control. De hecho, gracias al modelado de las no-linealidades se pueden realizar ajustes óptimos de los reguladores que conllevan un mejor desempeño en la precisión de los CNC. El presente trabajo presenta una optimización a través del método de Nelder-Mead de los parámetros del regulador P-PI en cascada del lazo de control de velocidad y de posición de un servomecanismo en presencia de fricción, elasticidad y holgura. El trabajo trata de demostrar cómo a través de un ajuste óptimo de los lazos de control se puede reducir el error de seguimiento del CNC en la ejecución de diversas trayectorias a distintas velocidades.

La fuerte competencia a nivel internacional en el sector metal-mecánico obliga a desarrollar e implantar Controles Numéricos por Computador (CNCs) que mejoren los procesos productivos en todas sus facetas, por ejemplo, aumentando las tasas de arranque del material, disminuyendo los tiempos de parada, mejorando la calidad superficial, mejorando la calidad dimensional, protegiendo la herramienta de corte, conservando la mecánica de la máquina, etc. A su vez, los propios CNCs han de ser capaces de sacar el mayor rendimiento posible y aumentar las prestaciones de las propias máquinas de corte, así como de sus elementos asociados [1].

Por otra parte, a pesar de los grandes progresos en áreas como la Ciencia de los Materiales, la mecánica de precisión y la electrónica, en la actualidad las no linealidades siguen afectando a más del 60% del par motor de motores eléctricos. Más concretamente, las no linealidades duras debidas a la Fricción de Coulomb y a la fricción estática degradan seriamente el rendimiento de los sistemas de control, ya que afectan casi al 30% del par motor en una amplia gama de sistemas electromecánicos existentes en la industria [2].

Desde hace varias décadas, la ingeniería de control ha permitido un análisis y ha propiciado el desarrollo de técnicas para compensar las no linealidades duras. Para ello se han realizado grandes esfuerzos en tratar de modelizar el comportamiento de las mismas. Sin embargo, la formalización matemática exacta con un enfoque físico completo no es trivial y, en algunas ocasiones, el modelado de la no-linealidad es parcial o incompleto. De este modo, una posible solución está basada en la utilización de diferentes modelos para representar de forma aproximada la fricción, la holgura o la elasticidad. A su vez, la introducción de herramientas para representar sistemas no lineales permitió el desarrollo fructífero de un campo dentro de la Automática que se conoce generalmente como la Teoría de Control No Lineal. La búsqueda de una ley de control para un sistema no lineal ha supuesto la aparición de una rica amalgama de técnicas de control.

Diferentes leyes de control como retroalimentación de estados, linealización por realimentación, planificación de ganancia, etc. son algunas de las soluciones particulares empleadas en el control de servomecanismos para abordar la problemática de control sobre sistemas no lineales [3]. Cuando se está en presencia de un sistema con una alta no-linealidad, debido por ejemplo al fenómeno de la fricción, pueden utilizarse también algoritmos de control adaptable y control PD robusto con la finalidad de obtener una mejor solución del sistema a controlar [4]. Sin embargo, desde el punto de vista de la aplicación tecnológica, estas técnicas suelen conducir a leyes de control muy complejas y de alto coste computacional en su implementación. Por esta razón, no suelen ser implementadas en la mayoría de los CNCs comerciales.

Este trabajo aborda la problemática de la compensación de no-linealidades en servomecanismos desde un punto de vista diferente: la sintonía óptima de los parámetros de control. El empleo de estrategias de optimización como la que se sugiere en este trabajo puede resultar de gran utilidad si se dispone de un modelo aproximado del proceso y de las no-linealidades. Además, desde el punto de vista computacional, el ajuste óptimo de los parámetros de los sistemas de control de procesos complejos puede ser más eficiente que el empleo de técnicas no lineales ya que no implica cambios en la estructura del controlador, acortando las fases de diseño y puesta a punto. Es necesario, no obstante, elegir una función de coste o índice de desempeño adecuado y especificar un procedimiento de optimización para que sea comprensible y aplicable por técnicos y profesionales.

Hoy en día, están disponibles una amplia gama de métodos determinísticos y estocásticos para abordar problemas de optimización. Se encuentra fuera del alcance de este trabajo analizar y comparar todos los métodos de optimización libres de gradiente disponibles en la literatura. En este trabajo se ha optado por la utilización del método de Nelder-Mead [5]. El principal argumento es que es que el algoritmo básico es relativamente fácil, además de su comprensión, por lo que se ha hecho muy popular en muchos campos de la ciencia y la tecnología.

Es importante señalar, que los trabajos relacionados con la sintonía óptima y la optimización para mejorar las prestaciones de los sistemas de control y compensar las no-linealidades en servomecanismos, no son muy frecuentes en la literatura a la que se ha tenido acceso. Kuo y Yen [6] proponen un sistema para el ajuste simultáneo de los parámetros del control del movimiento de una máquina de CNC con cinco ejes basándose en un algoritmo genético. Sin embargo, este trabajo se centra solo en la fricción, despreciando el resto de no-linealidades. Interesante resulta también el trabajo de Aggarwal and Singh, en el que se hace una revisión de técnicas de optimización aplicadas al mecanizado [7]. Además, se repasan técnicas como métodos de Lagrange, optimización genética, algoritmos genéticos, o el método de Taguchi entre otras, aplicadas a la optimización de parámetros en este campo. Sin embargo, estas optimizaciones no están relacionadas directamente con las nolinealidades y los servomecanismos.

El presente artículo se organiza de la siguiente manera, en el apartado 2 se muestran algunas de las no-linealidades inherentes a los servomecanismo, ofreciendo diversas propuestas para el modelado de las mismas. En el apartado 3, se analiza ya el esquema de control particular del servomecanismo sobre el que se van a realizar las optimizaciones. En el apartado 4 se ilustra el método de optimización elegido, mientras que el apartado 5 ofrece los resultados en simulación obtenidos a través de la optimización. Por último, en el apartado 6 se esbozan algunas conclusiones.

Las tres no-linealidades básicas que predominan en la observación empírica del comportamiento de los sistemas electromecánicos son la fricción, la holgura y la elasticidad. El término fricción es usado en términos generales para indicar las distintas relaciones existentes entre la velocidad y/o la fuerza con las disipaciones de energía en un dispositivo. La holgura denota la histéresis mecánica así como determinados impactos en los cuerpos mecánicos. La elasticidad es el término contrario a la rigidez y se refiere a la deformación en los elementos de transmisión de la máquina. La literatura examina estos efectos individualmente o como resultado de la combinación de dos de ellos aunque, ciertamente, todos ellos están inherentemente relacionados. En la mayoría de las publicaciones científicas se exponen métodos de compensación, algunos basados en modelo y otros no. Sin embargo, antes de profundizar en el tema de la compensación, es necesario contar con un modelo de las mismas. En este apartado se muestra una pequeña revisión del estado del arte en cuanto a modelos de fricción y de holgura, dos de las no-linealidades más importantes y más estudiadas en el control de servomecanismos.

2.1 Fricción

Respecto al modelado y su compensación, la fricción es la no-linealidad más investigada y de la que se disponen más modelos hasta la fecha. Quizás, una de las razones es que, desde el punto de vista de los sistemas de control, es un fenómeno sobre el que se pueden alcanzar mejorías notables en las prestaciones de los servosistemas fruto de las compensaciones.

La idea principal es que para poder vencer los errores de posicionamiento y de seguimiento de trayectoria, es imprescindible compensar la fuerza de fricción, para lo cual se hace necesario modelarla. Varios autores parten de un concepto básico que sirve como punto de partida, enfocando inicialmente el problema desde el punto de vista estático.

El modelo de fricción más elemental es el llamado modelo de Coulomb, en el que la fricción se opone al movimiento pero se asume que la magnitud de la fricción es constante. Este modelo permitió mejorar el desempeño de sistemas pero no resolvió todas las dificultades ocasionadas por la fuerza de fricción. Por ello, se introdujo un modelo que considerara la fricción viscosa, dado por:

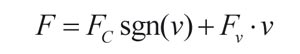
donde F representa la fuerza de fricción, FC representa el nivel de fricción de Coulomb, v representa la velocidad relativa entre las dos superficies, sgn() representa la función signo y Fv representa el coeficiente de fricción viscosa.

Posteriormente, este modelo se completa teniendo en cuenta que existe una fuerza de fricción en reposo, denominada fuerza de fricción estática o fuerza de desprendimiento (Fs). Se establece que una fuerza de fricción en reposo es mayor en magnitud a la fuerza de fricción de Coulomb. Sin embargo, las fuerzas externas contrarrestan a la fricción estática bajo un cierto nivel para poder así mantener un objeto en movimiento. Por tanto, la fricción en reposo no puede ser descrita como una fuerza en función de la velocidad, sino que debe ser modelada usando fuerzas externas (Fe).

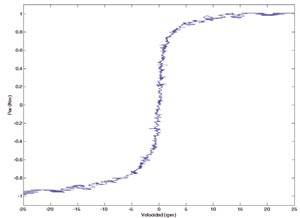
Todas estas aproximaciones contienen componentes que son lineales en velocidad. Sin embargo, Richard Stribeck observó que la fuerza de fricción no se comporta como en los anteriores modelos, sino que demuestra que la fuerza depende de la velocidad. El fenómeno anterior es el llamado efecto Stribeck.

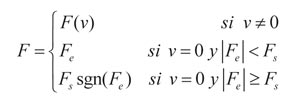
donde F(v) es una función arbitraria. Aunque esta función ha sido parametrizada por varios autores, una forma bastante extendida de representar esta no linealidad es la propuesta en (3):

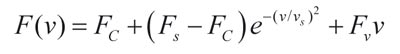
donde FC es el nivel de Fricción de Coulomb, Fs es el nivel de fuerza de desprendimiento y vs es la velocidad de Stribeck.

La principal desventaja cuando se usa un modelo como el de la ecuación (3) para simulaciones o propósitos de compensación está en que posee una discontinuidad en v = 0 y, por tanto, resulta demasiado idealista. Se ha comprobado que el modelo de fricción discontinua es una simplificación no-física, en el sentido de que el contacto mecánico entre la masa distribuida y la superficie de contacto no puede exhibir un cambio instantáneo en la fuerza [8]. A partir de ahí, se han desarrollado numerosos modelos de fricción sin discontinuidad, entre los cuales destaca el modelo de Karnopp. En él, la discontinuidad se elimina mediante la introducción de una región muy pequeña (finita) en la zona de velocidad cero, en la que la fuerza de fricción se supone linealmente proporcional a la velocidad hasta un determinado umbral de velocidad (vth).

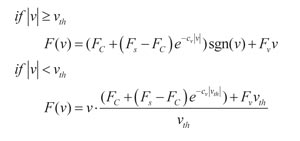
A diferencia de la ecuación (3), en este modelo se reemplaza la denominada velocidad de Stribeck (vs) por un coeficiente cv de naturaleza similar ya que representa la transición entre la fricción estática y la de Coulomb.

Tratando también de reproducir alguna de las dinámicas complejas de la fricción, se desarrolló el conocido como modelo de Armstrong. Este modelo introduce dependencias temporales para la fricción estática y para el efecto Stribeck, pero no trata los efectos que aparecen en el predeslizamiento. Existen en la literatura otra serie de modelos de fricción estáticos como son el modelo de Tustin o el modelo de Lorentzian, entre otros, que no serán tratados en este artículo bien porque no son utilizados para la compensación de la fricción debido a su complejidad computacional y ajuste experimental, o bien porque son casos particulares del efecto Stribeck [8].

Aunque todos los modelos anteriores contribuyeron al diseño de controladores que lograron disminuir los efectos de la fricción, no pudieron eliminarlos por completo al no representar ciertos comportamientos dinámicos. Esto condujo a la aparición de nuevos modelos (dinámicos) con la finalidad de reproducir los efectos más complejos de la fricción y enfrentar los nuevos retos que a su vez trajo consigo la reducción de los efectos más notorios de la fricción y el efecto de otras no linealidades de menor amplitud. No obstante, estos modelos estáticos siguen siendo ampliamente utilizados para el diseño de sistemas de compensación.

Desde el punto de vista dinámico, uno de los modelos utilizados para representar las dinámicas de los efectos más complejos de la fricción es el modelo de Dahl [9]. Este modelo dinámico de fricción es uno de los más sencillos y se basa en la deformación de las asperezas de las superficies de los cuerpos en contacto. Es capaz de considerar el pre-deslizamiento y su desplazamiento permanente. Para la región de deslizamiento el modelo tiende a la fricción de Coulomb, por tanto, no contempla algunos fenómenos que ocurren a bajas velocidades (no capta el efecto Stribeck ni, por tanto el fenómeno stick-slip). Debido a ello, una vez que el par aplicado supera la fricción de Coulomb, el deslizamiento se inicia con una aceleración constante y se presentan errores en el control de movimiento y posicionamiento. El modelo de Dahl en conjunto con la fricción viscosa es el siguiente:

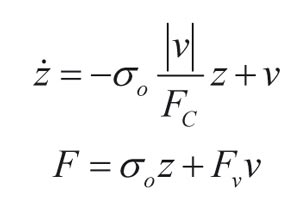
donde F es la fricción, σo es el coeficiente de rigidez de las cerdas, v es la velocidad, Fv es el coeficiente de fricción viscosa y FC es la fricción de Coulomb.

Una modificación del modelo anterior es el Modelo de LuGre [10], que es uno de los modelos más difundidos en la actualidad. El modelo de LuGre está basado en la suposición de que, a nivel microscópico, las imperfecciones de las superficies de contacto presentan hebras elásticas que causan los efectos de fricción. El modelo de LuGre está definido por la siguiente ecuación:

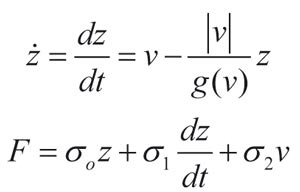
donde z es el estado interno y no medible del modelo que representa la deflexión media de las hebras, σo es el coeficiente de rigidez, σ1 es el coeficiente de amortiguamiento, σ2 es el coeficiente de fricción viscosa y g(v) representa la función que describe el efecto Stribeck.

En los últimos años también se ha trabajado con el modelo dinámico GMS (Generalized Maxwell Slip), que representa una nueva formulación aproximada del modelo de deslizamiento de Maxwell con variables de estado [11]. En resumen está basado en el modelo de LuGre en combinación con un modelo denominado de Leuven. En la literatura hay reportados más modelos dinámicos como el modelo de cerdas (Bristle model), el modelo integrador de reajuste (Reset Integrator model) o el modelo de Bliman y Sorine [10].

Los modelos dinámicos hasta aquí descritos son muy útiles para reproducir el comportamiento de la fricción pero resultan poco prácticos para el diseño de modelos/compensadores ya que, o no representan todos los efectos a la perfección, o si lo hacen requerirían de múltiples estimaciones para compensar una fuerza. De ahí que muchos autores compensen la fricción con un modelo simplificado como el modelo de Coulomb o el de Karnopp. Lógicamente, la idea no es compensar únicamente el componente estático, sino tomar este componente como base para un compensador adaptivo que pueda hacer frente a los efectos complejos de la fricción.

2.2 Holgura

A la hora de modelar la holgura, es necesario conocer que se compone de dos características: histéresis mecánica y fenómeno de impacto entre dos superficies relativamente duras que entran en contacto. Al contrario que la fricción, la holgura o backlash es un fenómeno que se encuentra bastante bien definido y entendido, y puede ser abordado con distintos grados de detalle, ya sea como una simple banda muerta o como una banda muerta con dinámicas de impacto, usando la teoría de la mecánica establecida.

El modelo clásico toma la visión más simple de la holgura utilizando sencillamente una banda muerta centrada alrededor de un punto de equilibrio desplazado. Este modelo no toma en cuenta la dinámica transitoria del impacto e, implícitamente, considera todos los impactos como si los elementos fueran completamente plásticos. Pese a ser un modelo que no toma en cuenta el régimen transitorio, ha sido un modelo ampliamente utilizado en multitud de compensaciones hasta no hace mucho tiempo. Las razones predominantes para esta simplificación son de dos tipos: en primer lugar, las grandes máquinas industriales (con tolerancias relativamente grandes) en su funcionamiento en régimen estacionario no sufrían, por lo general, cambios de dirección en sus operaciones habituales. En segundo lugar, las máquinas más pequeñas (tales como, por ejemplo, los famosos relojes de bolsillo suizos) tenían engranajes muy pequeños casi sin masa y, por tanto, prácticamente no se transfería energía de impacto a otros engranajes. En resumen, no fue originalmente una necesidad apremiante el modelar la dinámica de impacto, así como tampoco era un problema muy conocido en el momento.

El modelo de holgura clásico se ha utilizado ampliamente en teoría de control, y el fenómeno de impacto también ha recibido mucha atención por parte de la comunidad científica afín a la robótica. Sin embargo, no son muchos los modelos que combinan el impacto y la holgura como tal en el modelado y control de servomecanismos, sino que es más habitual combinar modelos de fricción y holgura (sin impacto). Para más detalles se recomienda consultar la tesis doctoral [12].

Las máquinas modernas requieren mayor precisión que las de hace un siglo, y las tolerancias más estrictas en sus mecanismos son un desafío permanente a la tecnología de la máquina. Ambos aspectos dinámicos del backlash (banda muerta e impacto) han tenido, con el paso del tiempo, un mayor peso en cuanto a fenómenos significativos conducentes a la imprecisión de la máquina. Un modelo de backlash completo debe incluir la rigidez y la dinámica cuasi-elástica del impacto en conjunción con la banda o zona muerta.

Existen otra serie de modelos de holgura en la literatura a parte del modelo clásico de zona muerta o el modelo más moderno que incluye dinámicas de impacto. El trabajo [13] muestra un conjunto bastante amplio de modelos de holgura utilizados para el control de sistemas mecánicos con backlash. El reporte técnico [14] también resume y comparte varios de los modelos existentes. De entre los distintos modelos, destaca el modelo de histéresis. El modelo de histéresis relaciona el ángulo de salida del backlash θl, con el ángulo de entrada θm bajo el supuesto de que se trabaja con un eje rígido. Sin embargo, bajo esta misma premisa existen distintas representaciones de esta histéresis.

También existen otra serie de modelos que a través de funciones descriptivas, funciones en espacio de estados (definidas en algún trabajo como modelos exactos o en otros como modelos de impacto), modelos físicos, etc., representan el fenómeno con distintos grados de complejidad. Lo cierto es que desde el punto de vista de su aplicación, el más extendido es el modelo clásico desechándose, en cierta medida, estos últimos modelos en base a su complejidad.

Dentro de los distintos métodos que se utilizan para, por ejemplo, compensar la fricción en servomecanismos se pueden encontrar técnicas de compensación no basadas en modelo (stiff PD control, integral control with deadband, joint torque control, impulsive control, dither, etc), técnicas de control basadas en modelo (adaptive control, friction model feedforward/feedback, etc), técnicas basadas en inteligencia artificial, etc. [8].

Sin embargo, al igual que una gran cantidad de aplicaciones industriales, todas estas técnicas de compensación se encuentran sobre la base de sistemas de control en cascada para el control de la posición, velocidad, trayectoria, etc. Como bien es sabido, el control en cascada consiste en incluir uno o más lazos de control interno dentro de otro externo, con el objetivo de anular perturbaciones, impidiendo que estas perturbaciones secundarias afecten al sistema principal. Básicamente el controlador externo se encarga de la variable principal, mientras que los controladores internos se encargan de las perturbaciones más frecuentes. Como principales ventajas de este sistema de control es que las perturbaciones más frecuentes son corregidas antes de afectar a la variable principal, además de que se permiten usar ganancias altas, obteniendo una rápida respuesta

La idea en este trabajo es, en vez de utilizar sofisticadas técnicas de compensación de no linealidades como las existentes en la literatura, optimizar los parámetros de control de un sistema de control de posición básico como es el control en cascada (que además es uno de los más utilizados) para tratar de compensar las no linealidades. El hecho de utilizar un control simple en cascada permitirá sacarle un mayor partido a las técnicas de optimización de parámetros y ver, más aún si cabe, el potencial que brinda esta serie de técnicas.

El lazo de control en cascada utilizado en este trabajo constará de dos niveles y se utilizará para el control de posición del motor que gobierna uno de los ejes en una supuesta máquina herramienta de 3 ejes. En este sistema de control se utilizará un control PI en el bajo nivel para controlar la velocidad y un control P en el nivel más alto para el control de posición. Los órdenes de respuesta en el control de servomecanismos de este tipo don del orden de decenas de microsegundos. Por la necesidad de una rápida respuesta computacional y al tratarse de una aplicación industria, es común el empleo de controladores P, PI o PID por su sencillez, rápida respuesta y extenso conocimiento a nivel personal del técnico.

En este tipo de sistemas, pueden darse ciertos comportamientos dinámicos en el régimen transitorio y en el permanente. Por ello, se decide incluir en el lazo de control una acción anticipativa, consistente en obtener la velocidad a partir de la variable de entrada (posición) para actual simultáneamente sobre la variable manipulada del lazo externo. Así, se consigue un ajuste adecuado para la compensación de los comportamientos dinámicos a través del control, encargándose la acción anticipativa de eliminar los errores de seguimiento y/o trayectoria a velocidades constantes.

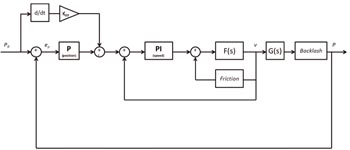
Una vez definida la estructura de control, se debe modelar el conjunto ‘plata + no linealidades’. Se trata de utilizar modelos lo más similares posibles a la realidad para poder diseñar posteriormente un procedimiento de ajuste a través de técnicas de optimización de los sistemas de control de posición, velocidad y trayectoria utilizable por empresas desarrolladoras de sistemas de control.

Como modelo de la planta se ha decidido utilizar un modelo comúnmente empleado en el ajuste de lazos de control por parte de las empresas desarrolladoras de CNC. Este modelo utiliza como parámetros la frecuencia de resonancia (w) obtenida de un procedimiento de respuesta en frecuencia del sistema, así como el amortiguamiento (ξ) y las inercias del motor y de la carga (Jm+Jl). Este modelo se divide a su vez en dos funciones de transferencia, la primera de ellas representa la relación más básica existente entre corriente y velocidad del motor, mientras que la segunda representa la función de transferencia entre la velocidad del motor y la velocidad de la carga.

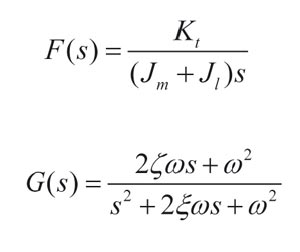
Respecto a las no-linealidades, se decide modelar la fricción en base al modelo de Karnopp (4), debido a que según pruebas experimentales es el que mejor representa el comportamiento real además de poseer una buena eficiencia computacional. Con respecto a la holgura, se decide emplear el modelo clásico de zona muerta centrado alrededor de un punto de equilibrio por los mismos motivos.

A través de este sistema de control y del modelizado de todos sus componentes se trata de desarrollar un entorno en el que se puedan realizar simulaciones lo más fielmente posibles a la realidad de los servomecanismos para poder llevar a cabo la optimización de los parámetros de control.

Cuando hablamos de optimización en el presente trabajo, de lo que es trata es de minimizar un criterio de desempeño de naturaleza funcional que evalúe el comportamiento a lo largo de un intervalo de control seleccionado a través de las señales de error, y en ocasiones de la energía de control utilizada, que resultan de controlar el proceso, sea ante una variación en los valores de referencia para las variables controladas o perturbaciones en algunas de las variables de carga.

Este problema, si bien comparte algunas características similares con el problema más general de Control Óptimo (por ejemplo el carácter funcional del objetivo a minimizar y la necesidad de satisfacer, según las restricciones, las ecuaciones que rigen el comportamiento dinámico del proceso controlado) es un problema de jerarquía inferior. La razón es que en él no se pretende obtener la política de control óptimo. Es decir, las incógnitas del problema no son las leyes de control, ni tampoco lo es la estructura del controlador óptimo, en el caso de que la solución del problema sea factible de obtener bajo la forma de ley de control en cadena cerrada. En el problema de ajuste de un controlador mediante la técnica de optimización paramétrica, la estructura del controlador es seleccionada de antemano y las incógnitas pasan a ser un número finito de parámetros definidos sobre la estructura del controlador (las ganancias de los controladores P y PI en nuestro caso), cuyos valores vienen a ser lo que se conoce comúnmente como los ajustes del controlador.

En este trabajo, para dicha optimización de parámetros, utilizaremos el algoritmo de Nelder-Mead. Publicado en 1965 por Nelder y Mead [5], es un método numérico para minimizar una función objetivo en un espacio multidimensional. La aplicación del algoritmo básico es relativamente fácil, además de su comprensión, por lo que su utilización ha resultado muy popular en muchos campos de la ciencia y la tecnología. El método no utiliza información sobre el gradiente de los datos, por lo que resulta adecuado para ser aplicado en problemas con funciones discontinuas o con derivadas abruptas y se enmarca dentro de la clase de métodos de búsqueda directa [15].

En el método se utiliza el concepto de un símplex, que es una forma geométrica de envolvente convexa y N+1 vértices, correspondiéndose N con el número de parámetros a optimizar. El paso básico del método consiste en sustituir el peor punto del símplex con otro punto reflejado en el resto de puntos [16].

A partir de estas condiciones iniciales, el método realiza una secuencia de transformaciones en el símplex S definido, encaminadas en reducir el valor que toma la función evaluada para cada vértice. En cada paso, la transformación está determinada por el cálculo de uno o más puntos de prueba, junto al valor correspondiente de la función para estos puntos, y se compara estos valores de la función con los correspondientes a los vértices. El proceso culmina cuando el símplex S es lo suficientemente pequeño según cierto criterio de evaluación.

El procedimiento de optimización concluye teniendo en cuenta tres condiciones diferentes:

1. Se ha alcanzado la tolerancia permitida para los datos de entrada, es decir, el símplex S resulta muy pequeño y por tanto las distancias entre sus vértices, se encuentran por debajo del nivel de tolerancia.
2. Se ha alcanzado el nivel de tolerancia preconcebido para la función f en cualquiera de los vértices del actual símplex.
3. No se ha logrado una convergencia y por tanto se alcanza un máximo número de iteraciones predeterminadas.

Entre las ventajas principales que ofrece el algoritmo de Nelder-Mead, además de ser fácil de entender y aplicar, el método permite obtener un resultado del problema a optimizar, con un número relativamente pequeño de evaluaciones de la función objetivo en cada iteración [17,18,19]. Por otro lado, su principal desventaja está relacionada con la convergencia y la influencia de las condiciones iniciales, ya que el método puede ejecutar una gran cantidad de repeticiones sin una mejora significativa en la función objetivo, a pesar de estar lejos de un valor mínimo.

4.1 Optimización de los parámetros del servomecanismo

La idea principal del presente trabajo se ha desarrollado bajo la hipótesis de que si se tienen razonablemente bien modeladas las no-linealidades, es posible realizar un ajuste óptimo de los controladores para unas condiciones determinadas. Lógicamente se trata de que no solo sean controladores óptimos para un caso concreto, sino que los parámetros del controlador optimizados reduzcan a su vez los errores para el resto de condiciones.

Considerando que los controladores en lazo de control en cascada P-PI se definen mediante leyes de control que relacionan su variable de entrada (el error e) con la acción de control u, y siendo v un vector de parámetros, ésta se puede expresar en el dominio temporal de la siguiente forma:

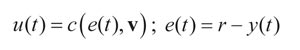
Definiendo cierto intervalo de tiempo [t0, tF] correspondiente a la respuesta temporal del sistema de control, ante cambios en la perturbación YZ o la referencia r. Por lo general, la ley de control se diseña para ciertos objetivos de control, como pueden ser: por ejemplo, que durante el intervalo de tiempo definido de la respuesta temporal, la salida del proceso y tenga muy poca variación respecto a la referencia, es decir e - 0 o muy pequeño en todo el intervalo. En otros casos el objetivo del control puede ser que la salida y cumpla algún modo de respuesta determinado, como por ejemplo, que no oscile alrededor de r, lo cual se traduce también en oscilaciones del error e alrededor de 0, o la amplitud de las posibles oscilaciones sean mínimas; y/o que el valor absoluto del error | e | alcance y se mantenga por debajo de cierto valor emax > 0, en un intervalo de tiempo de establecimiento TS tal que t0 +TS < tF; entre varios otros objetivos posibles.

A partir de la respuesta temporal del error e(t), en el intervalo definido [t0, tF], es posible definir cierta función de coste g que evalúe el comportamiento dinámico del sistema de control, mediante una cifra de mérito I:

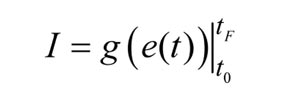
Existen varias cifras de mérito o funciones de coste, de un amplio uso en la industria en general, las cuales son empleadas tanto en la etapa de diseño como de evaluación de sistemas de control. Entre las funciones de coste de más amplia utilización está la integral del error absoluto ponderado en el tiempo (ITAE), que permite obtener una respuesta transitoria del sistema de control con un pequeño tiempo de establecimiento y sin oscilaciones (21). En específico, el criterio ITAE penaliza las respuestas transitorias de larga duración y es muy sensible ante variaciones de parámetros en comparación con otros criterios. Por otra parte, el criterio ITAE por lo general produce menores oscilaciones que otros criterios integrales cuadráticos.

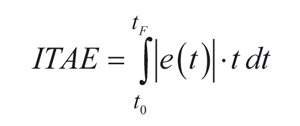
Un aspecto importante que se ha considerado es la normalización de las cifra de mérito teniendo en cuenta los valores de referencia. De este modo, se pueden comparar el criterio basado en el error independientemente de las condiciones particulares de la operación.

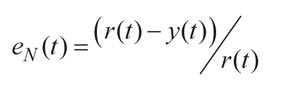
Aunque el error normalizado es de mucho interés para evaluar el desempeño bajo distintas condiciones de operación, en el caso del control de trayectorias se produce una indeterminación cuando la referencia es cero. Bajo estas circunstancias, se ha decidido establecer un umbral en la referencia (posición). Es decir, los errores se calculan siempre y cuando estemos por encima de un determinado umbral de posición. Cuando estamos en las proximidades del cero (inversión) el criterio de error se calculará utilizando como valor de referencia el propio valor umbral.

El procedimiento de optimización puede realizarse, tanto en tiempo real (on-line), es decir, empleando datos reales de r, y y u, como en tiempo de simulación (off-line), utilizando algún modelo del proceso físico y que relacione su entrada y su salida:

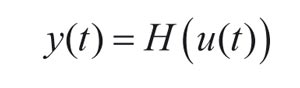
Consideremos que el procedimiento de optimización, se realice off-line, empleando el modelo del sistema + no linealidades (fricción y holgura). Consideraremos que si existiese elasticidad, ésta queda contemplada en el modelo de la planta. El cálculo de la cifra de mérito I se realiza como:

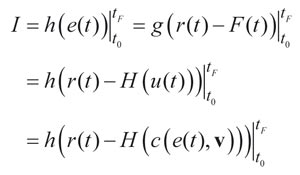
Empleando la ecuación anterior como función objetivo, y utilizando algún método de optimización, es posible minimizar la cifra de mérito I, ajustando el vector de parámetros v de la ley de control, como entrada a la función.

En el proceso de solución del problema de optimización planteado se utilizaron de forma coordinada el programa Simulink para la simulación del servosistema y el programa Matlab para la optimización de los parámetros de control. De este modo el problema queda planteado como:

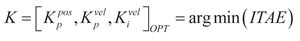
Utilizando la ecuación (15) y bajo la simulación de la realización de un círculo de Radio 50 mm a una velocidad de 5000 mm/min en el que intervienen dos ejes del servomecanismo, se han obtenido unos parámetros de control optimizados en el eje Y que ofrecen unos resultados muy positivos y prometedores tal y como se muestra a continuación.

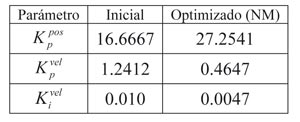
La optimización se ha llevado a cabo por la técnica de Nelder-Mead. En los algoritmos de optimización se utilizado las funciones fminsearch para la minimización sin restricciones y fmincon para las minimizaciones con restricciones. Las optimizaciones se han realizado utilizando como condiciones iniciales de los parámetros de control un ajuste habitual de los fabricantes de CNC en sus sistemas de control K=[16.66,1.2412,0.01]i. La optimalidad de las soluciones obtenidas, se verificó usándola como condición inicial de una segunda optimización. Obviamente esto puede conducir a que la solución obtenida pudiera ser sub-óptima, y no óptima globalmente, pero en cualquier caso queda demostrado en las simulaciones que son soluciones muy buenas.

Respecto a los modelos utilizados, la planta se ha correspondido a las ecuaciones (7) y (8) con una frecuencia de 30 Hz, un amortiguamiento de 0.1 y una inercia de motor + carga de 2.2•10-3 Kg/m². En cuanto al modelo de fricción se ha utilizado el modelo de Karnopp con parámetros FC = 0.625 Nm, Fs = 0.625 Nm, vth = 1•10-4 rad/s, Fv = 0.25•10-4 Nm y cv = 10. Como holgura se ha utilizado el modelo clásico para representar una holgura de 9 μm. Por otra parte, se ha utilizado ganancia unitaria para la acción anticipativa.

La idea del trabajo es que no solo sean parámetros de control óptimos para un caso concreto (radio =50mm, velocidad de avance = 5000 mm/min), sino que los parámetros del controlador optimizados reduzcan a su vez los errores para el resto de condiciones. Por ello se han probado para la misma operación de la realización de un círculo a distinta velocidad (1000 mm/min) y con otro tipo de trayectoria completamente diferente (vaivén a lo largo de un eje combinando alta y baja velocidad -60/18000 mm/min-).

La siguiente tabla muestra una disminución significativa (hasta más del 50% en algunos casos) de los errores en distintas condiciones utilizando parámetros del controlador óptimos. Para el estudio comparativo no se ha utilizado simplemente el criterio ITAE utilizado para la optimización, sino que se muestra también otra de las cifras de mérito utilizadas en la industria como es el Integral Time Square Error (ITSE).

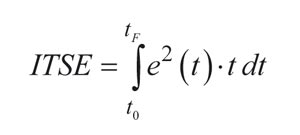
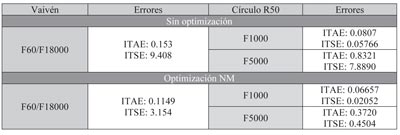
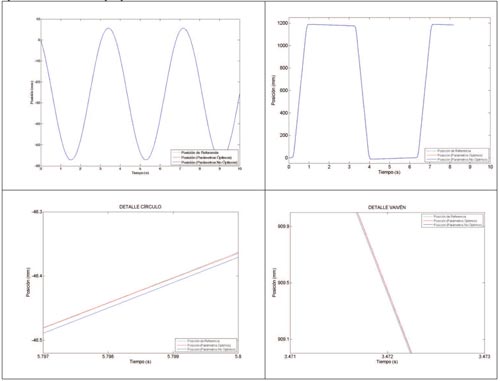
Tal y como se puede apreciar en la tabla, los parámetros optimizados presentar menor error que los parámetros no óptimos en el control de la posición. La Figura 3 muestra con un poco más de detalle el efecto que tiene los parámetros optimizados en el control de la posición del servomecanismo. Aunque aparentemente existe poca diferencia en el resultado general, a través de los detalles se aprecia como se hace un seguimiento mucho más preciso (con menor error) de la posición de referencia a lo largo del tiempo.

Posteriormente, los resultados de estas simulaciones se han confrontado con resultados obtenidos en experimentos reales, verificando así que las simulaciones representan de un modo muy aproximado la realidad.

Este trabajo se ha realizado en el marco del proyecto ‘Coindservo’: Compensación Inteligente de Nolinealidades Duras en Servosistemas” financiado por Fagor Automation S. Coop. Igualmente, los autores agradecen el proyecto CONMICRO DPI2012-35504 financiado por el Ministerio de Economía y Competitividad. Finalmente, los autores reconocen el inestimable apoyo de Fagor Automation S. Coop. a las fases de investigación y desarrollo cuyos resultados se han plasmado en este trabajo.

El presente trabajo ha explorado y evaluado una estrategia de sintonía óptima de los parámetros del sistema de control para el tratamiento de las no linealidades. La idea es tratar de desarrollar un procedimiento más simple que el que conllevaría el cálculo y diseño de sistemas de compensación de fricción y holgura. El objetivo es crear un procedimiento en base a un esquema de control sencillo como es el esquema de control en cascada con reguladores P y PI para que un operario pueda ajustar los reguladores según sus conocimientos y experiencia. A partir de este ajuste se pondría en funcionamiento el algoritmo de optimización para conseguir, a partir de unas condiciones de funcionamiento y operación determinadas, una mejora en el comportamiento global del servomecanismo.

En este trabajo de investigación hay que destacar que los resultados en simulación son muy prometedores con mejoras que llegan a más del 50% en los criterios de error analizados. No obstante, la fase actual de la investigación en esta línea nos lleva directamente a realizar pruebas en máquina para corroborar que los resultados obtenidos en simulación son válidos en condiciones reales.

Lógicamente, la optimización por sí misma sin la utilización de componentes anticipativas en el esquema de control no resolvería por completo la problemática. Por ello, es precisamente la conjunción de un esquema de control simple con un ajuste conocido, junto a la incorporación de componentes anticipativas más los procedimientos de optimización, los que propiciarían la utilidad práctica del método propuesto.

Referencias

[1] Y. Altintas, A. Verl, C. Brecher, L. Uriarte, and G. Pritschow, “Machine tool feed drives, ”CIRP Annals - Manufacturing Technology, vol. 60, pp. 779-796, 2011.

[2] R. Haber, A. Gajate, M. Novo, C. R. de Yurre, J. Zurbitu, and A. Lazkano, “Revisión y Estudio de Técnicas de Inteligencia Artificial para la Compensación de la Fricción en Sistemas Electromecánicos, ” presented at the VIII Simposio CEA de Control Inteligente, Baiona (Pontevedra), 2012.

[3] A. Bozic, J. Deur, and N. Peric, “Gain scheduling-based friction compensation”, 2000, pp. 1089-1095.

[4] I. B. Tijani, M. Wahyudi, and H. Talib, “Adaptive neuro-fuzzy inference system (ANFIS) for friction modelling and compensation in motion control system, ” International Journal of Modelling and Simulation, vol. 31, pp. 32-41, 2011.

[5] J. A. Nelder and R. Mead, “A simplex method for function minimization, ” The computer journal, vol. 7, pp. 308-313, 1965.

[6] L. Y. Kuo and J. Y. Yen, “A genetic algorithm-based parameter-tuning algorithm for multidimensional motion control of a computer numerical control machine tool, ” Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, vol. 216, pp. 429-438, 2002.

[7] A. Aggarwal and H. Singh, “Optimization of machining techniques—a retrospective and literature review, ” Sadhana, vol. 30, pp. 699-711, 2005.

[8] B. Armstrong-Hélouvry, P. Dupont, and C. C. De Wit, “A survey of models, analysis tools and compensation methods for the control of machines with friction, ” Automatica, vol. 30, pp. 1083-1138, 1994.

[9] R. Kelly and V. Santibañez, “Control de Movimiento de Robots Manipuladores, ” Pearson Education, 2003.

[10] H. Olsson, K. J. A_stro_m, C. Canudas De Wit, M. Ga_fvert, and P. Lischinsky, “Friction Models and Friction Compensation, ” European Journal of Control, vol. 4, pp. 176-195, 1998.

[11] F. Al-Bender, V. Lampaert, and J. Swevers, “The generalized Maxwell-slip model: A novel model for friction simulation and compensation, ” IEEE Transactions on Automatic Control, vol. 50, pp. 1883-1887, 2005.

[12] J. A. De Marchi, “Modeling of dynamic friction, impact backlash and elastic compliance nonlinearities in machine tools, with applications to asymmetric viscous and kinetic friction identification, ” Mechanical Engineering, Rensselaer Polytechnic Institute, Troy (New York), 1998.

[13] M. Nordin and P. O. Gutman, “Controlling mechanical systems with backlash – A survey, ” Automatica, vol. 38, pp. 1633-1649, 2002.

[14] A. Lagerberg, “A literature survey on control of automotive powertrains with backlash, ” Technical Report, vol. R013-2001, 2001.

[15] T. G. Kolda, R. M. Lewis, and V. Torczon, “Optimization by direct search: New perspectives on some classical and modern methods, ” SIAM Review, vol. 45, pp. 385-482, 2003.

[16] W. K. Hastings, “Monte carlo sampling methods using Markov chains and their applications, ” Biometrika, vol. 57, pp. 97-109, 1970.