Afinando los tiempos de mecanizado
Los sistemas CAM actuales estiman el tiempo de mecanizado considerando que la máquina se moverá de acuerdo a la velocidad de avance programada. Por lo tanto, la inexactitud de esta estimación puede alcanzar errores superiores al 1000%, lo que hace que la industria no utilice la estimación de tiempo proporcionada por el software CAM. Esta limitación dificulta todo el cronograma de producción de una industria, haciendo imposible la integración con sistemas de soporte de producción, como MRP y ERP. El presente trabajo investiga esta limitación tecnológica y presenta alternativas para predecir el tiempo real del fresado de formas complejas en máquinas CNC.
1. Introducción
Los últimos avances en los procesos de fabricación en el sector metalúrgico, como la fabricación aditiva, han permitido imprimir productos metálicos con propiedades mecánicas muy similares a las fabricadas por métodos convencionales, eliminando muchas limitaciones en la fabricación de geometrías complejas, o permitiendo la fabricación de cavidades internas. Sin embargo, el proceso de fabricación sustractiva de material todavía ocupa un espacio importante en la cadena de producción, ya sea para el acabado y el ajuste de tolerancias, o incluso para la fabricación de bajo coste donde se ajusta la producción de piezas compuestas de geometrías primitivas como cilindros y hexágonos.
Entre los procesos de fabricación con sustracción de material, el torneado y el fresado tienen mayor importancia debido a su volumen de aplicación. Entre ellos, el fresado es el más utilizado para fabricar piezas con formas más complejas, el cual se aplica en las industrias de moldes y matrices, aeronáutica y energía.
Aunque este proceso es bien conocido, predecir el tiempo de fabricación y la calidad de la superficie no es una tarea fácil, especialmente en la fabricación de productos con geometrías más complejas donde el proceso de acabado se realiza con herramientas de bola, donde el contacto entre la pieza y la herramienta cambia constantemente durante el proceso. Además, el proceso de acabado ocupa una parte importante del tiempo de fabricación y está directamente relacionado con la calidad del producto final. Como ejemplo en la industria de moldes y matrices, donde se requiere un acabado a espejo y una mejor calidad superficial, para después se reducir significativamente el tiempo de pulido.
En el proceso de producción de cualquier producto, un paso importante es la planificación del tiempo de fabricación, ya que este afecta directamente al tiempo de entrega, el costo y la planificación de la producción. Dependiendo del proceso de producción, puede tener un efecto mayor o menor. En la producción de lotes pequeños, la estimación precisa es esencial al realizar los presupuestos, y si el producto tiene dimensiones significativas, los efectos en el tiempo de producción pueden incluso comprometer la producción y las ganancias de la empresa. Mientras que, en la producción de grandes lotes, la validación experimental se puede amortizar transfiriendo el coste a todos los productos. En este caso, es más importante en la fase de elección del proceso de producción.
Desde el punto de vista actual, las empresas están tendiendo a la implementación de gemelos virtuales que representen fielmente los procesos productivos, para ello, es necesario modelar correctamente tanto las máquinas como sus comportamientos, representando de esta manera correctamente sus capacidades productivas.
2. Contextualización
2.1. Comunicación CAD/CAM – CNC y trayectorias da herramienta
La interpolación lineal es el método generalmente utilizado para representar una trayectoria de herramienta sobre una superficie compleja, que se describe mediante pequeños segmentos de líneas, utilizando solo funciones G01, de acuerdo con la norma DIN 66025. Los puntos cartesianos representan el principio y el final del segmento recto. La longitud de los segmentos rectos utilizados en el programa CNC está relacionada con la tolerancia de cálculo, definida por el usuario en el software CAM, asociada con la curvatura de la superficie [1].
En el proceso de cálculo de trayectoria, el software CAM calcula el punto de contacto del cortador (CC) y luego lo convierte en una ubicación de corte (CL). Usando la siguiente ecuación:
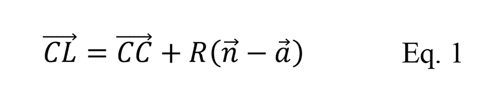
En este proceso, estos puntos que describen la trayectoria deben respetar un error máximo admitido por el usuario, para esto se utiliza un rango de tolerancia durante el proceso de cálculo. La Figura 1 muestra un esquema que representa un camino circular por segmentos lineales, esta misma analogía se puede extrapolar a cualquier superficie compleja donde el radio local cambia constantemente.
![Figura 1: Esquema de cálculo de trayectoria circular con incrementos lineales, adaptado de Souza et al. (2019)[2] Figura 1: Esquema de cálculo de trayectoria circular con incrementos lineales, adaptado de Souza et al. (2019)[2]](https://img.interempresas.net/fotos/2204592.jpeg)
Aunque es capaz de generar trayectorias de herramientas similares, los algoritmos utilizados en el software CAM para calcular las trayectorias son desarrollados por distintos proveedores de software. De esta manera, los algoritmos pueden ser diferentes. En un análisis preciso de dichos algoritmos, se puede observar que diferentes softwares calculan la ‘misma’ ruta de herramienta. Sin embargo, mirando en detalle, existen diferencias importantes en las trayectorias generadas por los diferentes programas.
Los estudios presentados en la literatura ya han demostrado que los algoritmos de cálculo utilizados por el software CAM pueden influir en todo el proceso, divergiendo entre los sistemas: tiempo para calcular la trayectoria, tiempo para postprocesar el programa NC; tamaño de los programas NC generados; disparidad en los puntos generados; lo que afecta directamente la calidad de la superficie mecanizada, y el tiempo de proceso debido a las fluctuaciones en la velocidad de avance [2].
Las máquinas tienen diferentes velocidades de procesamiento del programa CNC, ya sea debido a limitaciones mecánicas o de procesamiento, que terminan afectando la velocidad de producción. El cálculo del tiempo de respuesta de la máquina, del inglés Machine Response Time - MRT, se define como el tiempo que la máquina tarda en procesar y ejecutar el movimiento de un segmento de línea. Este concepto fue introducido por Coelho et al. (2010) [3] que presenta una metodología para el cálculo:
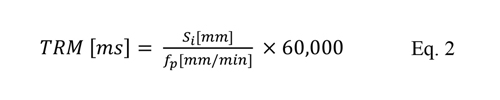
Donde Si es el tamaño del segmento, fp es la velocidad de avance observada en el numérico. Se pueden realizar variaciones en la obtención de la velocidad de avance utilizando el tiempo de ejecución del programa y conociendo la distancia total recorrida.
2.2. Rendimiento del control numérico
Los controles numéricos más avanzados permiten trabajar con amplios programas de CNC (2GB), eliminando la programación en bloque y sus inconvenientes.
Sin embargo, existen algunos factores que aún influyen en el rendimiento del CNC y, en consecuencia, limitan la velocidad de avance del mecanizado:
- Tiempo de procesamiento de bloque (TPB): es el tiempo promedio requerido para que el control numérico procese una línea de programa y envíe información para la activación de los servomotores. La longitud del segmento recto utilizado para describir una parte de la trayectoria de la herramienta (interpolación lineal de segmentos rectos), junto con el TPB, son factores que limitan el avance de mecanizado.
- Clock y Bus: la frecuencia del ‘reloj’ debe estar relacionada con el número de CPU en el sistema y la capacidad del bus. Una CPU de 32 bits tendrá un rendimiento bajo si usa un bus de 16 bits.
- Block Buffer: el CNC almacena bloques ya procesados en un área temporal (“pulmón” - Block Buffer). De esta manera, siempre hay un bloque CNC procesado esperando ser ejecutado por el servidor. Los CNC convencionales en general son capaces de almacenar hasta 10 bloques procesados. Para trabajar en altas velocidades de corte - HSC (de lo ingles High Speed Cutting), se requieren más bloques procesados en el Buffer de bloque.
Cuando la velocidad de avance programada para la es mayor que la capacidad del CNC para interpretar y enviar información de movimiento a los servomotores, existen limitaciones en el avance, que pueden causar dos situaciones diferentes, dependiendo de las características del control numérico utilizado:
- en controles obsoletos, con limitaciones de recursos: cuando la velocidad programada excede la capacidad del CNC, se producen golpes en la máquina durante el proceso de mecanizado, causando discontinuidades en el movimiento y resultando en un acabado insatisfactorio;
- en controles modernos: si ocurre la misma situación, reducirá la velocidad de avance hasta que encaje en un valor que pueda administrar [5]. Con esto, permite un acabado superficial adecuado, pero la velocidad de avance del proceso se reduce [6].
2.3. Tiempo de respuesta de una máquina CNC.
Al mecanizar formas geométricas complejas, el valor de avance pode fluctuar de manera considerable durante el mecanizado. Estas oscilaciones se deben a las limitaciones tecnológicas y dinámicas de la máquina y al equipo de control numérico (CNC). Cada equipo tiene sus características, con grandes diferencias de rendimiento entre las máquinas actuales [4].
Para identificar el rendimiento de una máquina con un CNC determinado e identificar las limitaciones de movimiento para mecanizar formas complejas, se utiliza la metodología llamada TRM - Machine Response Time. El método para obtener esta variable se presenta a continuación:
- Se desarrolla un programa CNC que contiene movimientos lineales de líneas rectas, utilizando el código G01, con pequeños incrementos, en la dirección del eje a analizar. La trayectoria debe realizar una trayectoria significativamente mayor que la distancia de un incremento a una alta velocidad programada, en el caso evaluado fue mayor a 5,000 mm/min. Debido a limitaciones tecnológicas, se sabe que incluso utilizando máquinas CNC modernas y de alta velocidad, todavía no son capaces de ejecutar este movimiento a altas velocidades de avance.
- El programa CNC debe ejecutarse en la máquina específica. Durante el movimiento de la máquina, el operador debe observar en la pantalla del CNC la velocidad de avance alcanzada a lo largo del camino - Fmax.
- El valor Fmax se usará en la ecuación 2 para obtener el TRM.
Con la variación del tamaño del segmento es posible obtener el perfil de respuesta de la máquina y predecir su comportamiento de acuerdo con la tolerancia aplicada en la generación del programa.
Esta metodología utilizada ya ha demostrado ser bastante eficiente para predecir el tiempo de los programas que usan 3 ejes. Este trabajo contribuye al estudio de máquinas multieje que buscan entender la relación de los ejes lineales y angulares. De esta forma, se investiga el pronóstico del tiempo de mecanizado con 4 y 5 ejes donde el error de pronóstico puede ser mayor al 1000%.
3. Procedimiento experimental
Para evaluar los errores de cálculo predichos por el conjunto de control de máquina CNC, se han evaluado dos máquinas de 5 ejes con ejes rotativos A y C, una Hermle C 62 U MT con control Siemens 840D y una Ibarmia ZV25 U600 con control Heidenhain 530i.
Al utilizar geometrías de forma libre que requieren movimiento de al menos 4 ejes para el acabado, se espera que los errores en relación con el tiempo de mecanizado real sean mayores. Posteriormente, el tiempo predicho por el programa CAM (con una tolerancia de una décima y una centésima) se comparó con el calculado por el simulador CNC y el tiempo real de mecanizado de la máquina. Durante el mecanizado, se utilizó el 100% de la rotación del husillo y el movimiento vacío, simulando el mecanizado con el 100% de avance.
Durante el proceso experimental, se deshabilitaron todas las funciones de suavizado de trayectoria para verificar el valor de movimiento real del conjunto de los controles numéricos de las máquinas. Además, no se usó la función ‘tool-tip’, que no permite la inversión cinemática en programas de varios ejes.
Después de verificar que la magnitud de los errores de pronóstico tanto en el software CAM como en el simulador interno de la máquina eran grandes, la metodología de Coelho et al. (2010), que se desarrolló para el movimiento lineal (3 ejes), fue aplicada para intentar reducir los errores relacionados con la estimación del tiempo de mecanizado.
Se utilizó la misma metodología de ejes lineales para los ejes angulares. En el análisis, se descubrió que para la cinemática angular el tamaño del seguimiento formado es irrelevante para el procesamiento, aunque se pueda relacionar entre sí, la limitación está en la reducción del incremento angular.
Los ejes lineal y rotativo se evaluaron primero de forma independiente. Para obtener los parámetros iniciales del segmento de la matriz experimental, se crearon programas que reducen el tamaño del segmento (lineal o angular) hasta que se encuentre una reducción en el avance. Los valores de los incrementos y las distancias cubiertas para la evaluación se muestran en la tabla 1.
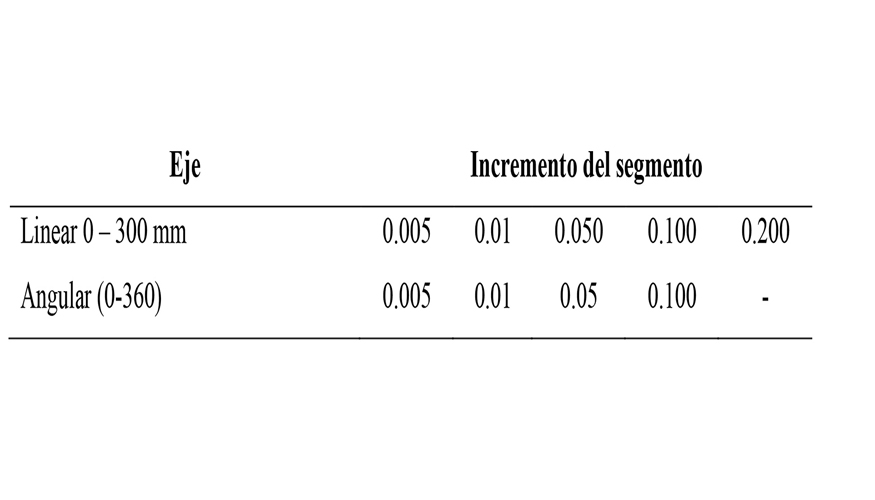
Después de pruebas individuales de cada eje rotativo, se realizaron combinaciones de ejes y se encontró que para las máquinas evaluadas:
- Cada eje lineal tiene control de movimiento independiente, con la longitud de ruta más larga siempre determinando el tiempo de segmento más largo.
- Los ejes angulares son más lentos que los ejes lineales y el primero tiene dominio al mezclar el tiempo de respuesta de los segmentos con el movimiento mixto.
Con las pruebas individuales se ha realizado una metodología en la que se ha propuesto la elección entre el tiempo de cada seguimiento considerando movimiento angular y lineal. La metodología fue aplicada a programas de 4 ejes para las 2 geometrías.
4. Resultados y discusiones
Las trayectorias mostradas en la figura 2 muestran que el tiempo de ejecución de programas con tolerancias de una décima de milímetro y una centésima presentan errores significativos incluso para el simulador interno del control numérico Heidenhain 530i.
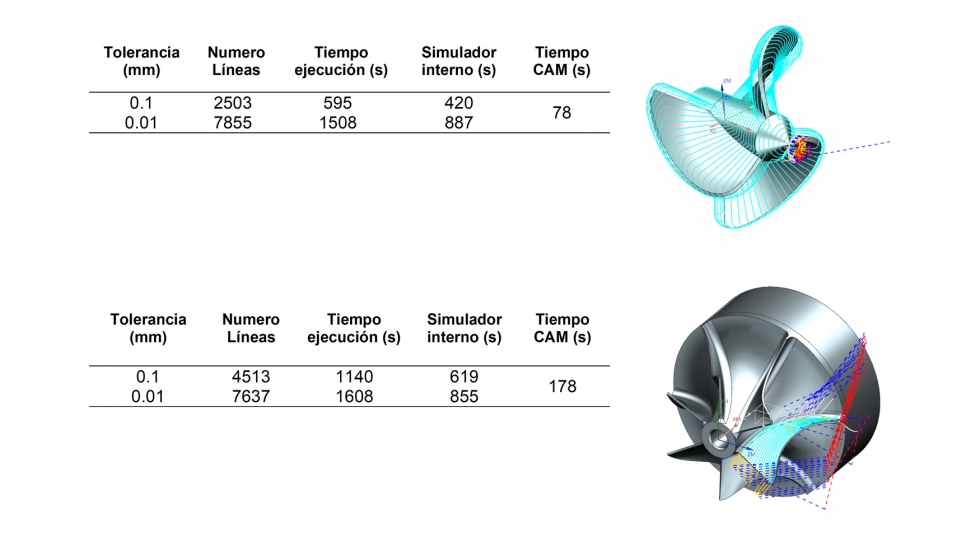
Considerando a menor tolerancia (caso critico), se encontró que para la geometría 1 - hélice, el error en relación con el simulador fue 1833% y CAM con 1037%. Para la geometría 2 - rotor, el error en relación con el simulador fue 803% y en relación al CAM 380%. Las respuestas para cada eje, lineal y angular, se muestran en la figura 3.
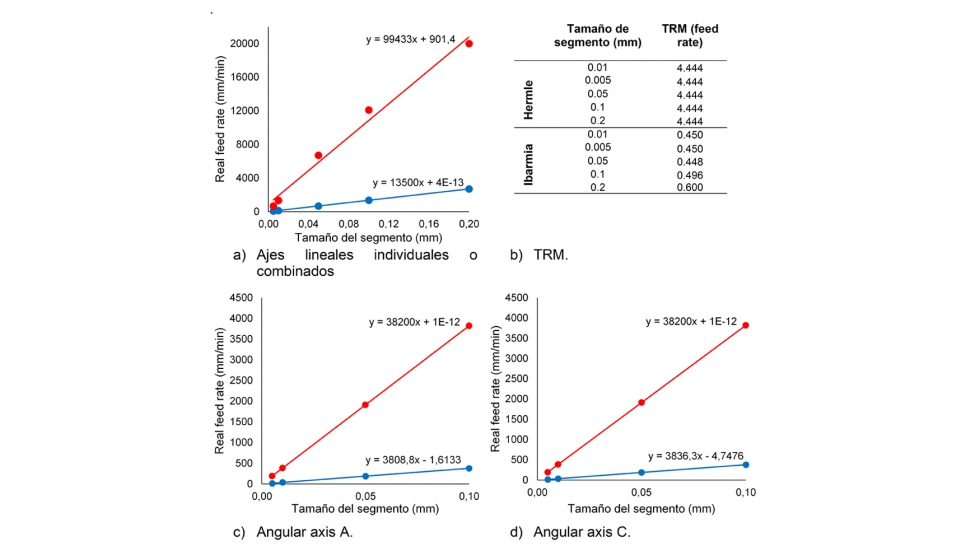
Todos los ejes evaluados individualmente de las máquinas CNC mostraron resultados con un patrón de respuesta lineal. Si no se exceden los límites mecánicos de los ejes de la máquina, la limitación del control es el principal componente limitante del rendimiento durante el proceso de fresado.
Analizando los resultados presentados en la figura 3, primero se puede concluir que el centro de mecanizado Ibarmia con control numérico Heidenhain 530i es mucho más rápido que el centro Hermle con control Siemens 840 en aproximadamente 10 veces. La figura 4 muestra la comparación del tiempo de respuesta de las dos máquinas.
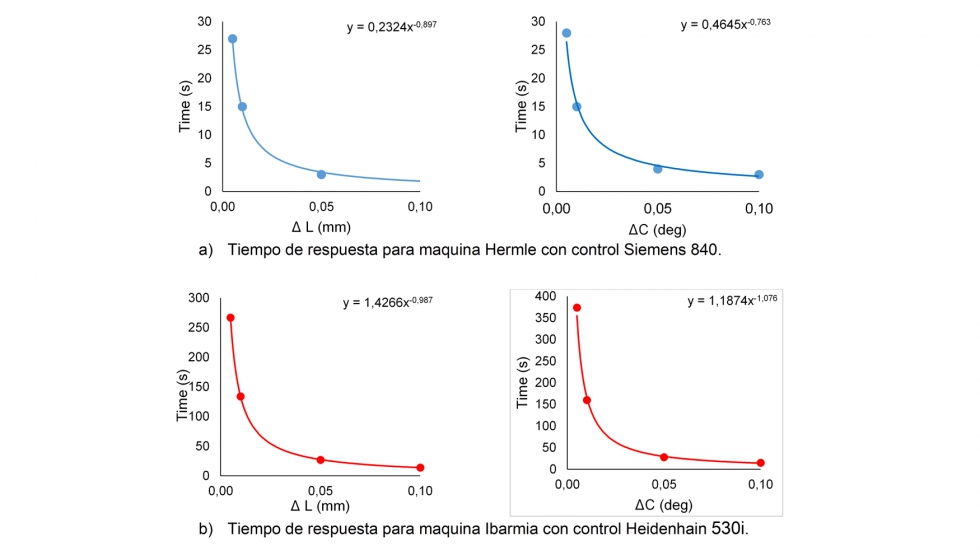
Parece que el conjunto de máquinas CNC de las dos máquinas evaluadas tiene diferentes tiempos de respuesta, en ambos casos el patrón tiene un carácter exponencial y la reducción del tamaño del segmento afecta exponencialmente el tiempo de ejecución del programa.
Se sabe que la tolerancia afecta la calidad de la superficie y, si es posible, dejarla lo más alta posible dentro de sus especificaciones puede generar ganancias significativas para la producción a gran escala.
Para mejorar el presupuesto es necesario realizar un tratamiento en el programa CNC a fin de reducir la estimación en el tiempo de mecanizado. Para ello, se expone la siguiente metodología:
1. Identificar los movimientos lineales y angulares de cada línea del programa CNC (refiriéndose a un incremento lineal o de arco)
2. La elección del tiempo de seguimiento es siempre por el incremento más pequeño, ya que es el límite.
3. Como el movimiento angular es más lento que el lineal, si se usa como referencia para calcular el arco hasta un cierto valor donde la reducción en el tamaño del segmento lineal se vuelve dominante. Se requieren condiciones de elección para cada máquina con el fin de comparar si el dominio lineal o angular se utiliza en el cálculo de acuerdo con los incrementos.
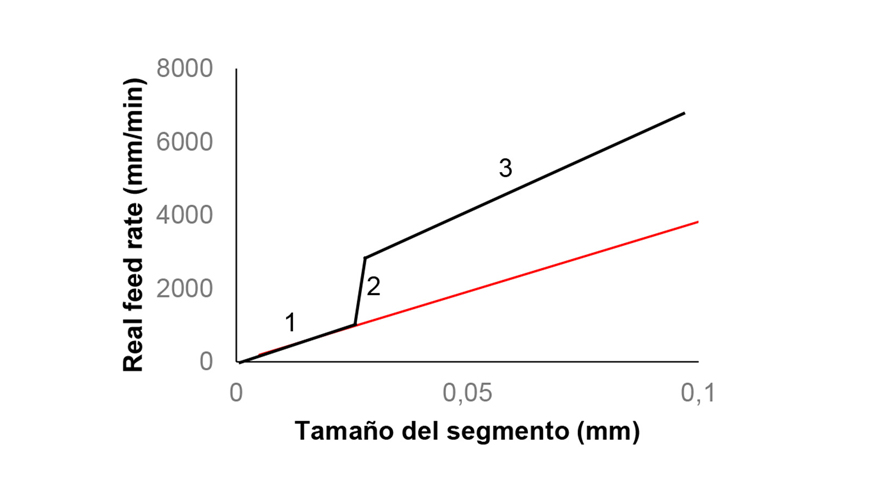
4. Agregar los tiempos de cada línea del programa CNC para calcular cada segmento y obtener el tiempo de mecanizado total por la suma.
Para evaluación del método utilizado fue realizada una nueva programación, en 4 ejes, utilizando las geometrías 1 y 2. La Tabla 2 presenta la comparación entre los errores obtenidos en relación con el CAM y la estimación utilizando la metodología propuesta.
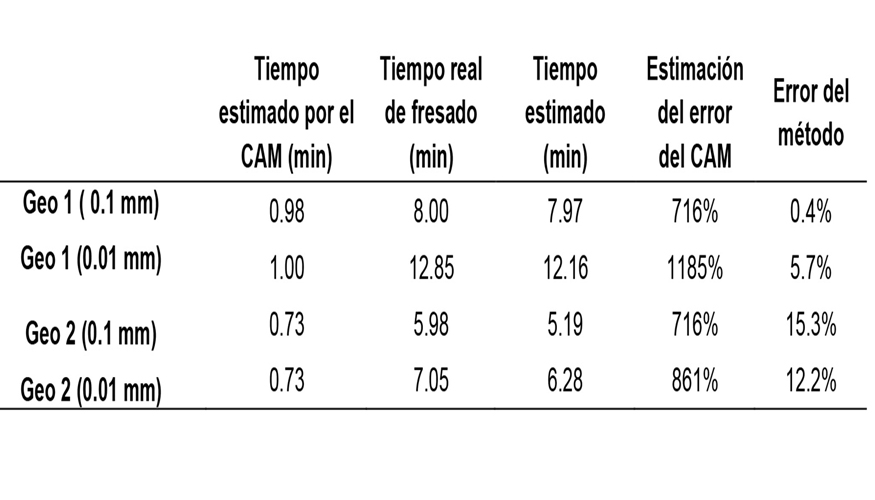
Los resultados expuestos en la tabla 2 muestran que para una tolerancia de 1 centésima de milímetro se pueden llegar a alcanzar errores superiores al 1000%. Mientras que, si se tratan los valores del programa CNC, es posible mejorar la estimación, obteniendo así unos valores razonables, siendo estos inferiores al 10%, lo cual es muy importante a la hora de presupuestar un proyecto.
5. Conclusiones
Las principales conclusiones que se han obtenido de este trabajo se indican a continuación:
- Modelo propuesto por Coelho et al. (2010) debe usarse para predecir el movimiento lineal de la máquina y su tiempo de respuesta no funciona para los ejes angulares.
- Entre las máquinas evaluadas, el Ibarmia ZV25 U600 con control Heidenhain 530i se mostró más rápida que la Hermle C 62 U MT con control Siemens 840D, sin embargo, la calidad de la superficie fabricada por ambos aún debe ser evaluada.
- Las pruebas realizadas mostraron que el movimiento simultáneo de un eje lineal más un angular tiene el tiempo más lento (es decir, los angulares), de esa manera el eje rápido necesita reducir la velocidad para mantener la trayectoria.
- La respuesta de los ejes angulares es inferior al de los dos ejes lineales. De este modo se hace necesario calcular el tiempo promedio del segmento en fresado de 4 y 5 ejes.
- Se observó que el tiempo de procesamiento para cada eje de las máquinas evaluadas es independiente, por lo que el tiempo total para cada segmento está limitado por el incremento más pequeño.
- Se propone para futuros trabajos investigar el retraso de la activación de los ejes que puede ser significativo para los ejes rotativos.
Agradecimientos
Los autores quieren agradecer a la agencia de desarrollo CNPq (Brasil), al laboratorio GPCAM de la Universidad Federal de Santa Catarina (UFSC) y al Centro de Fabricación Avanzada Aeronáutica - UPV/EHU.
Referencias
[1] Souza AF, Coelho RT, Rodrigues AR (2010) Manufacturing complex geometries using high-speed cutting technology. VDM Verlag. p. 130.
[2] Souza, A. F., Käsemodel, R. B., Arias, M., Marin, F., & Rodrigues, A. R. (2019). Study of tool paths calculated by different commercial CAM systems and influences on the real machining time and surface roughness for milling free-form geometries. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 41(9), 363.
[3] Coelho, R. T., de Souza, A. F., Roger, A. R., Rigatti, A. M. Y., & de Lima Ribeiro, A. A. (2010). Mechanistic approach to predict real machining time for milling free-form geometries applying high feed rate. The International Journal of Advanced Manufacturing Technology, 46(9-12), 1103-1111.
[4] Souza, A. F., & Coelho, R. T. (2007). Experimental investigation of feed rate limitations on high speed milling aimed at industrial applications. The International Journal of Advanced Manufacturing Technology, 32(11-12), 1104-1114.
[5] Pessoles, X., Landon, Y., & Rubio, W. (2010). Kinematic modelling of a 3-axis NC machine tool in linear and circular interpolation. The International Journal of Advanced Manufacturing Technology, 47(5-8), 639-655.
[6] Yong, T., & Narayanaswami, R. (2003). A parametric interpolator with confined chord errors, acceleration and deceleration for NC machining. Computer-Aided Design, 35(13), 1249-1259.