Robots manipuladores redundantes para el prototipado de grandes dimensiones
22 de junio de 2009
Las técnicas de mecanizado con robots cobran sentido en ciertas aplicaciones debido al menor coste de los robots manipuladores en comparación con máquinas herramientas específicas. De hecho, la introducción de brazos robot en los procesos de fabricación ha facilitado el trabajo de mecanizado con grandes volúmenes debido a su gran movilidad y rapidez en la ejecución de movimientos. Además, las tareas tediosas o peligrosas también les pueden ser delegadas. Un manipulador redundante es, en pocas palabras, todo aquel equipo robotizado posee más articulaciones de las estrictamente imprescindibles para alcanzar una posición en el espacio con la herramienta que sostiene en su extremo libre. El empleo de células robotizadas cinemáticamente redundantes en labores de mecanizado es cada vez mayor debido a su capacidad para evitar configuraciones singulares. Sin embargo, su uso implica una elección entre el conjunto de configuraciones posibles.
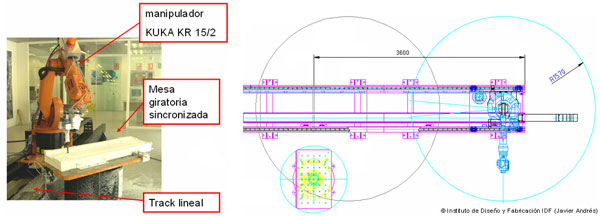
En el Instituto de Diseño y Fabricación de la Universidad Politécnica de Valencia, la plataforma NX (Siemens Corp.) está siendo empleada como entorno abierto para el desarrollo de aplicaciones Cad/Cam. Conjuntamente, las aplicaciones de la robótica en la industria del mecanizado están siendo estudiadas por medio de una célula robotizada formada por un robot manipulador Kuka KR15/2 montado en un track lineal y sincronizado con una mesa giratoria en donde se llevan a cabo las operaciones de mecanizado (Fig. 1).
Casos prácticos de aplicación
El mecanizado con robots goza de grandes expectativas en aplicaciones de prototipado y mecanizado con materiales blandos de grandes volúmenes, área antes propia de maquinas herramienta con un alto grado de especificidad. Esta transición puede ser apreciada en sendos mecanizados de prototipos de gran tamaño en espuma de poliestireno expandido (EPS), expuestos a continuación, llevados a cabo en las instalaciones del IDF-UPV.
- En el primer trabajo, se mecanizó un modelo orográfico de 8x13 metros de un embalse en el río Mijares, con ánimo de simular y estudiar las avenidas de agua y las ondas generadas cuando éstas colisionan con el agua almacenada en el embalse.
- En el segundo trabajo, se afrontó la aplicabilidad de la integración Cam/Robótica en procesos tradicionales, siendo parte de un proyecto con el Comité de Artistas Falleros de Valencia.
Varias son las ventajas encontradas en el modelado con EPS: es un material barato, fácil y rápido de mecanizar, estable en el tiempo, menos propenso a daños que otros materiales. Si es necesario, es fácilmente divisible en secciones de cara a su transporte o modificación. Además, el EPS puede ser acabado con multitud de recubrimientos superficiales que proporcionen un mayor realismo, como resinas epoxi o pinturas sin disolventes. A su vez, y en contraste con otras espumas como las de poliuretano, se ha encontrado que la salubridad es mayor dado que las virutas son de mayor tamaño, es menor su dispersión y mas fácil su aspiración.
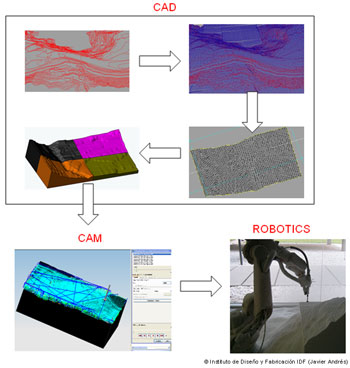
Caso práctico 1: modelo orográfico (E 1:75) del embalse de Arenós (Castellón, España)
El diseño se realiza por medio del módulo Cad de NX y es el punto de partida para la aplicación del resto de las tecnologías asistidas por computador. Por tanto, la calidad del modelo determina fuertemente los resultados que pueden obtenerse en los siguientes pasos del proceso de fabricación. Por ello, se hizo necesario el tratamiento de la información importada desde programas empleados en el ámbito de la topografía (Autocad, MDT v4, Autodesk) (Fig. 2).
Dada la geometría de las piezas que conforman el modelo y la geometría de la herramienta, se realizó en tres ejes tanto el desbaste como el acabado. La figura 3 muestra diferentes secuencias del proceso, así como el modelo finalmente obtenido. Éste, se obtuvo ensamblando cada una de las piezas mecanizadas hasta completar el modelo de 8x13 metros actualmente ubicado en el Departamento de Ingeniería Hidráulica y Medio Ambiente de la Universidad Politécnica de Valencia.

Caso práctico 2: Incorporación de la robótica a sectores tradicionales (Artistas Falleros, Valencia)
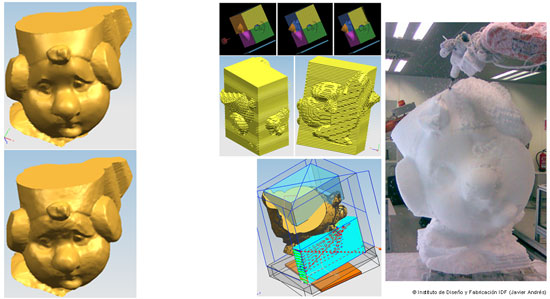
El fichero original es un.stl, tipo de fichero estándar de programas de escaneado, a escala E 1:12. Esto es debido a que los modelos son realizados a pequeña escala por técnicas tradicionales para su posterior reescalado. Se realiza un suavizado de las regiones amplias de manera que la superficie final sea más lisa (Fig. 4). Este suavizado se realiza mediante la herramienta que NX dispone para el tratamiento de cuerpos faceteados y la elección de cada una de las regiones se realiza manualmente.
Análisis del proceso
En cuanto al control del robot, la cabina de control Kuka KRC2 contiene todos los componentes y funciones requeridas para operar el robot, incluyendo el ordenador y fuentes de alimentación. Dicho ordenador realiza las funciones de control, es decir:
- Creación, corrección y archivo de programas
- Diagnosis y asistencia en el arranque
- Secuencias y bucles de control
- Planificación de trayectorias
- Vigilancia del proceso
- Seguridades
- Comunicación con periféricos externos
El principal problema en la adaptación de manipuladores industriales para operaciones de mecanizado reside en la memoria disponible en el control. Los programas KRL deben ser copiados y cargados en una carpeta de programas en una unidad virtual que se ubica en el control (KRC:R1Program) para ser compilados y ejecutados, pero con un tamaño máximo de 3Mb que fácilmente es sobrepasado en piezas complejas. Para evitar esta limitación, se diseña un programa KRL genérico y común a todas las piezas que carga los puntos almacenados en un fichero externo a modo de buffer.
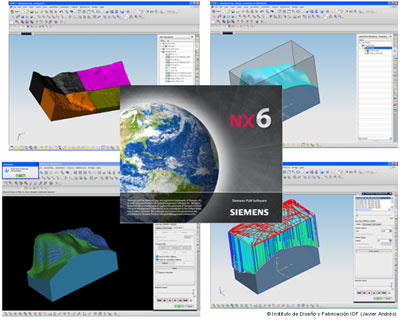
Si nos fijamos en el postprocesamiento, el módulo NX-Cam tiene una serie de peculiaridades. NX (Siemens) es una plataforma informática ideada para el desarrollo digital de productos, con una gama integrada, completa y asociada de aplicaciones Cad/Cam/Cae. De este modo, NX aborda todo el rango de desarrollo de procesos en diseño de producto, manufactura y simulación.
Una vez la trayectoria de la herramienta ha sido generada, NX almacena esta información como una sucesión de eventos y unas variables asociadas. Un evento de trayectoria puede ser una línea, un círculo, un movimiento rápido y, en definitiva, cualquier tarea que suponga una cierta acción en el robot. Las variables asociadas guardan la información del evento (radios, puntos representativos, amplitudes, etc.). Después de esto, el modulo de Cam tiene la posibilidad de programar el tratamiento adecuado de estas variables y de darles el formato en que la información salida es requerida por la maquina herramienta. Esto lo que tradicionalmente es el postprocesamiento.
En ambos casos de estudio, el punto de partida del módulo Cam de NX consiste en una serie de datos, además del diseño de la pieza, como son las condiciones de mecanizado, material de la pieza, tipos de herramienta, profundidades de pasada o el tipo de estrategias de corte. Como es mandatario en todos los procesos de mecanizado, todos los datos generados por el Cam refieren a la posición y orientación del TCP de la herramienta que da lugar al acabado superficial deseado.
Dicha información no refiere a ninguna máquina herramienta específica o articulaciones de robot, sino que el código generado (Cutter Location Source File, CLSF) necesita ser traducido al lenguaje del controlador del sistema de producción que se vaya a emplear. En este caso, una vez se ha generado este código, se mantiene en la memoria del ordenador con sus parámetros asociados para su posterior adaptación al control Kuka KRC2. Esto se conoce como postprocesamiento.
La configurabilidad del postprocesador de NX orientado a KRL (Kuka Robot Languaje) se consigue por medio de la interacción de NX con dos programas en lenguaje TCL (Tool Command Languaje). Uno de ellos trata y adapta el Cam a las particularidades de la célula robotizada con grados de movimiento redundantes (Event Handler) y el otro proporciona el formato de salida adecuado (Definition File).
Problemática asociada al postprocesamiento en células redundantes
El empleo en la industria del mecanizado de sistemas robotizados cada vez mas complejos conlleva dos retos para la integración de las plataformas Cam (Computer Aided Manufacturing) hacia los robots:
- Por un lado, es necesario llevar la información de posicionamiento de la herramienta en un lenguaje entendible por la unidad de control de manipulador (tradicionalmente conocido como postprocesamiento en máquinas herramienta convencionales).
- Adicionalmente, las posibles traducciones hacia el controlador del manipulador en orden a la ejecución de una determinada tarea son infinitas, es decir, aparece el reto optimizar el empleo de los ejes adicionales.
La mayor dificultad para postprocesar una trayectoria de mecanizado generada por un software Cam hacia una célula robotizada compleja estriba en el tratamiento a dar a las articulaciones redundantes para evitar singularidades o limites de rango, con el objetivo último de alcanzar las sucesivas posiciones de la herramienta en el espacio cartesiano siguiendo un criterio de precisión y economía en el movimiento del manipulador. Esto supone dos tareas diferenciadas atendiendo al posicionamiento de la herramienta o al posicionamiento del manipulador:
- Traducción de la información de posicionamiento de la herramienta, generada por el Cam, de acuerdo con los requerimientos del lenguaje del robot.
- Análisis cinemático inverso de la célula para un cierto requerimiento de posicionamiento de la herramienta de corte, con objeto de incluir el tratamiento del posicionamiento del manipulador con ejes adicionales.
Muchos fabricantes de robots industriales resuelven parcialmente el problema por medio de simuladores gráficos como paso intermedio entre la plataforma Cam y la ejecución en el robot. En la práctica, la experiencia del operario a cargo de la célula permite llevar a cabo un control eficiente del movimiento en estas situaciones. Éste, en base a su experiencia, fija el valor de las articulaciones adicionales para determinados apartados del programa, y verifica los movimientos del robot en el seguimiento de la trayectoria. De esta manera, mediante simulación, puede conocer si se alcanza algún límite de rango o configuración singular en cualquier punto. Sin embargo, es una labor tediosa.
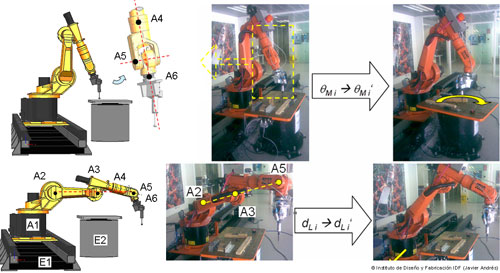
En la figura 6 se aprecian dos configuraciones singulares que conciernen a los trabajos de mecanizado sobre la mesa giratoria, así como dos soluciones prácticas para evitar la singularidad de brazo extendido (por medio de un desplazamiento predominante en el eje lineal) y la singularidad de muñeca (por medio de un giro en la mesa). Estas soluciones prácticas, propias de la lógica borrosa con que trabaja la mente humana y alejadas del análisis y modelado matemático puro, han demostrado su eficiencia y bajo coste computacional (inmediatez) a la hora de resolver problemas de posicionamiento. Por ello, con este razonamiento queda patente y justificada la búsqueda de metodologías rápidas y robustas que emulen el razonamiento del cerebro humano. Éste son las bases del control difuso o fuzzy control.
La configurabilidad del postprocesador integrado en NX mediante el lenguaje TCL antes comentada, permite conectar de manera flexible un cierto numero de módulos en otros lenguajes de programación como C++. Dichos módulos perfectamente puedes ser los encargados de tomar las pertinentes decisiones como lo haría un operario experto. Actualmente ésta es una de las líneas de investigación seguidas en el IDF (UPV). A continuación se trazan las líneas en que se basa el estudio.
Lenguaje Kuka para programación del movimiento: KRL
El controlador KRC-2 de Kuka ofrece comandos específicos de KRL para seguimiento de trayectorias en el espacio cartesiano (comandos de continuous path, CP) en este tipo de manipuladores industriales. Con ellos se controla la velocidad del TCP de la herramienta tal y como es mandatario en cualquier proceso de mecanizado. La estructura de datos requeridos para el posicionamiento de la herramienta de corte en los puntos de la trayectoria sigue la sintaxis:
{E6POS: X, Y, Z, A, B, C, E1, E2}
en la que las coordenadas de posición y orientación del TCP {X, Y, Z, A, B, C} están referidas al sistema de coordenadas cartesiano de la base {B} situado sobre la mesa giratoria. E1 y E2 establecen los valores de articulación del eje lineal y de la mesa giratoria, respectivamente.
A efectos prácticos y según se ha expuesto anteriormente, los datos llevados al controlador del manipulador se refieren al posicionamiento en el espacio cartesiano del manipulador {X, Y, Z, A, B, C} mientras que las articulaciones externas E1 y E2 únicamente son modificadas por el operario en caso de evitación de singularidades o límites de rango en el movimiento de la cadena A1-A6. Este criterio de trabajo atiende a razones de precisión en las tareas y economía en los movimientos articulares.
Programación de la cinemática inversa
En la práctica, las especificaciones de la trayectoria de mecanizado se van a definir en el espacio Cartesiano (posición y orientación de la herramienta de corte) mientras que los controladores del robot trabajan en el espacio de articulaciones (esto es, los valores de cada articulación). Para el postprocesador diseñado, se programa un módulo que calcula los valores de articulación para alcanzar una cierta posición y orientación con el efector final. Este cálculo, denominado cálculo cinemático inverso, es fácilmente resoluble por medio de métodos geométricos, teniendo especial atención en las transformaciones entre los diferentes sistemas de coordenadas {B} y {R} y considerando los límites de rango del manipulador real. Para dicha resolución se recurre a dos observaciones:
- Por un lado, las tres primeras articulaciones de un manipulador se mueven en un plano vertical que permite su resolución por trigonometría. Estas articulaciones definen el denominado posicionamiento grueso.
- Por otro lado, las tres últimas articulaciones se cortan en un punto denominado muñeca (W), y los valores de ángulo se pueden obtener por medio de una secuencia de rotaciones de Euler ZYZ. Éstas articulaciones definene el posicionamiento fino de la herramienta sobre la pieza.
Además, en este caso particular, para esta resolución se parte del conocimiento previo de los valores de articulación de la mesa y el track lineal, de lo contrario el sistema tendría infinitas soluciones posibles para un mismo posicionamiento de la herramienta sobre la pieza a mecanizar.
Control fuzzy de los ejes adicionales
Este controlador está siendo desarrollado mediante Matlab (The MathWorks, Inc.) por medio del Fuzzy Logic Toolbox.
El punto de partida para todos los procesos de mecanizado es una posición conocida de la célula (Home), que es previa y común a todas las ejecuciones que se llevan a cabo en la misma. Como se ha adelantado, es provechoso almacenar los valores de posición previos para minimizar el desplazamiento de las articulaciones adicionales E1 y E2. De este modo es factible aplicar la resolución geométrica de la cinemática inversa previamente programada, para llevar las sucesivas coordenadas de trayectoria al espacio de articulaciones en donde se toman las decisiones de las acciones a realizar.
El siguiente paso consiste en evaluar y decidir si la posición actual de los ejes E1 y E2 es conveniente para el seguimiento del mecanizado o si, por el contrario, es preferible relocalizar el manipulador (por medio del eje lineal) o la pieza (por medio de la mesa giratoria). Desde esta posición, y dependiendo del punto en el espacio de trabajo cartesiano al que deba acudir el TCP de la herramienta, el posicionamiento de los ejes externos es reconsiderado por medio del control fuzzy.
Necesariamente, la experiencia del operario a cargo de la célula es considerada en el diseño del núcleo central del controlador fuzzy. Con esta información se conforma el conjunto de reglas (base de reglas), frente a las cuales el controlador adopta los criterios de decisión para el reposicionamiento del manipulador.
El controlador fuzzy es implementado mediante el Fuzzy Logic Toolbox de Matlab. Éste genera un fichero en el que se guarda la descripción del controlador fuzzy. Dos ficheros en C++ contienen el código necesario para implementar un motor de inferencia fuzzy independiente de Matlab que lee las características de dicho fichero, sin necesidad de ejecutar Matlab.
Simulación gráfica
Una vez que se tiene un controlador fuzzy que resuelve la redundancia cinemática que posee la célula robotizada, y como paso previo a la ejecución real se hace necesario verificar la trayectoria obtenida para salvaguardar la integridad de la célula como de los útiles.
Para la verificación de la trayectoria obtenida se ha optado por utilizar el modulo de simulación de movimientos del que dispone NX llamado Motion, consiguiendo que todo el desarrollo se encuentre dentro de la misma aplicación.
Motion de NX es un módulo mediante el cual se pueden simular tanto la cinemática como de dinámica de mecanismos complejos, con es el caso que nos ocupa de la célula robotizada. Mediante este simulador se puede detectar las posibles colisiones del robot con el entorno y autocolisiones (colisiones con el propio robot) que no son tenidas en cuenta a la hora de generar las trayectorias de mecanizado.
Este simulador tiene como entrada los valores de articulación en cada instante, lo cual hace que no necesite un resolvedor propio de indeterminaciones. Además se pueden verificar los pares generados en las articulaciones, gracias al cálculo dinámico que son un estimador de la precisión en el movimiento. En la figura 7 se puede ver una imagen de la simulación de la célula robotizada.































