Segmentación automática de imágenes de cultivos: estudio comparativo de modelos de color

El problema de la segmentación automática suelo/plata ha sido ampliamente estudiado por diversos investigadores, como puede comprobarse en dos revisiones recientes del estado del arte (Lin et al., 2013; McCarthy et at., 2010). En la mayoría de estos trabajos la clasificación se hace usando diversas técnicas como umbralización, discriminantes lineales, modelos de gausianos, lógica difusa, redes neuronales, y otros; pero el espacio de color es fijado de antemano, y se echan en falta estudios comparativos sobre la efectividad de diversos modelos de color en plantas. Sin embargo es habitual encontrar ese tipo de trabajos comparativos otros dominios. Por ejemplo, Shih y Lui (2012) evaluaron comparativamente 12 espacios de color en aplicaciones de procesamientos de caras, y llegaron a la conclusión de que los espacios óptimos son YUV y YIQ; Luszczkiewicz-Piatek (2014) estudia la elección del espacio de color para la recuperación de imágenes en grandes bases de datos; el color se representa con modelos de mezcla de gaussianas y se analizan 11 espacios de color. Por su parte, Terrillon y Akamatsu (2000) introdujeron el espacio TSL, y se compararon 9 espacios en la detección de caras.

En consecuencia, el objetivo de este trabajo es realizar un estudio completo y exhaustivo, con el propósito de seleccionar el espacio de color óptimo y la forma más efectiva de representar las distribuciones de color para los problemas de clasificación en el dominio agromótico, y en concreto para la segmentación automática de plantas en imágenes.

Imágenes utilizadas para la experimentación

Clasificación y representación del color

El color concreto de un píxel del suelo, o de las plantas, puede entenderse como un suceso estocástico dentro del espacio n-dimensional definido por el espacio de color usado. En el caso del suelo, la distribución de probabilidad del color está determinada por el tipo y composición del suelo, la iluminación en el momento de tomar la foto y los parámetros propios de la cámara, como el balance de blancos; de forma similar ocurre con el color de la cobertura vegetal, donde la clorofila da lugar a la predominancia de los tonos verdes.

Supongamos conocidas las funciones de distribución probabilidad del color del suelo, p_suelo(color), y del color de la planta, p_planta (color), donde color es una tupla de un espacio de color cualquiera. Considerando equiprobables las probabilidades a priori de suelo y de planta, la probabilidad de que un píxel, color, concreto sea de planta o de suelo, puede calcularse de forma sencilla mediante la regla de Bayes, dada por la fórmula:

En consecuencia, el píxel concreto es asignado a la clase de mayor probabilidad entre P(planta|color) y P(suelo|color). De manera trivial, el problema se reduce a buscar el máximo entre p_planta(color) y p_suelo(color) para cada píxel de las imágenes.

La clasificación píxel-a-píxel obtenida de esta forma se puede mejorar con la aplicación de operaciones de procesamiento local, que tienen en cuenta la vecindad de los píxeles. En concreto, se han comprobado dos opciones: reducción de la imagen por 2 usando interpolación de supermuestreo, y operaciones de morfología matemática. Mientras que la primera consigue reducir el nivel de ruido de las imágenes (al hacer un promediado de píxeles), la segunda permite limpiar el resultado de valores espurios. Además, ambas operaciones pueden aplicarse de forma combinada.

Espacios de color analizados

Las formas que adoptan las funciones de distribución de probabilidad, p_suelo y p_planta, dependen, lógicamente, del espacio de color adoptado. Cada espacio genera distintos grados de separación entre las distribuciones, afectando así la efectividad de la clasificación. Los modelos de color seleccionados para el estudio, escogidos entre los más habituales en aplicaciones de visión artificial (Luszczkiewicz, 2014), son los siguientes:

• RGB, rgb. El espacio RGB es el más extendido en dispositivos de captura y generación de color. Se basa en un modelo de mezcla aditivo, donde cada color se forma por combinación de los tres colores primarios: rojo (R), verde (G), y azul (B). A partir de este modelo se define la variante normalizada rgb, que consiste en dividir los valores de RGB por (R+G+B).
• XYZ. Es un modelo que simula la respuesta de los tres tipos de fotorreceptores de la retina (aquellos con espectros de absorción en longitudes de ondas altas, medias y bajas). La forma concreta de estos espectros de absorción fue definida por la CIE (Commission internationale de l'éclairage) en 1931.
• HSV, HLS. En estos modelos el color se descompone en términos fácilmente interpretables como la intensidad (V, L), la saturación o pureza (S), y el matiz de color (H). Son modelos muy habituales en análisis y generación gráfica.
• YCrCb, YUV. Se trata de modelos orientados a compresión y trasmisión de imágenes. Se basan en la separación de un canal Y de luminancia (o intensidad luminosa), y dos canales de crominancia (o tono del color, independiente de su luminosidad). Los canales Cr y Cb corresponden, en esencia, a los canales R y B normalizados en intensidad, respectivamente.
• L*a*b*, L*u*v*. Estos modelos fueron definidos por la CIE para aplicaciones industriales del color. De forma similar a los anteriores, separan un canal de luminosidad (en este caso L*) y dos canales de crominancia (a*-b* y u*-v*). Estos últimos se definen mediante transformaciones no lineales del modelo RGB, con el fin de conseguir representaciones perceptualmente uniformes del color.
• TSL, I1I2I3. Algunos modelos han sido diseñados específicamente para ciertas aplicaciones. Por ejemplo, el modelo TSL fue creado para abordar problemas de detección de piel humana (Terrillon y Akamatsu, 2000). Por otro lado, I1I2I3 se propuso para la segmentación de color, como una decorrelación de los componentes RGB usando la transformada Karhunen-Loeve.

Representación de las distribuciones de probabilidad de color

A su vez, existen distintas alternativas en la representación de los histogramas. En primer lugar, el número de canales a utilizar, puesto que no todos los canales son igual de útiles para el problema. Como veremos, descartar algunos canales puede producir mejores resultados que usarlos todos. En segundo lugar, tenemos el tamaño del histograma. Los histogramas suponen una discretización del rango de las variables estudiadas. La discretización se hace en potencias de 2, lo que permite obtener una distribución uniforme de los valores de entrada, representados con bytes. En definitiva, para cada uno de los espacios de color, tenemos la opción de usar histogramas de un canal, dos canales o tres canales, con 16, 32, 64, 128 o 256 celdas por dimensión.

Como segundo experimento se ha realizado una clasificación automática de las imágenes de la segunda secuencia (un total de 61 imágenes), comparando el resultado con la clasificación manual de los expertos. El valor obtenido en este caso es el porcentaje de acierto final a nivel de píxel para cada opción.

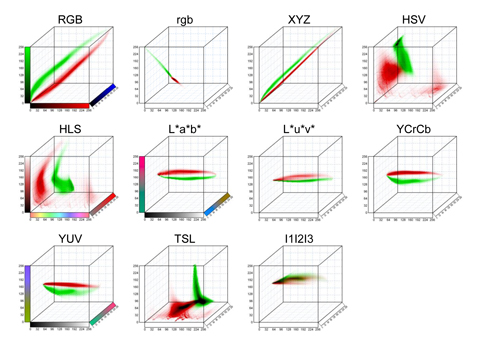
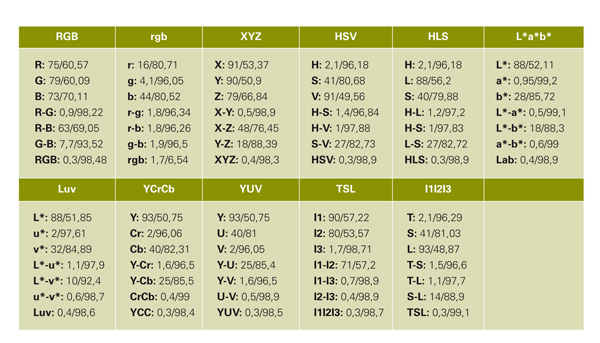
Solapamiento entre distribuciones y acierto de clasificación

Podemos destacar algunos hechos relevantes. Como era de esperar, el solapamiento disminuye con el número de canales y con el tamaño de los histogramas. Sin embargo, mientras que en el primer factor las reducciones son muy significativas, en el segundo no alcanzan el 30% de reducción en los mejores casos. Además, tamaños grandes de histogramas aumentan el riesgo de 'sobreajuste' a los datos de entrenamiento.

El canal que por sí solo consiguen mejores resultados es el a* del L*a*b*, con solo un 0,95% de solapamiento y un 99,2% de acierto. El mejor resultado se obtiene para 32 celdas, aunque los resultados son también muy buenos para 64 y 128. Las siguientes opciones, a más distancia, son canales I3 en I1I2I3, Cr en YCrCb, V en YUV, u* en L*u*v*, H en HSV/HLS, y T en TSL, con precisiones siempre superiores al 96%. Por su parte, ninguno de los canales de RGB es capaz por sí solo de conseguir un solapamiento bajo, como tampoco los canales de luminosidad de los distintos espacios.

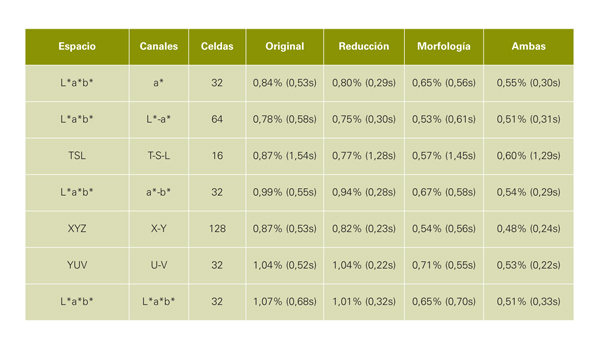
Finalmente, se han seleccionado algunas de las configuraciones que producen mejores resultados y sobre ellas se han aplicado las mejoras adicionales antes descritas: reducción por 2 de las imágenes; aplicación de morfología matemática; y la combinación de ambas. En la figura 3 se pueden ver algunos ejemplos de segmentación automática incluyendo estas mejoras. Los resultados completos pueden verse en la tabla 2, que muestra también los tiempos de ejecución en un ordenador medio.

De este estudio podemos concluir varios hechos. Primero, que la clasificación por color resulta viable en la práctica al producir unos resultados del 99,5% de acierto en la clasificación, requiriendo únicamente 0,3 segundos por imagen en un ordenador estándar. Segundo, que los mejores modelos de color son aquellos que separan un canal de luminancia y dos de crominancia, donde los segundos son los que aportan la información relevante para el problema. En concreto, el espacio L*a*b* ha demostrado estar por encima del resto en la mayoría de los casos; el espacio RGB, a pesar de ser uno de los más extendidos, no debería ser usado para la clasificación automática. Finalmente, la aplicación de operaciones de pre- (reducción de las imágenes con supermuestreo) y post-procesamiento (operadores de morfología matemática) es muy útil para mejorar los resultados y reducir los tiempos de ejecución. Actualmente, el equipo de investigación está trabajando en la implementación de aplicaciones a nivel de usuario para realizar la segmentación automática en dispositivos móviles, usando los resultados de este estudio.

Referencias bibliográficas

• Allen, R.G., Pereira, L.S., Raes, D., Smith, M. 1998. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. FAO, Rome 300, 6541.
• Cubero, S., Aleixos, N., Moltó, E., Gómez-Sanchis, J., Blasco. J. 2011. Advances in machine vision applications for automatic inspection and quality evaluation of fruits and vegetables. Food and Bioprocess Technology, Vol. 4 (4):487-504.
• Fernández-Pacheco, D.G., Escarabajal-Henarejos, D., Ruiz-Canales, A., Conesa, J., Molina-Martínez, J.M. 2014. A new digital image processing based methodology for determining Kc in lettuce crops in the Southeast of Spain. Biosystems Engineering 117:23-34.
• Kumar, P., Sengupta, K., Lee, A. 2002. A comparative study of different color spaces for foreground and shadow detection for traffic monitoring system. Intelligent Transportation Systems:100-105.
• Lin, K., Chen, J., Si, H., Junhui, W. 2013. A review on computer vision technologies applied in greenhouse plant stress detection. Advances in Image and Graphics Technologies, 363, 192–200.
• Luszczkiewicz-Piatek, M. 2014. Which color space should be chosen for robust color image retrieval based on mixture modeling. Advances in Intelligent Systems and Computing. Vol. 233:55-64.
• McCarthy, C.L., Cheryl, N.H., Hancock, S.R. 2010 Applied machine vision of plants - a review with implications for field deployment in automated farming operations. Intelligent Service Robotics, 3 (4), 209–217.
• Shih, P., Liu, C. 2005. Comparative assessment of content-based face image retrieval in different color spaces. Int. J. Patt. Recogn. Artif. Intell. 19(7), 873-893.
• Terrillon, J.C., Akamatsu, S. 2000. Comparative performance of different chrominance spaces for color segmentation and detection of human faces in complex scene images. International Conf. on Face and Gesture Recognition, 54-61.